4.4用尺规作三角形
- 格式:doc
- 大小:374.00 KB
- 文档页数:1



全新修订版教学设计
(教案)
七年级数学下册
老师的必备资料
家长的帮教助手
学生的课堂再现
北师大版
4.4 用尺规作三角形
1.已知两边及其夹角会作三角形;(重点,难点)
2.已知两角及其夹边会作三角形.(重点,难点)
3.已知三边会作三角形.(重点,难点)
一、情境导入
小明在一个工程施工图上看到一个三角形,他想用直尺和圆规画一个与这个三角形全等
的三角形,应当怎样画?
二、合作探究
探究点:用尺规作三角形
【类型一】已知两边及其夹角作三角形
如图,已知∠α和线段m,n.求作△ABC,使∠B=∠α,BA=n,BC=m.
解:作法:1.作∠MBN=α;
2.在射线BN,BM上分别截取BC=m,BA=n;
3.连接AC,则△ABC就是所求作的三角形.
方法总结:已知两边及其夹角作三角形的理论依据是判定三角形全等的“SAS”,作图时可先作一个角等于已知角,再在角的两边分别截取已知线段长即可.变式训练:见《学。

用尺规作三角形〖教学目标〗1.知识与技能:掌握利用尺规作三角形的根本方法。
2.过程与方法:(1)经历在给定条件下(两角夹边、两边夹角和三边),利用尺规作出三角形的过程;(2)能结合三角形全等的条件与同伴交流作图过程和结果的合理性。
3.情感与态度:在利用尺规作图的过程中,培养自信心、动手能力和探索精神。
〖教学设计〗(一)巧设现实情境,引入新课师:在第二章我们已学习过用尺规作一条线段等于线段,作一个角等于角。
现在回忆一下用尺规作图的一般步骤。
生:用尺规作图的步骤有:、求作。
师:他的答复对吗?生:他的答复不完整,应该还有分析、作法。
(点评:让学生在倾听其他同学发言的过程中,培养学生的批判意识和疑心精神。
)师:很好。
下面大家来作一条线段等于线段。
生:(小组讨论后一位同学答复):线段a。
求作:一条线段,使它等于a。
图1作法:(1)作射线AC;(2)在射线AC上截取AB=a。
那么线段AB就是所求作的线段。
图2(点评:教师让学生分组讨论,有意识地培养他们合作学习的能力。
)师:好,那如何作一个角等于角呢?生::∠AOB。
求作:一个角,使它等于∠AOB。
图3作法:(1)作射线O′A′;(2)以O为圆心,以任意长为半径画弧,交OA于点C,交OB于点D;(3)以O′为圆心,以OC的长为半径画弧,交O′A′于点C′;(4)以点C′为圆心,以CD的长为半径画弧,交前弧于点D′;(5)过D′作射线O′B′。
那么∠A′O′B′就是所求作的角。
图4师:很好,大家根本掌握了用尺规作线段和角。
边和角是三角形的根本元素,如果给了一些三角形的根本元素,你能用尺规作出一个三角形,使它满足条件吗?这节课我们就利用尺规作一个三角形与三角形全等。
(二)讲授新课师:下面我们来做一做:三角形的两边及其夹角,求作这个三角形。
如何求作这个图形呢?(师生共析:需要先写出、求作,然后进展分析,最后作图形,写作法。
) :线段a,c,∠α。
图5 求作:△ABC,使BC=a,AB=c,∠ABC=∠α。
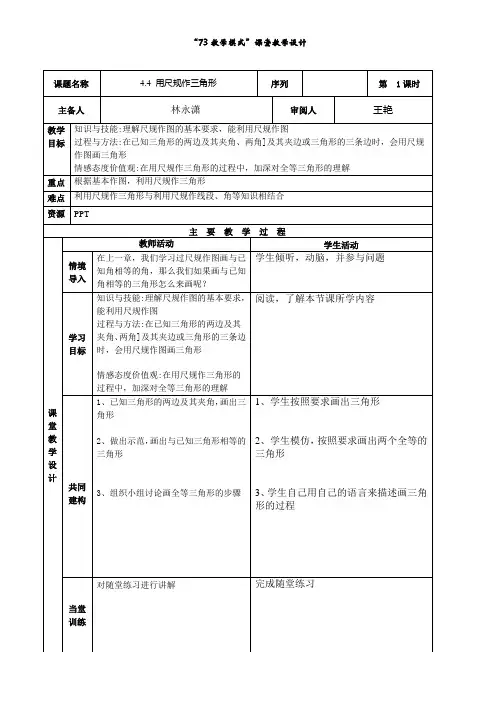
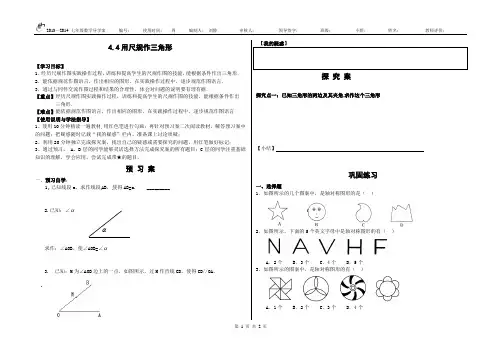
4.4用尺规作三角形【学习目标】1.经历尺规作图实践操作过程,训练和提高学生的尺规作图的技能,能根据条件作出三角形.2.能依据规范作图语言,作出相应的图形,在实践操作过程中,逐步规范作图语言.3.通过与同伴交流作图过程和结果的合理性,体会对问题的说明要有理有据.【重点】经历尺规作图实践操作过程,训练和提高学生的尺规作图的技能,能根据条件作出三角形.【难点】能依据规范作图语言,作出相应的图形,在实践操作过程中,逐步规范作图语言【使用说明与学法指导】1、使用10分钟精读一遍教材,用红色笔进行勾画;再针对预习案二次阅读教材,解答预习案中的问题;把疑惑随时记载“我的疑惑”栏内,准备课上讨论质疑;2、利用20分钟独立完成探究案,找出自己的疑惑或需要探究的问题,用红笔做好标记;3、通过预习, A、B层的同学能够灵活选择方法完成探究案的所有题目;C层的同学注重基础知识的理解,学会应用,尝试完成带★的题目。
预习案一、预习自学:1.已知线段a,求作线段AB,使得AB=a. _________2.已知:∠α求作:∠AOB,使∠AOB=∠α3. 已知:M为∠AOB边上的一点,如图所示,过M作直线CD,使得CD//OA。
【我的疑惑】探究案探究点一:已知三角形的两边及其夹角,求作这个三角形【小结】巩固练习一、选择题1.如图所示的几个图案中,是轴对称图形的是()2.如图所示,下面的5个英文字母中是轴对称图形的有()A.2个 B.3个 C.4个 D.5个3.如图所示的图案中,是轴对称图形的有()A.1个 B.2个 C.3个 D.4个α4.你认识世界上各国的国旗吗?如图7-4所示,观察下面的一些国家的国旗,是轴对称图形的有( )A .甲乙丙丁戊B .甲乙丁戊C .甲乙丙戊D .甲乙戊 二、填空题5.下面图形是轴对称图形的有A .角B .线段C .太极图D .香港特别行政区区旗上的紫荆花E .等腰三角形 F .五角星6.一天, 小明, 小刚, 小强, 小军四个人发生了争论: 小明认为:凡是有两条边相等的三角形都 是轴对称图形; 小刚认为:等腰直角三角形不是轴对称图形;小强认为:有一个角等于45˚的直角三角形是轴对称图形;小军认为:有一个角是30˚, 另一个角为120˚的三角形是轴对称图形. 你知道他们谁说的不对吗?三、解答题7.在如图所示的轴对称图形中,用虚线画出它们所有的对称轴.8.如图所示,以虚线为对称轴画出图形的另一半.9.★ △ABC 中,∠C=90˚, ∠A 大小可以变化,现将△ABC 沿一边翻转一次,使翻转后的图形与原图形所构成的新图形的各边都相等,求出∠A 的度数,并说明该如何翻转?【课堂小结】数学知识方面数学方法方面。

4.4 用尺规作三角形1.已知两边及其夹角会作三角形;(重点,难点)2.已知两角及其夹边会作三角形.(重点,难点)3.已知三边会作三角形.(重点,难点)一、情境导入小明在一个工程施工图上看到一个三角形,他想用直尺和圆规画一个与这个三角形全等的三角形,应当怎样画?二、合作探究探究点:用尺规作三角形【类型一】已知两边及其夹角作三角形如图,已知∠α和线段m,n.求作△ABC,使∠B=∠α,BA=n,BC=m.解:作法:1.作∠MBN=α;2.在射线BN,BM上分别截取BC=m,BA=n;3.连接AC,则△ABC就是所求作的三角形.方法总结:已知两边及其夹角作三角形的理论依据是判定三角形全等的“SAS”,作图时可先作一个角等于已知角,再在角的两边分别截取已知线段长即可.【类型二】已知两角及其夹边作三角形已知∠α,∠β,线段c.求作△ABC,使得∠ABC=∠α,∠ACB=∠β,BC=c.解:作法:1.作线段BC=c;2.在BC的同旁,作∠DBC=∠α,作∠ECB=∠β,DB与EC交于点A.则△ABC就是所求作的三角形.方法总结:已知两角及其夹边作三角形的理论依据是判定三角形全等的“ASA”,作图时可先作一条边等于已知边,再在这条边的同侧,以边的两个端点为顶点作两个角分别等于已知角即可.【类型三】已知三边作三角形已知三条线段a、b、c,用尺规作出△ABC,使BC=a,AC=b、AB=c.解:作法:1.作线段BC=a;2.以点C为圆心,以b为半径画弧,再以B为圆心,以c为半径画弧,两弧相交于点A;3.连接AC和AB,则△ABC即为所求作的三角形,如图所示.方法总结:已知三角形三边的长,根据全等三角形的判定“SSS”,知三角形的形状和大小也就确定了.作三角形相当于确定三角形三个顶点的位置.因此可先确定三角形的一条边(即两个顶点),再分别以这条边的两个端点为圆心,以已知线段长为半径画弧,两弧的交点即为另一个顶点.三、板书设计1.已知两边及其夹角作三角形2.已知两角及其夹边作三角形3.已知三边作三角形本节课学习了有关三角形的作图,主要包括两种基本作图:作一条线段等于已知线段,作一个角等于已知角.作图时,鼓励学生一边作图,一边用几何语言叙述作法,培养学生的动手能力、语言表达能力。




4.4 用尺规作三角形1.已知线段a,b和∠α,求作△ABC,使其有一个内角等于∠α,且∠α的对边等于a,另有一边等于b.2.已知线段a,h,如图所示,求作等腰三角形ABC,使得底边BC=a,BC边上的高为h(保留作图痕迹,不写作法).3.已知一个三角形的两边分别为线段a,b,并且边a上的中线为线段c,求作此三角形(要求:用尺规作图,写出已知、求作,保留作图痕迹,不写作法,要写结论).已知:求作:结论:4.如图,已知a和∠α,用尺规作一个三角形ABC,使AB=AC=2a,∠BAC=180°-∠α.【知识要点】1.作三角形:按所给的已知条件,依据三角形全等的判定方法作符合要求的三角形.2.作三角形主要结合以下几种已知条件:(1)知两边及其夹角,求作三角形;(2)已知两角及其夹边,求作三角形;(3)已知两角及一角的对边,求作三角形;(4)已知三边,求作三角形.【温馨提示】求作三角形的过程用到了两种最基本的尺规作图法,一种是作一个角等于已知角;另一种是作一条线段等于已知线段.因此确定求作三角形的作图顺序,应先画出草图,标上已知线段和角,并经过分析得出作图顺序.【方法技巧】作三角形的步骤:先写出已知、求作,然后进行分析,最后画出图形,写出作法.答案:1.解:如图所示.2.解:如图,△ABC为所求作的图形.3.解:已知:线段a,b,c;求作:△ABC,使AC=b,BC=a,D是BC的中点,且AD=c;(或:求作△ABC使AC=b,BC=a,BC边上的中线AD=c)结论:如图,△ABC即为所求.4.解:作法:首先作射线,在射线上截取AB=2a,再作∠BAC=180°-∠α,再截取AC=AB=2a,连接BC即可(图略).。