机械设计 第九版 第10章

第三章 机械零件的强度习题答案3-1某材料的对称循环弯曲疲劳极限MPa 1801=-σ，取循环基数60105⨯=N ，9=m ，试求循环次数N 分别为7 000、25 000、620 000次时的有限寿命弯曲疲劳极限。

[解] MPa 6.373107105180936910111=⨯⨯⨯==--N N σσN MPa 3.324105.2105180946920112=⨯⨯⨯==--N N σσN MPa 0.227102.6105180956930113=⨯⨯⨯==--N N σσN 3-2已知材料的力学性能为MPa 260=s σ，MPa 1701=-σ，2.0=σΦ，试绘制此材料的简化的等寿命寿命曲线。

[解] )170,0('A )0,260(C 012σσσΦσ-=- σΦσσ+=∴-1210 MPa 33.2832.0117021210=+⨯=+=∴-σΦσσ 得)233.283,233.283(D '，即)67.141,67.141(D '根据点)170,0('A ，)0,260(C ，)67.141,67.141(D '按比例绘制该材料的极限应力图如下图所示3-4圆轴轴肩处的尺寸为：D=72mm，d=62mm，r=3mm。

如用题3-2中的材料，设其强度极限σB=420MPa，精车，弯曲，βq=1，试绘制此零件的简化等寿命疲劳曲线。

[解] 因2.14554==dD，067.0453==dr，查附表3-2，插值得88.1=ασ，查附图3-1得78.0≈σq，将所查值代入公式，即()()69.1188.178.0111k=-⨯+=-α+=σσσq查附图3-2，得75.0=σε；按精车加工工艺，查附图3-4，得91.0=σβ，已知1=qβ，则35.211191.0175.069.1111k=⨯⎪⎭⎫⎝⎛-+=⎪⎪⎭⎫⎝⎛-+=qσσσσββεK()()()35.267.141,67.141,0,260,35.2170,0DCA∴根据()()()29.60,67.141,0,260,34.72,0DCA按比例绘出该零件的极限应力线图如下图3-5如题3-4中危险截面上的平均应力MPa20m=σ，应力幅MPa20a=σ，试分别按①C r =②C σ=m ，求出该截面的计算安全系数ca S 。

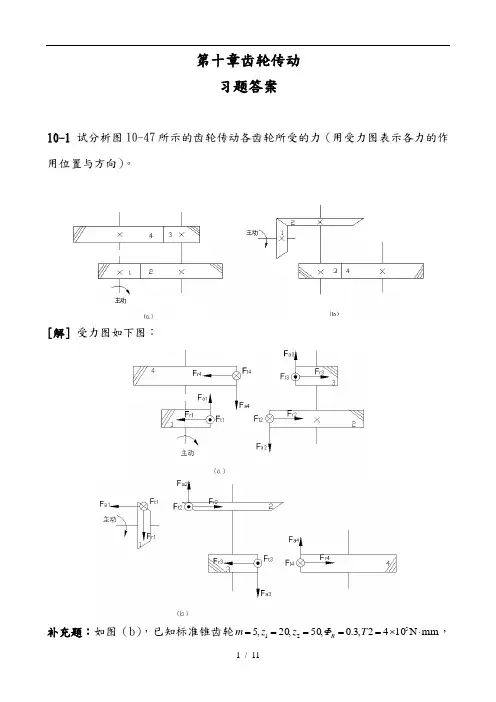
第十章齿轮传动 习题答案10-1 试分析图10-47所示的齿轮传动各齿轮所受的力（用受力图表示各力的作用位置与方向）。

[解] 受力图如下图：补充题：如图（b ），已知标准锥齿轮mm N 1042,3.0,50,20,5521⋅⨯=====T Φz z m R ，标准斜齿轮24,63==z m n ，若中间轴上两齿轮所受轴向力互相抵消，β应为多少？并计算2、3齿轮各分力大小。

[解]（1）齿轮2的轴向力：()222222222sin tan 5.012sin tan 2sin tan δαz Φm T δαdm T δαF F R t a -=== 齿轮3的轴向力：βz m T ββz m T βd T βF F n n t a sin 2tan cos 2tan 2tan 33333333=⎪⎪⎭⎫ ⎝⎛=== 3232,20,T T αF F a a =︒==()βz m T δαz Φm T n R sin 2sin tan 5.01233222=-∴即()2235.01sin tan sin z Φm δαz m βR n -=由5.22050tan 122===z z δ 928.0sin 2=∴δ371.0cos 2=δ ()()2289.0503.05.015928.020tan 2465.01sin tan sin 223=⨯⨯-⨯⨯︒⨯⨯=-=∴z Φm δαz m βR n即︒=231.13β （2）齿轮2所受各力：()() 3.765kN N 10765.3503.05.01510425.01223522222=⨯=⨯⨯-⨯⨯⨯=-==z Φm T dm T F R t0.508kNN 10508.0371.020tan 10765.3cos tan 33222=⨯=⨯︒⨯⨯==δαF F t r kN 272.1N 10272.1928.020tan 10765.3sin tan 33222=⨯=⨯︒⨯⨯==δαF F t akN 420cos 10765.3cos 322=︒⨯==αF F t n齿轮3所受各力：kN 408.5N 10408.5231.13cos 2461042cos 2cos 22353232333=⨯=︒⨯⨯⨯==⎪⎪⎭⎫ ⎝⎛==βz m T βz m T d T F n n tkN 022.2N 10022.2321.12cos 20tan 10408.5cos tan 3333=⨯=︒︒⨯⨯==βαF F n t rkN 272.1N 10272.1321.12cos 20tan 10408.5tan 10408.5tan 33333=⨯=︒︒⨯⨯⨯⨯==βF F t akN 889.5N 10889.5321.12cos 20cos 10765.3cos cos 3333=⨯=︒︒⨯==βαF F n t n10-6设计铣床中的一对圆柱齿轮传动，已知54,26min,r 1450,kW 5.72111====z z n P ，寿命h 12000=h L ，小齿轮相对其轴的支承为不对称布置，并画出大齿轮的机构图。

10-1证明当升角与当量摩擦角符合时，螺纹副具有自锁性。

当时，螺纹副的效率所以具有自锁性的螺纹副用于螺旋传动时，其效率必小于 50%。

10-2解由教材表10-1、表10-2查得，粗牙，螺距，中径螺纹升角，细牙，螺距，中径螺纹升角对于相同公称直径的粗牙螺纹和细牙螺纹中，细牙螺纹的升角较小，更易实现自锁。

10-3解查教材表10-1得粗牙螺距中径小径螺纹升角普通螺纹的牙侧角，螺纹间的摩擦系数当量摩擦角拧紧力矩由公式可得预紧力拉应力查教材表 9-1得 35钢的屈服极限拧紧所产生的拉应力已远远超过了材料的屈服极限，螺栓将损坏。

10-4解（1）升角当量摩擦角工作台稳定上升时的效率：（ 2）稳定上升时加于螺杆上的力矩（ 3）螺杆的转速螺杆的功率（ 4）因，该梯形螺旋副不具有自锁性，欲使工作台在载荷作用下等速下降，需制动装置。

其制动力矩为10-5解查教材表9-1得 Q235的屈服极限，查教材表 10-6得，当控制预紧力时，取安全系数由许用应力查教材表 10-1得的小径由公式得预紧力由题图可知，螺钉个数，取可靠性系数牵曳力10-6解此联接是利用旋转中间零件使两端螺杆受到拉伸 ,故螺杆受到拉扭组合变形。

查教材表 9-1得，拉杆材料Q275的屈服极限，取安全系数，拉杆材料的许用应力所需拉杆最小直径查教材表 10-1，选用螺纹（）。

10-7解查教材表 9-1得，螺栓35钢的屈服极限，查教材表 10-6、10-7得螺栓的许用应力查教材表 10-1得，的小径螺栓所能承受的最大预紧力所需的螺栓预紧拉力则施加于杠杆端部作用力的最大值10-8解在横向工作载荷作用下，螺栓杆与孔壁之间无间隙，螺栓杆和被联接件接触表面受到挤压；在联接接合面处螺栓杆则受剪切。

假设螺栓杆与孔壁表面上的压力分布是均匀的，且这种联接的预紧力很小，可不考虑预紧力和螺纹摩擦力矩的影响。

挤压强度验算公式为：其中；为螺栓杆直径。

螺栓杆的剪切强度验算公式其中表示接合面数，本图中接合面数。

第10章轮系前面我们己经讨论了一对齿轮传动及蜗杆传动的应用和设计问题，然而实际的现代机械传动，运动形式往往很复杂。

由于主动轴与从动轴的距离较远，或要求较大传动比，或要求在传动过程中实现变速和变向等原因，仅用一对齿轮传动或蜗杆传动往往是不够的, 而是需要采用一系列相互啮合的齿轮组成的传动系统将主动轴的运动传给从动轴。

这种由一系列相互啮合的齿轮(包括蜗杆、蜗轮)组成的传动系统称为齿轮系，简称轮系。

本章重点讨论各种类型齿轮系传动比的计算方法，并简要分析各齿轮系的功能和应用。

10.1 轮系的分类组成轮系的齿轮可以是圆柱齿轮、圆锥齿轮或蜗杆蜗轮。

如果全部齿轮的轴线都互相平行，这样的轮系称为平面轮系；如果轮系中各轮的轴线并不都是相互平行的，则称为空间轮系。

再者，通常根据轮系运动时各个齿轮的轴线在空间的位置是否都是固定的，而将轮系分为两大类：定轴轮系和周转轮系。

10.1.1定轴轮系在传动时所有齿轮的回转轴线固定不变的轮系，称为定轴轮系。

定轴轮系是最基本的轮系，应用很广。

由轴线互相平行的圆柱齿轮组成的定轴齿轮系，称为平面定轴轮系，如图10.1所示。

a)b)图10.1 平面定轴齿轮系包含有圆锥齿轮、螺旋齿轮、蜗杆蜗轮等空间齿轮的定轴轮系，称为空间定轴轮系，如图10.2所示。

图10.2 空间定轴轮系10.1.2 周转轮系轮系在运动过程中，若有一个或一个以上的齿轮除绕自身轴线自转外，其轴线又绕另一个齿轮的固定轴线转动，则称为周转轮系，也叫动轴轮系。

如图10.3所示。

a) 周转轮系结构图b)差动轮系c)行星轮系图10.3周转轮系其中齿轮2的轴线不固定，它一方面绕着自身的几何轴线O2旋转，同时O2轴线，又随构件H绕轴线O H公转。

分析周转轮系的结构组成，可知它由下列几种构件所组成：1.行星轮：当轮系运转时，一方面绕着自己的轴线回转(称自转)，另一方面其轴线又绕着另一齿轮的固定轴线回转(称公转)的齿轮称行星轮，如图10.3中的齿轮2。

第10章　齿轮传动一、选择题1．圆柱齿轮传动，当齿轮直径不变，而减小模数时，可以（ ）。

A．提高齿轮的弯曲强度B．提高齿面的接触强度C．改善传动的工作平稳性D．增大齿轮传递的转矩【答案】C【解析】根据公式d＝mz，齿轮的直径不变，减小模数，齿数将增加，重合度增大，从而改善运动的平稳性，还能降低齿高，减小齿坯尺寸，降低加工时的切削量，有利于节省制造费用。

2．直齿圆柱齿轮与斜齿圆柱齿轮相比，其承载能力和运动平稳性（ ）。

A．直齿轮好B．斜齿轮好C．二者都一样D．随使用情况而定【答案】B【解析】与直齿圆柱齿轮相比，斜齿圆柱齿轮啮合传动时，齿面接触线是斜直线，每对齿是逐渐进入啮合又逐渐退出啮合，因此传动更平稳，承载能力更大。

3．一对标准直齿圆柱齿轮传动，已知z1＝20，z2＝60，其齿形系数是（ ）。

A．Y F1＞Y F2B．Y F1＝Y F2C．Y F1＜Y F2D．无法确定【答案】A【解析】标准直齿圆柱齿轮中，齿数越少，齿形系数越大。

4．齿宽系数φd在（ ）情况下可取较小值。

A．齿轮在轴上为悬臂布置B．齿轮在轴上非对称布置于两轴承之间C．齿轮对称布置于刚性轴的两轴承之间D．以上三种情况下取值相同【答案】A【解析】根据齿宽系数选取表可看出，当齿轮在轴上为悬臂布置时，可以选择较小的齿宽系数。

5．为了提高齿根抗弯曲强度，可（ ）。

A．增大模数B．保持分度圆直径不变而增加齿数C．采用负变位齿轮D．保持齿数不变而减小分度圆直径【答案】A【解析】影响齿根弯曲疲劳强度的主要因素是模数，增大模数，弯曲强度提高。

6．为改善或减小齿轮的动载荷系数，可（ ）。

A．将齿轮加工成鼓形齿B．将两齿轮做成变位齿轮C．将一个齿轮的轮齿齿顶及齿根都进行修缘D．对轮齿进行螺旋角修形【答案】C【解析】修缘之后的轮齿在开始啮合阶段相啮合的轮齿的法节差减小，从而产生的动载荷减小，故可以通过修缘减小动载荷系数。

7．某场运输带由速度1440r/min的电动机通过三套减速装置来驱动，其中a．双级直齿圆柱齿轮减速器b．套筒滚子链传动c．三角带传动。

第十章 联接
10-1 螺纹的主要类型有哪几种？
[解] 类型：矩形螺纹、三角螺纹（普通）、梯形螺纹和锯齿螺纹。

10-2 螺纹联接的种类有哪些？
[解] 类型：螺栓联接、双头螺柱联接、螺钉联接和紧定螺钉连接。

10-3螺纹的主要参数有哪几种？
[解] 螺纹的主要参数：（1）大径d （D ）；（2）小径d 1（D 1）；（3）中径d 2(D 2)；（4）螺距p ；
(5)导程s ；（6）螺纹升角；（7）牙型；（8）牙型斜角；（9）螺纹牙的工作高度h 。

螺距和导程的关系： s=np ； 单线时相等。

10-4 螺纹联接常用的防松方法有哪几种？它们防松的原理是怎么样的？
[解] 防松方法：摩擦防松、机械防松、破坏纹副的防松。

防松原理都是防止螺旋副相对转
动。

10-5受拉伸载荷作用的紧螺栓联接中，为什么总载荷不是预紧力和拉伸载荷之和？
[解] 因为螺栓和被联接件都是弹性体。

10-6 螺纹副的效率与哪些因素有关？为什么多线螺纹多用于传动，普通三角螺纹主要用于联接，而梯形、矩形、锯齿形螺纹主要用于传动？
[解] 与线数、螺距和当量摩擦角有关。

因数越多，效率越高。

当量摩擦角v ρ，在摩擦系数一定的情况下，牙型斜角β越大，则当量摩擦角v ρ越大，效率越低，自锁性能越好，所以在螺旋传动中，为了提高效率，采用牙型斜角β小的螺纹，如矩形螺纹、梯形螺旋传动中，为了提高效率，采用了提高自锁性能，应采用牙型斜角大的螺纹，如三角形螺纹。

10-7 螺纹副的自锁条件是什么？
[解] 螺纹副的自锁条件为 v λρ≤。

第10 章 螺纹连接与螺旋传动四、简答题2.螺纹为什么要防松？防松方法有哪些？各适用于什么场合？答：用于联接的普通螺纹一般都具有自锁性，在静载荷作用下不会自动松脱。

但在（1）冲击、振动或变载荷下，螺纹副和支承面间的磨擦力会下降；（2）在温度变化中，联接件与被联接件之间的温度变形有差异，或发生蠕变，使预紧力或摩擦力减小，甚至松脱。

因此在设计时就应注意螺纺联接的防松问题。

防松的根本问题是阻止螺纹副的相对转动。

具体防松措施有三种：（1）摩擦防松（弹簧垫圈、双螺母、尼龙圈锁紧螺母等）；（2）机械防松（开口销与槽形螺母、止动热圈等）；（3）破坏性防松（冲击、粘合等）。

机械防松和摩擦防松称为可拆卸防松，而破坏性防松称为不可拆卸防松。

五、计算题2．用两个10M 的螺钉固定一牵曳钩，若螺钉材料为Q235，装配时控制预紧力，接合面磨擦系数15.0=f ，求其允许的牵曳力。

、解：解 查教材表10-6得 Q235的屈服极限MPa S 235=σ，查教材表10-6得，当控制预紧力时，取安全系数3.1=S 由许用应力 MPa S S 1813.1235][===σσ查教材表10-1得 10M 的小径mm d 376.81= 由公式[]σπσ==4/3.121d F a e 得 预紧力 N d F a76683.14376.81813.14/][221=⨯⨯⨯==ππσ由题图可知1=m ，螺钉个数2=z ，取可靠性系数3.1=C 牵曳力 N Cmf zF F a 17703.115.0176682=⨯⨯⨯==3.两根梁用8个6.8级普通螺栓与两块钢盖板相联接，梁受到的拉力kN 40=F ，摩擦系数15.0=f ，控制预紧力。

试确定所需螺栓直径。

FF解：已知螺栓数目8z =，结合面数2m =,取防滑系数 1.2f k =,则螺栓所需预紧力F’为1.240000'20000..0.1582t K F F N z m μ⨯===⨯⨯查表10-6得240s Mpa σ=，安全系数 1.3s S =，则得[]240/1.3184.6S s S Mpa σσ===所需螺栓直径：14 1.32000013.4184.6d mm π⨯⨯==⨯圆整后得螺栓尺寸16d mm =,故螺纹为M16.4.图示的凸缘联轴器，材料为HT200，用8个M16的螺栓联接，螺栓性能等级为8.8级。

机械设计第⼗章齿轮设计课后习题答案机械设计第⼗章齿轮设计课后习题答案10-2解（1）齿轮A为主动轮，齿轮B为“惰轮”，也就是说齿轮B既是主动轮⼜是从动轮。

当齿轮B与主动轮A啮合时，⼯作齿⾯是王侧，当齿轮B与从动轮C啮合时，⼯作齿⾯是另⼀侧。

对于⼀个轮齿来讲，是双齿⾯⼯作双齿⾯受载，弯曲应⼒是对称循环，接触⼒是脉动循环，取10-3 答：齿⾯接触应⼒是脉动循环，齿根弯曲应⼒是对称循环。

在作弯曲强度计算时，应将图中查出的极限应⼒值乘以0.7. 10-4 答：⼀般齿轮材料主要选⽤锻钢（碳钢或全⾦钢）。

对于精度要求较低的齿轮，将齿轮⽑坯经正⽕或调质处理后切齿即为成，这时精度可达8级，精切合⾦钢主要是渗碳后淬⽕，最后进⾏滚齿等精加⼯，其精度可达7，6级甚或5级。

对于尺⼨较⼤的齿轮，可适⽤铸钢或球墨铸铁，正⽕后切齿也可达8级精度。

10-5提⾼轮齿抗弯疲劳强度的措施有：增⼤齿根过渡圆⾓半径，消除加⼯⼑痕，可降低齿根应⼒集中;增⼤轴和⽀承的则度，可减⼩齿⾯局部受载；采取合适的热处理⽅法使轮世部具有⾜够的韧性；在齿根部进⾏喷丸、滚压等表⾯强度，降低齿轮表⾯粗糙度，齿轮采⽤正变位等。

提⾼齿⾯抗点蚀能⼒的措施有：提⾼齿⾯硬度；降低表⾯粗糙度；增⼤润滑油粘度；提⾼加⼯、发装精度以减⼩动载荷；在许可范围内采⽤较⼤变位系数正传动，可增⼤齿轮传动的综合曲率半径。

10-6解（1）选⽤齿轮的材料和精度等级，由教材表10-1可知，⼤⼩齿轮材料均为45号钢调质，⼩齿轮齿⾯硬度为250HBS,⼤齿轮齿⾯硬度为220HBS.选精度等级为7级。

（2）按齿⾯接触疲劳强度设计。

1、⼩齿轮传递的转矩2、初选载荷系数：初选Kt=1.83、确定齿宽系数：⼩齿轮不对称布置，据教材表10-7选⽤4、确定弹性影响系数：据教材表10-6查得5、确定区域载荷系数：按标准直齿圆柱齿轮传动设计ZH=2.56、齿数⽐：7、确定接触许⽤应⼒：循环次数查教材图10-19曲线I得查教材10-21（d）得8、由接触强度计算⼩齿轮的分度圆直径齿轮的使⽤系数：载荷状况以轻微冲击为依据查教材表10-2得KA=1.25齿轮的圆周速度由教材图10-8查得：Kv=1.12对于软齿⾯齿轮，假设,由教材表10-3查得齿宽齿宽与齿⾼⽐由教材表10-4查得,由教材图10-13查得：,接触强度载荷系数：10、校正直径：取标准值m=2.5mm11、齿轮的相关参数：12、确定齿宽：圆整后，取b2=50mm,b1=55mm.(3)校核齿根弯曲疲劳强度。

机械设计第十章习题答案机械工程学系资料机械设计第十章习题答案10-1 试分析图10-47所示的齿轮传动各齿轮所受的力（用受力图表示的里的作用位置及方向）。

解：受力图如下：机械工程学系资料注：斜齿轮各个受力方向1. 径向力指向各自的轴心；2. 轴向力的方向按主动轮螺旋线方向和转向，右旋用右手，左旋用左手，四肢弯曲方向与主动轮转向一致，拇指即为主动轮轴向力方向；3. 圆周力的方向在主动轮上，与运动方向相反；从动轮上，与运动方向相同。

10-6 设计铣床中的一对圆柱齿轮传动，已知1 = 7.5 kW，1 = 1450 r/min ，1 = 26 ，2 = 54 ，寿命= 12022年h ，小齿轮相对其轴承的支撑为不对称布置，并画出大齿轮的机构图。

解：1. 选择齿轮类型、精度等级、材料（1 ）选用直齿圆柱齿轮传动（2 ）铣床为工作母机，速度不高，故选用6级精度（GB__-88 ）。

（3 ）材料选择由表10-1选择小齿轮材料为20CrMnTi（渗碳后淬火），60HRC ，大齿轮材料为40Cr（调质后表面淬火），53HRC 。

2. 按齿面接触强度设计1 ≥32 1+12（（1 ）确定公式中的各计算值1 ）试选载荷系数= 1.4 机械工程学系资料2 ）计算小齿轮传递的力矩1 = 9.55 × 106 ×7.__1 1= 9.55 × 106 ×= __.55 Nmm3 ）小齿轮作不对称布置，查表10-7 ，选取= 0.94 ）由表10-5查得材料的弹性影响系数= 189.85 ）确定区域系数= 2.56 ）计算接触疲劳强度用重合度系数1 = arcos [ 29.241°2 = arcos [ 25.024°= =26 × tan29.241° tan20° +54 × tan20.024° tan20°21 tan tan ′ +2 tan tan ′22cos2+211cos1+2] = arcos26cos20°26+2 ×1=] = arcos54cos20°54+2 ×1== 1.694 = 7 ）齿数比u =2 14 3=4 1.6943= 0.877= 2.088 ）计算接触疲劳许用应力由小齿轮20CrMnTi ，渗碳后淬火，得1机械工程学系资料= 1300 MPa由大齿轮40Cr ，调质后淬火，得2 = 1300 MPa9 ）计算应力循环次数1 , 21 = 60 1 j = 60 × 1450 × 1 × 12022年= 1.044 ×1092 =1= 5.02 × 10810 ）确定接触疲劳寿命系数由图10-23 ，查表得：1 = 0.95 ，2 = 0.9511 ）计算接触疲劳许用应力取失效概率1% ，安全系数S = 1 [ ] 1 = 1368.42 MPa [ ] 2 = 1368.42 MPa得[ ] = 1368.42 MPa （2 ）计算1 ≥ =331 lim 1=0.95 ×13001=2 lim 2=0.95 ×13001=2 1+12 ×1.4 __.550.8×2.08+1 2.08× (2.5 ×189.8 ×0.87921368.42机械工程学系资料= 28.71 mm 圆周速度v = m/s（3 ）计算齿宽bb = × 1 = 0.8 × 28.71 = 22.97 mm（4 ）计算齿宽和吃高比1 160 × 1000=×28.71 __ ×1000= 2.18=1 1=28.7126= 1.10齿宽h = 2.25 = 2.48 mm 因而= 9.26（5 ）计算载荷系数1 ）使用系数= 1.252 ）动载系数由v = 2.18 m/s ，6级精度，取= 1.04 3 ）齿间载荷分配系数直齿轮及修行齿轮，取= 1 ，= 14 ）齿向载荷分布系数由= 0.8 ，硬齿面，非对称布置，6级精度，b = 22,97 mm ，线性插值得= 1.284 ，由= 9.26 ，= 1.284得=机械工程学系资料1.26载荷系数K = = 1.25 × 1.04 × 1 × 1.284 = 1.67（6 ）按实际载荷系数算得分度圆直径1 = 1 = 28.71 × =1.4331.6730.45 mm（7 ）计算模数mm = = 1.17mm3. 按齿根弯曲强度设计由弯曲疲劳强度的计算公式m ≥32 11（1 ）确定公式各变量的值1 ）由小齿轮：渗碳淬火钢1 = 850 MPa 由大齿轮：调制后表面淬火2 = 720 MPa2 ）取弯曲疲劳寿命系数1 = 0.91 , 2 = 0.93 3 ）计算弯曲许用应力取安全系数S = 1.4 ，由[ ] = 得[ ]1 = MPa1 1=0.91 ×8501.4= 552.5机械工程学系资料[ ]2 = MPa4 ）计算[ ]2 2=0.93 ×7201.4= 478.29由图10-17 ，10-18查取齿形系数得1 = 2.60 ，1 = 1.5950.0082181.26 = 1.6380.6932 = 2.296 ，2 = 1.712 1 1[ ]1 = 0.__-__2 2[ ]2= 0.008128可见大齿轮的数值大一些，取较大值5 ）计算载荷系数K = = 1.25 × 1.04 × 1 ×6 ）计算弯曲疲劳强度重合度系数由10-5得=0.25 + 0.75= 0.25 +0.751.694=2 ）试算模数3≥ 2 11=32 ×1.638 __.55 ×0.6390.8 × 26 ×0.008128= 1.194 mm（机械工程学系资料4. 结果分析和选择对比两种计算方法，可以看出齿根弯曲疲劳强度m ≥ 1.194mm及按齿面接触算得的模数m ≥ 1.17 ，故可取m ≥ 1.194 mm ，将模数标准化圆整，取m =2 mm 。

一、课本10-2 解：（1）B 轮是惰轮，齿根弯曲应力是对称循环变应力。

查图10-21d)，接触疲劳极限应力MPa 580lim =H σ，弯曲疲劳极限应力MPa 3084407.0=⨯=FE σ。

许用应力为：MPa 58015801][lim =⨯==S K H HN H σσ；MPa 2964.13081][=⨯==S K FE FN F σσ （2）B 轮是主动轮，齿根弯曲应力是脉动循环变应力。

查图10-21d)，接触疲劳极限应力MPa 580lim =H σ，弯曲疲劳极限应力MPa 440=FE σ。

许用应力为：MPa 58015801][lim =⨯==S K H HN H σσ；MPa 3144.1440][===S K FE FN F σσ 如齿轮的工作寿命不是无限寿命时，上述两种情况下的许用应力值均相应增大。

二、课本10-7 解：该齿轮传动的承载能力由齿面接触强度所限定。

1．计算按齿面接触强度所限定的转矩，由式（10-21）得：()2311][12⎪⎪⎭⎫ ⎝⎛⋅+≤E H H d z z u K u d T σεφα1）小齿轮分度圆直径 mm 95.145229cos 246cos 11='︒⨯==βz m d n 。

2）齿宽系数 096.195.1451601===d b d φ。

3）查图10-26，765.01=αε，925.02=αε端面重合度 685.1925.0765.021=+=+=αααεεε。

4）齿数比 5.42410812===z z u 。

5）由表10-6查得材料的弹性影响系数 21MPa 8.189=E z 。

6）由图10-30查得区域系数 455.2=H z 。

7）小齿轮合金钢调质260HBS ，由图10-21d 查得小齿轮的接触疲劳极限MPa 5801lim =H σ；大齿轮碳钢调质220HBS ，由图10-21d 查得大齿轮的接触疲劳极限MPa 5202lim =H σ。