濮良贵机械设计第九版课后习题答案
- 格式:doc
- 大小:1.39 MB
- 文档页数:38

第三章 机械零件的强度习题答案3-1某材料的对称循环弯曲疲劳极限MPa 1801=-σ,取循环基数60105⨯=N ,9=m ,试求循环次数N 分别为7 000、25 000、620 000次时的有限寿命弯曲疲劳极限。
[解] MPa 6.373107105180936910111=⨯⨯⨯==--N N σσN3-2已知材料的力学性能为MPa260=s σ,MPa1701=-σ,2.0=σΦ,试绘制此材料的简化的等寿命寿命曲线。
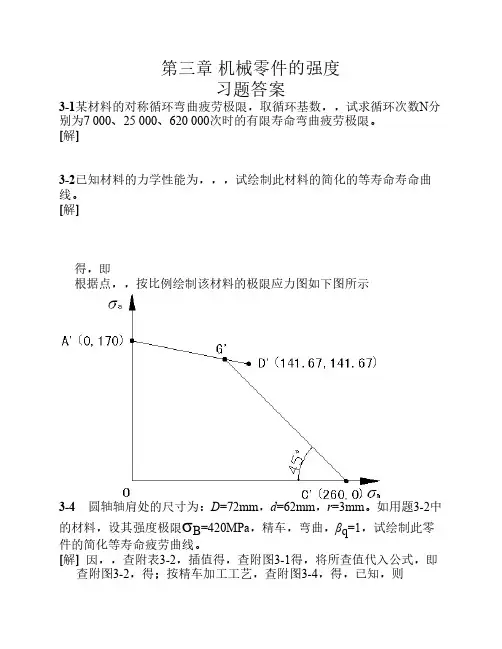
[解] )170,0('A )0,260(C得)233.283,233.283(D ',即)67.141,67.141(D '根据点)170,0('A ,)0,260(C ,)67.141,67.141(D '按比例绘制该材料的极限应力图如下图所示3-4 圆轴轴肩处的尺寸为:D =72mm ,d =62mm ,r =3mm 。
如用题3-2中的材料,设其强度极限σB =420MPa ,精车,弯曲,βq =1,试绘制此零件的简化等寿命疲劳曲线。
[解] 因2.14554==d D ,067.0453==d r ,查附表3-2,插值得88.1=ασ,查附图3-1得78.0≈σq ,将所查值代入公式,即查附图3-2,得75.0=σε;按精车加工工艺,查附图3-4,得91.0=σβ,已知1=q β,则根据()()()29.60,67.141,0,260,34.72,0D C A 按比例绘出该零件的极限应力线图如下图3-5 如题3-4中危险截面上的平均应力MPa 20m =σ,应力幅MPa 20a =σ,试分别按①C r =②Cσ=m ,求出该截面的计算安全系数ca S 。
[解] 由题3-4可知35.2,2.0MPa,260MPa,170s 1-====σσK Φσσ(1)C r =工作应力点在疲劳强度区,根据变应力的循环特性不变公式,其计算安全系数 (2)C σ=m工作应力点在疲劳强度区,根据变应力的平均应力不变公式,其计算安全系数第五章螺纹连接和螺旋传动习题答案5-5图5-49是由两块边板和一块承重板焊接的龙门起重机导轨托架。

第三章 机械零件的强度习题答案3-1某材料的对称循环弯曲疲劳极限MPa 1801=-σ,取循环基数60105⨯=N ,9=m ,试求循环次数N 分别为7 000、25 000、620 000次时的有限寿命弯曲疲劳极限。
[解] MPa 6.373107105180936910111=⨯⨯⨯==--N N σσN MPa 3.324105.2105180946920112=⨯⨯⨯==--N N σσN MPa 0.227102.6105180956930113=⨯⨯⨯==--N N σσN 3-2已知材料的力学性能为MPa 260=s σ,MPa 1701=-σ,2.0=σΦ,试绘制此材料的简化的等寿命寿命曲线。
[解] )170,0('A )0,260(C 012σσσΦσ-=- σΦσσ+=∴-1210 MPa 33.2832.0117021210=+⨯=+=∴-σΦσσ 得)233.283,233.283(D ',即)67.141,67.141(D '根据点)170,0('A ,)0,260(C ,)67.141,67.141(D '按比例绘制该材料的极限应力图如下图所示3-4圆轴轴肩处的尺寸为:D=72mm,d=62mm,r=3mm。
如用题3-2中的材料,设其强度极限σB=420MPa,精车,弯曲,βq=1,试绘制此零件的简化等寿命疲劳曲线。
[解] 因2.14554==dD,067.0453==dr,查附表3-2,插值得88.1=ασ,查附图3-1得78.0≈σq,将所查值代入公式,即()()69.1188.178.0111k=-⨯+=-α+=σσσq查附图3-2,得75.0=σε;按精车加工工艺,查附图3-4,得91.0=σβ,已知1=qβ,则35.211191.0175.069.1111k=⨯⎪⎭⎫⎝⎛-+=⎪⎪⎭⎫⎝⎛-+=qσσσσββεK()()()35.267.141,67.141,0,260,35.2170,0DCA∴根据()()()29.60,67.141,0,260,34.72,0DCA按比例绘出该零件的极限应力线图如下图3-5如题3-4中危险截面上的平均应力MPa20m=σ,应力幅MPa20a=σ,试分别按①C r =②C σ=m ,求出该截面的计算安全系数ca S 。
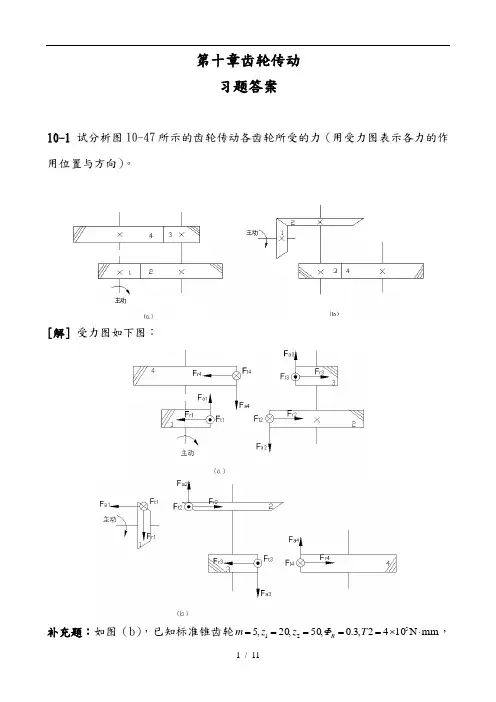
第十章齿轮传动 习题答案10-1 试分析图10-47所示的齿轮传动各齿轮所受的力(用受力图表示各力的作用位置与方向)。
[解] 受力图如下图:补充题:如图(b ),已知标准锥齿轮mm N 1042,3.0,50,20,5521⋅⨯=====T Φz z m R ,标准斜齿轮24,63==z m n ,若中间轴上两齿轮所受轴向力互相抵消,β应为多少?并计算2、3齿轮各分力大小。
[解](1)齿轮2的轴向力:()222222222sin tan 5.012sin tan 2sin tan δαz Φm T δαdm T δαF F R t a -=== 齿轮3的轴向力:βz m T ββz m T βd T βF F n n t a sin 2tan cos 2tan 2tan 33333333=⎪⎪⎭⎫ ⎝⎛=== 3232,20,T T αF F a a =︒==()βz m T δαz Φm T n R sin 2sin tan 5.01233222=-∴即()2235.01sin tan sin z Φm δαz m βR n -=由5.22050tan 122===z z δ 928.0sin 2=∴δ371.0cos 2=δ ()()2289.0503.05.015928.020tan 2465.01sin tan sin 223=⨯⨯-⨯⨯︒⨯⨯=-=∴z Φm δαz m βR n即︒=231.13β (2)齿轮2所受各力:()() 3.765kN N 10765.3503.05.01510425.01223522222=⨯=⨯⨯-⨯⨯⨯=-==z Φm T dm T F R t0.508kNN 10508.0371.020tan 10765.3cos tan 33222=⨯=⨯︒⨯⨯==δαF F t r kN 272.1N 10272.1928.020tan 10765.3sin tan 33222=⨯=⨯︒⨯⨯==δαF F t akN 420cos 10765.3cos 322=︒⨯==αF F t n齿轮3所受各力:kN 408.5N 10408.5231.13cos 2461042cos 2cos 22353232333=⨯=︒⨯⨯⨯==⎪⎪⎭⎫ ⎝⎛==βz m T βz m T d T F n n tkN 022.2N 10022.2321.12cos 20tan 10408.5cos tan 3333=⨯=︒︒⨯⨯==βαF F n t rkN 272.1N 10272.1321.12cos 20tan 10408.5tan 10408.5tan 33333=⨯=︒︒⨯⨯⨯⨯==βF F t akN 889.5N 10889.5321.12cos 20cos 10765.3cos cos 3333=⨯=︒︒⨯==βαF F n t n10-6设计铣床中的一对圆柱齿轮传动,已知54,26min,r 1450,kW 5.72111====z z n P ,寿命h 12000=h L ,小齿轮相对其轴的支承为不对称布置,并画出大齿轮的机构图。


第三章 机械 零件的强度p45习题答案3-1某材料的对称循环弯曲疲劳 极限MPa 1801=-σ,取循环基数60105⨯=N ,9=m ,试求循环次数 N分别为7 000、25 000、620 000次时的有限寿命弯曲疲劳极限。
[解] MPa 6.373107105180936910111=⨯⨯⨯==--N N σσN M P a 3.324105.2105180946920112=⨯⨯⨯==--N N σσN M P a 0.227102.6105180956930113=⨯⨯⨯==--N N σσN 3-2已知材料的力学 性能为MPa 260=s σ,MPa 1701=-σ,2.0=σΦ,试绘制此材料的简化的等寿命寿命曲线。
[解] )170,0('A )0,260(C 012σσσΦσ-=- σΦσσ+=∴-121M P a 33.2832.0117021210=+⨯=+=∴-σΦσσ得)233.283,233.283(D ',即)67.141,67.141(D '根据点)170,0('A ,)0,260(C ,)67.141,67.141(D '按比例绘制该材料的极限应力图 如下图所示3-4 圆轴轴肩处的 尺寸为:D =72mm ,d =62mm ,r =3mm 。
如用题3-2中的材料,设其强度极限σB =420MPa ,精车,弯曲,βq =1,试绘制此零件的简化等 寿命疲劳曲线。
[解] 因2.14554==d D ,067.0453==d r ,查附表3-2,插值得88.1=ασ,查附图3-1得78.0≈σq ,将所查值代入公式,即()()69.1188.178.0111k =-⨯+=-α+=σσσq查附图3-2,得75.0=σε;按精车加工工艺,查附图3-4,得91.0=σβ,已知1=q β,则35.211191.0175.069.1111k =⨯⎪⎭⎫ ⎝⎛-+=⎪⎪⎭⎫ ⎝⎛-+=q σσσσββεK ()()()35.267.141,67.141,0,260,35.2170,0D C A ∴根据()()()29.60,67.141,0,260,34.72,0D C A 按比例 绘出该零件的极限应力线图如下图3-5 如题3-4中危险截面上的平均应力MPa 20m =σ,应力幅MPa 20a =σ,试分别按①C r =②C σ=m ,求出该截 面的计算安全系数ca S 。


第三章 机械零件的强度p45习题答案3-1某材料的对称循环弯曲疲劳极限MPa 1801=-σ,取循环基数60105⨯=N ,9=m ,试求循环次数N 分别为7 000、25 000、620 000次时的有限寿命弯曲疲劳极限。
[解] MPa 6.373107105180936910111=⨯⨯⨯==--N N σσN MPa 3.324105.2105180946920112=⨯⨯⨯==--N N σσNMPa 0.227102.6105180956930113=⨯⨯⨯==--N N σσN 3-2已知材料的力学性能为MPa 260=s σ,MPa 1701=-σ,2.0=σΦ,试绘制此材料的简化的等寿命寿命曲线。
[解] )170,0('A )0,260(C 0012σσσΦσ-=-ΘσΦσσ+=∴-1210MPa 33.2832.0117021210=+⨯=+=∴-σΦσσ得)233.283,233.283(D ',即)67.141,67.141(D '根据点)170,0('A ,)0,260(C ,)67.141,67.141(D '按比例绘制该材料的极限应力图如下图所示3-4 圆轴轴肩处的尺寸为:D =72mm ,d =62mm ,r =3mm 。
如用题3-2中的材料,设其强度极限σB =420MPa ,精车,弯曲,βq =1,试绘制此零件的简化等寿命疲劳曲线。
[解] 因2.14554==dD,067.0453==d r,查附表3-2,插值得88.1=ασ,查附图3-1得78.0≈σq ,将所查值代入公式,即()()69.1188.178.0111k =-⨯+=-α+=σσσq查附图3-2,得75.0=σε;按精车加工工艺,查附图3-4,得91.0=σβ,已知1=q β,则35.211191.0175.069.1111k =⨯⎪⎭⎫ ⎝⎛-+=⎪⎪⎭⎫ ⎝⎛-+=q σσσσββεK ()()()35.267.141,67.141,0,260,35.2170,0D C A ∴根据()()()29.60,67.141,0,260,34.72,0D C A 按比例绘出该零件的极限应力线图如下图3-5 如题3-4中危险截面上的平均应力MPa 20m =σ,应力幅MPa 20a =σ,试分别按①C r =②C σ=m ,求出该截面的计算安全系数ca S 。
第三章 机械零件的强度习题答案3-1某材料的对称循环弯曲疲劳极限MPa 1801=-σ,取循环基数60105⨯=N ,9=m ,试求循环次数N分别为7 000、25 000、620 000次时的有限寿命弯曲疲劳极限。
[解] MPa 6.373107105180936910111=⨯⨯⨯==--N N σσN MPa 3.324105.2105180946920112=⨯⨯⨯==--N N σσN MPa 0.227102.6105180956930113=⨯⨯⨯==--N N σσN 3-2已知材料的力学性能为MPa 260=s σ,MPa 1701=-σ,2.0=σΦ,试绘制此材料的简化的等寿命寿命曲线。
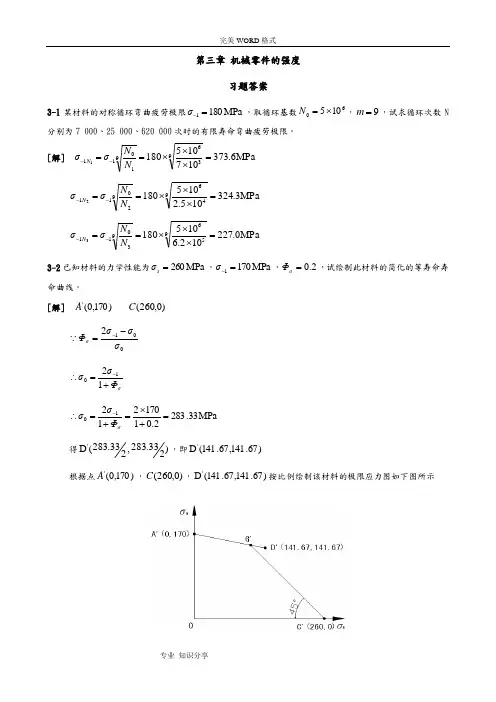
[解] )170,0('A )0,260(C 012σσσΦσ-=- σΦσσ+=∴-121MPa 33.2832.0117021210=+⨯=+=∴-σΦσσ得)233.283,233.283(D ',即)67.141,67.141(D '根据点)170,0('A ,)0,260(C ,)67.141,67.141(D '按比例绘制该材料的极限应力图如下图所示3-3一圆轴轴肩处的尺寸为:D =72mm ,d =62mm ,r =3mm 。
材料为40CrNi ,设其强度极限σB =900MPa ,屈服极限750MPa s σ=试计算周健的弯曲有效应力集中系数k σ。
[解] 因1.16D d =,0.048rd=,查附表3-2,插值得 1.995σα=,查附图3-1得78.0≈σq ,将所查值代入公式,即()()k 1110.78 1.9951 1.896σσσq α=+-=+⨯-=3-4圆轴轴肩处的尺寸为:D =54mm ,d =45mm ,r =3mm 。
如用题3-2中的材料,设其强度极限σB=420MPa ,试绘制此零件的简化等寿命疲劳曲线。
[解] 因2.14554==d D ,067.0453==d r ,查附表3-2,插值得88.1=ασ,查附图3-1得78.0≈σq ,将所查值代入公式,即()()69.1188.178.0111k =-⨯+=-α+=σσσq查附图3-2,得0.7σε=;按精车加工工艺,查附图3-4,得91.0=σβ,已知1=q β,则k 11 1.691111 2.510.70.911σσσσq K εββ⎛⎫⎛⎫=+-=+-⨯= ⎪ ⎪⎝⎭⎝⎭()()()170141.670,,260,0,141.67,2.512.51A C D ∴根据()()()0,67.73,260,0,141.67,56.44A C D 按比例绘出该零件的极限应力线图如下图3-5 如题3-4中危险截面上的平均应力MPa 20m =σ,应力幅MPa 20a =σ,试分别按①C r =②C σ=m ,求出该截面的计算安全系数ca S 。
第三章 机械零件的强度习题答案3-1某材料的对称循环弯曲疲劳极限MPa 1801=-σ,取循环基数60105⨯=N ,9=m ,试求循环次数N 分别为7 000、25 000、620 000次时的有限寿命弯曲疲劳极限。
[解] MPa 6.373107105180936910111=⨯⨯⨯==--N N σσN MPa 3.324105.2105180946920112=⨯⨯⨯==--N N σσN MPa 0.227102.6105180956930113=⨯⨯⨯==--N N σσN 3-2已知材料的力学性能为MPa 260=s σ,MPa 1701=-σ,2.0=σΦ,试绘制此材料的简化的等寿命寿命曲线。
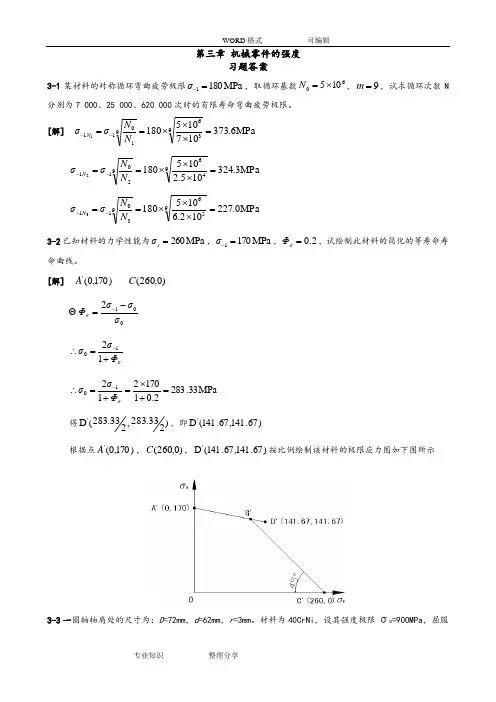
[解] )170,0('A )0,260(C 012σσσΦσ-=- σΦσσ+=∴-121MPa 33.2832.0117021210=+⨯=+=∴-σΦσσ得)233.283,233.283(D ',即)67.141,67.141(D '根据点)170,0('A ,)0,260(C ,)67.141,67.141(D '按比例绘制该材料的极限应力图如下图所示3-3一圆轴轴肩处的尺寸为:D =72mm ,d =62mm ,r =3mm 。
材料为40CrNi ,设其强度极限σB =900MPa ,屈服极限750MPa s σ=试计算周健的弯曲有效应力集中系数k σ。
[解] 因1.16D d =,0.048rd=,查附表3-2,插值得 1.995σα=,查附图3-1得78.0≈σq ,将所查值代入公式,即()()k 1110.78 1.9951 1.896σσσq α=+-=+⨯-=3-4圆轴轴肩处的尺寸为:D =54mm ,d =45mm ,r =3mm 。
如用题3-2中的材料,设其强度极限σB=420MPa ,试绘制此零件的简化等寿命疲劳曲线。
[解] 因2.14554==d D ,067.0453==d r ,查附表3-2,插值得88.1=ασ,查附图3-1得78.0≈σq ,将所查值代入公式,即()()69.1188.178.0111k =-⨯+=-α+=σσσq查附图3-2,得0.7σε=;按精车加工工艺,查附图3-4,得91.0=σβ,已知1=q β,则k 11 1.691111 2.510.70.911σσσσq K εββ⎛⎫⎛⎫=+-=+-⨯= ⎪ ⎪⎝⎭⎝⎭()()()170141.670,,260,0,141.67,2.51 2.51A C D ∴ 根据()()()0,67.73,260,0,141.67,56.44A C D 按比例绘出该零件的极限应力线图如下图3-5 如题3-4中危险截面上的平均应力MPa 20m =σ,应力幅MPa 20a =σ,试分别按①C r =②C σ=m ,求出该截面的计算安全系数ca S 。

WORD 格式 可编写第三章 机械部件的强度习题答案3-1 某资料的对称循环波折疲倦极限σ1180MPa ,取循环基数 N 0 5 106 , m 9 ,试求循环次数 N分别为 7 000 、 25 000 、 620 000 次时的有限寿命波折疲倦极限。
[ 解 ]σ1N 1σ1 9N 0 180 95 106373.6MPaN 17 103σ1N 2σ1 9 N 018095 106324.3MPaN 22.5 10 4σ1N 3σ19 N 018095 106227.0MPaN 36.2 10 53-2 已知资料的力学性能为 σs260MPa , σ1 170MPa , Φσ 0.2 ,试绘制此资料的简化的等寿命寿命曲线。
[ 解 ]A ' (0,170)C( 260,0)σ1σΦσ2 0σ0σ2σ11 Φσσ2σ1 2 170283.33MPa1 Φσ 1 0.2得 D '(283.332 ,283.332) ,即 D ' (141.67,141.67)依照点 A ' (0,170) , C (260,0) , D ' (141.67,141.67) 按比率绘制该资料的极限应力求以以下列图所示3-3 一圆轴轴肩处的尺寸为: D =72mm , d =62mm , r =3mm 。
资料为 40CrNi ,设其强度极限σB=900MPa ,信服WORD 格式可编写极限 σ750MPa 试计算周健的波折有效应力集中系数k 。
s[解] 因D1.16 ,r0.048 ,查附表 3-2 ,插值得σ1.995 ,查附图 3-1 得 q σ0.78 ,将所查值dd代入公式,即k σ 1 q σ σ 1 1 0.78 1.995 1 1.8963-4 圆轴轴肩处的尺寸为: D =54mm , d =45mm , r =3mm 。
如用题 3-2 中的资料,设其强度极限σ B=420MPa ,试绘制此部件的简化等寿命疲倦曲线。
第三章 机械零件的强度欧阳家百(2021.03.07)习题答案3-1某材料的对称循环弯曲疲劳极限MPa 1801=-σ,取循环基数60105⨯=N ,9=m ,试求循环次数N 分别为7 000、25 000、620 000次时的有限寿命弯曲疲劳极限。
[解] MPa 6.373107105180936910111=⨯⨯⨯==--N N σσN 3-2已知材料的力学性能为MPa 260=s σ,MPa 1701=-σ,2.0=σΦ,试绘制此材料的简化的等寿命寿命曲线。
[解] )170,0('A )0,260(C得)233.283,233.283(D ',即)67.141,67.141(D '根据点)170,0('A ,)0,260(C ,)67.141,67.141(D '按比例绘制该材料的极限应力图如下图所示3-4 圆轴轴肩处的尺寸为:D =72mm ,d =62mm ,r =3mm 。
如用题3-2中的材料,设其强度极限σB =420MPa ,精车,弯曲,βq =1,试绘制此零件的简化等寿命疲劳曲线。
[解] 因2.14554==d D ,067.0453==d r ,查附表3-2,插值得88.1=ασ,查附图3-1得78.0≈σq ,将所查值代入公式,即查附图3-2,得75.0=σε;按精车加工工艺,查附图3-4,得91.0=σβ,已知1=q β,则根据()()()29.60,67.141,0,260,34.72,0D C A 按比例绘出该零件的极限应力线图如下图3-5 如题3-4中危险截面上的平均应力MPa 20m =σ,应力幅MPa20a =σ,试分别按①C r =②C σ=m ,求出该截面的计算安全系数ca S 。
[解] 由题3-4可知35.2,2.0MPa,260MPa,170s 1-====σσK Φσσ (1)C r =工作应力点在疲劳强度区,根据变应力的循环特性不变公式,其计算安全系数 (2)C σ=m工作应力点在疲劳强度区,根据变应力的平均应力不变公式,其计算安全系数第五章 螺纹连接和螺旋传动习题答案5-5 图5-49是由两块边板和一块承重板焊接的龙门起重机导轨托架。
机械设计课后习题答案濮良贵第三章机械零件的强度p45习题答案3-1某材料的对称循环弯曲疲劳极限MPa 1801=-ζ,取循环基数60105?=N ,9=m ,试求循环次数N 分别为7 000、25 000、620 000次时的有限寿命弯曲疲劳极限。
[解] MPa 6.373107105180936910111===--N N ζζN M P a 3.324105.2105180946920112===--N N ζζNM P a 0.227102.6105180956930113===--N N ζζN 3-2已知材料的力学性能为MPa 260=s ζ,MPa 1701=-ζ,2.0=ζΦ,试绘制此材料的简化的等寿命寿命曲线。
[解])170,0('A)0,260(C012ζζζΦζ-=-ζΦζζ+=∴-1210M P a 33.2832.0117021210=+?=+=∴-ζΦζζ 得)233.283,233.283(D ',即)67.141,67.141(D '根据点)170,0('A ,)0,260(C ,)67.141,67.141(D '按比例绘制该材料的极限应力图如下图所示3-4 圆轴轴肩处的尺寸为:D =72mm ,d =62mm ,r =3mm 。
如用题3-2中的材料,设其强度极限σB =420MPa ,精车,弯曲,βq =1,试绘制此零件的简化等寿命疲劳曲线。
[解] 因2.145 54==dD ,067.0453==d r,查附表3-2,插值得88.1=αζ,查附图3-1得78.0≈ζq ,将所查值代入公式,即()()69.1188.178.0111k =-?+=-α+=ζζζq查附图3-2,得75.0=ζε;按精车加工工艺,查附图3-4,得91.0=ζβ,已知1=q β,则35.211191.0175.069.1111k = ??-+= ??-+=q ζζζζββεK ()()()35.267.141,67.141,0,260,35.2170,0D C A ∴根据()()()29.60,67.141,0,260,34.72,0D C A 按比例绘出该零件的极限应力线图如下图3-5 如题3-4中危险截面上的平均应力MPa 20m =ζ,应力幅MPa 20a =ζ,试分别按①C r =②C ζ=m ,求出该截面的计算安全系数ca S 。
第三章 机械零件的强度习题答案3-1某材料的对称循环弯曲疲劳极限MPa 1801=-σ,取循环基数60105⨯=N ,9=m ,试求循环次数N分别为7 000、25 000、620 000次时的有限寿命弯曲疲劳极限。
[解] MPa 6.373107105180936910111=⨯⨯⨯==--N N σσN MPa 3.324105.2105180946920112=⨯⨯⨯==--N N σσN MPa 0.227102.6105180956930113=⨯⨯⨯==--N N σσN 3-2已知材料的力学性能为MPa 260=s σ,MPa 1701=-σ,2.0=σΦ,试绘制此材料的简化的等寿命寿命曲线。
[解] )170,0('A )0,260(C 012σσσΦσ-=-Θ σΦσσ+=∴-121MPa 33.2832.0117021210=+⨯=+=∴-σΦσσ得)233.283,233.283(D ',即)67.141,67.141(D '根据点)170,0('A ,)0,260(C ,)67.141,67.141(D '按比例绘制该材料的极限应力图如下图所示3-3一圆轴轴肩处的尺寸为:D =72mm ,d =62mm ,r =3mm 。
材料为40CrNi ,设其强度极限σB =900MPa ,屈服极限750MPa s σ=试计算周健的弯曲有效应力集中系数k σ。
[解] 因1.16D d =,0.048rd=,查附表3-2,插值得 1.995σα=,查附图3-1得78.0≈σq ,将所查值代入公式,即()()k 1110.78 1.9951 1.896σσσq α=+-=+⨯-=3-4圆轴轴肩处的尺寸为:D =54mm ,d =45mm ,r =3mm 。
如用题3-2中的材料,设其强度极限σB=420MPa ,试绘制此零件的简化等寿命疲劳曲线。
[解] 因2.14554==d D ,067.0453==d r ,查附表3-2,插值得88.1=ασ,查附图3-1得78.0≈σq ,将所查值代入公式,即()()69.1188.178.0111k =-⨯+=-α+=σσσq查附图3-2,得0.7σε=;按精车加工工艺,查附图3-4,得91.0=σβ,已知1=q β,则k 11 1.691111 2.510.70.911σσσσq K εββ⎛⎫⎛⎫=+-=+-⨯= ⎪ ⎪⎝⎭⎝⎭()()()170141.670,,260,0,141.67,2.51 2.51A C D ∴根据()()()0,67.73,260,0,141.67,56.44A C D 按比例绘出该零件的极限应力线图如下图3-5 如题3-4中危险截面上的平均应力MPa 20m =σ,应力幅MPa 20a =σ,试分别按①C r =②C σ=m ,求出该截面的计算安全系数ca S 。
第三章 机械零件的强度习题答案3-1某材料的对称循环弯曲疲劳极限MPa 1801=-σ,取循环基数60105⨯=N ,9=m ,试求循环次数N 分别为7 000、25 000、620 000次时的有限寿命弯曲疲劳极限。
[解] MPa 6.373107105180936910111=⨯⨯⨯==--N N σσN MPa 3.324105.2105180946920112=⨯⨯⨯==--N N σσN MPa 0.227102.6105180956930113=⨯⨯⨯==--N N σσN 3-2已知材料的力学性能为MPa 260=s σ,MPa 1701=-σ,2.0=σΦ,试绘制此材料的简化的等寿命寿命曲线。
[解] )170,0('A )0,260(C 012σσσΦσ-=- σΦσσ+=∴-1210 MPa 33.2832.0117021210=+⨯=+=∴-σΦσσ 得)233.283,233.283(D ',即)67.141,67.141(D '根据点)170,0('A ,)0,260(C ,)67.141,67.141(D '按比例绘制该材料的极限应力图如下图所示3-4 圆轴轴肩处的尺寸为:D =72mm ,d =62mm ,r =3mm 。
如用题3-2中的材料,设其强度极限σB =420MPa ,精车,弯曲,βq =1,试绘制此零件的简化等寿命疲劳曲线。
[解] 因2.14554==d D ,067.0453==d r ,查附表3-2,插值得88.1=ασ,查附图3-1得78.0≈σq ,将所查值代入公式,即()()69.1188.178.0111k =-⨯+=-α+=σσσq查附图3-2,得75.0=σε;按精车加工工艺,查附图3-4,得91.0=σβ,已知1=q β,则35.211191.0175.069.1111k =⨯⎪⎭⎫ ⎝⎛-+=⎪⎪⎭⎫ ⎝⎛-+=qσσσσββεK ()()()35.267.141,67.141,0,260,35.2170,0D C A ∴ 根据()()()29.60,67.141,0,260,34.72,0D C A 按比例绘出该零件的极限应力线图如下图3-5 如题3-4中危险截面上的平均应力MPa 20m =σ,应力幅MPa 20a =σ,试分别按①C r =②C σ=m ,求出该截面的计算安全系数ca S 。
[解] 由题3-4可知35.2,2.0MPa,260MPa,170s 1-====σσK Φσσ(1)C r =工作应力点在疲劳强度区,根据变应力的循环特性不变公式,其计算安全系数 28.2202.03035.2170m a 1-=⨯+⨯=+=σΦσK σS σσca(2)C σ=m工作应力点在疲劳强度区,根据变应力的平均应力不变公式,其计算安全系数 ()()()()81.1203035.2202.035.2170m a m 1-=+⨯⨯-+=+-+=σσσσca σσK σΦK σS第五章 螺纹连接和螺旋传动习题答案5-5 图5-49是由两块边板和一块承重板焊接的龙门起重机导轨托架。
两块边板各用4个螺栓与立柱相连接,托架所承受的最大载荷为20kN ,载荷有较大的变动。
试问:此螺栓连接采用普通螺栓连接还是铰制孔用螺栓连接为宜?为什么?Q215,若用M 6×40铰孔用螺栓连接,已知螺栓机械性能等级为8.8,校核螺栓连接强度。
[解] 采用铰制孔用螺栓连接为宜因为托架所受的载荷有较大变动,铰制孔用螺栓连接能精确固定被连接件的相对位置,并能承受横向载荷,增强连接的可靠性和紧密性,以防止受载后被连接件间出现缝隙或发生相对滑移,而普通螺栓连接靠结合面产生的摩擦力矩来抵抗转矩,连接不牢靠。
(1)确定M 6×40的许用切应力[τ]由螺栓材料Q215,性能等级8.8,查表5-8,可知MPa 640][s =σ,查表5-10,可知0.5~5.3][=τS()MPa 128~86.1820.5~5.3640][][][s ===τ∴τS σMPa 67.4265.1640][s ===p p S σσ (2)螺栓组受到剪力F 和力矩(FL T =),设剪力F 分在各个螺栓上的力为i F ,转矩T 分在各个螺栓上的分力为j F ,各螺栓轴线到螺栓组对称中心的距离为r ,即mm 27545cos 2150=︒=rkN 2510275810300208 kN5.220818133=⨯⨯⨯⨯===⨯==∴--r FL F F F j i 由图可知,螺栓最大受力kN 015.945cos 255.22)25(5.2cos 22222max =︒⨯⨯⨯++=++=θF F F F F j i j i()][319106410015.9423320max τ>=⨯⨯π⨯=π=τ∴-d F][8.131104.1110610015.9333min 0max p p σL d F σ<=⨯⨯⨯⨯==∴--故M 6×40的剪切强度不满足要求,不可靠。
5-6 已知一个托架的边板用6个螺栓与相邻的机架相连接。
托架受一与边板螺栓组的垂直对称轴线相平行、距离为250mm 、大小为60kN 的载荷作用。
现有如图5-50所示的两种螺栓布置形式,设采用铰制孔用螺栓连接,试问哪一种布置形式所用的螺栓直径最小?为什么?[解] 螺栓组受到剪力F 和转矩,设剪力F 分在各个螺栓上的力为i F ,转矩T 分在各个螺栓上的分力为j F(a )中各螺栓轴线到螺栓组中心的距离为r ,即r =125mmkN 2010125610250606 kN 1060616133=⨯⨯⨯⨯===⨯==∴--r FL F F F ji 由(a )图可知,最左的螺栓受力最大kN 302010max =+=+=j i F F F (b )方案中kN 10606161=⨯==F F ikN 39.24101252125421252101252125102506062223223612max612maxmax =⨯⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛⨯+⎪⎭⎫ ⎝⎛⨯⨯+⎪⎭⎫ ⎝⎛⨯⨯⨯===---==∑∑i ii ij rFLr rMr F 由(b )图可知,螺栓受力最大为kN 63.335239.24102)39.24(10cos 22222max =⨯⨯⨯++=++=θF F F F F j i j i []直径较小)布置形式所用的螺栓可知采用(由a F d τπ≥∴max045-10第六章 键、花键、无键连接和销连接习题答案6-3 在一直径mm 80=d 的轴端,安装一钢制直齿圆柱齿轮(如下图),轮毂宽度1.5d L =,工作时有轻微冲击。
试确定平键的尺寸,并计算其允许传递的最大扭矩。
[解] 根据轴径mm 80=d ,查表得所用键的剖面尺寸为mm 22=b ,mm 14=h根据轮毂长度mm 120805.1'=⨯==1.5d L 取键的公称长度 mm 90=L 键的标记 键79-90GB 109622⨯键的工作长度为 68mm 2290=-=-=b L l 键与轮毂键槽接触高度为 mm 7==2h k根据齿轮材料为钢,载荷有轻微冲击,取许用挤压应力 110MPa ][=p σ根据普通平键连接的强度条件公式 ][1023p p σkldT σ≤⨯=变形求得键连接传递的最大转矩为m N 20942000110806872000][⋅=⨯⨯⨯==p max σkld T第八章 带传动 习题答案8-1 V 带传动的m in 14501r n =,带与带轮的当量摩擦系数51.0=v f ,包角︒=α1801,初拉力N 3600=F 。
试问:(1)该传动所能传递的最大有效拉力为多少?(2)若mm 100d d1=,其传递的最大转矩为多少?(3)若传动效率为0.95,弹性滑动忽略不计,从动轮输出效率为多少?[解] ()N 4.4781111360211112151.01151.00=+-⨯⨯=+-=ππααee e e F F v vf f ec ()m m N 92.232101004.4782d 2-3d1⋅=⨯⨯==ec F T()kW45.395.0100060100010014.314504.4781000601000d 10003d11=⨯⨯⨯⨯⨯⨯=•⨯⨯π=•=ηn F ηνF P ec ec8-2 V 带传动传递效率7.5kW =P ,带速s m 10=ν,紧边拉力是松边拉力的两倍,即21F F =,试求紧边拉力1F 、有效拉力e F 和初拉力0F 。
[解] 1000νF P e =N 750105.710001000=⨯==∴νP F e21212F F F F F e =-=且 1500N 750221=⨯==∴e F F201eF F F += 1125N 27501500210=-=-=∴e F F F8-4 有一带式输送装置,其异步电动机与齿轮减速器之间用普通V 带传动,电动机功率P=7kW ,转速m in 9601r n =,减速器输入轴的转速m in 3302r n =,允许误差为%5±,运输装置工作时有轻度冲击,两班制工作,试设计此带传动。
[解] (1)确定计算功率ca P由表8-7查得工作情况系数2.1A =K ,故 4kW .872.1A ca =⨯==P K P (2)选择V 带的带型根据ca P 、1n ,由图8-11选用B 型。
(3)确定带轮的基准直径d d ,并验算带速ν①由表8-6和8-8,取主动轮的基准直径mm 1801=d d②验算带速νs m 0432.9100060960180********=⨯⨯⨯π=⨯π=n d νd带速合适∴<<m 30s m 5ν③计算从动轮的基准直径 ()()mm 45.49733005.0196018012112=-⨯⨯=-=n εn d d d d(4)确定V 带的中心距a 和基准长度d L①由式()()2102127.0d d d d d d a d d +≤≤+,初定中心距mm 5500=a 。
②计算带所需的基准长度()()()()mm221455041805005001802550242222122100≈⨯-++π+⨯=-++π+≈a d d d d a L d d d d d由表8-2选带的基准长度mm 2240=d L ③实际中心距a mm 563222142240550200=-+=-+≈d d L L a a 中心距的变化范围为mm 630~550。