《归纳、类比、演绎推理》课件
- 格式:ppt
- 大小:968.50 KB
- 文档页数:24


演绎推理归纳推理类比推理一、演绎推理演绎推理是一种基于逻辑关系的推理方式,通过观察事实和已知的前提条件,从中推导出结论。
演绎推理遵循严密的逻辑思维规则,从而保证了推理的准确性和可靠性。
1. 演绎推理的基本原理演绎推理的基本原理是从已知的事实或前提出发,通过逻辑推导得出结论。
它主要依赖于以下三大要素:•前提条件:演绎推理的起点是一组已知的前提条件或已验证的事实,它们被假定为真实和可信的。
•规则/原则:演绎推理遵循一系列严谨的逻辑规则和推理原则,如假言推理、析取范式、消解和推理规则等,以确保推理的有效性。
•结论:通过对前提条件的逻辑分析和推导,得出一个更加确凿的结论。
2. 演绎推理的例子以下是一个简单的演绎推理示例:•前提条件1:所有人类都会呼吸。
•前提条件2:约翰是一个人类。
•推导:根据前提条件1,我们知道所有人类都会呼吸。
根据前提条件2,约翰是一个人类。
因此,根据演绎推理的原理,我们可以得出结论:约翰会呼吸。
通过以上示例,我们可以看到演绎推理的过程是基于已知的前提条件,通过逻辑推导得出结论的。
二、归纳推理归纳推理是一种通过具体事例或观察到的模式来推断普遍规律的推理方法。
它基于从一组特殊情况中归纳出一般性结论的思维过程。
1. 归纳推理的过程归纳推理的过程可以分为以下几个步骤:•收集和观察具体的实例。
•分析这些实例之间的共同点和规律。
•通过对这些共同点和规律的归纳,提出一般性结论。
•验证结论的普适性。
归纳推理常用于科学研究、实证研究以及一些从具体案例中总结经验和规律的场景中。
2. 归纳推理的例子以下是一个归纳推理的例子:•实例1:小明看到小猫是黄色的。
•实例2:小红看到小猫是黄色的。
•实例3:小李看到小猫是黄色的。
通过观察以上实例,我们可以归纳得出结论:小猫是黄色的。
这是因为我们在多个实例中都观察到了相同的模式,即小猫的颜色都是黄色的。
三、类比推理类比推理是一种基于相似性的推理方法,通过将一个问题或情境与另一个已解决的问题或情境进行比较,从而得出结论。





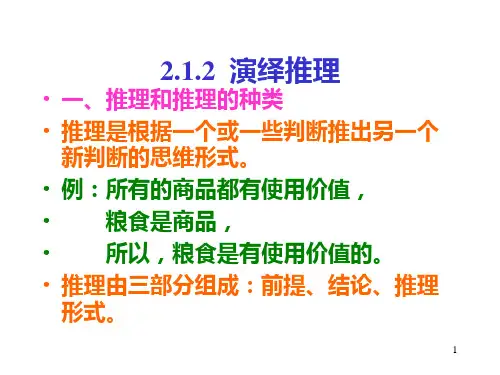
演绎法归纳法类比法一、演绎法从一般性的原理出发,推出某个特殊情况下的结论,这种推理就是演绎推理,也叫逻辑推理。
简而言之,演绎推理是由一般到特殊的推理。
演绎推理的一般模式为“三段论”,即:(1)大前提:已知的一般原理;(2)小前提:所研究的特殊情况;(3)结论:根据一般原理,对特殊情况做出的判断。
【例题】证明函数),在(12)(2∞-+-=x x x f 内是增函数。
分析:本题中大前提为:在某个区间),(b a 内,如果0)(>'x f ,那么函数)(x f y =在这个区间内单调递增。
小前提为:x x x f 2)(2+-=的导数在区间)1,(-∞内满足0)(>'x f ,是证明本题的关键。
证明:22)(+-='x x f当)1,(-∞∈x 时,有01>-x所以0)1(222)(>-=+-='x x x f即根据“三段论”得,)1,(2)(2-∞+-=在x x x f 内是增函数.在演绎推理中,只要前提和推理形式是正确的,结论必定是正确的.二、归纳法由某类事物的部分对象具有某些特征,推出该类事物的全部对象都具有这些特征的推理,或者由个别事实概括出一般结论的推理,称为归纳推理(简称归纳)。
简而言之,归纳推理是由部分到整体、由个别到一般的推理。
归纳推理的思维过程大致是:实验、观察→概括、推广→猜测一般性结论。
该过程包括两个步骤:(1)通过观察个别对象发现某些相同的性质;(2)从已知的相同性质中推出一个明确表述的一般性命题(猜想)。
【例题】已知数列11}{1=a a n 项的第,且),3,2,1(11 =+=+n a a a nn n ,试归纳除这个数列的通项公式。
解:当1=n 时,数列的第1项11=a ; 当2=n 时,数列的第2项211112=+=a ; 当3=n 时,数列的第3项31211213=+=a ; 当4=n 时,数列的第4项41311314=+=a . 观察可知,数列的前4项都等于相应序号的倒数. 由此猜想,这个数列的通项公式为na n 1=.三、类比法由两类对象具有某些类似特征和其中一类对象的某些已知特征,推出另一类对象也具有这些特征的推理称为类比推理(简称类比)。



逻辑学全部ppt课件CONTENTS •逻辑学概述•形式逻辑•辩证逻辑•数理逻辑初步•归纳逻辑与演绎逻辑•逻辑谬误与批判性思维逻辑学概述01逻辑学的定义与研究对象逻辑学的定义逻辑学是研究推理和论证的学科,旨在分析、评估和改进人们的思维方式和表达方法。
研究对象逻辑学的研究对象包括概念、命题、推理、论证等思维形式和规律。
起源于古希腊,代表人物有亚里士多德等,主要研究三段论等演绎推理方法。
19世纪末至20世纪初,数理逻辑得到快速发展,代表人物有弗雷格、罗素等,将数学方法应用于逻辑学研究。
随着计算机科学、人工智能等领域的发展,逻辑学在多个领域得到广泛应用,形成了多个分支学科。
古典逻辑学近现代逻辑学当代逻辑学逻辑学的发展历程03辩证思维方法在分析和评估论证过程中,运用辩证思维方法来揭示论证中的矛盾和问题,提出改进意见。
01形式化方法通过符号和公式来表示概念、命题和推理,运用形式化系统进行推导和证明。
02语义分析方法研究语言表达式与客观世界之间的关系,分析表达式的意义和真值条件。
逻辑学的研究方法形式逻辑02概念与范畴概念的定义与分类解释概念的含义,探讨概念的种类及其之间的关系。
范畴的划分与特性阐述范畴的概念,分析范畴的划分标准及其特性。
概念与范畴的关系探讨概念与范畴之间的联系与区别,以及它们在逻辑学中的地位和作用。
判断与推理判断的构成与种类分析判断的基本要素,介绍判断的种类及其逻辑特征。
推理的形式与规则阐述推理的含义,探讨推理的形式和规则,包括演绎推理和归纳推理等。
判断与推理的关系探讨判断与推理之间的联系与区别,以及它们在逻辑学中的地位和作用。
形式化方法形式化语言与符号系统介绍形式化语言的概念,阐述符号系统的构建原则和方法。
形式化证明与演算探讨形式化证明的方法和技巧,包括自然演绎、公理化方法等,以及形式化演算的基本规则和步骤。
形式化方法的应用阐述形式化方法在逻辑学、数学、计算机科学等领域的应用及其意义。
辩证逻辑03整体性辩证思维强调从整体上把握事物,注重事物之间的相互联系和相互作用。