当前位置：文档之家 › 第八讲 序列相关性

第八讲 序列相关性

  • 格式：ppt
  • 大小：424.00 KB
  • 文档页数：66

下载文档原格式

  / 66

合集下载

序列相关性

序列相关性

yt 1 2 Pt 1 ut
5.滞后效应 在经济中，因变量受到自身或另一解释变量的前几期值影响的现象称为 滞后效应。在一个消费支出对收入的时间序列回归中，人们常常发现当前时 期的消费支出除了依赖于其他变量外，还依赖于前期的消有效 因为，在有效性证明中利用了 E(NN’)=2I 即同方差性和互相独立性条件。而且，在大样本情况下，参数估计量 虽然具有一致性，但仍然不具有渐近有效性。 2、变量的显著性检验失去意义 在变量的显著性检验中，统计量是建立在参数方差正确估计基础之 上的，这只有当随机误差项具有同方差性和互相独立性时才能成立。如果存 在序列相关，估计的参数方差 S ˆ ，出现偏误（偏大或偏小） ，t 检验就失去
~ e ~ e t t 1 t
，
~ e ~ ~ e t 1 t 1 2 et 2 t
3
， 。 。 。
醉客天涯之计量经济学
如果存在某一种函数形式，使得方程显著成立，则说明原模型存在序列相关性。 回归检验法的优点是： （1）能够确定序列相关的形式 （2）适用于任何类型序列相关性问题的检验。 3、杜宾-瓦森（Durbin-Watson）检验法（最常用） （1）方法使用条件： ①解释变量 X 非随机； ②随机误差项 i 为一阶自回归形式： i=i-1+i ③回归模型中不应含有滞后应变量作为解释变量，即不应出现下列形式： Yi=0+1X1i+kXki+Yi-1+i ④回归含有截距项 ⑤误差项被假定为正态分布 （2）D.W.统计量： 杜宾和瓦森针对原假设：H0: =0， 即不存在一阶自回归，构如下造统计量：
D.W .
~ (e
t 2
n
t
~ )2 e t 1
2 t
《序列相关性》课件

《序列相关性》课件


序列相关性的类型
01
02
03
正相关
当一个观测值增加时，另 一个观测值也增加，反之 亦然。
负相关
当一个观测值增加时，另 一个观测值减少，反之亦 然。
无相关性
两个观测值之间不存在明 显的依赖关系。
序列相关性产生的原因
01
02
03
04
季节性影响
某些时间序列数据会受到季节 性因素的影响，导致观测值之
间存在周期性依赖关系。
偏相关系数检验
总结词
偏相关系数检验是一种用于检验时间序列数据之间是否存在长期均衡关系的统计方法。
详细描述
偏相关系数检验基于时间序列数据的偏相关图，通过计算偏相关系数，判断时间序列数 据之间是否存在长期均衡关系。如果存在长期均衡关系，则说明时间序列数据之间存在
某种稳定的关联性，可能存在协整关系。
04 序列相关性对模型的影响
个体差异性和时间趋势性。
02 03
序列相关性分析
面板数据的序列相关性分析是对不同个体或区域上的时间序列数据进行 相关性检验和建模的过程，主要考察不同个体或区域在同一时间点上的 数据是否具有相关性。
总结
面板数据的序列相关性分析是研究面板数据的重要手段，有助于揭示不 同个体或区域在同一时间点上的数据关联和动态变化。
经济因素
经济活动中的各种因素可能导 ຫໍສະໝຸດ 时间序列数据之间存在相关性。
政策因素
政策变动或干预可能对时间序 列数据产生影响，导致观测值
之间存在相关性。
其他因素
如气候变化、人口增长等也可 能对时间序列数据产生影响， 导致观测值之间存在相关性。
02 序列相关性在统计学中的 应用
线性回归模型中的序列相关性
什么是序列相关性如何进行序列相关性的检验与处理

什么是序列相关性如何进行序列相关性的检验与处理

什么是序列相关性如何进行序列相关性的检验与处理序列相关性是指一系列数据中存在的相关性或依赖关系。

它可以帮助我们了解数据的趋势、周期性以及对未来数据的预测。

在统计学中，序列相关性的检验和处理是非常重要的，可以帮助我们提取有用的信息和建立可靠的模型。

本文将介绍序列相关性的定义、如何进行序列相关性的检验以及处理方法。

一、序列相关性的定义序列相关性是指时间序列数据中的观察值之间的相关性或依赖关系。

当一个时间序列的观察值和它之前或之后的观察值之间存在关联时，就可以说这个时间序列是相关的。

序列相关性表明序列中的数据点之间存在某种模式或趋势，这对于分析和预测时间序列数据具有重要意义。

二、序列相关性的检验为了检验时间序列数据是否存在相关性，我们可以使用常用的统计方法，例如自相关函数（ACF）和偏自相关函数（PACF）。

自相关函数是衡量一个时间序列和其滞后版本之间相关性的统计指标。

它可以帮助我们确定序列中的周期性模式。

在自相关函数图中，横轴表示滞后阶数，纵轴表示相关系数。

如果自相关函数在某个滞后阶数上超过了置信区间，那么可以认为有相关性存在。

偏自相关函数是衡量一个时间序列和其滞后版本之间相关性的统计指标，消除了其他滞后版本的影响。

在偏自相关函数图中，横轴表示滞后阶数，纵轴表示相关系数。

如果偏自相关函数在某个滞后阶数上超过了置信区间，那么可以认为有相关性存在。

另外，我们还可以使用单位根检验（ADF检验）来检验序列是否平稳。

平稳序列的相关性更容易进行建模和预测。

如果序列通过了单位根检验，那么就可以认为序列是平稳的。

三、序列相关性的处理如果时间序列数据存在相关性，那么我们可以采取一些方法进行处理，以消除或减小相关性的影响。

首先，可以进行差分操作。

差分是指将时间序列的每个观察值与其滞后版本之间的差异进行计算。

差分后的序列通常更容易建模，因为它们消除了相关性。

如果还存在差分后的序列中的相关性，可以继续进行更高阶的差分操作。

中级计量经济学 第八讲

中级计量经济学 第八讲

This assumption implies that ut is uncorrelated with any of the xkj. 这个假定可推出ut 与任何xkj都不相关。
分析截面数据时，如果我们把数据按特定方式排序，序列相关的问 题也可能发生，然而由于系统产存在时间上的惰性，它在时间序列 分析中更为常见。
For this reason it is often called autocorrelation.
因为这个原因，它常常被称作是自相关。
4
Basic Regression Analysis with Time Series Data
定理 10.1 (OLS的无偏性):在假定TS.1-3下，OLS估计量 条件于X是无偏的，因此也是无条件无偏。
7
The assumption TS2
假定 TS2
We need to discuss more about TS2. It assumes that E(ut|X)=0, t=1,…,n, where X denotes all the independent variables in all the time periods. 我们需要更多的讨论关于TS2。它假定了E(ut|X)=0, t=1,…,n, 其中X表示所有时期的所有自变量。
Testing for Serial Correlation 检验序列相关
Correcting for Serial Correlation with Strictly Exogenous Regressors 当自变量为严格外生时校正序列相关
Differencing and Serial Correlation 差分和序列相关
Properties of OLS with Serially Correlated Errors 误差序列相关时OLS的性质
序列相关性名词解释

序列相关性名词解释

序列相关性名词解释
序列相关又称自相关，是指总体回归模型的随机误差项之间存在相关关系。

序列相关性在计量经济学中指对于不同的样本值，随机干扰之间不再是完全相互独立的，而是存在某种相关性。

序列相关即不同观测点上的误差项彼此相关。

序列相关产生的原因有很多，一般认为主要有一下几种，经济变量惯性的作用引起随机误差项自相关，经济行为的滞后性引起随机误差项自相关，一些随机偶然因素的干扰引起随机误差项自相关，模型设定误差引起随机误差项自相关，观测数据处理引起随机误差项序列相关。

一般经验告诉我们，对于采用时间序列数据作样本的计量经济学问题，由于在不同样本点上解释变量以外的其他因素在时间上的连续性，带来它们对被解释变量的影响的连续性，所以往往存在序列相关性。

序列相关性

序列相关性


（四）拉格朗日乘数检验（Lagrange Multiplier）
• LM检验是由布劳殊（Breusch）与戈弗雷（Godfrey） 于1978年提出的，也被称为GB检验。 • 拉格朗日乘数检验克服了DW检验的缺陷，适合于高阶序 列相关以及模型中存在滞后被解释变量的情形。
对于模型
Yt 0 1 X1t 2 X 2t k X kt t
§4.2
序列相关性
一、序列相关性的概念
二、实际经济问题中的序列相关性
三、序列相关性的后果
四、序列相关性的检验
五、序列相关性的补救
四、序列相关性的检验
基本思路 ：
首先， 采用 OLS 法估计模型， 以得随机误差项的
~ e i 表示： “近似估计量” ，用
~ Y (Y ˆ) e i i i 0 ls
t 2 n t
n
t 1
其中：ρ为一阶自相关系数
) 2(1 )
et 2 ~
t 1
一阶自回归模型：i=i-1+i 的参数估计。
由于自相关系数的值介于－1和＋1之间，因此：
0≤DW≈2(1-ρ)≤4 如果存在完全一阶正相关，即=1，则 D.W. 0 完全一阶负相关，即= -1, 则 D.W. 4 完全不相关，即=0，则 D.W.2

检验时需要事先确定准备检验的阶数P,实际检验中，可从1阶、2
阶、…逐次向更高阶检验。

检验结果显著时，可以说明存在序列相关，但是并不一定代表序列 相关的阶数一定能够达到所检验的阶数。
◦ 低阶序列相关的存在往往会导致高阶序列相关检验的显著性 ◦ 具体阶数的判断，需要结合辅助回归中自相关系数的显著性
4-dL
# D.W.检验统计量的说明
计量经济学试题计量经济学中的序列相关性与解决方法

计量经济学试题计量经济学中的序列相关性与解决方法

计量经济学试题计量经济学中的序列相关性与解决方法计量经济学试题: 计量经济学中的序列相关性与解决方法序列相关性是计量经济学中重要的概念之一，它描述了时间序列数据之间的相关程度。

在许多经济学研究中，序列相关性可能会导致问题，如伪回归和自相关误差。

为了解决这些问题，研究人员采用了一些方法来处理序列相关性。

本文将介绍序列相关性的定义、影响和解决方法。

一、序列相关性的定义序列相关性是指一组时间序列数据之间存在的相关关系。

它反映了一个变量的当前值与过去值的相关程度。

序列相关性可以判断变量之间是否存在依赖关系，以及时间趋势的演变和预测。

在计量经济学中，序列相关性通常使用自相关函数(acf)和偏自相关函数(pacf)来度量。

自相关函数衡量了序列与其自身在不同滞后期的相关性，而偏自相关函数则控制了其他滞后期的效应。

二、序列相关性的影响序列相关性对计量经济分析的结果具有重要影响。

当存在序列相关性时，经济学模型的估计结果可能会产生偏误。

这是因为序列相关性违反了线性回归模型的基本假设，导致参数估计失真。

此外，当序列相关性存在时，标准误差和t统计量的计算也会出现问题。

标准误差的计算通常基于误差项的无关性假设，而序列相关性违反了这一假设，导致标准误差被低估。

因此，对参数的显著性检验将失去准确性。

三、解决序列相关性的方法为了解决序列相关性的问题，计量经济学提出了许多方法和技术。

下面介绍几种常用的解决方法。

1. 差分法(Differencing Method)差分法是通过对时间序列数据进行差分，消除序列相关性的方法。

差分法可以消除序列的线性趋势，使数据变得稳定。

这种方法利用变量的差分来消除序列的相关性，使得模型的估计结果更可靠。

2. 自相关修正法(Autoregressive Model)自相关修正法是通过引入滞后变量来建模序列相关性。

自相关修正模型考虑变量的滞后值与当前值之间的关系，以控制序列相关性的影响。

常见的自相关修正模型包括自回归移动平均模型(ARMA)和自回归条件异方差模型(ARCH)。

计量经济学-序列相关性

计量经济学-序列相关性


PART 03
序列相关性检验方法
杜宾-瓦特森检验
检验原理
通过计算残差序列的一阶自相关系数来检验序列相关性。
检验步骤
首先估计回归模型，计算残差；然后计算残差的自相关系数；最后 根据自相关系数和样本量确定临界值，判断序列相关性。
优缺点
简单易行，但仅适用于一阶自相关的情况，对于高阶自相关检验效 果较差。
将检验结果以表格或图形形式展示出 来，包括检验统计量、P值等。若存 在序列相关性，可采用差分法、 ARIMA模型等方法进行处理，并重新 进行参数估计和检验。
根据检验结果和处理结果，对模型的 适用性和可靠性进行评估。若模型存 在严重序列相关性问题，则需要重新 考虑模型设定和估计方法。
PART 06
总结与展望
检验步骤
在原始回归模型中添加滞后项作为解释变量；然后估计辅 助回归模型，得到回归系数的估计值；最后根据回归系数 的估计值构造统计量，进行假设检验。
优缺点
可以检验任意阶数的自相关，但需要注意滞后项的选择和 模型的设定。
PART 04
序列相关性处理方法
差分法
一阶差分法
通过计算相邻两个时期的数据差值来消除序列相 关性。
运用最小二乘法（OLS）或其他估计方法，对模型参数进行估计。在 EViews中，可通过"Quick"菜单选择"Estimate Equation"选项进行参数估 计。
序列相关性检验及处理结果展示
01
序列相关性检验
02
处理结果展示
03
结果解读
采用Durbin-Wu-Hausman检验、 Breusch-Godfrey检验等方法，检验 模型是否存在序列相关性。在EViews 中，可通过"View"菜单选择 "Residual Diagnostics"选项进行检 验。
序列相关性、多重共线性

序列相关性、多重共线性

序列相关性、多重共线性序列相关性概念序列相关性是指模型残差之间存在相关性。

来源经济变量固有的惯性模型设定的偏差，遗漏了重要的变量或者是函数的形式不正确数据的“编造”，模型的数据有些是由原始数据⽣成的后果影响估计量的有效性解释变量的显著性失效模型的预测失效检验思路是假设不存在，使⽤OLS估计得出相应的估计量画残差图做回归检验分析做D—W检验，缺陷是只能是做⼀阶序列相关性的检验⼴义拉格朗⽇乘数法，⼜称为GB检验，能够做⾼阶的序列相关性检验，检验出到底是⼏阶序列相关性解决⽅法⼴义最⼩⼆乘法科伦奥科特模型（Eviews内部使⽤的⽅法）⼴义差分模型（差分项要⽐⽔平项的相关性⼩的多）虚假序列相关性问题模型由于遗漏变量等问题，⽽导致了序列相关性，⼀般来说先构造⼀个⼀般的模型，然后使⽤逐步回归的⽅法去进⾏分析多重共线性（Multi-Collinearity）概念多重共线性是指解释变量之间存在相关性，分为两类，完全共线性和近似共线性（交互相关性）来源更多的是⼀种数据问题，⽽不是模型设定的问题。

经济变量之间的共同趋势滞后变量的引⼊样本资料的限制后果在完全共线性下，参数估计是不存在的。

估计量⾮有效，会导致估计量的⽅差膨胀，VIF。

估计量的经济含义不明确解释变量的显著性失去意义（包含显著性和系数的⽅向）检验检验的⽬标在于两点，是否存在多重共线性，确定哪些变量之间存在解释变量之间的相关系数检验逐步回归排除某个变量，看⽅程的拟合优度是不是没有变化，如果是说明这个变量对于⽅程的贡献度很⼩，很可能会存在多重共线性问题。

解决⽅法排除某个变量使⽤⼴义差分的⽅法，差分项的线性关系远⽐⽔平项的线性关系弱得多减少估计变量的⽅差，扩⼤样本容量，岭回归⽅法。

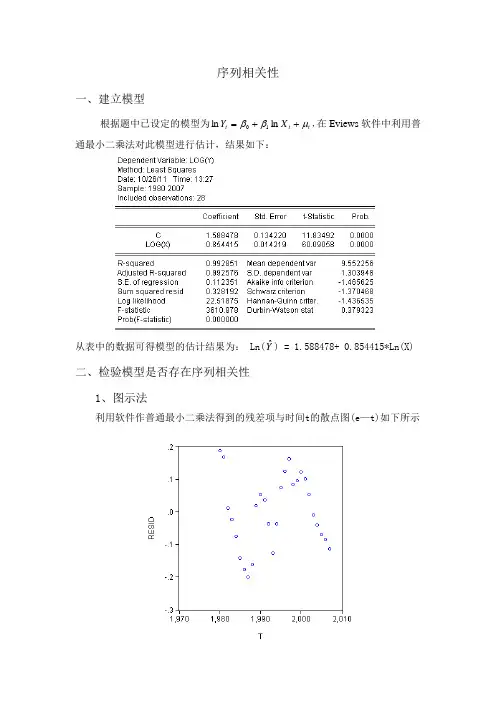
序列相关性

序列相关性

序列相关性一、建立模型根据题中已设定的模型为t t t X Y μββ++=ln ln 10，在Eviews 软件中利用普通最小二乘法对此模型进行估计，结果如下：从表中的数据可得模型的估计结果为： Ln(Yˆ) = 1.588478+ 0.854415*Ln(X) 二、检验模型是否存在序列相关性1、图示法利用软件作普通最小二乘法得到的残差项与时间t 的散点图(e —t)如下所示由(e—t)图可看出残差t e~随时间t的变化同增大或同减小，即呈现一定的正相关性。

2、D.W.检验在5%显著性水平下，该模型样本个数n=28,解释变量个数k=2(包含常数项)，查表可得d L =1.33，d U =1.48，而由最小二乘法得到的模型估计表中可看到D.W.=0.379323＜1.33，故存在正序列相关性。

三、确定自相关性的阶数对用普通最小二乘法估计的模型作拉格朗日乘数（LM）检验，利用Eviews 软件得到阶数=1的检验如下表：由上表数据得LM统计量nR2的P值=0.0001显著的小于0.05，而且一阶滞后残差项e~t-1的t统计量的P值显著的小于0.05；故序列存在一阶自相关性。

下面检验阶数=2时是否有相关性：当阶数为2时，利用软件中的LM检验,输入阶数2，结果如下表由上表数据得LM统计量nR2的P值显著的小于0.05，而且一阶滞后残差项e~t-1与二阶滞后变量e~t-2的t统计量的P值均显著的小于0.05；故序列存在二阶自相关性。

下面检验阶数=3时是否有相关性：利用软件中的LM检验，在对话框中输入阶数3，得到结果如下表：由上表数据可发现LM统计量nR2的P值为0.0003显著的小于0.05，说明原模型仍存在序列相关性，但是三阶滞后残差项e~t-3的t统计量的P值为0.7140大于显著性水平0.05，表明序列不存在三阶自相关性，所以原模型存在显著的二阶序列相关性。

四、用广义差分法进行自相关的处理由于原模型存在二阶序列相关性，利用Eviews软件，选择常数项c、log(x)、AR（1）、AR（2）作为解释变量，用普通最小二乘法估计方程可得到广义差分的参数估计，估计结果如下表：由表中数据可得D.W.=1.819703，而在5%显著性水平下，该广义差分模型样本个数n=26,解释变量个数k=4（包含常数项），查表得: d L=1.14，d U=1.65,由于1.65＜1.819703＜4-1.65，即d U＜D.W.＜4-d U，所以用广义差分法处理后的模型不存在序列相关性。

序列相关性

序列相关性

序列相关性
序列相关性（SequenceCorrelation）是一种重要的统计学技术，它用来衡量和分析两个或多个相关序列之间的关系，以检测和预测未来的变化。

它最早出现在电信行业，用于诊断信号传输出现的问题。

随着数字信号处理技术在各个领域的普及，序列相关性也被用于科学、工程、金融和经济等许多领域，以检测和预测未来的变化。

序列相关性通常是指两个或多个相关时间序列之间的相关性，即两个序列中时间上相邻元素之间的空间关系。

它以线性方式来衡量数据集之间的相关性，反映出其内在的结构和未来的变化趋势。

序列相关性的测量可以使用线性回归的方法，也可以使用非线性方法，例如波动率，均值行走和自相关函数。

这些方法用于通过检测输入序列中存在的规律性，预测时间序列中未来的变化。

例如，均值行走可以用于分析具有相同或类似序列趋势的时间序列，从而预测未来的变化。

序列相关性也可以用于比较数据集之间的关系，例如销售数据、价格数据和交易数据等。

这种研究可以揭示不同因素对销售情况的影响，从而帮助管理者做出有效的营销决策。

此外，序列相关性可以帮助投资者识别投资组合，以便减少投资风险和收益率波动。

它也可以用于评估金融市场中风险和投资回报的关系。

序列相关性有助于揭示数据间隐藏的关系，并预测未来的变化
趋势。

它也可以用于比较数据集之间的关系，可以帮助投资者识别投资组合，以及评估金融市场中风险和投资回报的关系。

因此，序列相关性在许多行业的应用非常普遍，帮助企业在投资和运营方面取得更好的成绩。

序列相关性的基本原理包括

序列相关性的基本原理包括序列相关性是指两个或多个序列之间的关系或相互关联程度。

在统计学和时间序列分析中，序列相关性是一种基本的概念，用于描述序列之间的相关性。

了解序列相关性的基本原理可以帮助我们理解和分析时间序列数据以及其他类型的序列数据。

序列相关性的基本原理包括：1. 相关性的度量方法：序列相关性可以通过相关系数来度量。

常用的相关系数有皮尔逊相关系数、斯皮尔曼相关系数和肯德尔相关系数等。

皮尔逊相关系数适用于线性关系的测量，斯皮尔曼相关系数适用于非线性关系的测量，肯德尔相关系数适用于秩次相关的测量。

2. 相关性的解释：相关性指示两个序列之间的相似程度或相关程度。

相关系数介于-1和1之间，当相关系数接近1时，表示两个序列之间具有正相关关系，当相关系数接近-1时，表示两个序列之间具有负相关关系，当相关系数接近0时，表示两个序列之间没有线性相关关系。

3. 时间滞后相关性：序列之间的相关性可以是时滞相关的。

时间滞后相关性是指序列之间在时间上有一定的延迟，并且这种延迟有助于预测或解释。

例如，天气序列中的温度和降水量之间可能存在时间滞后相关性，即前一天的温度对当天的降水量有一定的影响。

4. 自相关和交叉相关：自相关是指一个序列与自身的相关性，交叉相关是指两个不同序列之间的相关性。

自相关可以用于检测序列中的周期性模式，交叉相关可以用于分析两个序列之间的相互关系。

5. 引导作用：序列相关性可以用于预测和引导。

通过分析序列之间的相关性，我们可以推断出一个序列对另一个序列的引导作用。

例如，股票市场中的相关性可以帮助我们预测某只股票的价格变动。

6. 噪声和趋势：序列相关性的解释需要考虑噪声和趋势。

噪声指的是序列中随机波动引起的不确定性，趋势指的是序列中的长期变化。

噪声和趋势可以对序列相关性的度量和解释产生影响。

7. 线性和非线性相关性：序列相关性可以是线性的或非线性的。

线性相关性表示两个序列之间存在着线性关系，可以用线性回归模型进行建模。

序列相关性

一、 序列相关性1. 经济理论指出，商品几口主要由进口国的经济发展水平，以及商品进口价格指数与国内价格指数对比因素决定。

由于无法取得中国商品进口价格指数，我们主要研究中国商品进口M 与国内生产总值GDP 的关系，数据见表4.2.1表4.2.1 1978—2001年中国商品进口与国内生产总值 年份 国内生产总值/亿元 商品进口/亿美元 年份 国内生产总值/亿元 商品进口/亿美元 1978 3624.1 108.9 1990 18547.9 533.5 1979 4038.2 156.7 1991 21617.8 637.9 1980 4517.8 200.2 1992 26638.1 805.9 1981 4862.4 220.2 1993 34634.4 1039.6 19825294.7 192.9 1994 46759.4 1156.1 1983 5934.5 213.9 1995 58478.1 1320.8 1984 7171 274.1 1996 67884.6 1388.3 1985 8964.4 422.5 1997 74462.6 1423.7 1986 10202.2 429.1 1998 78345.2 1402.4 1987 11962.5 432.1 1999 82067.46 1657 1988 14928.3 552.7 2000 89442.2 2250.9 198916909.2591.4200195933.32436.1用OLS 法建立中国商品进口方程，回归结果如下：对应的表达式为：ˆ194.840.02t tM GDP =+ (5.65) (18.12)20.945,0.942,110.33,0.375R R ESS DW ====进行序列相关性检验，作残差项e 与时间t以及t e 与1t e 的关系图，如下：t得到如下关系图：从上图可以看出，随即干扰项呈现正序列相关性。

计量经济学之序列相关性


H0 : 1 2 p 0
备择假设H为 1 （ H1：i i 1,2,, p） 中至少有一个不为零 若为真，则LM统计量在大样本下渐进 2 服从自由度为p的 分布：

LM nR ~
2
其中，n， （p）
2

R
2
分别是辅助回归方程（6）的样本容量和可决系 数
e e e e e e e e e e
t t t 1 t 1 t t 1 2 t 2 t 1 2 t
2 t 1
（3）
当n充分大时， et2 et21 有 et et 1 ˆ et2 所以
ˆ ˆ ˆ
(19)
三 自相关系数ρ的估计
广义差分法得以实施的关键是计算出自相关系数ρ的值，因此，必 须采用一些适当的方法对自回归系数ρ进行估计，通常适用的方法主 要有：经验法、利用 D.W.估计、科克伦-奥科特迭代法等。
下面我们着重介绍一下科克伦-奥科特迭代法： 科克伦-奥科特迭代法其实就是进行一系列的迭代，每一次迭代 都能得到比前一次更好的ρ的估计值。为了叙述方便，我们采用一元 回归模型来阐明这种方法， 多元回归模型下的迭代法与一元回归的原 理相同。 假设给定模型 Yt = β0 + β1 X t + μt 其中， μt = ρ1 μt−1 + ρ2 μt−2 + ⋯ + ρp μt−p + εt t=1+p,2+p,…,n (22) (21)
如果含有 k 个解释变量的多元回归模型（2）存在 p 阶序列相关 性，也可作类似变换，变换结果为
∗ Yt∗ = β0 1 − ρ1 − ⋯ − ρp + β1 X1t + β2 X∗ + ⋯ + βk X∗ + εt 2t kt ∗ 其中，Xit = Xit − ρ1 Xi(t−1) − ⋯ − ρp Xi(t−p)(i=1,2,…,p)。

序列相关性

序列相关性
序列相关性是统计学中的一个基本概念，它是指在一个序列中，前后两个元素之间可能存在的相互关系。

换句话说，如果前一个元素的变化对后一个元素的变化有影响，则可以说两个元素之间存在序列相关性。

序列相关性通常用来模拟某种可能的趋势，或者在数据集中确定某种特定的规律。

序列相关性可以在两个不同的元素之间用来检测潜在的相关性。

例如，如果两个实验组中，两个不同的元素在同一组中表现出相同的变化趋势，这就表明它们之间存在序列相关性。

从统计学的角度来看，可以通过确定序列相关性来判断实验结果是否具有可靠性。

序列相关性可以用来研究特定型号的趋势，以及判断某件事物在未来的特定时间段内的发展趋势。

考虑到每一次的变化 with the在实际的世界中都可能带来影响，序列相关性就可以作为研究趋势的基础，从而对未来可能发生的几率和变化描绘出一幅更清晰的图景。

此外，序列相关性还可以用来定义某种特定的模式。

例如，由于序列元素之间可能存在非常多的相互关系，因此可以判断某种特定的发展趋势。

同样的，序列相关性也可以用来检验数据集中的连续性，以便对因变量更有效的测量及预测。

序列相关性在统计学的很多方面都有重要的应用，它主要用来分析数据的相关性和预测趋势，以及判断某件事物在未来的特定时间段内的发展趋势。

考虑到序列元素之间可能存在许多复杂的关系，因此序列相关性可以用来模拟任何实际情况，从而提供有效的分析和预测。

《序列相关性》课件

《序列相关性》PPT课件
本PPT课件将介绍序列相关性的概念、应用和分析方法，帮助您深入理解序 列数据的特征和变化规律。
什么是序列及其应用
序列是一组有序的数据点，具有时间或者空间上的关联性。它在许多领域中有着广泛的应用，包括金融、气象、 生物学等。
序列相关性的介绍
序列相关性指的是序列中数据点之间的关联程度。了解序列相关性有助于我 们预测未来的趋势和进行有效的数据分析。
Ljung-Box检验的样本数据需要经过预处理，包括提取序列数据、计算自相关 系数以及计算统计量。
Ljung-Box检验的Python实现
使用Python中的statsmodels库可以方便地进行Ljung-Box检验，帮助我们分 析序列相关性。
Ljung-Box检验的R语言实现
R语言中的stats包提供了Ljung-Box检验的函数，可以用于检验序列数据的相关性和模型拟合程度。
3. Brockwell, P. J., & Davis, R. A. (2002). Introduction to time series and forecasting (2nd ed.). New York: Springer.
总结与答疑
通过本次课件的学习，希望您能够深入理解序列相关性的概念和应用，掌握 相关分析的方法和技巧，并能在实际问题中灵活运用。

自相关与偏相关在时间序列分 析中的应用
自相关和偏相关函数在时间序列分析中有着重要的应用，可以帮助我们识别 序列数据中的趋势、周期性和季节性。
序列相关性的局限性及其应对 方法
序列相关性分析存在一定的局限性，如不能区分因果关系等。为了克服这些 问题，我们可以结合其他方法进行综合分析。
序列相关性的应用场景和未来 发展

计量经济学 8 序列相关

Yi=0+1X1i+kXki+Yi-1+ui
（4）回归含有截距项
共五十六页
D.W. 统计(tǒngjì) 量:
杜宾和瓦森针对原假设：H0: =0， 即不存在(cúnzài)
一阶自回归，构如下造统计量：
共五十六页
当D.W.值在2左右(zuǒyòu)时，模型不存在一阶自相关。
证明： 展开(zhǎn kāi)D.W.统计量：
序列 相关 (xùliè)
Serial Correlation
共五十六页
一、序列相关的概念 二、序列相关的来源 三、序列相关的后果 四、序列相关的检验 五、序列相关的修正(xiūzhèng) 六、案例
共五十六页
一、序列(xùliè)相关的概念
对于(duìyú)模型
Yi=0+1X1i+2X2i+…+kXki+ui 随机项互不相关的基本假设表现为
避免产生虚假序列相关性的措施是在开始时建立一个 “一般”的模型，然后逐渐剔除确实不显著的变量。
共五十六页
六、案例(àn lì)
案例1：中国商品(shāngpǐn)进口模型
经济理论指出，商品进口主要由进口国的经济 发展(fāzhǎn)水平，以及商品进口价格指数与国内价格
指数对比因素决定的。 由于无法取得中国商品进口价格指数，我们主要研
但在模型设定中做了下述回归：
Yt=0+1X1t+ 1X2t + vt
因此， vt=3X3t + ut，如果X3确实影响Y，则出现序列
相关。
共五十六页
又如：如果(rúguǒ)真实的边际成本回归模型应为： Yt= 0+1Xt+2Xt2+ut
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

h
21
h
22
3、解析法
H
0
:
j
0 的 可能 性 较 大 ，
使某些原本显著的解释变量无法通过显著性检验。
因此，当随机误差项存在序列相关时，t 检验失去意义。
h
17
3、模型的预测功能失效
• 由于上述后果，使得模型不具有良好的统计性质。 所以，当模型出现序列相关性时，它的预测功能失 效。
h
18
三、序列相关性的检验
h
19
1、基本思路
则称为一阶序列相关，或自相关（autocorrelation）。
这是最常见的一种序列相关问题。
自相关往往可写成如下形式：
t t 1 t 1 1
其 中 ： 被 称 为 自 协 方 差 系 数 （ coefficient of autocovariance ） 或 一 阶 自 相 关 系 数 （ first-order coefficient of autocorrelation）。
2
一、序列相关性
h
3
1、序列相关的概念
对于模型
Y X X X i=1,2,…,n i 01 1 i 22 i kkii
随机误差项互相独立的基本假设表现为：
Co(v,)0
ij
如果出现
i≠j，i,j=1,2,…,n
Co(v,)0
ij
i≠j，i,j=1,2,…,n
即对于不同的样本点，随机误差项之间不再是不相关的，而 是存在某种相关性，则认为存在序列相关。
序列相关性 Serial Correlation
一、序列相关性的概念 二、序列相关性的后果 三、序列相关性的检验 四、具有序列相关性模型的估计 五、案例
h
1
普通最小二乘法（OLS）要求计量模型 的随机误差项相互独立或序列不相关。
如果模型的随机误差项违背了互相独立 的基本假设，则认为存在序列相关。
h
E
21
2
E
n1
E
n2
2
1
12
1n
n
E
2
1
2
2
Байду номын сангаас
2
n
n 1
n2
2
n
E
1n
2
1
E
12
E
2n
E
21
2
2
E 2 n
E
n1
E
n2
E
1n
E
2n
2
n
E
1n
E
2n
2
2
2
h
6
如果仅存在
E(ii1)0 （i=1,2,…,n-1）
h
12
(5)数据的“编造”
例如：如果季度数据来自月度数据的简单平 均，那么这种平均的计算会减弱每月数据的波动 而使季度数据更为平滑，从而使随机干扰项出现 序列相关。
此外，当历史数据缺失时，在两个时间点之 间采用“内插”技术，也可能导致随机干扰项出 现序列相关。
h
13
二、序列相关性的后果
h
14
1、参数估计量非有效
h
4
在其他基本假设仍满足的条件下，随机误差项序列 相关意味着：
E( )0 （i≠j，i,j=1,2,…,n）
ij
h
5
如果用矩阵符号表示，则序列相关意味着：
1
E ( N N
)
E
2
1
2
n
E 2
1
E
12
E
21
E 2
2
E
n1
E
n2
2
E 12
于是在猪肉价格影响牛肉消费量的情况下，这种模 型设定的偏误往往导致随机误差项中有一个重要的系 统性影响因素，使其呈序列相关性。
h
10
(3)设定误差：不正确的函数形式
例如：如果边际成本模型应为：
Yt= 0+1Xt+2Xt2+t 其中：Y=边际成本，X=产出。
但在建模时误将模型设定为：
Yt= 0+1Xt+vt 因此，由于 vt= 2Xt2+t ，包含了产出的平方对随 机误差项的系统性影响，随机误差项也呈现序列相 关性。
• OLS参数估计量仍具无偏性
• OLS估计量不具有有效性 • 在大样本情况下，参数估计量仍然不具有渐近有 效性，这就是说参数估计量不具有一致性
因为在有效性的证明过程中利用了 E() 2I
即同方差性和互相独立性条件。
h
15
2、变量的显著性检验失去意义
在变量的显著性检验中，构造了t统计量，该统计量 服从自由度为(n-k-1)的t分布。这些只有当随机误差 项具有同方差和互相独立时才能成立。
h
16
如果出现了序列相关，即
i
和 j 相关，那么
Y和
i
Y 不再独立，
j
从而无法导出：
ˆ j
~
N(
j
,
2
c
jj
)
、
e e
2
~
c 2 (n k 1) 及
t
分
布统计量；
此外，如果出现了序列相关，那么 参数估计量不具有有效性，
参数估计量的方差（从而标准差）将较大，计算得到的 t 统
计量值将较小，从而接受原假设
h
11
(4)蛛网现象
例如：农产品供给对价格的反映本身存在一个
滞后期：Qt= 0+1Pt-1+t
其中：Qt=t 年农产品的供给;
Pt-1= t-1 年农产品的价格。
意思是，农民由于在前一年度（t-1）的过量生
产（使该期价格下降）很可能导致在下一年度（t）
削减产量，因此不能期望随机干扰项是随机的，往
往产生一种蛛网模式。
• 序列相关性检验方法有多种，但基本思路是相 同的：
• 首先，采用普通最小二乘法估计模型，以求得 随机误差项的“近似估计量”
e~Y(Yˆ)
i i i 0ls
• 然后，通过分析这些“近似估计量”之间的相关 性，以达到判断随机误差项是否具有序列相关 性的目的。
h
20
2、图示法
由于残差 e~i 可以作为 i 的估计，因此如果 i 存在序列相关，必然会由残差项 e~i 反映出来， 因此可利用 e~i 的变化图形来判断随机项的序 列相关性。
h
7
2、序列相关产生的原因
（1）惯性 （2）设定误差：模型中遗漏了显著的变量 （3）设定误差：不正确的函数形式 （4）蛛网现象 （5）数据的“编造”
h
8
（1）惯性
大多数经济时间数据都有一个明显的 特点，就是它的惯性。
GDP、价格指数、生产、就业与失业 等时间序列都呈周期性，如周期中的复苏 阶段，大多数经济序列均呈上升趋势，序 列在每一时刻的值都高于前一时刻的值， 似乎有一种内在的动力驱使这一势头继续 下去，直至某些情况（如利率或课税的升 高）出现才把它拖慢下来。
h
9
（2）设定误差：模型中遗漏了显著的变 量
例如：如果对牛肉需求的正确模型应为
Yt=0+1X1t+2X2t+3X3t+t 其中：Y=牛肉需求量，X1=牛肉价格，X2=消费者收入， X3=猪肉价格。
但在建模时误将模型设定为：
Yt= 0+1X1t+2X2t+vt 那么该式中的随机误差项实际上是：vt= 3X3t+t,