阿氏圆 (1)

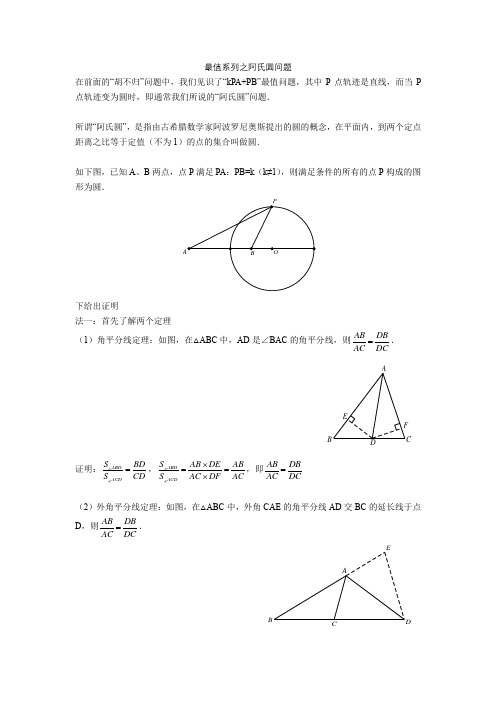
最值系列之阿氏圆问题在前面的“胡不归”问题中，我们见识了“kPA+PB”最值问题，其中P 点轨迹是直线，而当P 点轨迹变为圆时，即通常我们所说的“阿氏圆”问题．所谓“阿氏圆”，是指由古希腊数学家阿波罗尼奥斯提出的圆的概念，在平面内，到两个定点距离之比等于定值（不为1）的点的集合叫做圆．如下图，已知A 、B 两点，点P 满足PA ：PB=k （k≠1），则满足条件的所有的点P 构成的图形为圆．下给出证明法一：首先了解两个定理（1）角平分线定理：如图，在△ABC 中，AD 是∠BAC 的角平分线，则AB DBAC DC=．证明：ABD ACDS BD SCD =，ABD ACDS AB DE AB SAC DF AC ⨯==⨯，即AB DBAC DC=（2）外角平分线定理：如图，在△ABC 中，外角CAE 的角平分线AD 交BC 的延长线于点D ，则AB DBAC DC=．FEDCBAABCDE证明：在BA 延长线上取点E 使得AE=AC ，连接BD ，则△ACD ≌△AED （SAS ），CD=ED 且AD 平分∠BDE ，则DB AB DE AE =，即AB DBAC DC=．接下来开始证明步骤：如图，PA ：PB=k ，作∠APB 的角平分线交AB 于M 点，根据角平分线定理，MA PAk MB PB==，故M 点为定点，即∠APB 的角平分线交AB 于定点；作∠APB 外角平分线交直线AB 于N 点，根据外角平分线定理，NA PAk NB PB==，故N 点为定点，即∠APB 外角平分线交直线AB 于定点；又∠MPN=90°，定边对定角，故P 点轨迹是以MN 为直径的圆．法二：建系不妨将点A 、B 两点置于x 轴上且关于原点对称，设A （-m ，0），则B （m ，0），设P （x ，y ），PA=kPB ，即：()()()()()()22222222222222222122102201x m y k x m k y kx y m k m x k m m k mx y x m k ++=-+-+-++-=++-+=-解析式满足圆的一般方程，故P 点所构成的图形是圆，且圆心与AB 共线．那么这个玩意和最值有什么关系呢？且来先看个例子：如图，在Rt △ABC 中，∠C=90°，AC=4，BC=3，以点C 为圆心，2为半径作圆C ，分别交AC 、BC 于D 、E 两点，点P 是圆C 上一个动点，则12PA PB 的最小值为__________．【分析】这个问题最大的难点在于转化12PA ，此处P 点轨迹是圆，故转化方法与之前有所不同，如下，提供两种思路．法一：构造相似三角形注意到圆C 半径为2，CA=4，连接CP ，构造包含线段AP 的△CPA ，在CA 边上取点M 使得CM=2，连接PM ，可得△CPA ∽△CMP ，故PA ：PM=2:1，即PM=12PA ．问题转化为PM+PB 最小值，直接连BM 即可．【问题剖析】（1）这里为什么是12PA ？答：因为圆C 半径为2，CA=4，比值是1:2，所以构造的是12PA ，也只能构造12PA ．EABC DP（2）如果问题设计为PA+kPB 最小值，k 应为多少？ 答：根据圆C 半径与CB 之比为2:3，k 应为23．【小结】此类问题都是构造好的图形搭配恰当的比例，构造相似转化线段即可解决．法二：阿氏圆模型对比一下这个题目的条件，P 点轨迹是圆，A 是定点，我们需要找出另一个定点M 使得PM:PA=1:2，这不就是把“阿氏圆”的条件与结论互换了一下嘛！而且这种问题里，给定的圆的位置、定点A 的位置、线段的比例等，往往都是搭配好的！P 点轨迹圆的圆心C 点和A 点在直线AC 上，故所求M 点在AC 边上，考虑到PM ：PA=1:2，不妨让P 点与D 点重合，此时DM=12DA =1，即可确定M 点位置．如果对这个结果不是很放心，不妨再取个特殊的位置检验一下，如下图，此时PM=3，PA=6，亦满足PM:PA=1:2．【小结】法二其实是开了上帝视角，在已知其是阿氏圆的前提下，通过特殊点找出所求M 点位置，虽不够严谨，却很实用．已知PA 、圆确定PB已知PA 、PB 之比确定圆【练习1】如图，在ABC ∆中，∠ACB=90°，BC=12，AC=9，以点C 为圆心，6为半径的圆上有一个动点D ．连接AD 、BD 、CD ，则2AD+3BD 的最小值是 ．【分析】首先对问题作变式2AD+3BD=233AD BD ⎛⎫+ ⎪⎝⎭，故求23AD BD +最小值即可．考虑到D 点轨迹是圆，A 是定点，且要求构造23AD ，条件已经足够明显．当D 点运动到AC 边时，DA=3，此时在线段CD 上取点M 使得DM=2，则在点D 运动过程中，始终存在23DM DA =．问题转化为DM+DB 的最小值，直接连接BM ，BM 长度的3倍即为本题答案．ABCD【练习2】如图，已知正方ABCD 的边长为4，圆B 的半径为2，点P 是圆B 上的一个动点，则12PD PC 的最大值为_______．【分析】当P 点运动到BC 边上时，此时PC=2，根据题意要求构造12PC ，在BC 上取M使得此时PM=1，则在点P 运动的任意时刻，均有PM=12PC ，从而将问题转化为求PD -PM的最大值．连接PD ，对于△PDM ，PD -PM ＜DM ，故当D 、M 、P 共线时，PD -PM=DM 为最大值．AB CDP。

阿氏圆最值问题阿氏圆又称阿波罗尼斯圆，已知平面上两点A 、B ，则所有满足PAk PB=（0k >且k 不等于1）的点P 的轨迹是一个圆，这个轨迹最先由古希腊数学家阿波罗尼斯发现，故称阿氏圆例1、问题提出：如图1，在Rt △ABC 中，∠ACB ＝90°，CB ＝4，CA ＝6，⊙C 半径为2，P 为圆上一动点，连结AP 、BP ，求AP ＋12BP 的最小值．尝试解决：为了解决这个问题，下面给出一种解题思路：如图2，连接CP ，在CB 上取点D ，使CD ＝1，则有CD CP ＝CP CB ＝12，又∵∠PCD ＝∠BCP ，∴△PCD ∽△BCP ，∴PD BP ＝12，∴PD ＝12BP ，∴AP ＋12BP ＝AP ＋P D ． 请你完成余下的思考，并直接写出答案：AP ＋12BP 的最小值为 ．自主探索：在“问题提出”的条件不变的情况下， 13AP ＋BP 的最小值为 ．拓展延伸：已知扇形COD 中，∠COD ＝90º，OC ＝6，OA ＝3，OB ＝5，点P 是 ⌒CD 上一点，求2P A ＋PB 的最小值．例2、问题背景 如图1，在△ABC 中，BC ＝4，AB ＝2AC问题初探 请写出任意一对满足条件的AB 和AC 的值：AB ＝__________，AC ＝___________． 问题再探 如图2，在AC 右侧作∠CAD ＝∠B ，交BC 的延长线于点D ，求CD 的长． 问题解决 求△ABC 面积的最大值．向内构造类型DCBACBA 图2图1BDCA2、如图，四边形ABCD 为边长为4的正方形，B 的半径为2，P 是B 上一动点，则12PD PC +的最小值为_________+4PC 的最小值为_________．3、如图，已知菱形ABCD 的边长为4，=60B ο∠，B 的半径为2，P 为B 上一动点，则1+2PD PC 的最小值为________4、如图，点C 坐标为（2，5），点A 的坐标为（7，0），CB 在C 上一动点，OB AB 的最小值为___________P D CBAPDCB ADCP BA5、如图， AB 为O 的直径，AB ＝2，点C 与点D 在AB 的同侧，且AD ⊥AB ，BC ⊥AB ，AD ＝1，BC ＝3，点P 是OPC +的最小值为________6、在ABC ∆中，=9860AB BC ABC ο=∠=，，，A 的半径为6，P 是A 上的动点，连接PB PC 、，则 32PC PB +的最小值为___________7、如图，边长为4的正方形，内切圆记为O ，P 是O+PB 的最小值为_________BPC BA8、如图，菱形ABCD 的边长为2，∠ABC ＝ 60o ，A 与BC 相切于点E ，点P 是A 上一动点，PB +的最小值为_________9、如图，在Rt ABC 中，30A ∠=︒， 8AC =，以C 为圆心，4为半径作⊙C ． （1）试判断⊙C 与AB 的位置关系，并说明理由;（2）点F 是⊙C 上一动点，点D 在AC 上且2CD =，试说明FCD ACF ; （3）点E 是AB 边上任意一点，在（2）的情况下，试求出12EF FA +的最小值．E DCB APFEADCB10、如图1，抛物线y＝ax2＋（a＋3）x＋3（a≠0）与x轴交于点A（4，0），与y轴交于点B，在x轴上有一动点E（m，0）（0＜m＜4），过点E作x轴的垂线交直线AB于点N，交抛物线于点P，过点P作PM⊥AB于点M．（1）求a的值和直线AB的函数表达式；（2）设△PMN的周长为C1，△AEN的周长为C2，若＝，求m的值；（3）如图2，在（2）条件下，将线段OE绕点O逆时针旋转得到OE′，旋转角为α（0°＜α＜90°），连接E′A、E′B，求E′A＋E′B的最小值．11、如图，抛物线y＝﹣x2＋bx＋c与直线AB交于A（﹣4，﹣4），B（0，4）两点，直线AC：y＝﹣x﹣6交y轴于点C．点E是直线AB上的动点，过点E作EF⊥x轴交AC于点F，交抛物线于点G．（1）求抛物线y＝﹣x2＋bx＋c的表达式；（2）连接GB，EO，当四边形GEOB是平行四边形时，求点G的坐标；（3）①在y轴上存在一点H，连接EH，HF，当点E运动到什么位置时，以A，E，F，H 为顶点的四边形是矩形？求出此时点E，H的坐标；②在①的前提下，以点E为圆心，EH长为半径作圆，点M为⊙E上一动点，求AM＋CM 它的最小值．向外构造类型1、如图，点A 、B 在O 上，OA ⊥OB ， OA ＝OB ＝12，点C 是OA 的中点，点D 在OB 上， OD ＝10．点P 是O 上一动点，则12PC PD +的最小值为_________2、如图，在扇形CAB 中，CA ＝4， 120CAB ∠= ，D 为CA 的中点，P 为BC ˆ上一动点（不与C ，B 重合），则2PD ＋PB 的最小值为（ ）A．4+ B． C ．16 D．43、如图O 的半径为2，AB 为直径。

阿氏圆专题知识点回顾：轨迹为圆的几何条件：一、一动点到一定点的距离不变，此动点的轨迹为圆； 二、定角对定长，也叫“隐形圆”注意：1、定长表示线段的长度和位置不变；2、定角为90°，角的顶点的轨迹为圆，定角不为90°，角的顶点的轨迹为一段圆弧；阿氏圆定义：已知平面两个定点A 、B 到一动点P 的比值为一定值k （k ≠1），那么这个动点P 的轨迹是一个圆。

注意：1、此圆与直线AB 交于点E 和点F ，点E 以定比内分线段AB,点F 以定比外分线段AB;2、k=1,此动点在定线段的垂直平分线上。

图文：EBFPOABPAK PB PA =,且K EB EA FB FA == 1==K PBPA解题思路：1、连接动点至圆心，即连接OP ，再连接其中一个定点于圆心，即连接OB,为了确定另一个定点也在直线OB 上;2、计算OB 和OP 的长度，确定比值OBOP=K; 3、在OB 上取一点，A ，使OP OA =OBOP=K,得三角形相似即△POA ∽△BOP ； 4、根据△POA ∽△BOP ，可得PA=K ·PB,可将PB 和PA 进行转换。

阿氏圆总结：遇到”“kPB PA +型的最值问题，要将系数为K 的线段转化为系数为1的线段，即要考虑”“PC kPB =。

求kAB PA +可转化为PA+PC.图1 图2 图3 关键在于确定点C 的位置，当点A 、P 、C 三点共线时，PA+PC.最小，即PA+k ·PB 值最小。

（提示：kAB PA +=k （k 1PA+PB ）,所以也可以将k1PA 转化为系数为1的线段。

）B APOBC APOBC PPAO相关例题：例1、如图，点A 、B 在圆O 上，且OA=OB=6，且OA ⊥OB ，点C 是OA 的中点，点D 在OB 上，且0D=4，动点P 在圆O 上，则2PC+PD 的最小值为 。

解题思路：连接OP,圆上一动点P ，OA 上有一定点C ，由阿氏圆可得，直线OA 上肯定存在另一定点E ，使得PE PC 为定值。

关于阿氏圆解决最值问题的一些认识
B A P 一．对阿氏圆这个知识的认识：
已知平面上两点A 、B ，则所有满足PA ：PB= k (K ≠1)的点P 的轨迹是一个以定比m ：n 内分和外分定线段AB 的两个分点的连线为直径的圆，这个轨迹最先由古希腊数学家阿波罗尼斯发现，又称阿波罗尼斯圆，简称阿氏圆（k=m ：n ）
1. 两定点已知，动点P 所在的圆是所探求的结论，未知，可以画出来。

2. 要画出这个圆，须在AB 上找到一点M ，使得AM ：BM=k,
在AB 的延长线上找一点N ，使得AN:MN=K, 以MN 为直径画出动点P 所在的圆，圆心O ，两定点A,B 共线，圆心O 在两定点右侧。

3. 连接PO ，则?PBO 相似于?PAO,从而发现了斜A 型相似的基本图形。

观察它的构成，为后面问题的解答做好铺垫。

二．对利用阿氏圆知识解决的最值问题的认识：
例：如图，在Rt △ABC 中，∠ACB ＝90°，CB ＝4，CA ＝6，⊙C 的半径为2，P 为圆上一动
点，连接AP ，BP ，求AP ＋12
BP 的最小值．
1.在求解的问题中，动点所在的阿氏圆已知，阿氏圆中的k 值已知（即所求问题中的非1系数），阿氏圆中的两定点知其一，系数非1的乘积中，动线段的定端点就是该定点，我们需要找到另一个定点。

2.要找到另一个定点，就必须构造斜A 相似图形，观察一的内容，明确做法：连接PC(C 为圆心），作∠CPD=∠CBP 交BC 于点D ，点D 即为阿氏圆中的另一个定点。

根据相似，可得出12BP=PD ，所以AP+12
BP=AP+PD,当A,P,D 三点共线时，取得最小值。

【模型导学】利用阿氏圆模型快速求解最值问题阿氏圆最值模型
在前面的“胡不归”问题中，我们见识了“kPA+PB”最值问题，其中P点轨迹是直线，而当P点轨迹变为圆时，即通常我们所说的“阿氏圆”问题．
【模型来源】
“阿氏圆”又称为“阿波罗尼斯圆”，如下图，已知A、B两点，点P满足PA：PB=k（k≠1），则满足条件的所有的点P的轨迹构成的图形为圆．这个轨迹最早由古希腊数学家阿波罗尼斯发现，故称“阿氏圆”.
阿氏圆最值模型例题讲解
阿氏圆最值模型小试牛刀
以上内容选自王通博初中数学
长按解锁
好书推荐
《16项快速提分黑科技（中考数学）》，即在学生的数学知识、数学技能、数学思想和方法等水平一定，学习时间紧迫、学习成绩徘徊不前的情况下，教给学生作者近三十年总结的最优化、最有效、最系统、最全面、最深入的16项一级“黑科技”、121个二级“黑科技”，曝光不会也能得分的提分秘籍!如果学生能迅速掌握这些方法、策略和技术等“黑科技”，便能最大限度帮助学生快速提分，在关系自己前途的考试中取得新的突破，这不仅能帮助学生提高分数，而且还能帮助学生树立学好数学的信心，对于后续的学习具有深刻的启发与指导意义。

黑科技提分技术最全！新！快！最有效！
点击抢购。

阿波罗尼斯圆是什么。

？阿波罗尼斯（Apollonius）圆，简称阿⽒圆。

[编辑本段]定义 在平⾯上给定相异两点A、B，设P点在同⼀平⾯上且满⾜PA/PB= λ，当λ>0且λ≠1时，P点的轨迹是个圆，这个圆我们称作阿波罗尼斯圆。

这个结论称作阿波罗尼斯轨迹定理。

设M、N分别为线段AB按定⽐λ分割的内分点和外分点，则MN为阿波罗尼斯圆的直径，且MN=［２λ／（λ^2-1）］AB。

[编辑本段]证明 我们可以通过公式推导出AN的长度：AN:BN＝AP:BP ，其中BN=AN+AB，所以AN:(AN+AB)＝AP:BP=>AN=AP×AB÷(BP-AP)，以NP为直径的圆就是我们所求的轨迹圆。

[编辑本段]性质 由阿波罗尼斯圆可得阿波罗尼斯定理，即： 设三⾓形的三边和三中线分别为a、b、c、ma(a为下标，下同）、mb、mc，则有以下关系： b^2+c^2=a^2/2+2ma^2； c^2+a^2=b^2/2+2mb^2； a^2+b^2=c^2/2+2mc^2。

阿波罗尼斯圆：⼀动点P与两定点A、B的距离之⽐等于定⽐m：n，则点P的轨迹，是以定⽐m：n内分和外分定线段的两个分点的连线为直径的圆。

这个轨迹最先由古希腊数学家阿波罗尼斯发现，故称阿⽒圆。

这个定理的证明⽅法很多。

下⾯是笔者的分析与证明，希望读者喜欢。

如图，P是平⾯上⼀动点，A、B是两定点，PA∶PB＝ m∶n ，M是AB的内分点（M在线段AB上），N是AB的外分点（N在AB的延长线上）且AM∶MB＝AN∶NB＝m∶n，则P点的轨迹是以MN为直径的圆。

下⾯先证明两个定理：⼀、如图⼀，已知M是BC上⼀点，且AB∶AC＝BM∶MC，求证：AM平分∠BAC（三⾓形内⾓平分线定理的逆定理）证明：过C点作CD∥AM交BA的延长线于D，则AB∶AD＝BM∶MC∵AB∶AC＝BM∶MC，∴AB∶AD ＝AB∶AC，∴AC＝AD，∴∠D＝∠3，∵CD∥AM，∴∠1＝∠D，∠2＝∠3，∴∠1＝∠2，∴AM平分∠BAC。

阿氏圆知识点总结1. 定义和特点阿氏圆是一种特殊类型的圆，它可用来解决一些几何问题。

与普通的圆不同，阿氏圆的圆周上的任何一段圆弧都与圆心之外一点的连线成一个特定的恒定角度。

在阿氏圆内，存在两个特定的点，一个是内圆心，一个是外圆心。

这两个点与圆上的任意一点连成的线段呈现出恒定的夹角。

这些特点使得阿氏圆在数学和工程领域有着广泛的应用。

2. 阿氏圆的历史阿氏圆是由17世纪的意大利数学家乔万尼·贝尔努利所提出的。

他的研究成果被认为是建立了航空学的良好基础，为后来的飞行器设计和控制系统提供了有力支持。

阿氏圆之所以被命名为“阿氏”是因为乔万尼·贝尔努利的英文名是“Giovanni Alfonso”而被称为“Giovanni Alfonso”.3. 构造方法阿氏圆的构造方法有多种，其中最常见的是利用平行直线和圆相交的关系来构造。

具体方法如下：- Step 1：在平面上选择一条直线作为基准线。

- Step 2：在基准线上选择一个点作为内圆心。

- Step 3：从内圆心开始画一条半直线，使得它和基准线成一个特定的角度。

- Step 4：通过内圆心，将这条半直线上每一个点与基准线的交点作为初始圆上的一个点。

- Step 5：连接初始圆上的点和内圆心，得到阿氏圆。

4. 基本性质阿氏圆是一种精美的几何图形，它具有许多基本性质，其中最为重要的包括以下几点：- 周长和半径：由于阿氏圆上的任意一段弧都与外圆心的连线成一个特定的角度，因此，圆周上的每一小段都是等长的。

此外，阿氏圆的半径大小也是不固定的，但是半径越大，圆周上的弧长越大。

- 角度恒定性：阿氏圆上任何一条弧都与外圆心的连线成一个恒定的角度。

这个角度也被称为阿氏角，它在阿氏圆上是始终不变的。

5. 应用领域阿氏圆由于其独特的特点，被广泛应用于航空航天、船舶和汽车制造、导弹制导系统、机械制造等领域。

在飞机设计中，利用阿氏圆可精确控制机体的姿态，提高飞行性能和飞行安全。

定义：已知平面上两点A,B,则所有满足PA/PB=k且不等于1的点P的轨迹是一个圆，这个轨迹最先由古希腊数学家阿波罗尼斯发现，具体的描述：一动点P到两定点A、B的距离之比等于定比m：n，则P点的轨迹，是以定比m：n内分和外分定线段AB的两个分点的连线为直径的圆。

该圆称为阿波罗尼斯圆，简称阿氏圆。

解题策略：利用两边成比例且夹角相等构造相似三角形（简称美人鱼相似）“阿氏圆”一般解题步骤第一步:连接动点至圆心0(将系数不为1的线段的两个端点分别与圆心相连接),则连接0P、OB;第二步:计算出所连接的这两条线段OP、OB长度;第三步:计算这两条线段长度的比=k;第四步:在0B上取点C,使得;第五步:连接AC,与圆0交点即为点P.阿氏圆最值问题例题精讲例1:问题提出:如图1,在R△ABC中,∠ACB=90,CB=4,AC=6.圆C半经为2,P为圆上一助点,连结AP,BP,求AP+BP的最小值尝试解决：为了解块这个间题,下面给出一种解题思路、如图2,连接CP,在CB上取点D,使CD=1则有,又∵∠PCD=∠BCP,∴△PCD△BCP,∴，∴PD=,∴AP+AP+PD请你完成余下的思考,并直接写出答案:AP+BP的最小值为。

自主探索:在“间题提出”的条件不变的情况下,AP+BP的最小值为。

拓展延伸:已知扇形COD中,∠COD=90,0C=6,OA=3,0B=5,点P是弧CD上一点,求2A+PB的最小值。

强化训练向内构造类型1,如图,已知AC=6,BC=8,AB=10,圆C的半经为4,点D是圆C上的动点,连接AD、BD,则AD+BD的最小值为。

2.在Rt△ABC中,∠ACB=90°AC=4,BC=3,点D为△ABC内一动点,且满足CD=2，则AD+BD的最小值为。

3、如图,在R△ABC中,∠C=90°,CA=3,CB=4.⊙C的半径为2,点P是⊙C上一动点,则AP+PB的最小值为。

4、如图,四边形ABCD为边长为4的正方形, ⊙B的半径为2,P是⊙B上一动点,则PD+PC的最小值为。

专题阿氏圆定义平面内到两个定点,A B 的距离之比为定值()1≠K K 的点的轨迹是圆证明：令B 为坐标原点，A 的坐标为(a,0).则动点P(x,y)1．（2017·武汉六校联考）阿波罗尼斯是古希腊著名数学家，与欧几里得、阿基米德被称为亚历山大时期数学三巨匠，他对圆锥曲线有深刻而系统的研究，主要研究成果击中在他的代表作《圆锥曲线》一书，阿波罗尼斯圆是他的研究成果之一，指的是：已知动点M 与两定点A 、B 的距离之比为λ（0λ>，1λ≠），那么点M 的轨迹就是阿波罗尼斯圆．下面，我们来研究与此相关的一个问题．已知圆：221x y +=和点1(,0)2A -，点(1,1)B ，M 为圆O 上动点，则2||||MA MB +的最小值为（）A ．6B ．7C ．10D ．112．（2020·肥城市第一高级中学高三月考）古希腊著名数学家阿波罗尼斯与欧几里得、阿基米德齐名.他发现:“平面内到两个定点,A B 的距离之比为定值()1λλ≠的点的轨迹是圆”.后来,人们将这个圆以他的名字命名,称为阿波罗尼斯圆,简称阿氏圆在平面直角坐标系xOy 中,()()2,0,4,0,A B -点12PA P PB =满足.设点P 的轨迹为C ,下列结论正确的是（）A ．C 的方程为()2249x y ++=B ．在x 轴上存在异于,A B 的两定点,D E ,使得12PD PE =C ．当,,A B P 三点不共线时,射线PO 是APB ∠的平分线D ．在C 上存在点M ,使得2||MO MA =3．（2020·浙江省温岭中学高三一模）已知()2,0A -，()2,0B ，动点M 满足2MA MB =，则点M 的轨迹方程是___________；又若0MA MB ⋅=，此时MAB △的面积为___________.4．（2019·湖北省孝感高中高二月考）公元前3世纪，古希腊数学家阿波罗尼斯（Apollonius ）在《平面轨迹》一书中，曾研究了众多的平面轨迹问题，其中有如下结果：平面内到两定点距离之比等于已知数的动点轨迹为直线或圆.后世把这种圆称之为阿波罗尼斯圆.已知直角坐标系中(2,0),(2,0)A B -，则满足||2||PA PB =的点P 的轨迹的圆心为____________，面积为____________.5．（2020·湖南省高三期末（文））阿波罗尼斯与阿基米德、欧几里得被称为亚历山大时期数学三巨匠．“阿波罗尼斯圆”是他的代表成果之一：平面上一点P 到两定点,A B 的距离之满足||(01)||PA t t t PB =>≠且为常数，则P 点的轨迹为圆．已知圆O ：221x y +=和1(,0)2A -，若定点(,0)B b （12b ≠-）和常数λ满足：对圆O 上任意一点M ，都有||||MB MA λ=，则=λ_________，=b ___________.5．（2019·浙江省高二期末）公元前3世纪，古希腊数学家阿波罗尼斯在前人的基础上写了一部划时代的著作《圆锥曲线论》，该书给出了当时数学家们所研究的六大轨迹问题，其中之一便是“到两个定点的距离之比等于不为1的常数的轨迹是圆”，简称“阿氏圆”．用解析几何方法解决“到两个定点(00)O ，，(30)A ，的距离之比为12的动点M 轨迹方程是：22230x y x ++-=”，则该“阿氏圆”的圆心坐标是______，半径是_____．6．（2020·江西省高二期末（文））阿波罗尼斯（约公元前262-190年）证明过这样一个命题：平面内到两定点距离之比为常数()0,1k k k >≠的点的轨迹是圆，后人将这个圆称为阿氏圆.若平面内两定点A B 、间的距离为2，动点P 满足3PA PB=，当,,P A B 不共线时，三角形PAB 面积的最大值是_______________.8．（2019·安徽省高二月考（理））若平面内动点P 到两定点,A B 的距离之比||||PA PB λ=（其中λ为常数，0,1λλ>≠）,则动点P 的轨迹为圆，这个轨迹最先由古希腊数学家阿波罗尼斯发现的，故称作阿波罗尼斯圆.若已知(1,0),(1,0),2A B λ-=,则此阿波罗尼斯圆的方程为_____.9．（2020·福建省高三月考（理））波罗尼斯（古希腊数学家，约公元前262-190年）的著作《圆锥曲线论》是古代世界光辉的科学成果，它将圆锥曲线的性质网罗殆尽几乎使后人没有插足的余地.他证明过这样一个命题：平面内与两定点距离的比为常数k （0k >且0k ≠）的点的轨迹是圆，后人将这个圆称为阿波罗尼斯圆.现有ABC ∆，4,sin 2sin AC C A ==，则当ABC ∆的面积最大时，AC 边上的高为_______________.10．（2020·湖北襄阳四中高二期末）一动点到两定点距离的比值为非零常数λ，当1λ≠时，动点的轨迹为圆，后世称之为阿波罗尼斯圆已知两定点A 、B 的坐标分别为：()4,0A 、()10B ,，动点M 满足2AM BM =．（1）求动点M 的阿波罗尼斯圆的方程；（2）过()2,3P 作该圆的切线l ，求l 的方程．11．（2019·湖北省高二期中）阿波罗尼斯（约公元前262-190年）证明过这样一个命题：平面内到两定点距离之比为常数(0,1)k k k >≠的点的轨迹是圆，后人将这个圆称为阿波罗尼斯圆.若平面内两定点0,0,()()3,0O A ，动点P 满足12PO PA =.（1）求点P 的轨迹方程；（2）求22PO PA +的最大值.12．（2018·黑龙江省高一期末）平面内动点P 到两定点A ，B 距离之比为常数(0,1)λλλ>≠，则动点P 的轨迹叫做阿波罗尼斯圆.现已知定点()0,0A 、()6,0B -，圆心为C ，（1）求满足上述定义的圆C 的方程，并指出圆心C 的坐标和半径；（2）若12λ=，且经过点()4,2Q 的直线l 交圆C 于M ，N 两点，当CMN ∆的面积最大时，求直线l 的方程.7专题阿氏圆参考答案1．C2．BC3．223320120x y x +-+=；165.4．10,03⎛⎫ ⎪⎝⎭649π5．2λ=2b =-6．(1,0)-27．348．2210103x y x +-+=9．8310．（1）224x y +=；（2）2x =或12590x y -+=．11．（1）22(1)4x y ++=；（2）45.12．（2）60x y +-=.。

《阿氏圆习题课》课堂实录及教学启示摘要:以阿氏圆习题为例,带领学生回归教材,从教材中寻找解题方法,并进行深度思考,探讨如何运用教材进行有效的复习备考,从而更好地对接新高考,达到立德树人的育人目标. 关键词:阿氏圆;回归教材;复习备考一、引言新高考实施以来,如何更好地以新教材为载体进行复习备考,成为摆在一线教师面前的重大课题.近几年的高考试题,呈现一个显著特点,即从教材例题,习题进行深度的改编.因此,新教材的例题是高考复习备考的重要依据.以一道阿氏圆试题为例,阐述如何于课堂教学中引导学生应用新教材例题进行复习备考,探索使用新教材对接新高考的方式方法. 二、课堂实录1.试题呈现,初步求解湖北省鄂东南教改联盟2024高三期中联考第8题在ABC ∆中,2AB AC =,ABC ∆的面积为1,则BC 的最小值为 师：本题以三角形为载体考查学生是否掌握运用正弦定理,余弦定理等解决三角形问题.由于要求线段的最小值,常规解法是将线段BC 表示成某一个变量的函数关系,再借助函数求最值的方法求出最小值. 生:独立思考并给出解法设AC x =,2AB x =,BAC θ∠=,则12sin 12x x θ⋅⋅⋅=,即21sin x θ=. 在ABC ∆中,由余弦定理可得22254cos BC x x θ=-54cos sin θθ-=令54cos sin y θθ-=,则()2sin 16yθϕ+=+,25116y≤+,所以3y ≥,则3BC ≥从而BC 3【设计意图】抛出例题,学生独立思考,借助三角形的相关性质定理解决问题.此时学生虽然初步解决了问题,但是思维停留在静态,无法进一步提升思维,达不到深度课堂的要求. 2.引发认知冲突,回归课本师:在上述解法中,我们在ABC ∆中借助余弦定理和面积公式解决问题,将线段BC 表示成BAC θ∠=的函数,再运用三角函数的知识求出最小值.同学们可否换个角度思考问题：从运动变化的观点思考？ 生(众):思考….师:引导学生回顾湘教版数学选择性必修第一册第2.7节例2到两个定点A ,B 的距离之比为定值()0λλ>的所有的点组成什么形状的曲线？解:以B 为原点,建立平面直角坐标系.()0,0B ,(),0A a ,其中a AB =.设(),P x y 是平面上任意一点,由PAPBλ=,得()2222x a y x yλ-+=+,化简得()()222221120x yax a λλ-+--+=,当=1λ,曲线方程为220ax a -+=,即2ax =,这是线段AB 的垂直平分线 当1λ≠时,可化为2222211a a x y λλλ⎛⎫⎛⎫-+= ⎪ ⎪--⎝⎭⎝⎭,这是圆的标准方程 可知当1λ≠时,曲线是圆.师:通过以上探究不难发现,当动点到两个定点的距离之比为定值且该定值不是1时,点的轨迹是圆,这样的圆在数学上叫做阿氏圆.显然圆心与两个定点共线,且两个定点一个在圆内,一个在圆外,明白了这些有助于我们画出图形辅助分析问题.同学们可否利用这个知识点来解决本道试题呢？生:由题目条件“2AB AC =”可知点如果将B ,C 两点固定,则点A 的轨迹是圆. 以B 为坐标原点,BC 所在直线为x 轴,建立平面直角坐标系,则()0,0B ,(),0C a ,设(),A x y ,由2AB AC =,得()22222x y x a y +=-+,化简得2224439a x a y ⎛⎫-+=⎪⎝⎭, 故点A 在以4,03a ⎛⎫⎪⎝⎭为圆心,半径为23a 的圆上运动,则23y a ≤.又ABC ∆的面积为1,所以112a y ⋅⋅=,即2y a =又223aa ≤,所以3a ≥,即BC 的最小值为3. 师：显然,上述解法与原解法相比,不仅计算量小很多,更是在思维上技高一筹,凸显了深刻的数学思维,大道至简.同学们能够意识到本题实际上是动态问题,将思维由静态转化为动态,有一种豁然开朗的感觉.【设计意图】在环节1当中,虽然学生解决了问题,但是思维局限在静态,无法从动态的角度理解本道试题.此时教师引导学生回顾课本的例题,重温阿氏圆的探究过程,启发学生从动态的角度分析本道试题,从而给出基于深度思维的解答,提高了学生的数学思维能力. 3.强化训练,提升思维师:请同学们完成练习1 练习1:2023年皖东名校联盟高三9月第二次数学质检 已知,,又点在圆上且满足（）,则生（众）：设()11,P x y ,()()()()22222211x y x y -+-=-+-整理得22222222242482111k k kx y x yk k k---++++=---,与比较系数得2240k-=,故2k=师:同学们基本掌握了求阿氏圆方程的方法,并顺利解决问题.大家再开动脑筋想想,如果不设点,不求圆的方程,可以解决问题吗？生：观察题目条件,不难发现,不需要求出圆的方程,只需找两个特殊的点,列出两个等量关系求解.图(1)师:找哪两个点比较合适呢？生:找直线AB与圆的两个交点解:如图(1)所示,,,,,,则 (1),,因为,即,代入(1)得.【设计意图】在环节2当中,学生已经较好地掌握了阿氏圆的求解,在此基础上,给出练习1,学生由于受到先前思维的影响,会想到用设点求出圆方程的方法解决问题.此时教师不失时机地引导学生思考,一定要求出圆的方程吗？可否有更简便的方法？学生通过观察图形,发现只需在图形中寻找到两个特殊点即可解决问题,从而拓展了自己的思维,进一步提升了解题能力,收获到成功的喜悦.练习2:清华大学中学生标准学术能力诊断性测试2023年9月测试数学第7题已知中,,角的平分线交于,若,则面积的最大值为师:本题中,题目没有给出动点A与两个定点B,C的距离之比,如何得到这个距离之比？生:可以借助内角平分线定理和条件得到.图(2)解:如图(2)所示,,,,故点的轨迹是圆,且圆过点.由于,所以,故.则,,所以,故.所以,即圆的半径为2,所以面积的最大值为.【设计意图】在本题中,题目条件并没有给出ABACλ=这样的条件,而是隐含在内角平分线当中.学生必须结合三角形的内角平分线定理挖掘出来才能顺利求解.这就训练了学生分析问题,解决问题的能力.练习3：已知为坐标原点,,在直线上,,动点满足,则的最小值为图(3)解:如图(3)所示,由已知点的轨迹是一个圆,设半径为,,,则,,,解得,,.点到直线的距离,的最小值为.【设计意图】本题巧妙地将阿氏圆与圆外定点到圆上动点距离最值问题结合起来,体现了知识的交汇,这也是高考命题的一个重要原则.学生通过动脑思考,动手尝试,真正感受到试题的本质,提高了自己的数学思维,促进了深度学习.4.拓展思维,提升素养师:通过刚才大家的共同探究,同学们对阿氏圆的应用有了较为深刻的认识.阿氏圆是平面解析几何一个重要内容,事实上,在立体几何中,也有相关的考查.练习4:深圳实验学校2023--2024学年高二数学第16题已知正方体的棱长为2,点是正方体表面上上一个动点,且,则点形成的轨迹的长度为图(4)解:如图(4)所示,若面,设,则,所以,故所以点在以为圆心,为半径的圆弧上,所以弧长为若面,设圆心为,则,,设半径为,则,,由得,所以.设圆与交于点,易知为正三角形,所以弧的长度为同理,当面时,所得弧长的长度为故点形成的轨迹的长度为【设计意图】将学生的思维从二维的平面提升至三维的立体,极大地拓展了学生的知识面,让学生的思维插上想象的翅膀,闪耀出智慧的火花.真正达到了素养的培育和能力的提升.三、教学启示通过一道阿氏圆试题,引导学生回归课本,以教材例题为载体提炼出方法,进而解决陌生问题,引领学生的思维从低阶向高阶发展.在高中的数学教学中,要善于以课本例题为载体,进行小切口的深挖掘,使得学生会一题即会一类,从而较好地培养学生的数学思维能力,避免陷入题海战术.这也是新教材新高考的必然要求.数学课堂的首要任务是培养学生的数学思维，避免学生陷入题海.高考考查的是学生的思维,而不是硬背.从教材中的例题出发,提炼出解题方法,之后应用于复杂陌生的情境当中,让学生学会知识的正迁移,从而提升思维,提高学生解决问题的能力,从而更好地适应新高考要求.。