当前位置：文档之家 › 几种重要随机变量的数学期望及方差

几种重要随机变量的数学期望及方差

  • 格式：ppt
  • 大小：262.00 KB
  • 文档页数：5

下载文档原格式

  / 5

合集下载

概率论与数理统计 --- 第四章{随机变量的数字特征} 第一节：数学期望

概率论与数理统计 --- 第四章{随机变量的数字特征} 第一节：数学期望
32 30 17 21 0 1 2 3 1.27 100 100 100 100
这个数能否作为 X的平均值呢？
若统计100天,
可以想象, 若另外统计100天, 车工小张不出废品, 这另外100天每天的平均废品数也不一定是1.27. 一般来说, 若统计n天 ,
(假定小张每天至多出三件废品)
又设飞机机翼受到的正压力W 是V 的函数 : W kV 2 ( k 0, 常数), 求W 的数学期望.
解: 由上面的公式
1 1 2 E (W ) kv f (v )dv kv dv ka a 3 0
2 2

a
例7 设二维连续型随机变量（X , Y）的概率密度为
A sin( x y ) 0 x , 0 y f ( x, y) 2 2 0 其它 (1)求系数A , ( 2)求E ( X ), E ( XY ).
x f ( x )x
i i i
i
阴影面积近似为
这正是:


f ( xi )xi

x f ( x )dx
的渐近和式.
小区间[xi, xi+1)
定义: 设X是连续型随机变量, 其密度函数为 f (x), 如果积分: xf ( x )dx
概率论


绝对收敛, 则称此积分值为X的数学期望, 即:
2. 设二维连续型随机变量 (X, Y) 的联合概率密度为 f (x, y), 则： E ( X )
E (Y )


xf X ( x )dx

yfY
( y )dy




xf ( x , y )dxdy,

常用分布的数学期望及方差

常用分布的数学期望及方差
( x − µ )2 2σ 2
−
t2 2
dt , (
x−µ
σ
= t)
=
σ
2π
∫ te
t2 − 2
dt +
∞
µ 2π
∫e
t2 − 2
dt = µ
−
DX = E ( X − µ ) =
2
=
σ2 =− te 2π
σ t 2π −∞
∞
∫
2 2
t2 − e 2
t2 − 2
−∞
∫ (x − µ)
σ
2 ∞
2
1 2π σ
且 X 1 ,L , X n 独立，令 X = X 1 + L + X n ，则 X 的可能 取值为 0,1,…n，
P{ X = k } = C nk p k q n − k , k = 0 , L , n
EX = ∑ EX i = np ， DX = ∑ DX i = npq,
i =1 i =1 n n
n
= n ( n − 1) p 2 ∑
n! n! = p ( k − 1) p k −1 q n − k + p p k −1 q n − k ( k − 1)! ( n − k )! ( k − 1)! ( n − k )! k =1 k =1
∑
∑
n
( n − 2)! p k − 2 q n − 2 − ( k − 2 ) + np k = 2 ( k − 2)!( n − 2 − ( k − 2))!
泊 分 3． 松 布
设 X 服从参数为λ泊松分布， 其分布律为 P{ X = k} =
EX =
λk
∑

概率论课程第四章

概率论课程第四章

第四章 数字特征前面我们介绍了随机变量及其分布，对于一个随机变量，只要知道了它的分布（分布函数或分布律、分布密度），它取值的概率规律就全部掌握了。

但在实际问题中，一个随机变量的分布往往不易得到，且常常只需知道随机变量的某几个特征就够了。

例如检查棉花的质量时，我们关心的是棉花纤维的平均长度和纤维长度与平均长度的偏差大小，这些数字反映了随机变量的一些特性，我们称能够反映随机变量特征的数字为随机变量的数字特征。

本章将介绍几个最常用的数字特征：数学期望、方差、协方差和相关系数。

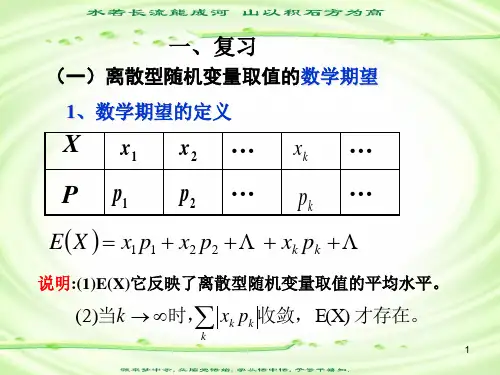
第一节 数学期望一、离散型随机变量的数学期望数学期望反映的是随机变量取值的集中位置的特征，能够满足这一要求的自然是随机变量的平均取值，那么这个平均取值如何得到呢？怎样定义，我们先看一个例题例1：全班40名同学，其年龄与人数统计如下：该班同学的平均年龄为：4092115201519118⨯+⨯+⨯+⨯=a8.194092140152040151940118=⨯+⨯+⨯+⨯=若令X 表示从该班同学中任选一同学的年龄，则X 的分布律为于是，X 取值的平均值，即该班同学年龄的平均值为4092140152040151940118)(⨯+⨯+⨯+⨯==a X E8.19==∑ii i p x定义1：设X 为离散型随机变量，其分布律为i i p x X P ==}{， ,2,1=i如果级数 绝对收敛，则此级数为X 的数学期望（或均值），记为 E(X)，即 ∑=ii i p x X E )(意义：E(X)表示X 取值的（加权）平均值。

如果级数 不绝对收敛，则称数学期望不存在。

例2：甲、乙射手进行射击比赛，设甲中的环数为X1，乙中的环数为X2，已知 X1和X2的分布律分别为：问谁的平均击中环数高？解：甲的平均击中环数为 E(X1)=8 0.3+9 0.1+10 0.6=9.3 乙的平均击中环数为 E(X2)=8 0.2+9 0.5+10 0.3=9.1 可见E(X1)> E(X2)，即甲的平均击中环数高于乙的平均击中环数。

随机变量的期望与方差

随机变量的期望与方差

5．(2017· 沧州七校联考)抛掷两枚骰子，当至少有一枚5点 或一枚6点出现时，就说这次实验成功，则在30次实验中成功次 数X的均值是( 55 A. 6 50 C. 3 ) 40 B. 3 D．10
答案 C 1 1 解析 至少有一枚5点或一枚6点的概率为1－(1－3)(1－3)＝ 4 5 5 5 50 1－9＝9.∴X～B(30，9)，∴E(X)＝30×9＝ 3 .
n＋1 1 (2)E(X)＝ (1＋2＋…＋n)＝ ， n 2 n＋1 2 n＋1 2 n＋1 2 1 D(X)＝n[(1－ 2 ) ＋(2－ 2 ) ＋…＋(n－ 2 ) ] n＋1 2 1 2 1 2 2 2 2 ＝ (1 ＋2 ＋3 ＋…＋n )－( ) ＝ (n －1)． n 2 12
(3)设X为该生选对试题个数，Y为成绩． 则X～B(50，0.7)，Y＝3X. ∴E(X)＝50×0.7＝35，D(X)＝50×0.7×0.3＝10.5. 故E(Y)＝E(3X)＝3E(X)＝105， D(Y)＝D(3X)＝9D(X)＝94.5. n＋1 1 2 35 【答案】 (1)3.5，10， (2) ， (n －1) 12 2 12 (3)105，94.5
)
9 D.20
答案 C 解析 由分布列的性质知2x＋3x＋7x＋2x＋3x＋x＝1，∴x 1 20 ＝ ，∴E(x)＝0· 2x＋1· 3x＋2· 7x＋3· 2x＋4· 3x＋5·x＝40x＝ . 18 9
2．设随机变量X～B(n，p)，且E(X)＝1，6，D(X)＝1.28， 则( ) A．n＝8，p＝0.2 C．n＝5，p＝0.32 B．n＝4，p＝0.4 D．n＝7，p＝0.45
第 课时 随机变量的期望与方差
…2017 考钢下载…
1．了解离散型随机变量的数学期望、方差、标准差的意 义，会根据离散型随机变量的分布列求它的期望、方差． 2．离散型随机变量的期望与方差在现实生活中有着重要意 义，因此求期望、方差是应用题的命题方向．

常用分布的数学期望及方差

常用分布的数学期望及方差

方差的性质
方差具有可加性
对于两个独立的随机变量X和Y，有Var(X+Y) = Var(X) + Var(Y)。
方差具有对称性
对于一个常数a和随机变量X，有Var(aX) = |a|^2 * Var(X)。
方差具有非负性
对于随机变量X，有Var(X) >= 0，其中 Var(X) = 0当且仅当X是一个常数。
05 数学期望与方差的应用
在统计学中的应用
描述性统计
数学期望和方差用于描述一组数据的中心趋势和 离散程度，帮助我们了解数据的基本特征。
参数估计
通过样本数据的数学期望和方差，可以对总体参 数进行估计，如均值和方差的无偏估计。
假设检验
在假设检验中，数学期望和方差用于构建检验统 计量，判断原假设是否成立。
常见分布的数学期望
均匀分布的数学期望为
$E(X) = frac{a+b}{2}$，其中a和b是均匀分布的下限和上 限。
柯西分布的数学期望为
$E(X) = frac{pi}{beta} sinh(frac{1}{beta})$，其中β是柯西 分布的参数。
拉普拉斯分布的数学期望为
$E(X) = frac{beta}{pi} tan(frac{pi}{beta})$，其中β是拉普 拉斯分布的参数。
03
泊松分布
正态分布是一种常见的连续型随机变量 分布，其方差记作σ²。正态分布的方差 描述了随机变量取值的分散程度。
二项分布是一种离散型随机变量分布， 用于描述在n次独立重复的伯努利试验 中成功的次数。其方差记作σ²，且σ² = np(1-p)，其中n是试验次数，p是单次 试验成功的概率。
泊松分布是一种离散型随机变量分布， 用于描述在一段时间内随机事件发生的 次数。其方差记作σ²，且σ² = λ，其中 λ是随机事件发生的平均速率。

六个常用分布的数学期望和方差

六个常用分布的数学期望和方差

即
12
若随机变量X~U( a , b ),则
ab
(b a)2
E(X)
, D( X )
2
12
五.指数分布
随机变量X服从参数为λ的指数分布，其概率密度为：
f
(
x)
1
θ
e
x θ
0
x0 x0
E(X )
xf ( x)dx
x
1
e
x θ
dx
x
（ x）de θ
0
θ
0
（
x）e
x
x
e dx
X X1 X2 Xn
E( X ) E( X1 ) E( X 2 ) E( X n ) np
D( X ) D( X1 ) D( X 2 ) D( X n ) np(1 p)
即： 若随机变量X~B( n , p ),则
E( X ) np，D( X ) np(1 p)
E[3( X 2 1)] 3E( X 2 ) 3
3{D( X ) [E( X )]2 } 3 33
例2.已知X和Y相互独立，且X在区间(1，5)上服从
均匀分布， Y ~ N (1,求9)(1, ) (X,Y)的联合概率密度;(2)
E(3X 4Y 2) , D(3X 4Y 2)
E( X ) xf ( x)dx
b
x
1
dx
a ba
1 x2 b
ba 2 a
ab 2
E( X 2 ) b x 2
1
b3 a3 dx
a 2 ab b2
a ba
3(b a)
3
D( X )
E( X 2 ) [E( X )]2

4.1随机变量的期望

4.1随机变量的期望
E ( X 1 ) 0 0 1 0.2 2 0.8 1.8(分） E ( X 2 ) 0 0.6 1 0.3 2 0.1 0.5(分）
例2 设X ~ ( ), 求E ( X ).
解 X的分布率为 P{ X k }
X的数学期望为 E( X ) k
E ( X ) = np
i 1 i
可见，服从参数为n和p的二项分布的随机变量X 的数学期望是 n p.
例9 把数字1,2,…,n任意地排成一列，如果数字k恰 好出现在第 k 个位置上，则称为一个巧合，求巧合 个数的数学期望. 解: 设巧合个数为X, 引入
1, 数字k恰好出现在第k个位置上 k=1,2, …,n Xk 否则 0， n 则 X Xk
1 3 6 6
1 2 6 6
1 3 P{ X 70} P ( AB ) P ( A) P ( B ) 6 6 其中A为事件"第一班车8 : 10到站" , B为事件"第二班车
9 : 30到站".候车时间X的数学期望为
3 2 1 3 2 E ( X ) 10 30 50 70 90 27.22分 6 6 36 36 36
因此，在对随机变量的研究中，确定某些数 字特征是重要的 .
在这些数字特征中，最常用的是
数学期望、方差、协方差和相关系数
一、离散型随机变量的数学期望
1.概念的引 入 例如：某7人的高数成绩为90，85，85，
80，80，75，60，则他们的平均成绩为
90 85 2 80 2 75 60 7 1 2 2 1 1 79.3 90 85 80 75 60 7 7 7 7 7

数学期望和方差

数学期望和方差
第四章
数学期望和方差
第四章 数学期望和方差
分布函数能够完整地描述随机变量的统计特 性，但在实际问题中，随机变量的分布函数较 难确定，而它的一些数字特征较易确定．并且 在很多实际问题中，只需知道随机变量的某些 数字特征也就够了.
另一方面，对于一些常用的重要分布，如二 项分布、泊松分布、指数分布、正态分布等， 只要知道了它们的某些数字特征，就能完全确 定其具体的分布.
8 8
9 10 11 12 7 15 10 10 50
则这 50 个零件的平均直径为
8 8 9 7 1015 1110 1210 50 10.14cm
第四章
数学期望和方差
换个角度看,从这50个零件中任取一个,它 的尺寸为随机变量X , 则X 的概率分布为 X P 8

x
| x| 但 | x | f ( x ) dx dx 发散. 2 (1 x )
它的数学期望不存在.
注：虽然f(x)是偶函数，但不能用定理1.1.
第四章
数学期望和方差
§4.2 数学期望的性质
设已知随机变量X的分布，我们需要计算的不 是X的数学期望， 而是X的某个函数的数学期望， 比如说g(X)的数学期望. 那么应该如何计算呢？ 更一般的，已知随机向量(X1 , X2 …,Xn ) 的联合分布， Y= g(X1, X2 …,Xn ) 是 (X1 , X2 …,Xn ) 的函数, 需要计算Y 的数学期 望，应该如何计算呢？ 我们下面就来处理这个 问题.
8 50
12
9
7 50
10
15 50
12
11
10 50
12
10 50
则这 50 个零件的平均直径为

第四章第3节多维随机变量的数学期望与协方差

第四章第3节多维随机变量的数学期望与协方差

Cov( X , X
i j i
j
)
n 1 1 n 2 2 2 n i j n ( n 1) n 1 n 1 2 2 n 2 n (n 1)
n 1 1 1 n n
4.3.4
定义4.3.2 称
相关系数
Corr(X, Y) =
为 X 与 Y 的相关系数.
课堂练习1
设 X ~ N(0, 1), Y ~ N(0, 1), Var(XY) = 0,
求 (X, Y) 的协差阵 .
1 1
1 1
课堂练习2
9 设 X, Y 的协差阵为 4
求相关阵 R.
4 , 16
1/ 3 1 R 1 1/ 3
第四章
随机变量的数字特征
§4.1 随机变量的数学期望与方差 §4.2 常见随机变量的期望与方差 §4.3 协方差、相关系数与矩
§4.3 协方差、相关系数与矩
4.3.1 定理 4.3.1 多维随机变量函数的数学期望 设 (X, Y) 是二维随机变量， Z = g(X, Y)，则
g ( xi , y j ) pij i j g ( x, y ) p ( x, y )dxdy
E(Z) = E[g(X, Y)] =
课堂练习
在长为 a 的线段上任取两点 X 与 Y，求两点间的平均长度. 求 E(|XY|)
4.3.2 数学期望与方差的运算性质
1. E(X+Y)=E(X)+E(Y) (性质3.4.1) 2. 当X与Y独立时，E(XY)=E(X) E(Y), (性质3.4.2)
讨论 X+Y 的方差
1. Var(XY) = Var(X)+ Var (Y) 2E[XE(X)][YE(Y)] 2. E[XE(X)][YE(Y)] = E(XY) E(X)E(Y) 3. 当X与Y独立时，E[XE(X)][YE(Y)] = 0. 4. 当X与Y独立时， Var(X Y) = Var(X)+ Var (Y) . 注意：以上命题反之不成立.

连续型随机变量的数学期望与方差

连续型随机变量的数学期望与方差

(1)D( )
E[
E( )]2
[x
E( )]2
p( x)dx
(2)方差的简便计算公式
D( )=E（ 2） E（2 ）
x2 p(x)dx
x p( x)dx
例2 随机变量的概率密度函数
6x(1 x)，当0 x 1
p(x)
0
当x 0或x 1时
求随机变量的方差。
12
4、方差的性质 设 k ,b,c均为常数，则有
E( ) xp(x)dx
15
2、数学期望的性质
(1)EaX b aEX b
(2)EaX aEX
(3)EX b EX b
(4)Eb b
(5)EX Y EX EY
(6)E( f ( )) f (x)p(x)dx
(6)E f ( ) f (xk )PK
k
16
（二）连续型随机变量ξ取值的方差
(1)D(c) 0
(2)D(k ) k 2D( ) (3)D( b) D( )
(4)D(k b) k 2D( )
13
下页
三、练习
• 课本第90页 第6题
14
四、小结 （一）连续型随机变量ξ取值的数学期望
1、连续型随机变量的数学期望的定义 p(x) 设连续型随机变量 的密度函数为
若积分 xp(x绝)d对x 收敛，则 的数学期望为：
x0 x1 x2 L xn
xi xi1 xi
b i
【xi
,
xi
）
+1
y p(x)
o
x0b0 x1 xi bi xi1
xn x
6
连续型随机变量ξ的概率分布
ξ 【x0 , x1）【x1, x2）

概率论 几种重要分布的方差

概率论 几种重要分布的方差
所以泊松分布方差为 D(X)=E(X2)-[E(X)]2=λ
泊松分布只含一个参数λ，因而只要知道它的数学 期望或方差就能完全确定它的分布，反之亦然。
四、均匀分布
设X在区间(a，b)上服从均匀分布，则 1 ,a x b ba f (x)
0, 其他
1 ab E ( x) x dx ba 2 a
D( X )

D( X ) E([ X E( X )]2 )
x

2
f ( x)dx
2
1 2
x e
x 2
2 2
dx
1 D( X ) 2
x e
2

x 2
2 2
D( X ) E ( X 2 ) [ E ( X )]2 1 (b a ) 2 ab 2 x dx a ba 12 2
b 2
b
即均匀分布方差为
(b a ) 2 12，其概率密度为
f (x)
则




2
2
D( X ) E ( X ) [ E ( X )]
2 2
2

2

1

2

1
2
即指数分布方差为
D ( x)
1
2
六、正态分布
若XN(µ,σ2)，其概率密度为 f ( x)
1 e 2

x 2
2 2
, x
E( X ) ,
三、泊松分布
设若 X(),其分布律为
k e P{ X k} k!
则 E( X )

常见分布函数的期望和方差

常见分布函数的期望和方差

常见分布函数的期望和方差
六种常见分布的期望和方差：
1、0-1分布
已知随机变量X，其中P{X=1} = p，P{X=0} = 1-p，其中0 < p < 1，则成X 服从参数为p的0-1分布。

其中期望为E（X）= p，方差D（X）= p（1-p）。

2、二项分布
n次独立的伯努利实验（伯努利实验是指每次实验有两种结果，每种结果概率恒定，比如抛硬币）。

其中期望E（X）= np，方差D（X）= np（1-p）。

3、泊松分布
其概率函数为P{X=k}=λ^k/(k!e^λ) k=0，1，2…...k代表的是变量的值。

其中期望和方差均为λ。

4、均匀分布
若连续型随机变量X具有概率密度，则称X在（a，b）上服从均匀分布。

其中期望E（X）= （a+b）/ 2 ，方差D（X）= （b-a）^2 / 12。

5、正态分布
若随机变量X服从一个数学期望为μ、方差为σ2的正态分布，记为N(μ，σ2)。

当μ= 0,σ= 1时的正态分布是标准正态分布。

其中期望是u，方差是σ的平方。

6、指数分布
若随机变量x服从参数为λ的指数分布，则记为X~E（λ）。

其中期望是E(X)=1/λ，方差是D(X)=1/λ。

随机变量的数字特征——期望,方差以及协方差

随机变量的数字特征——期望,方差以及协方差

例12: 设X ~ B(n , p), Y = eaX,求E（Y）。
解：
EY EeaX n eak P( X k)
k0
n
e
akC
k n
pk (1
p)nk
k0
n
C
k n
(e
a
p)k (1
p)nk
k0
(ea p (1 p))n
例13: 设X ~ U[0,], Y =sinX,求E（Y）。
g( xk )pk
k
绝对收敛，则Y 的数学期望存在，且
E(Y ) E[g( X )] g( xk ) pk
k
（2） 设X 为连续型随机变量, 其概率密度为 f (x)，且 Y= g(X)也是连续型随机变量。若
g( x) f ( x)dx
绝对收敛，则Y 的数学期望存在，且
E(Y ) E[g(X )] g(x) f (x)dx
2、几种常见离散型分布的数学期望
1） 两点分布 例3：设随机变量X服从参数为p 的两点分布，求EX
解： EX=0×(1-p)+1×p=p
2） 二项分布 例4：设随机变量X~B(n,p)，求EX 解： 易知 X 的概率分布为：
P( X k) Cnk pk (1 p)nk , k 0,1, , n
k!
E( X ) kP( X k)
k k e
k0
k0 k!
e
k 1
k0 (k 1)!
ee
例5 某人的一串钥匙上有n把钥匙，其中只有一把能 打开自己的家门，他随意地试用这串钥匙中的某一 把去开门. 若每把钥匙试开一次后除去，求打开门 时试开次数的数学期望.
解:设试开次数为X,

期望与方差

期望与方差

p X ( x), pY ( y) 为边际密度函数，则
E ( XY ) xyp( x, y )dxdy

由独立性
E ( XY ) xypX ( x) pY ( y )dxdy


xp X ( x)dx ypY ( y )dy E ( X ) E (Y )
（3）正态分布：设随机变 X ~ N ( , ) ,则
2
1 p X ( x) e 2
求其数学期望 EX。

( x )2 2 2
Hale Waihona Puke 1 解：按定义， EX x e dx ，作变换 2 x y , dx dy , 积分化为
( x )2 2 2
第三章
随机变量的数字特征
(Characteristic values of random variables)
尽管随机变量的概率分布全面地反映了其概率性质，但是， 在具体问题中，想求之经常是难以完成乃至无法做到。而有时 只需知道其中的参数就够了。例如，如果已知随机变量 X 服从
2
正态分布，只要知道其参数 、 为何，则便知其分布函数了。 本节主要讨论随机变量的两个数字特征，即数学期望(expected value or mean value)和方差(variance)的概率性质。
定义 1 设离散型随机变量 X 的分布律为
P{ X xk } pk , k 1,2,...
若级数 | xk | pk ，则称 X 的数学期望存在，并记为 E(X) 或 EX (MX)，其值定义为
EX xk pk
k
数学期望 EX 有时也称为期望或均值。 由定义，要计算 X 的数学期望，须首先知道其概率分布。 Ex:设 P{ X (1)

概率论与数理统计-CH3LX

概率论与数理统计-CH3LX

P{X m} C1m0 pm (1 p)10m
C1m0 0.4m 0.610m (m 0,1,2,10)
EX 2

10

m2C1m0
pm
(1

p)10m
m0
10
m2C1m0 0.4m 0.610m （比较繁）
m0
或由于 DX EX 2 ( EX )2 ，EX np 10 0.4 4
二．选择题
1．对于r v X 、Y ，若 EXY EX EY 则（ B）。
( A) D( XY) DX DY
(C ) X 与Y 独立
( B ) D( X Y) DX DY ( D) X 与Y 不独立
分析：因为由 EXY EX EY 知协方差为零。
2．设X 与Y 独立同分布，记U X Y ，其他EX 源自f (x, y)dxdyG
EX 2 x2 f (x, y)dxdy
G
201 xdx11x dy



2 3
201 x2dx11x dy
1 2
DX EX 2 (EX )2 1 同理 EY 2 ； DY 1 。
18
3
18
EXY 2xydxdy 012xdx11x ydy 5 /12

2 3
EX 2

01 2 x 3 dx

1 2
DX EX 2 (EX )2 1 18
同理可得 EY 2 ；DY 1 。
3
18
于是
EXY


G
2xydxdy
01 2 xdx11 x

(完整版)随机变量的数学期望与方差

(完整版)随机变量的数学期望与方差

第9讲 随机变量的数学期望与方差教学目的：1.掌握随机变量的数学期望及方差的定义。

2.熟练能计算随机变量的数学期望与方差。

教学重点：1．随机变量的数学期望2．随机变量函数的数学期望3．数学期望的性质4．方差的定义5．方差的性质教学难点：数学期望与方差的统计意义。

教学学时：2学时。

教学过程：第三章 随机变量的数字特征§3.1 数学期望在前面的课程中，我们讨论了随机变量及其分布，如果知道了随机变量X 的概率分布，那么X 的全部概率特征也就知道了。

然而，在实际问题中，概率分布一般是较难确定的，而在一些实际应用中，人们并不需要知道随机变量的一切概率性质，只要知道它的某些数字特征就够了。

因此，在对随机变量的研究中，确定其某些数字特征是重要的，而在这些数字特征中，最常用的是随机变量的数学期望和方差。

1．离散随机变量的数学期望我们来看一个问题：某车间对工人的生产情况进行考察。

车工小张每天生产的废品数X 是一个随机变量，如何定义X 取值的平均值呢？若统计100天，32天没有出废品，30天每天出一件废品，17天每天出两件废品，21天每天出三件废品。

这样可以得到这100天中每天的平均废品数为27.1100213100172100301100320=⨯+⨯+⨯+⨯ 这个数能作为X 取值的平均值吗？可以想象，若另外统计100天，车工小张不出废品，出一件、二件、三件废品的天数与前面的100天一般不会完全相同，这另外100天每天的平均废品数也不一定是1.27。

对于一个随机变量X ，若它全部可能取的值是Λ,,21x x ， 相应的概率为 Λ,,21P P ，则对X 作一系列观察(试验)所得X 的试验值的平均值是随机的。

但是，如果试验次数很大，出现k x 的频率会接近于K P ，于是试验值的平均值应接近∑∞=1k k k p x由此引入离散随机变量数学期望的定义。

定义1 设X 是离散随机变量，它的概率函数是Λ ,2 ,1,)()(====k P x X P x p K K k如果 ∑∞=1||k k k p x 收敛，定义X 的数学期望为∑∞==1)(k k k p x X E也就是说,离散随机变量的数学期望是一个绝对收敛的级数的和。

六个常用分布的数学期望和方差

六个常用分布的数学期望和方差

0
θ
0
（
x）e
x
x
e dx
0
0
x
e
θ
0
E( X 2 )
x 2 f ( x)dx
x2
1
x
eθ
dx
0
θ
x
（ x 2）de θ 0
（
x
2）e
x
x
2xe dx
0
0
（
ቤተ መጻሕፍቲ ባይዱ
2θx）de
x θ
0
（
2x）e
x
2
x
e dx
0
0
2
2
e
x
2θ 2， D( X ) E( X 2 ) [E( X )]2
X X1 X2 Xn
E( X ) E(X1 ) E(X 2 ) E(X n ) np
D( X ) D( X 1 ) D( X 2 ) D( X n ) np(1 p)
即： 若随机变量X~B( n , p ),则
E( X ) np，D( X ) np(1 p)
1
t2
( t )e 2 d t
t2
e 2 dt
2
2
D( X ) E{[ X E( X )]2 }
(x
)2
2
t2
t
2
e
2
dt
（令
t x ）
2
1
( x )2
e 2 2 dx
2
2
2
t2
( t )de
2
2 2
t2
te 2
t 2
e 2 dt
2
2
即

常见分布的数学期望与方差

常见分布的数学期望与方差

If X
P ( ), then
D(X )
二、常见的连续型随机变量的数学期望与方差
1.均匀分布的方差
分布密度
1 f (x) b a 0 a x b 其 它
E(X )
3 b a 2
1 2
(a b)
2
方差
E(X
2
)

b a
x
2
b a
2
dx
”；此后十年间，航空事业获得较快发展。
筹办航空事宜
处
三、从驿传到邮政 1．邮政
(1)初办邮政： 1896年成立“大清邮政局”，此后又设
邮传部 邮传正式脱离海关。
，
(2)进一步发展：1913年，北洋政府宣布裁撤全部驿站； 1920年，中国首次参加 万国邮联大会 。
2．电讯 (1)开端：1877年，福建巡抚在 办电报的开端。 (2)特点：进程曲折，发展缓慢，直到20世纪30年代情况才发生变 化。 3．交通通讯变化的影响
2

1

2
常见分布及其期望和方差列表
分布名称 数学期望E（X） 方差D（X）
p np
0-1分布
二项分布 泊松分布
pq
npq

a b 2

(b a ) 12
2
均匀分布
正态分布 指数分布

1

2
1


2
历史ⅱ岳麓版第13课交通与通讯 的变化资料
精品课件欢迎使用
[自读教材· 填要点] 一、铁路，更多的铁路 1．地位
铁路是
交通运输 建设的重点，便于国计民生，成为国民经济
发展的动脉。 2．出现 1881年，中国自建的第一条铁路——唐山 路建成通车。 1888年，宫廷专用铁路落成。 至胥各庄铁 开平

六个常用分布的数学期望和方差

六个常用分布的数学期望和方差
2
例1.已知 X ~ (3) , Y 2 X 1 , 求E (Y ) , D(Y ) , E[3( X 2 1)] 解：X ~ (3) , 则 E ( X ) 3 , D( X ) 3
E (Y ) E ( 2 X 1) 2 E ( X ) 1 5
D(Y ) D( 2 X 1) 4 D( X ) 12



xf ( x )dx

b
x
1 ba
dx
a

1 ba
x
2
b

ab 2
2 a
E( X )
2

b
x
2
1 ba
dx
b a
3
3
a
3(b a )
a ab b
2 2

a ab b
2
2
3
a 2ab b
2 2
D( X ) E ( X ) [ E ( X )]
即： 若随机变量X~B( n , p ),则
E ( X ) np，D( X ) np(1 p)
三.泊松分布
随机变量
P{ X k }
X ~ ( ) ，其分布律为：
λ e
k λ
,
k 0,1,2, ,
k!
E( X )
k
k 0

e
k

e

k!
(k 1)!

xf ( x )dx




x
1 2

e
dx （令 t
t
2
x

）
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

返回主目录
第四章 随机变量的数字特征
EX 2 k 2 k e k k e
k 0
k!
k 1 (k 1)!
§3 几种期望与方差
(k 1)
k
e
k e
k 1
(k 1)!
k 1 (k 1)!
2e
k 2 ee 2
k 2 (k 2)!
DX EX 2 (EX )2 2 2
DX EX 2 (EX )2 n2 p2 n p2 np n2 p2 np(1 p) npq
方法2：
第四章
随机变量的数字特征 §3 几种期望与方差
Xi 服从（0-1）分布， P{Xi 0} q, P{Xi 1} p,i 1,2, , n 且 X1, , X n 独立，令 X X1 X n ，则 X 的可能 取值为 0,1,…n，
第四章 随机变量的数字特征
n
n1 §3 几种期望与方差
EX np
C
k 1 n1
p
k
1
q
n1(k
1)
np
C
i n1
p
i
q
n1i
k 1
i0
np( p q)n1 np
EX 2
n
k 2 Cnk pk qnk
k 0
n
k2
n!
pkqnk
k 0
k!(n k )!
n
p
k
1
k
(k
n! 1)!(n
P{X k} Cnk pk qnk , k 0, , n
EX n EXi np ， DX n DX i npq,
i 1
i 1
设 X 服从参数为泊松分布，
其分布律为P{X k} k e ，k=0,1,...
k!
EX k k e e k1 e e
k 0 k!
k1 (k 1)!
P{| X | 3} P{ 3 X 3}
2(3) 1 0.9974
在上一节用切比晓夫不等式估计概率有：
P{| X | 3} 0.8889
返回主目录
k)! pk 1qnk
n
p (k 1)
n!
n
p k 1q nk p
n!
p k 1q nk
k 1
n(n 1)
p2
(k
n
1)!(n)!(n k )!
p q k 2 n2(k 2) np
k 2 (k 2)!(n 2 (k 2))!
n(n 1) p 2 ( p q) n2 np n 2 p 2 np 2 np
|
2 2
t2
e2
dt
2
返回主目录
第四章 随机变量的数字特征 §3 几种期望与方差
P{| X | } P{ X }
( ) ( ) (1) (1) 2(1) 1 0.6826
P{| X | 2} P{ 2 X 2 }
2(2) 1 0.9544
e 2 2 dx
2
1
(t
t2
)e 2
dt,
(
x
t)
2
t2
te 2 dt
t2
e 2 dt
2
2
DX E( X )2 (x )2
1
( x )2
e
2 2
dx, ( x t)
2
2t2
t2
e2
dt
2
t
2
e
t2 2
dt
2
t2
tde 2
2
2
2
2 2
t2
te 2
4.均匀分布
f
(x)
1/(b a), 0, 其它
a
x
b
。
b
EX xf (x)dx x 1 dx a b
ba
2
a
返回主目录
第四章 随机变量的数字特征
§3 几种期望与方差
b
DX EX 2 (EX)2 x2
1
dx ( a b)2 (b a)2
a ba
2
12
EX x
1
(x)2