2-杆系结构有限元分析报告

第2章杆系单元和杆系结构整体分析2.1杆系单元2.2杆系结构整体分析第2章杆系单元和杆系结构整体分析2.1杆系单元2.2杆系结构整体分析对象、任务对象任务对象：研究有限大小的个体(element)对象研究有限大小的个体任务：1. 建立应变与结点位移分量之间的关系;2. 建立应力与结点位移分量之间的关系;33. 建立结点力与结点位移分量之间的关系;4. 把作用在单元内的外载转化成结点荷载，即单元等效节点力。

一、分离单元1 结构离散取杆件与杆件交点、集中力作用点、杆件与支承的交点为节点。

相邻两节点间的杆件段是单元。

节点编号时力求单元两端点号差最小。

YX2 坐标系有限元中的标系有体标系和局部标系有限元中的坐标系有整体坐标系和局部坐标系。

对于一个结构，整体坐标系一般只有一个；而局部坐标系有很多个，一个单元就有一个局部坐标。

并标系有很多个个单元就有个局部标并且局部坐标系每一个单元的规定都是相同的，这样，同类型单元刚度矩阵相同。

YX杆系结构单元主要有铰接杆单元和梁单元两种类型。

它们都只有2个节点i 、j 。

¾约定：单元坐标系的原点置于节点i ；节点i 到j 的杆轴（形心轴）方向为单元坐标系中x 轴的正向。

y 轴、z 轴都与x 轴垂直，并符合右手螺旋法则。

¾对于梁单元，y 轴和z 轴分别为横截面上的两个惯性主轴惯性主轴。

·x yj·z i土木工程学院有限单元法二、杆单元单元分析维杆单元下图示出了一维铰接杆单元，横截面积为A ，长1、一维杆单元度为l ，弹性模量为E ，轴向分布载荷为p x 。

单元有2，单元坐标为一维坐标轴个结点i ，j ，单元坐标为维坐标轴x 。

··i j x p x u ju i l LINK土木工程学院有限单元法P-8··i x p x j l u ju i LINK⎫⎧=i e u ⎧单元结点位移向量{}⎭⎬⎩⎨j u δ单元结点力向量：⎬⎫⎨=j i e F F F }{⎭⎩（1）位移模式和形函数①位移模式因为只有2个结点，每个结点位移只有1个自由度，因此单元的位移模式可设为：12u a a x =+（3）式中a 1、a 2为待定常数，可由结点位移条件时x =x i 时，u =u ix =x j 时，u =u j确定。

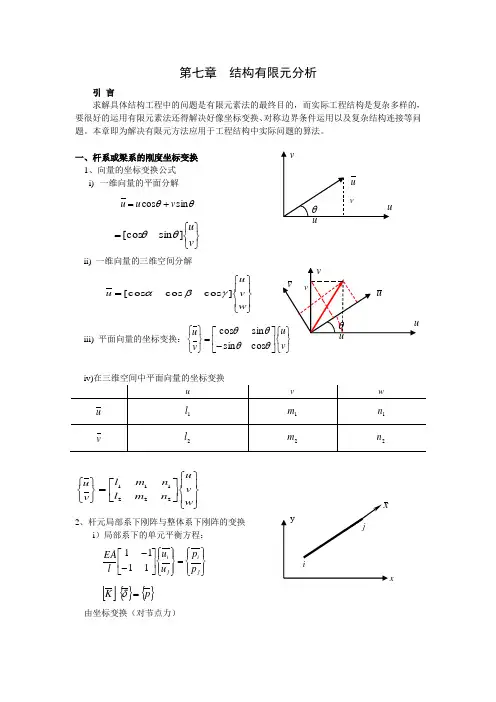
第七章 结构有限元分析引 言求解具体结构工程中的问题是有限元素法的最终目的，而实际工程结构是复杂多样的，要很好的运用有限元素法还得解决好像坐标变换、对称边界条件运用以及复杂结构连接等问题。

本章即为解决有限元方法应用于工程结构中实际问题的算法。

一、杆系或梁系的刚度坐标变换1、向量的坐标变换公式i) 一维向量的平面分解θθsin cos v u u +=⎭⎬⎫⎩⎨⎧=v u ]sin [cos θθii) 一维向量的三维空间分解⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧=w v u u ]cos cos [cos γβαiii) 平面向量的坐标变换：⎭⎩⎥⎦⎤⎢⎣⎡-=⎭⎬⎫⎩⎨⎧v v u θθθθcos sin sin cos⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎦⎤⎢⎣⎡=⎭⎬⎫⎩⎨⎧w v u n m l n m l v u 2221112、杆元局部系下刚阵与整体系下刚阵的变换 i ）局部系下的单元平衡方程：⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎦⎤⎢⎣⎡--j i j i p p u u l EA 1111 []{}{}p K =δ由坐标变换（对节点力）xx⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧j i jy jx iy ix p p p p p p θθθθsin 0cos 00sin 0cos =>{}{}P P T T ⎥⎦⎤⎢⎣⎡=λλ00 由局部坐标系下的平衡方程{}[]{}δλλK P T T⎥⎦⎤⎢⎣⎡=00 由位移（节点）的坐标变换[]⎭⎬⎫⎩⎨⎧=i i i v u u θθs i n c o sc o s s i n0000c o ss i n i i i j j j u u v u u v θθθθ⎧⎫⎪⎪⎧⎫⎡⎤⎪⎪⎪⎪=⎨⎬⎨⎬⎢⎥⎣⎦⎪⎪⎪⎪⎩⎭⎪⎪⎩⎭{}{}δλλδ⎥⎦⎤⎢⎣⎡=00 代入{P }的表达式：{}[]{}δλλλλ⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡=0000K P T T{}}]{][[]'[δT K T P =故 []]][[]'[T K T K = 杆系举例：○1节点编号 ○2单元编号 ○3形成各单元的总体坐标系下刚阵 ○4单元拼装 ○5求解总体刚度方程3、平面梁元局部系下刚阵到整体系的坐标变换 i). 梁元局部系下的单元刚度平衡方程⑧⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡--------j j y j x i i y i x j jj i i i l EIl EI lEI l EIl EI l EI l EI lEIlEAlEAlEI l EI lEI l EI l EI l EI l EIl EIlEA lEA M P P M P P v u v u θθ46266126122646612612222323222323000000000000000⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎦⎤⎢⎣⎡j i j i P P K K K K δδ22211211ii) 坐标变换⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧i i i i i i v u y y x y y x x x v u θθ1000),cos(),cos(0),cos(),cos(⎭⎬⎫⎩⎨⎧⎥⎦⎤⎢⎣⎡=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧j i j i δδλλδδ00[][]⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡=22211211222112110000K K K K K K K K K K TT T T Tλλλλλλλλλλλλ iii) 空间梁元有更复杂的变换关系iv ）其它单元的坐标变换Homework : 列出平面弹性问题的刚度矩阵向三维空间的变换i) 实际问题ii ）问题：一些节点在总体坐标系下，一些节点是在局部坐标系下，这类问题称为混合坐标架问题，即最终的刚度矩阵是一个混合标架下的形式。

有限元分析实验报告有限元分析实验报告一、实验基本要求根据实验指导书的要求能够独立的使用ANSYS 软件操作并在计算机上运行，学会判断结果及结构的分析，学会建立机械优化设计的数学模型，合理选用优化方法，独立的解决机械优化设计的实际问题。

二、实验目的1. 加深对机械优化设计方法的理解2. 掌握几种常用的最优化设计方法3. 能够熟练使用ANSYS 软件操作，培养学生解决案例的能力4. 培养学生灵活运用优化设计方法解决机械工程中的具体实例三、实验软件及设备计算机一台、一种应用软件如ANSYS四、实验内容实验报告例题实训1——衍架的结构静力分析图2-2所示为由9个杆件组成的衍架结构，两端分别在1，4点用铰链支承，3点受到一个方向向下的力F y , 衍架的尺寸已在图中标出，单位： m。

试计算各杆件的受力。

其他已知参数如下: 弹性模量（也称扬式模量）E=206GPa；泊松比μ=0.3；作用力F y =-1000N；杆件的2横截面积A=0.125m.一、 ANSYS8.0的启动与设置图2-2 衍架结构简图1．启动。

点击：开始>所有程序> ANSYS8.0> ANSYS ，即可进入ANSYS 图形用户主界面。

图2-4 Preference 参数设置对话框2．功能设置。

电击主菜单中的“Preference ”菜单，弹出“参数设置”对话框，选中“Structural ”复选框，点击“OK ”按钮，关闭对话框，如图2-4所示。

本步骤的目的是为了仅使用该软件的结构分析功能，以简化主菜单中各级子菜单的结构。

3．系统单位设置。

由于ANSYS 软件系统默认的单位为英制，因此，在分析之前，应将其设置成国际公制单位。

在命令输入栏中键入“/UNITS，SI ”，然后回车即可。

（注：SI 表示国际公制单位）二单元类型，几何特性及材料特性定义1．定义单元类型。

2．定义几何特性。

3．定义材料特性。

三衍架分析模型的建立1．生成节点。

杆系结构的有限元法分析有限元法是一种结构分析方法，常用于分析各种不同类型的结构系统，其中包括杆系结构。

杆系结构是由杆件连接而成的桁架结构，常见于桥梁、塔架和支撑结构等。

利用有限元法进行杆系结构的分析，可以得到结构的位移、应力、应变和刚度等信息，帮助工程师评估结构的稳定性和安全性。

下面将介绍杆系结构的有限元法分析的步骤。

首先，进行前期准备工作。

这包括收集与结构相关的几何信息（如杆件长度、截面形状等）、边界条件（如固定支座、外载荷等）和材料性质（如材料的弹性模量、密度等）。

这些信息将是有限元模型建立所需要的输入参数。

接下来，建立有限元模型。

将杆系结构离散化为一个个的杆单元，采用有限元方法对每个杆单元进行离散近似。

常用的杆单元包括横截面线性杆单元、三节点弯曲杆单元和非线性杆单元等。

然后，确定单元刚度矩阵。

对于横截面线性杆单元，其刚度矩阵可以根据材料性质和几何信息计算得到。

对于弯曲杆单元和非线性杆单元，则需要考虑附加的几何和材料非线性效应。

接着，组装全局刚度矩阵。

将所有杆单元的刚度矩阵按照其关联的节点自由度进行组装。

在组装过程中，需要考虑杆单元之间的关联关系，确保刚度矩阵的正确性和完整性。

然后，应用边界条件。

根据实际情况，将已知的边界条件（如固定支座、已知位移等）施加到全局刚度矩阵中。

这将改变全局刚度矩阵的特征值和特征向量，从而影响结构的响应。

接下来，求解结构的位移和应力。

通过求解结构的整体刚度方程以及施加的边界条件，可以得到结构的位移解向量和应力解向量。

位移解向量描述了结构的变形情况，而应力解向量体现了结构的应力分布情况。

最后，进行后处理。

在得到位移和应力解后，可以计算结构的应变分布、变形形态以及额外的设计指标。

通过这些结果，可以对结构的性能进行评估，以便优化设计。

综上所述，杆系结构的有限元法分析包括前期准备、建立有限元模型、确定单元刚度矩阵、组装全局刚度矩阵、应用边界条件、求解结构的位移和应力以及后处理等步骤。

2杆系结构的有限元有限元法是一种常用的数值计算方法，用于求解连续介质力学问题。

它将连续结构简化为有限个节点和单元，通过在这些节点上建立适当的位移函数，进而得到结构的应力、应变和位移分布。

有限元法的应用非常广泛，特别是在结构力学领域。

本文将重点介绍2杆系结构的有限元方法。

2杆系结构是指由两个杆件组成的简单结构，它们一端固定，另一端可以自由位移。

2杆系结构的分析问题可以用一维线弹性力学理论来描述。

首先，我们需要对2杆系结构进行离散化，将其简化为有限个节点和单元。

节点是结构的关键点，单元是相邻节点之间的连接。

我们可以选择线性单元，即每个单元内部的位移是线性分布的，也可以选择非线性单元，进行更为精确的计算。

然后，在每个节点上引入适当的位移函数，用来描述结构的变形情况。

接下来，我们需要确定2杆系结构的刚度矩阵和荷载向量。

刚度矩阵描述了杆件的刚度关系，荷载向量描述了外部施加的荷载。

通过求解结构的平衡方程，我们可以得到结构的位移。

这个过程可以通过线性代数方法来实现，也可以使用迭代方法求解非线性方程组。

最后，我们可以通过计算得到的位移来计算结构的应力和应变分布。

这些信息可以用来评估结构的稳定性和耐久性。

此外，我们还可以通过有限元法来模拟结构在不同工况下的响应，进一步优化设计。

总结来说，2杆系结构的有限元方法是一种有效的工具，用于分析和设计各种类型的结构。

它可以提供结构的应力、应变和位移分布，帮助工程师评估结构的性能和安全性。

这种方法的应用范围非常广泛，可以用于建筑、桥梁、机械等领域。

在实际工程中，我们可以使用专业的有限元软件，例如ANSYS、ABAQUS等，来进行2杆系结构的有限元分析。