杆件结构的有限元法

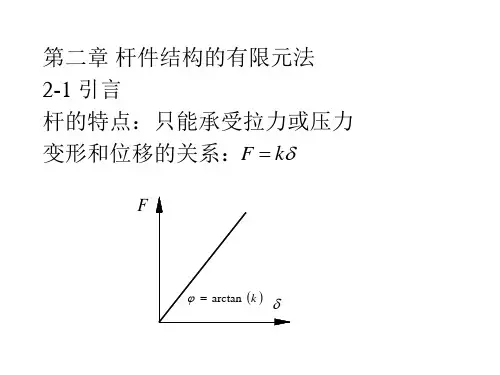
第六章杆件系统结构有限元法杆件系统是由几何特征为长度比横梁面的两个尺寸大很多的杆件连接而成的结构体系。

起重机械和运输机械的动臂、汽车的车架、钢结构等，都是由金属的杆件组成的。

杆件系统的有限元法在机械、建筑、航空、造船等各个工程领域得到了广泛的应用。

若杆件之间由铰相连，并且外载荷都作用在铰节点上，则该体系称为桁架。

有限元中将桁架的单元称为杆单元，即桁架是由仅承受轴向拉压的杆单元的集合。

如果杆件之间是由刚性连接，则该体系是刚架，刚架的单元称为梁单元。

梁单元可以承受轴力、弯矩、剪力及扭矩的作用。

第一节等截面梁单元平面刚架结构——所有杆件的轴线以及所有外力作用线都位于同一平面内，并且各杆件都能在此平面内产生平面弯曲，从而结构的各个节点位移都将发生在这个平面内。

一、结构离散化原则：杆件的交叉点、边界点、集中力作用点、位移约束点、分布力突变的位置都要布置成节点，而不同横截面的分界面和不同材料的分界面都要成为单元的分界面。

平面桁架对于桁架结构，因每个杆件都是一个二力杆，故每个杆件可设置成一个单元。

平面桁架结构每个节点有2个自由度，分别是u 和v ，每个单元有4个自由度。

最大半带宽B=(2+1)×2=6。

一维单元和二维单元的混合应用：左边部分是平面问题的二维板件结构（黑线部分），右面框架部分是一维杆件结构（红线部分）。

xy采用平面4节点四边形单元模拟二维板件，用平面杆单元单元模拟一维杆件结构。

离散化后，共有37个节点，32个单元，其中4节点四边形单元16个，杆单元单元16个。

因为平面4节点四边形单元和平面杆单元单元每个节点都有2个自由度，4节点四边形单元的刚度矩阵是8×8，平面杆单元的刚度矩阵是4×4。

整体刚度矩阵刚[]k 的维数是227474n n ⨯=⨯。

其中部分总刚子块为[](1)(2)(3)(4)777777777722k k k k k ⨯⎡⎤⎡⎤⎡⎤⎡⎤=+++⎣⎦⎣⎦⎣⎦⎣⎦(4)(6)(19)11,1111,1111,1111,1122k k k k ⨯⎡⎤⎡⎤⎡⎤⎡⎤=++⎣⎦⎣⎦⎣⎦⎣⎦最大半带宽B=［(8-2) +1］×2=14。

第9章 矩阵位移法9.1 复习笔记一、矩阵位移法的基本思路矩阵位移法又称为杆件结构的有限元法。

分析的两个基本步骤：（1）单元分析；（2）整体分析。

单元分析：建立杆端力与杆端位移间的刚度方程，形成单元刚度矩阵。

整体分析：将单元合成整体，按照刚度集成规则形成整体刚度矩阵，建立位移基本方程。

二、单元刚度矩阵（局部坐标系）进行单元分析，推导单元刚度方程和单元刚度矩阵。

单元刚度方程是指由单元杆端位移求单元杆端力的一组方程，可以用“”表示，由位移求力称为“正问题”。

相应的由力求位移称为“反问题”。

正问题的解是唯一的确定的，但是反问题则可能无解，如果有解也非唯一解。

当外部荷载为不平衡力系时，反问题无解；当外荷载为平衡力系时，反问题有解但是因为杆件除本身变形外还可有任意刚体位移，此时反问题的解不唯一。

本书暂不考虑反问题的求解。

1．一般单元图9-1所示为平面刚架中的一个等截面直杆单元.单元的两个端点采用局部编码1和2，由端点1到端点2的方向规定为杆轴的正方向，在图中用箭头标明。

F →∆e图9-1图中采用坐标系，其中轴与杆轴重合。

这坐标系称为单元坐标系或者局部坐标系。

字母、的上面都画了一横，作为局部坐标系的标志。

推导单元刚度方程时，有以下几点需要注意：重新规定正负号规则、讨论杆件单元的一般情况、采用矩阵表示形式。

在局部坐标系中，图9-2所示的位移、力分量方向为正方向。

图9-2杆件性质：长度l ，截面面积A ，截面惯性矩I ，弹性模量E ；杆端位移u 、v 、θ。

根据杆端位移可以推导出下面两组刚度方程：（9-1）x y x x y（9-2）将上述六个刚度方程列成矩阵形式：（9-3）其中就是局部坐标系下单元刚度矩阵，即为（9-4）2．单元刚度矩阵的性质 （1）单元刚度系数的意义e e ek F∆=eK代表单元杆端第j 个位移分量等于1时所引起的第i 个杆端力分量。

（2）是对称矩阵，即。

（3）一般单元的是奇异矩阵，即，因此不存在逆矩阵。

第五章 杆系结构的有限元法 5.1 引言杆系结构是工程中应用较为广泛的结构体系，包括平面或空间形式的梁、桁架、刚架、拱等。

其组成形式虽然复杂多样，但用计算机进行分析时却较为简单。

杆系结构中的每个杆件都是一个明显的单元。

杆件的两个端点自然形成有限元法的节点，杆件与杆件之间则用节点相连接。

显然，只要建立起杆件两端位移与杆端力之间的关系，则整体平衡方程的建立与前几章完全相同。

杆端位移与杆端力之间的关系，可用多种方法建立，包括前面几章一直采用的虚功原理，但是采用材料力学、结构力学的某些结论，不仅物理概念清晰、直观，而且推导过程简单明了。

因此，本章将采用这种方法进行单元分析。

至于整体平衡方程的建立，则和前面几章所讲的方法一样，即借助于单位定位向量，利用单元集成法进行。

5.2 平面桁架的有限元分析平面桁架在计算上有以下几个特点： 1． 杆件的每个节点仅有两个线位移； 2． 杆件之间的连接为理想铰，即在节点处各杆件可相对自由转动，且杆件轴线交于一点。

3． 外载荷均为作用于节点的集中力。

由于以上特点，所以在理论上各杆件只产生轴向拉、压力，截面应力分布均匀，材料可得到充分利用，因此桁架结构往往用于大跨结构。

5.2.1 局部坐标系下的单元刚度矩阵从平面桁架中任取一根杆件作为单元，称作桁架单元，单元长为L ，横截面面积为A ，图5.1。

两端节点分别用i 和j 表示，规定从i 到j 的连线方向为局部坐标x 轴，垂直于x 的方向为y 轴。

图5.1由于桁架中各杆只产生轴向力和轴向变形，所以节点i 和j 只发生沿x 方向的位移，用i u 和j u 表示，相应的杆端轴力分别用xi F 和xj F 表示。

由虎克定律可推得)()()(j i i j xj j i xi u u L EA u u L EA F u u LEAF --=-=-=将这两个式子写成矩阵形式，就是e j i exj xi u u L EA LEA L EA L EA F F ⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧ (5.1)显然，在局部坐标系下，i 、j 两节点沿y 轴方向的位移0==j i v v ，在y 轴方向的节点力0==yj yi F F 。

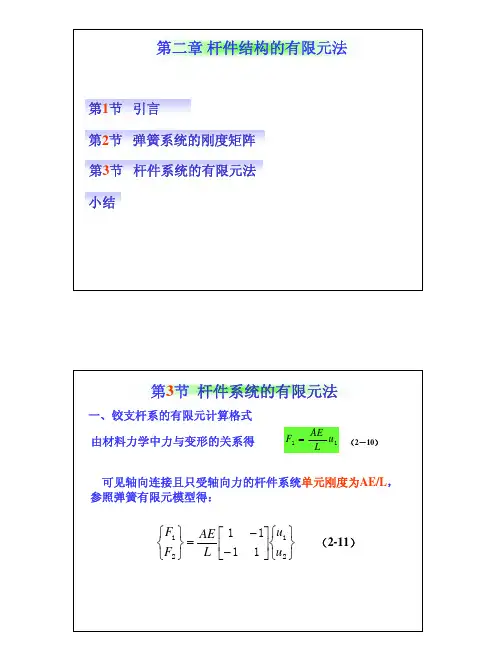
杆系结构的有限元法分析有限元法是一种结构分析方法，常用于分析各种不同类型的结构系统，其中包括杆系结构。

杆系结构是由杆件连接而成的桁架结构，常见于桥梁、塔架和支撑结构等。

利用有限元法进行杆系结构的分析，可以得到结构的位移、应力、应变和刚度等信息，帮助工程师评估结构的稳定性和安全性。

下面将介绍杆系结构的有限元法分析的步骤。

首先，进行前期准备工作。

这包括收集与结构相关的几何信息（如杆件长度、截面形状等）、边界条件（如固定支座、外载荷等）和材料性质（如材料的弹性模量、密度等）。

这些信息将是有限元模型建立所需要的输入参数。

接下来，建立有限元模型。

将杆系结构离散化为一个个的杆单元，采用有限元方法对每个杆单元进行离散近似。

常用的杆单元包括横截面线性杆单元、三节点弯曲杆单元和非线性杆单元等。

然后，确定单元刚度矩阵。

对于横截面线性杆单元，其刚度矩阵可以根据材料性质和几何信息计算得到。

对于弯曲杆单元和非线性杆单元，则需要考虑附加的几何和材料非线性效应。

接着，组装全局刚度矩阵。

将所有杆单元的刚度矩阵按照其关联的节点自由度进行组装。

在组装过程中，需要考虑杆单元之间的关联关系，确保刚度矩阵的正确性和完整性。

然后，应用边界条件。

根据实际情况，将已知的边界条件（如固定支座、已知位移等）施加到全局刚度矩阵中。

这将改变全局刚度矩阵的特征值和特征向量，从而影响结构的响应。

接下来，求解结构的位移和应力。

通过求解结构的整体刚度方程以及施加的边界条件，可以得到结构的位移解向量和应力解向量。

位移解向量描述了结构的变形情况，而应力解向量体现了结构的应力分布情况。

最后，进行后处理。

在得到位移和应力解后，可以计算结构的应变分布、变形形态以及额外的设计指标。

通过这些结果，可以对结构的性能进行评估，以便优化设计。

综上所述，杆系结构的有限元法分析包括前期准备、建立有限元模型、确定单元刚度矩阵、组装全局刚度矩阵、应用边界条件、求解结构的位移和应力以及后处理等步骤。