大学概率论之条件概率乘法公式
- 格式：ppt
- 大小：279.50 KB
- 文档页数：20
下载文档原格式
合集下载
条件概率乘法公式
P ( AB) P ( B) 0.4 P ( B | A) 0.5 P ( A) P ( A) 0.8
条件概率P(A|B)与P(A)的区别
每一个随机试验都是在一定条件下进行 的，设A是随机试验的一个事件，则P(A)是在 该试验条件下事件A发生的可能性大小.
而条件概率P(A|B)是在原条件下又添加 “B发生”这个条件时A发生的可能性大小， 即P(A|B)仍是概率.
设B={零件是乙厂生产}
300个 300个
乙厂生产
A={是标准件} 所求为P(AB).
乙厂生产
189个是
标准件
甲、乙共生产
1000 个
设B={零件是乙厂生产} 300个
A={是标准件} 所求为P(AB) .
乙厂生产
189个是
标准件
甲、乙共生产
若改为“发现它是乙厂生产的, 问它是标准件的概率是多少?”
监狱看守通知三个囚犯, 在他们中要随机 地选出一个处决 , 而把另外两个释放. 囚犯 甲请求看守秘密地告诉他,另外两个囚犯中谁 将获得自由.
丙 乙 甲
因为我已经知道他们两人中 至少有一人要获得自由，所 以你泄露这点消息是无妨的.
NO！
如果你知道了你的同伙中谁将获释， 那么，你自己被处决的概率就由 1/3增加到1/2,因为你就成了剩下的 两个囚犯中的一个了.
(5) 可列可加性 :设 B1 , B2 , 是两两不相容的事 件,则有
P Bi A P ( Bi A). i 1 i 1
4. 条件概率的计算 1) 用定义计算: P ( AB) P ( A | B) , P(B)>0 P ( B) 掷骰子 2)从加入条件后改变了的情况去算
P(A)与P(A |B)的区别在于两者发生的条件不同, 它们是两个不同的概念,在数值上一般也不同.
条件概率P(A|B)与P(A)的区别
每一个随机试验都是在一定条件下进行 的，设A是随机试验的一个事件，则P(A)是在 该试验条件下事件A发生的可能性大小.
而条件概率P(A|B)是在原条件下又添加 “B发生”这个条件时A发生的可能性大小， 即P(A|B)仍是概率.
设B={零件是乙厂生产}
300个 300个
乙厂生产
A={是标准件} 所求为P(AB).
乙厂生产
189个是
标准件
甲、乙共生产
1000 个
设B={零件是乙厂生产} 300个
A={是标准件} 所求为P(AB) .
乙厂生产
189个是
标准件
甲、乙共生产
若改为“发现它是乙厂生产的, 问它是标准件的概率是多少?”
监狱看守通知三个囚犯, 在他们中要随机 地选出一个处决 , 而把另外两个释放. 囚犯 甲请求看守秘密地告诉他,另外两个囚犯中谁 将获得自由.
丙 乙 甲
因为我已经知道他们两人中 至少有一人要获得自由，所 以你泄露这点消息是无妨的.
NO！
如果你知道了你的同伙中谁将获释， 那么，你自己被处决的概率就由 1/3增加到1/2,因为你就成了剩下的 两个囚犯中的一个了.
(5) 可列可加性 :设 B1 , B2 , 是两两不相容的事 件,则有
P Bi A P ( Bi A). i 1 i 1
4. 条件概率的计算 1) 用定义计算: P ( AB) P ( A | B) , P(B)>0 P ( B) 掷骰子 2)从加入条件后改变了的情况去算
P(A)与P(A |B)的区别在于两者发生的条件不同, 它们是两个不同的概念,在数值上一般也不同.
条件概率和乘法公式
机器学习算法
朴素贝叶斯分类器
01
朴素贝叶斯分类器是一种基于贝叶斯定理的分类算法，它利用
条件概率和乘法公式来计算给定特征下类别的概率。
隐马尔可夫模型
02
隐马尔可夫模型是一种用于序列标注和预测的模型，它利用条
件概率和乘法公式来计算状态转移和观测的概率。
条件随机场
03
条件随机场是一种用于自然语言处理的模型，它利用条件概率
03
在学习和应用概率论的过程中，我们需要注重培养自己的逻辑思维和分析能力 。通过深入思考和探究概率论中的问题，我们可以提高自己的数学素养和解决 问题的能力，为未来的学习和工作打下坚实的基础。
THANKS
感谢观看
• 在学习条件概率和乘法公式的过程中，我们需要掌握相关的概念和公式，并能 够灵活运用它们解决实际问题。同时，我们还需要了解条件概率和乘法公式的 局限性和假设条件，以避免在实际应用中出现错误。
• 除了条件概率和乘法公式，概率论中还有许多其他重要的概念和公式，例如全 概率公式、贝叶斯公式、独立性等。这些概念和公式之间有着密切的联系和相 互影响，我们需要系统地学习和理解它们，以建立完整的概率论知识体系。
02
乘法公式及其应用
乘法公式的推导
01
定义
乘法公式描述了两个事件A和B同时发生的概率与事件A发生的概率和事
件B发生的概率之间的关系。
02 03
推导
乘法公式基于概率的独立性假设，即事件A的发生不影响事件B的发生， 反之亦然。因此，事件A和事件B同时发生的概率等于各自发生的概率 的乘积。
公式
$P(A cap B) = P(A) times P(B)$
展望Βιβλιοθήκη 01随着科技的不断发展，概率论在各个领域的应用越来越广泛。未来，条件概率 和乘法公式等概率论知识将更加受到重视和应用。
14条件概率和乘法公式
球的取法为 P31P41, 其中, 第二次取得白球的取法
有 P31P21 种, 所以
P(B | A)
P31 P21 P31 P41
1 2
.
例 2 袋中有 5 个球, 其中 3 个红球 2 个白球, 现
从袋中不放回地连取两个, 已知第一次取得红球 时, 求第二次取得白球的概率.
解法 1 也可以直接用公式 (1) 计算, 因为第一次取走了一 个红球, 袋中只剩下 4 个球, 其中有两个白球, 再 从中任取一个, 取得白球的概率为 2/4, 所以
解 设 A {能活20年以上}, B {能活25年以上}
所求为P(B | A). 依题意,有
P( A)
P( AB) P( A)
P(B) P( A)
0.4 0.8
0.5.
三. 乘法公式 乘法公式：
P( AB) P( A)P(B A) (P( A) 0) P(B)P( A B) (P(B) 0)
解 记 Ai 为事件“第i 次取到的是黑球”(i 1,2). (1) 在已知 A1 发生, 即第一次取到的是黑球的条件 下, 第二次取球就在剩下的 2 个黑球、7 个白球共 9 个球中任取一个, 根据古典概率计算, 即有
P( A2 | A1) 2 / 9.
解 (2) 在已知 A2 发生, 即第二次取到的是黑球的
一. 条件概率的定义 设Ａ，Ｂ为同一个随机试验中的两个随机事件 ,
且Ｐ（A）＞０， 则
P(B | A) P( AB) P( A)
为在事件A发生的条件下，事件B发生的条件概率． 相应地，p(B)称为无条件概率．
条件概率 P(A|B)的样本空间
BA
BA
Sample space
P( AB)
概率论与数理统计公式总结(湖南大学)
(3) = ~t(n-1)
2.设 的 和 两个样本，则有：
(1)
5.相关性
对于随机变量X,Y下列结论是等价的：
(1)X与Y不相关 (3)ρ=0 (5)D(X Y)=D(X)+D(Y)
(2)Cov(X,Y)=0 (4)E(XY)=E(X)E(Y)
X,Y相互独立可以推出上述五个结论。
※切比雪夫不等式
表明：对于任意正数ε，当随机变量X的方差越小时，事件 的概率越小，其对立面概率越大。
则
定理(2)X Y相互独立，g(x)和h(y)是两个一元连续函数，则g(X)和h(Y)也相互独立。
定理(3) 则 。且 只差一个常数因子。
(重点)※期望与方差的性质
1期望的性质
(1)一维的：
若Y=g(X),
二维的：
若Z=g(X,Y),
(2)性质：E(C)=C E(CX)=CE(X) (C为常数)
E(X+Y)=E(X)+E(Y)
3.边缘概率密度函数
4.二维正态分布(还是看一下会比较好)
(1)二维正态分布中X,Y相互独立的充要条件是参数ρ（相关系数）=0
※连续型随机变量之和的分布
1.一般地：
卷积公式：
2.其他分布
(1)瑞利分布: X, Y均服从N(0， )则 的概率密度为
(2)Max与Min 分布：（自己推广到n个变量的情况）
(3)若X,Y独立，则Cov(X,Y)=0
(4)Cov(aX,bY)=abCov(X,Y)
(5)Cov( )=Cov( Y)+Cov( )
3.标准化随机变量
4.相关系数
也可写做为X,Y的标准化协随机变量的协方差
性质：(1)
(2)|ρ|=1的充要条件，存在常数a，b(b不等于0)，使P{Y=a+bX}=1即X,Y以概率1线性相关。
2.设 的 和 两个样本，则有：
(1)
5.相关性
对于随机变量X,Y下列结论是等价的：
(1)X与Y不相关 (3)ρ=0 (5)D(X Y)=D(X)+D(Y)
(2)Cov(X,Y)=0 (4)E(XY)=E(X)E(Y)
X,Y相互独立可以推出上述五个结论。
※切比雪夫不等式
表明：对于任意正数ε，当随机变量X的方差越小时，事件 的概率越小，其对立面概率越大。
则
定理(2)X Y相互独立，g(x)和h(y)是两个一元连续函数，则g(X)和h(Y)也相互独立。
定理(3) 则 。且 只差一个常数因子。
(重点)※期望与方差的性质
1期望的性质
(1)一维的：
若Y=g(X),
二维的：
若Z=g(X,Y),
(2)性质：E(C)=C E(CX)=CE(X) (C为常数)
E(X+Y)=E(X)+E(Y)
3.边缘概率密度函数
4.二维正态分布(还是看一下会比较好)
(1)二维正态分布中X,Y相互独立的充要条件是参数ρ（相关系数）=0
※连续型随机变量之和的分布
1.一般地：
卷积公式：
2.其他分布
(1)瑞利分布: X, Y均服从N(0， )则 的概率密度为
(2)Max与Min 分布：（自己推广到n个变量的情况）
(3)若X,Y独立，则Cov(X,Y)=0
(4)Cov(aX,bY)=abCov(X,Y)
(5)Cov( )=Cov( Y)+Cov( )
3.标准化随机变量
4.相关系数
也可写做为X,Y的标准化协随机变量的协方差
性质：(1)
(2)|ρ|=1的充要条件，存在常数a，b(b不等于0)，使P{Y=a+bX}=1即X,Y以概率1线性相关。
概率论乘法公式
设B={零件是乙厂生产}
300个
A={是标准件} 乙厂生产 所求为P(AB).
300个
乙厂生产
189个是
标准件
甲、乙共生产
1000 个
4
设B={零件是乙厂生产} 300个
A={是标准件}
乙厂生产
所求为P(AB) .
若改为“发现它是乙厂生产的, 问它是标准件的概率是多少?”
189个是
标准件
甲、乙共生产
优名酒各一瓶,第 三个拿到两瓶国 优名酒
从而： P (A) B 0 .4C 6 0 .57 3 0 .06 6 0 .0 71
20
例 设某光学仪器厂制造的透镜,第一次落下时 1
打二破 次的 落概 下率破为的概2 率，为若第107 一, 若次前落两下次时落未下打未破打,第 破, 第三次打破的概率为 9
b b c r r c brbrcbr 2 cbr 3 c
当 c>0 时，由于每次取出球后会增加下 一次也取到同色球的概率. 这是一个传染病 模型. 每次发现一个传染病患者，都会增加 再传染的概率.
14
一场精彩的足球赛将要举行，
5个球迷好不容易才搞到一张入场券. 大家都想去,只好用抽签的方法来解决.
第1个人抽到入场券的概率是1/5.
16
由于 A2 A1A2
由乘法公式
因为若第2个人抽到
了入场券，第1个人
P (A 2)P (A 1 )P (A 2|A 1 ) 肯定没抽到.
也就是要想第2个人抽到入场券，必须第1 个人未抽到，
计算得： P(A2)= (4/5)(1/4)= 1/5
17
同理，第3个人要抽到“入场券”，必须 第1、第2个人都没有抽到. 因此
条件概率和概率的乘法公式
一、全概率公式
例
一个盒子中有６只白球、４只黑球，从中不放回 地每次任取１只，连取２次，求第二次取到白球 的概率 A={第一次取到白球} ，且ＡＢ与 A B
解
因为 Ｂ＝ＡＢ∪ A B
互不相容，所以
P ( B ) P ( A B ) P ( A B )
P ( A ) P ( B A ) P ( A ) P ( B A )
P ( A B ) P ( B ) ( B A ) 0 . 8 所求概率为 P P ( A ) P ( A )
甲，乙，丙3人参加面试抽签，每人的试题通过
不放回抽签的方式确定。假设被抽的10个试题签中有4
个是难题签，按甲先，乙次，丙最后的次序抽签。试求
1）甲抽到难题签，2）甲和乙都抽到难题签，3）甲没
B 1 =“第一个是男孩”
于是得
B
1
={(男, 男) , (男 , 女) }
3 1 P B BA P A P 4 4 1 1 P B1 P B P A 1A 2 4
乘法法则
P(AB) P(A)P(B A) P(B)P(A B)
P( AB) P(B A) P( A) P( AB) P( A B) P(B)
解
设从这批种子中任选一颗是一等，二等，三等，四 等种子的事件分别是Ａ1，Ａ2，Ａ3，Ａ4，则它们构 成完备事件组，又设Ｂ表示任选一颗种子所结的穗含 有50粒以上麦粒这一事件，则由全概率公式：
4 i 1
P ( B ) P ( A P ( BA i) i)
＝95.5％×0.5＋2％×0.15＋1.5％×0.1＋1％×0.05 ＝0.4825
贝叶斯公式 Bayes’ Theorem
概率论公式
n
注：如果有 n 个变量服从同一个 0-1 分布， Xi ~ b(1, p) ，则其和 X Xi 服从二项 i
分布 X ~ b(n, p)
11. Poisson 分布
X ~ P() P( X k) k e , k 0,1,...
F
(x)
0, 1,
x x
c c
E(X ) c
Var( X ) 0
9. 二项分布
X ~ b(n, p)
P( X k) Cnk pk (1 p)nk E(X ) np
Var( X ) np(1 p)
10. 二点分布（0-1 分布）
X ~ b(1, p)
P( X x) px (1 p)1x , x 0,1
p(
x)
2
n 2
1 (
n
)
e
x 2
x
n 2
1
,
x
0
2
0, x 0
E(X ) n
Var( X ) 2n
Gamma 分布变为 2 分布：
当 X ~ Ga(,) ，则 2 X ~ Ga(, 1) 2 (2 ) 2
20. 严格单调函数Y g(X )
pY ( y) px[h(x)] | h '(x) |
21. K 阶原点矩和中心矩
k E(X k ) k E( X E( X ))k
中心矩和原点矩关系：
k
k Cik i (i )ki i0
22. 变异系数
Cv
(
X
)
( E(
第一章 第三讲 条件概率、乘法公式、全概率公式
解: 样本空间 S =｛(1,1),(1,2),„,(1,6), (2,1 )„,(2,6)， „，(6,6)｝, B =｛(1,1),(2,2),(3,3),(4,4),(5,5),(6,6)｝, A =｛(1,3)，(2,2)，(3,1)｝, A B =｛(2,2)｝. 于是 P(A|B)= P(AB)/ P(B)=(1/36)/(6/36)=1/6 .
使用全概率公式关键在于寻找另一组形式：
P ( A ) P ( A B ) P ( B ) P ( A B ) P ( B ).
第一章 第三讲 条件概率、乘法公式、全概率公式
例4
设10 件产品中有 3 件不合格品，从中不放
回地取两次，每次一件，求取出的第二件为
注：若 B 已发生，为使 A 也发生，
则此样本点必属于A B ，
B S AB A
B成为了新的样本空间.
第一章 第三讲 条件概率、乘法公式、全概率公式
容易验证，条件概率满足以下性质： 1、对于事件A，有 0≤P(A|B)≤1；
2、对于必然事件S，有P(S |B) =1；
3、若事件A1，A2 ，„，An ，两两互不相容，则有 P(A1∪A2 ∪ „ ∪ An |B)= P(A1|B)+ P(A2|B )+ „ + P (An |B).
问题的提出： 1) 10个人摸彩，有3张中彩. 问：第1个人中彩的概率为多少？ 第2个人中彩的概率为多少？ 2) 10个人摸彩，有3张中彩. 问：已知第1个人没摸中， 第2个人中彩的概率为多少？
第一章 第三讲 条件概率、乘法公式、全概率公式
• 引例 10个产品中有7个正品、3个次品， 从中不放回地抽取两个， 已知第一个取到 次品，求第二个又取到次品的概率.
使用全概率公式关键在于寻找另一组形式：
P ( A ) P ( A B ) P ( B ) P ( A B ) P ( B ).
第一章 第三讲 条件概率、乘法公式、全概率公式
例4
设10 件产品中有 3 件不合格品，从中不放
回地取两次，每次一件，求取出的第二件为
注：若 B 已发生，为使 A 也发生，
则此样本点必属于A B ，
B S AB A
B成为了新的样本空间.
第一章 第三讲 条件概率、乘法公式、全概率公式
容易验证，条件概率满足以下性质： 1、对于事件A，有 0≤P(A|B)≤1；
2、对于必然事件S，有P(S |B) =1；
3、若事件A1，A2 ，„，An ，两两互不相容，则有 P(A1∪A2 ∪ „ ∪ An |B)= P(A1|B)+ P(A2|B )+ „ + P (An |B).
问题的提出： 1) 10个人摸彩，有3张中彩. 问：第1个人中彩的概率为多少？ 第2个人中彩的概率为多少？ 2) 10个人摸彩，有3张中彩. 问：已知第1个人没摸中， 第2个人中彩的概率为多少？
第一章 第三讲 条件概率、乘法公式、全概率公式
• 引例 10个产品中有7个正品、3个次品， 从中不放回地抽取两个， 已知第一个取到 次品，求第二个又取到次品的概率.
概率统计公式大全
概率统计公式大全概率统计是研究随机现象及其规律性的一门学科，其核心就是用数学方法来描述和分析随机现象。
在概率统计的理论体系中，有很多重要的公式和定理，下面对一些常用的公式进行介绍。
1.概率公式：(1)加法规则：P(A∪B)=P(A)+P(B)-P(A∩B)，其中A和B为事件，P(A)和P(B)分别是事件A和事件B发生的概率，P(A∩B)表示事件A和事件B同时发生的概率。
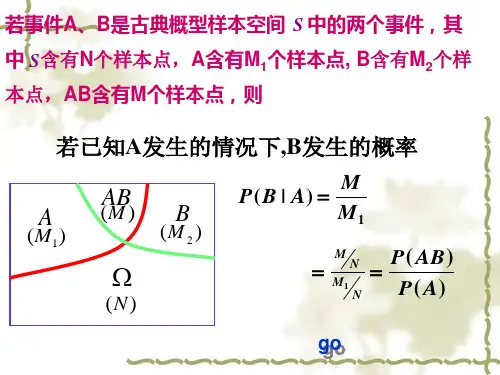
(2)乘法规则：P(A∩B)=P(A)×P(B，A)，其中P(A∩B)表示事件A和事件B同时发生的概率，P(A)表示事件A发生的概率，P(B，A)表示在事件A发生的条件下事件B发生的概率。
2.条件概率公式：(1)贝叶斯定理：P(A，B)=P(B，A)×P(A)/P(B)，其中P(A，B)表示在事件B发生的条件下事件A发生的概率，P(B，A)表示在事件A发生的条件下事件B发生的概率，P(A)和P(B)分别是事件A和事件B发生的概率。
(2)全概率公式：P(B)=ΣP(Ai)×P(B，Ai)，其中B是一个事件，Ai是样本空间的一个划分，即Ai是互不相容且并集为样本空间的一组事件。
3.期望公式：(1) 离散型随机变量的期望：E(X) = ΣxiP(X=xi)，其中X是一个离散型随机变量，xi是X的取值，P(X=xi)是X取值为xi的概率。
(2) 连续型随机变量的期望：E(X) = ∫xf(x)dx，其中X是一个连续型随机变量，f(x)是X的概率密度函数。
4.方差公式：(1) 离散型随机变量的方差：Var(X) = Σ(xi-E(X))^2P(X=xi)，其中Var(X)表示随机变量X的方差，xi是X的取值，E(X)是X的期望，P(X=xi)是X取值为xi的概率。
(2) 连续型随机变量的方差：Var(X) = ∫(x-E(X))^2f(x)dx，其中Var(X)表示随机变量X的方差，E(X)是X的期望，f(x)是X的概率密度函数。
概率论-1-5条件概率,乘法公式,全概率公式,贝叶斯公式
3
P ( B) P ( Ai )P ( B｜Ai )
i 1
1 1 1 2 1 1 8 3 5 3 5 3 15
将此例中所用的方法推广到一般的情形，就 得到在概率计算中常用的全概率公式.
2. 样本空间的划分及全概率公式
定义 设S为试验E的样本空间， B1 B1, B2,, Bn 为E的一组事件，若
注意P(AB)与P(A | B)的区别！ 请看下面的例子
例4 甲、乙两厂共同生产1000个零件，其中 300 件是乙厂生产的. 而在这300个零件中，有189个是标准 件，现从这1000个零件中任取一个，问这个零件是乙厂 生产的标准件的概率是多少？
解 设B={零件是乙厂生产}, A={是标准件}
PBi PA | Bi
i 1
当 n=2 时，划分 B1, B2 可写成划分 B, B ，于是 P( A) P(B)P( A | B) P(B)P( A | B))
3. 全概率公式的理解
n
PA PBi PA | Bi
i 1
全概率公式 .
全概率公式的基本思想 是把一个未知的复杂事 件
样本空间中的任一事件 A ,恒有
n
PA PBi PA | Bi
i 1
证明 因为 A AS AB1 B2 Bn
AB1 AB2 ABn
并且 ABi AB j , i j ,所以
PA PAB1 PAB2 PABn
P n
B1
P
A
|
B1
PBn PA | Bn
解 记 Ai={球取自i号箱}, i=1,2,3;
B ={取得红球}
12 3
其中 A1、A2、A3两两互斥 B发生总是伴随着A1，A2，A3 之一同时发生，
P ( B) P ( Ai )P ( B｜Ai )
i 1
1 1 1 2 1 1 8 3 5 3 5 3 15
将此例中所用的方法推广到一般的情形，就 得到在概率计算中常用的全概率公式.
2. 样本空间的划分及全概率公式
定义 设S为试验E的样本空间， B1 B1, B2,, Bn 为E的一组事件，若
注意P(AB)与P(A | B)的区别！ 请看下面的例子
例4 甲、乙两厂共同生产1000个零件，其中 300 件是乙厂生产的. 而在这300个零件中，有189个是标准 件，现从这1000个零件中任取一个，问这个零件是乙厂 生产的标准件的概率是多少？
解 设B={零件是乙厂生产}, A={是标准件}
PBi PA | Bi
i 1
当 n=2 时，划分 B1, B2 可写成划分 B, B ，于是 P( A) P(B)P( A | B) P(B)P( A | B))
3. 全概率公式的理解
n
PA PBi PA | Bi
i 1
全概率公式 .
全概率公式的基本思想 是把一个未知的复杂事 件
样本空间中的任一事件 A ,恒有
n
PA PBi PA | Bi
i 1
证明 因为 A AS AB1 B2 Bn
AB1 AB2 ABn
并且 ABi AB j , i j ,所以
PA PAB1 PAB2 PABn
P n
B1
P
A
|
B1
PBn PA | Bn
解 记 Ai={球取自i号箱}, i=1,2,3;
B ={取得红球}
12 3
其中 A1、A2、A3两两互斥 B发生总是伴随着A1，A2，A3 之一同时发生，
大学概率论之条件概率,乘法公式
2
Ch2
定义
设 A, B 是两个事件, 且 P( A) 0, 称 P( AB) P( B A) P( A)
为事件 A 发生的条件下事件 B 发生的概率， 简称B对A的条件概率. P( AB) 同理可得
P( A B)
P(B)
为事件 B 发生的条件下事件 A发生的概率， 简称A对B的条件概率.
Ch2
条件概率 P(B|A) 的计算
1) 缩减样本空间： 将 缩减为A=A， 采用古典概型来计算.
P( AB ) 2) 用定义： P ( B A ) P ( A)
( ) 与 概 率 P （ A B ) 条件概率PBA 有何不同 ?
Ch2
条件概率P(B|A) 中，A与B地位不同，且已知A 已发生作为条件。在概率P(AB）中，A，B同时 发生，地位相同。在应用时必须区别是 PBA ( )还 是 P （ A B ) 例如从6个正品2个次品的袋中，无放回抽 取2次，一次取一个。A={第一次为正品}， B={第二次为次品}，求（1）第二次才取 到次品的概率（2）已知第一次取到正品， B发生的概率。
n 1
条件概率与乘法公式
有二个箱子,分别编号为1,2. 1号箱装有1个红球4 个白球,2号箱装有2红3白球. 某人从1号箱中任取一 球放入2号箱,再从2号箱中任意摸出一球, 求已知从1号箱取出白球的条件下从2号箱取得红球 的概率.
Ch2
记 A={从1号箱取得白球},
B ={从2号箱取得红球}
1
Ch2
用乘法公式容易求出 P(W1W2R3R4) =P(W1)P(W2|W1)P(R3|W1W2)P(R4|W1W2R3)
b bc r r c br br c br 2 c br 3 c
条件概率乘法公式
即 若P(B)>0,则P(AB)=P(B)P(A|B) (2)
将A、B的位置对调，有
若 它们(P2(可)A和)计>(30算),则式两P都个(B称事A为)件=乘P同(法A时)公P发(式B生|A,的) 利概用率 而 P(AB)=P(BA)
故 P(A)>0,则P(AB)=P(A)P(B|A) (3)
注意P(AB)与P(A | B)的区别！ 请看下面的例子
A={取到一等品}， B={取到正品} P(A )=3/10， P(A|B) 3 3 10 P( AB)
7 7 10 P(B)
A={取到一等品}，B={取到正品}
P(A )=3/10， P(A|B)=3/7 本例中，计算P(A)时，依
据的前提条件是10件产品中一 等品的比例.
计算P(A|B)时，这个前提条件未变，只 是加上“事件B已发生”这个新的条件.
P(A|B) P(A)?
或 P(A|B) P(A)?
请思考！！
推广到多个事件的乘法公式:
当P(A1A2…An-1)>0时，有 P (A1A2…An） =P(A1)P(A2|A1) …P(An| A1A2…An-1)
乘法公式应用举例 （波里亚罐子模型）
b个白球, r个红球
一个罐子中包含b个白球和r个红球. 随机地抽取一个球，观看颜色后放回罐中， 并且再加进c个与所抽出的球具有相同颜 色的球. 这种手续进行四次，试求第一、 二次取到白球且第三、四次取到红球的概 率.
一、条件概率
1. 条件概率的概念
在解决许多概率问题时，往往需要在 有某些附加信息(条件)下求事件的概率. 如在事件B发生的条件下求事件A发生的 概率，将此概率记作P(A|B).
一般 P(A|B) ≠ P(A)
条件概率与乘法公式
84
例2 从混有5张假钞的20张百元钞票中任 意抽出2张, 将其中1张放到验钞机上检验 发现是假钞. 求2 张都是假钞的概率.
下面两种解法哪个正确？
解一 令 A 表示 “其中1张是假钞”. B表示 “2 张都是假钞”
由缩减样本空间法得
P A B 4 /19 0.2105.
85
乘法公式 利用条件概率求积事件的概率即乘法公式
79
§1.3 条件概率
条件概率与乘法公式
引例 袋中有7只白球, 3只红球, 白球中
有4只木球, 3只塑料球; 红球中有2只木球, 1只塑料球.
现从袋中任取1球, 假设每个球被取到 的可能性相同. 若已知取到的球是白球, 问 它是木球的概率是多少？ 古典概型
设 A 表示任取一球，取得白球； B 表示任取一球，取得木球.
83
条件概率也是概率, 故具有概率的性质：
非负性 归一性 可列可加性
P(B A) 0
P( A) 1
P
i1
Bi
A
P
i1
Bi
A
P(B1 B2 A) P(B1 A) P(B2 A) P(B1B2 A)
P(B A) 1 P(B A)
P(B1 B2 A) P(B1 A) P(B1B2 A)
解 令 A 灯泡能用到1000小时 B 灯泡能用到1500小时
所求概率为
PB A P(AB) P(B) 0.4 1
P(A) P( A) 0.8 2
B A
87
例2 从混有5张假钞的20张百元钞票中任 意抽出2张, 将其中1张放到验钞机上检验 发现是假钞. 求2 张都是假钞的概率.
下面两种解法哪个正确？
kA 7 /10 n
大学概率论必背公式
数学期望、方差、协方差等都是一些特殊的矩。
五、样本及抽样分布
1、常用统计量 （1）样本均值（样本平均数）
（2）样本方差
（3）k 阶样本矩
2、抽样分布 统计量的分布称为抽样分布。 （1） 2—分 布
性质： A. 可加性 若1 ~ 2(n1)，2~ 2(n2 )，1， 2 独立，则1 + 2 ~ 2(n1+n2 )。 B. 期望与方差 若 ~ 2(n)，则 E()= n，D()=2n。 （2）t—分布 若 ~ N(0, 1), ~ 2(n), 与独立，则
8、相关系数： 若 r.v. X，Y 的方差和协方差均存在, 且 D(X )> 0, D(Y )> 0，则
称为 X 与 Y 的相关系数. X 与 Y 不相关 Cov(X, Y )=0 E(XY )= E(X )E (Y )。
8、矩 （1）k 阶原点矩 E(X k ), k=1, 2, … 而 E(|X|k)称为 X 的 k 阶绝对原点矩； （2）k 阶中心矩 E[XE(X )]k, k=1, 2, … 而 E|X-E(X )|k 称为 X 的 k 阶绝对中心矩；
称 X 服从参数为 p 的几何分布。 （3）二项分布 ( B(n, p) ) 以 X 记 n 重贝努里试验中 A 发生的次数，则其分布率为：
P( X k) C k p k (1 p)nk , (k 0,1, , n) n 称 X 服从参数为(n，p)的二项分布，记为 X~B(n，p)
（4）泊松(Poisson)分布 ( P() ) 若随机变量 X 的所有取值为一切非负整数，且其分布律为：
5. 边缘分布 6. 二维连续型随机变量及其密度函数 联合密度 f (x , y )的性质
7. 边缘密度函数
概率论 第四节条件概率 全概率公式
乙、丙三个厂中哪个厂生产的可能性大？
解 设事件A表示“取到的产品为正
B1, B2品, B”3 分，别表示“产品由甲、乙、丙厂生产”
由已知 P(B1 ) 0.2, P(B2 ) 0.3, P(B3 ) 0.5
P( A B1 ) 0.95, P( A B2 ) 0.9, P( A B3 ) 0.8
当有了新的信息（知道B发生），人们对
诸事件发生可能性大小P(Ai|B)有了新的估计。 贝叶斯公式从数量上刻划了这种变化。
例8 同一种产品由甲、乙、丙三个厂供应。 由长期的经验知，三家的正品率分别为0.95、 0.90、0.80，三家产品数所占比例为2:3:5，混 合在一起。
（1）从中任取一件，求此产品为正品的概率； （2）现取到一件产品为正品，问它是由甲、
我们也称A ，B，C 是相互独立的事件。 定理 若事件A与B是相互独立的，则
A与B ,A与 B , A与 都B 是相互独立的。
例 3 一个均匀的正四面体,将第一面染成
红色,第二面染成白色,第三面染成黑色,第四
面同时染上红、白、黑三种颜色，如果以A、
B、C分别表示投掷一次正四面体时红、白、
黑颜色着地的事件，由于在四个面中两面上
冒病毒是相互独立的，则所求概率为
P1500 Ai 1 PA1A2 A1500
i1
1 PA1PA2 PA1 1 1 0.002 1500 1 e1500 ln 10.002
1 e15000.002 1 e3 0.95
从这个例子可见，虽然每个带有感冒病 毒的可能性很小，但许多聚集在一起时空气 中含有感冒病毒的概率可能会很大，这种现 象称为小概率事件的效应。卫生常识中,不让 婴儿到人多的公共场所去就是这个道理。
条件概率与乘法公式
很明显这张卡片不可能是黑点---黑点卡，因此，它要 么是圆圈---圆圈卡，要么是黑点---圆圈卡，二者必居 其一，这样一来，这张卡片的背面不是黑点，就是圆 圈，所以赌什么都一样，全是公平的，你和我赢的机 会均等，都是。
让我们看看问题出在哪里？？
我千方百计要你相信的是，同样可能发生的情况只有两种。然 而事实是，同样可能发生的情况有三种
（2）样本空间不同，在P(A|B)中，事件B成为样本
空间；在P（AB）中，样本空间仍为 。
因而有 P(A B) P(AB)
例 设 100 件产品中有 70 件一等品，25 件二等品，
规定一、二等品为合格品．从中任取1 件，求 (1) 取得 一等品的概率；(2) 已知取得的是合格品，求它是一等 品的概率．
解 设Ａ表示取到的产品是一等品，Ｂ表示取
出的产品是合格品， 则
P(A | B) 45%
P(B ) 4%
于是 P(B) 1 P(B ) 96%
所以 P(A) P(AB) P(B)P(A | B)
96%45% 43.2%
一个盒子中有６只白球、４只黑球，从中不放回地 每次任取１只，连取２次，求 (1) 第一次取得白球的概 率； (2) 第一、第二次都取得白球的概率； (3) 第一次取 得黑球而第二次取得白球的概率．
条件概率 P(A|B)的样本空间
BA
BA
Sample space
P( AB)
Reduced sample space given event B
P(A | B)
概率 P(A|B)与P(AB)的区别与联系
联系：事件A，B都发生了 区别： （1）在P(A|B)中，事件A，B发生有时间上的差异， B先A后；在P（AB）中，事件A，B同时发生。
让我们看看问题出在哪里？？
我千方百计要你相信的是，同样可能发生的情况只有两种。然 而事实是，同样可能发生的情况有三种
（2）样本空间不同，在P(A|B)中，事件B成为样本
空间；在P（AB）中，样本空间仍为 。
因而有 P(A B) P(AB)
例 设 100 件产品中有 70 件一等品，25 件二等品，
规定一、二等品为合格品．从中任取1 件，求 (1) 取得 一等品的概率；(2) 已知取得的是合格品，求它是一等 品的概率．
解 设Ａ表示取到的产品是一等品，Ｂ表示取
出的产品是合格品， 则
P(A | B) 45%
P(B ) 4%
于是 P(B) 1 P(B ) 96%
所以 P(A) P(AB) P(B)P(A | B)
96%45% 43.2%
一个盒子中有６只白球、４只黑球，从中不放回地 每次任取１只，连取２次，求 (1) 第一次取得白球的概 率； (2) 第一、第二次都取得白球的概率； (3) 第一次取 得黑球而第二次取得白球的概率．
条件概率 P(A|B)的样本空间
BA
BA
Sample space
P( AB)
Reduced sample space given event B
P(A | B)
概率 P(A|B)与P(AB)的区别与联系
联系：事件A，B都发生了 区别： （1）在P(A|B)中，事件A，B发生有时间上的差异， B先A后；在P（AB）中，事件A，B同时发生。
概率论乘法公式
概率论乘法公式乘法公式是概率论中用于计算复合事件概率的重要工具。
它描述了当两个或多个事件依次发生时，整个事件的概率如何计算。
乘法公式的具体表达式如下：P(A and B) = P(A) * P(B，A)其中，P(A and B)表示事件A和事件B同时发生的概率，P(A)表示事件A发生的概率，P(B，A)表示在事件A发生的条件下，事件B发生的概率。
乘法公式可以推广到多个事件的情况。
假设有n个事件A1,A2,...,An，它们依次相互独立地发生的概率可以使用乘法公式计算：P(A1 and A2 and ... and An) = P(A1) * P(A2，A1) * P(A3，A1 and A2) * ... * P(An，A1 and A2 and ... and An-1)乘法公式的应用非常广泛。
它可以用于计算一系列相互独立事件的概率，也可以用于计算多次试验的概率。
下面通过一些具体的例子来说明乘法公式的应用。
例1：有一批产品中，20%是次品。
现从该批产品中连续取两个，求两个产品都是次品的概率。
解：令A为第一个产品是次品的事件，B为第二个产品是次品的事件。
题目要求求解P(A and B)。
已知P(A) = 0.2，求解P(B，A)。
由于取出第一个产品后，第二个产品的选择不受第一个产品的影响，所以第一个产品是次品的事件A对于第二个产品是次品的事件B是独立的。
因此，P(B，A)=P(B)=0.2带入乘法公式，可得：P(A and B) = P(A) * P(B，A) = 0.2 * 0.2 = 0.04所以两个产品都是次品的概率为0.04例2：地区一年中每月的天气情况分为晴天、阴天和雨天。
已知当一个月是晴天的概率是0.6，阴天的概率是0.3，雨天的概率是0.1、现在假设每个月的天气情况相互独立，求连续2个月都是阴天的概率。
解：令A为第一个月是阴天的事件，B为第二个月是阴天的事件。
题目要求求解P(A and B)。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
记 A={从1号箱取得白球},
B ={从2号箱取得红球}
12
Ch2
定义
设 A, B 是两个事件,且 P( A) 0, 称 P(B A) P( AB) P( A)
为事件 A 发生的条件下事件 B 发生的概率，
简)
为事件 B 发生的条件下事件 A发生的概率， 简称A对B的条件概率.
Ch2
用乘法公式容易求出 P(W1W2R3R4) =P(W1)P(W2|W1)P(R3|W1W2)P(R4|W1W2R3)
b bc r rc brbrcbr2 cbr3 c
当 c > 0 时，由于每次取出球后会增加下一次 也取到同色球的概率. 这是一个传染病模型. 每次 发现一个传染病患者，都会增加再传染的概率.
Ch2
条件概率 P(B|A) 的计算
1) 缩减样本空间： 将 缩减为A=A， 采用古典概型来计算.
2) 用定义： P ( B A) P ( A B )
P ( A)
Ch2
条件概率P(BA)与概率P （AB)有何不同?
条件概率P(B|A) 中，A与B地位不同，且已知A 已发生作为条件。在概率P(AB）中，A，B同时 发生，地位相同。在应用时必须区别是 P(BA)还是P（AB)
Ch2
乘法公式应用举例
波里亚罐子模型
b个白球, r个红球
一个罐子中包含b个白球和r个红球. 随机地 抽取一个球，观看颜色后放回罐中，并且再加进 c 个与所抽出的球具有相同颜色的球. 这种手续进行 四次 ，试求第一、二次取到白球且第三、四次取 到红球的概率.
例如从6个正品2个次品的袋中，无放回抽 取2次，一次取一个。A={第一次为正品}， B={第二次为次品}，求（1）第二次才取 到次品的概率（2）已知第一次取到正品， B发生的概率。
Ch2
性质
条件概率是概率
(1 )非: 负 P (B A 性 )0 ;
( 2 )规 范 性 :P ( A ) 1 ,P ( A ) 0 ;
P A1A2A3 P A 1 P A 2 |A 1 P A 3 |A 1 A 2
11 211701190
3 200
.
Ch2
波里亚罐子(传染病）模型
b个白球, r个红球
一个罐子中包含b个白球和r个红球. 随机地抽取 一个球，观看颜色后放回罐中，并且再加进 c 个 与所抽出的球具有相同颜色的球. 这种手续进行四 次 ，试求第一、二次取到白球且第三、四次取到 红球的概率.
解：设 A = {活 20 岁以上} ， B = {活 25 岁以上}
则有P(BA)P(AB). P(A)
因P 为 (A )0.8, P(B)0.4, P (A) B P (B ), 所以 P(BA)P(AB) 0.4 1.
P(A) 0.8 2
Ch2
乘法公式
利用条件概率求积事件的概率即乘法公式
Ch2
随机取一个球，观看颜色后放 回罐中，并且再加进c个与所抽出
的球具有相同颜色的球.
b个白球, r个红球 解 设 Wi={第i次取出是白球}, i=1,2,3,4
Rj={第j次取出是红球}， j=1,2,3,4 于是W1W2R3R4表示事件“连续取四个球，第一、 第二个是白球，第三、四个是红球. ”
例1 盒中装有5个产品, 其中3个一等品，2个Ch2 二等品, 从中不放回地取产品, 每次1个, 已知 第一次取得一等品，求第二次取得的是二等 品的概率.
解
令
Ai={第
i次取到一等品}， A1
P A2
A1
1 2
（1）
Ch2
例2 某种动物由出生算起活20岁以上的概率为 0.8, 活到25岁以上的概率为0.4, 如果现在有一只 20岁的这种动物, 问它能活到25岁以上的概率是 多少?
（1）
C
（也可直接按古典概型算
1 3
C
1 2
)
C 1C 1
Ch2
( 2 ) P ( A 1A 2 A 3 ) P A 1 P A 2A 1 P A 3A 1 A 2 (2) 213 1 15310430.5 10 3 5
Ch2
例 4 设 某 光 学 仪 器 厂 制 造 的 透 镜 , 第 一 次 落 下 时
打破的1,概 若率 第为 一次,落 第下 二未 次打 落 2
打破的 7,若 概前 率两 是,第 次三 未次 打落 破 破的概9率 1 ,试 0是 求透镜落破 下的 三概 .次率 未
10
解 设 A i透 镜 第 i次 落 下 打 破 ,i1,2,3,
则 A i透 镜 第 i次 落 下 未 打 破 ,i1,2,3,
乘法公式主要用于求几个事件同时发生的概率.
Ch2
例3 盒中装有5个产品, 其中3个一等 品，2个二等品, 从中不放回地取产品, 每次 1个, 求 （1）取两次，两次都取得一等品的概率;
（2）取三次，第三次才取得一等品的概率;
解 令 Ai ={第 i 次取到一等品}
(1 )P (A 1 A 2)P (A 1 )P (A 2A 1 )5 34 2 1 3 0
(1) 若 P(B)>0，则 P(AB) = P(B)P(A|B)； 若 P(A)>0，则 P(AB) = P(A)P(B|A).
(2) 若 P(A1A2 ······An1)>0，则 P(A1A2 ······An) = P(A1)P(A2|A1) ······P(An|A1A2 ······An1)
(3 )可 列 可 加 性 :设 B 1 ,B 2 , 是 两 两 互 斥 的 事
件 ,则 有
PBi AP(Bi A).
i1
i1
(4)P(BA)1P(B|A).
( 5 )P [ ( B 1 B 2 ） A ] P [ ( B 1 B 2 ） A ] P ( B 1 A ) P ( B 1 B 2 A ) ;
Ch2
条件概率与乘法公式
问题的提出：
1) 共n张彩票，有3张中彩.
3
问： 第2个人中彩的概率为多少？ n
2) 共n张彩票，有3张中彩.
问：已知第l个人摸中，则 第2个人中彩的概率为多少？ 2
n 1
Ch2
条件概率与乘法公式
有二个箱子,分别编号为1,2. 1号箱装有1个红球4 个白球,2号箱装有2红3白球. 某人从1号箱中任取一 球放入2号箱,再从2号箱中任意摸出一球, 求已知从1号箱取出白球的条件下从2号箱取得红球 的概率.