2.2.1综合法和分析法ppt课件

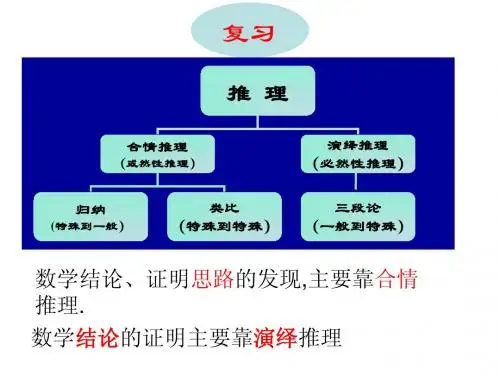
§2.2 直接证明与间接证明 2．2.1 综合法和分析法(一)课时目标 1.了解直接证明的两种基本方法——分析法和综合法.2.理解分析法和综合法的思考过程、特点，会用分析法和综合法证明数学问题．综合法分析法定义利用__________和某些数学______、______、______等，经过一系列的____________，最后推导出所要证明的结论成立，这种证明方法叫做综合法从要证明的______，逐步寻求使它成立的____________，直至最后，把要证明的结论归结为判定一个明显成立的条件(已知条件、______、______、______等)，这种证明方法叫做分析法框图表示 P ⇒Q 1→Q 1⇒Q 2→Q 2⇒Q 3→…→Q n ⇒Q (P 表示________、已 有的______、______、 ______等，Q 表示 ________________) Q ⇐P 1→P 1⇐P 2→ P 2⇐P 3→…→ 得到一个明显成立的条件特点顺推证法或由因导果法逆推证法或执果索因法一、选择题1．已知x ≥52，则f (x )＝x 2－4x ＋52x －4有( )A ．最大值54B ．最小值54C ．最大值1D ．最小值12．命题“对于任意角θ，cos 4θ－sin 4θ＝cos 2θ”的证明：“cos 4θ－sin 4θ＝(cos 2θ－sin 2θ)(cos 2θ＋sin 2θ)＝cos 2θ－sin 2θ＝cos 2θ”过程应用了( )A ．分析法B ．综合法C ．综合法、分析法综合使用D ．间接证法3．如果x >0，y >0，x ＋y ＋xy ＝2，则x ＋y 的最小值是( )A ．32B ．23－2C ．1＋ 3D ．2－ 34．要证明a ＋a ＋7<a ＋3＋a ＋4 (a ≥0)可选择的方法有多种，其中最合理的是( )A ．综合法B ．类比法C ．分析法D ．归纳法5．已知实数a ，b ，c 满足a ＋b ＋c ＝0，abc >0，则1a ＋1b ＋1c的值( )A ．一定是正数B ．一定是负数C ．可能是零D ．正、负不能确定二、填空题6．设a ＝3＋22，b ＝2＋7，则a 、b 的大小关系为________．7．已知a 、b 、u ∈R *，且1a ＋9b＝1，则使得a ＋b ≥u 恒成立的u 的取值范围是__________．8．设a ＝2，b ＝7－3，c ＝6－2，则a ，b ，c 的大小关系为__________．三、解答题9．已知a >0，b >0，求证：b 2a ＋a 2b≥a ＋b .10．已知a ，b ，c ，d ∈R ，求证：ac ＋bd ≤(a 2＋b 2)(c 2＋d 2).能力提升11．a >b >c ，n ∈N *，且1a －b ＋1b －c ≥na －c恒成立，则n 的最大值为________．12．已知a >0，b >0，用两种方法证明：a b ＋ba≥a ＋b .1．运用综合法解题时，要保证前提条件正确，推理要合乎逻辑规律，只有这样才能保证结论的正确性．2．在分析法证明中，从结论出发的每一个步骤所得到的判断都是使结论成立的充分条件．最后一步归结到已被证明了的事实．因此，从最后一步可以倒推回去，直到结论，但这个倒推过程可以省略．§2.2 直接证明与间接证明 2．2.1 综合法和分析法(一)答案综合法 分析法定利用已知条件和某些数学定义、定理、从要证明的结论，逐步寻求使它成立的充分条1．D [f (x )＝x －22＋12(x －2)∵x －2≥12，∴f (x )≥2·x －22×12(x －2)＝1.当x ＝3时，f (x )min ＝1.]2．B [从证明的过程来看是从已知条件入手经过推导得到结论，符合综合法．] 3．B [由x >0，y >0，x ＋y ＋xy ＝2，则2－(x ＋y )＝xy ≤⎝⎛⎭⎫x ＋y 22， ∴(x ＋y )2＋4(x ＋y )－8≥0，∴x ＋y ≥23－2或x ＋y ≤－2－2 3.∵x >0，y >0，∴x ＋y 的最小值为23－2.] 4．C [要证a ＋a ＋7<a ＋3＋a ＋4， 只要证a ＋a ＋7＋2a (a ＋7) <a ＋3＋a ＋4＋2(a ＋3)(a ＋4)， 只要证a 2＋7a <a 2＋7a ＋12， 只要证a 2＋7a <a 2＋7a ＋12， 只要证0<12.由此可知，最合理的是分析法．]5．B [∵a ＋b ＋c ＝0，∴(a ＋b ＋c )2＝0， ∴a 2＋b 2＋c 2＋2(ab ＋bc ＋ac )＝0，∴ab ＋bc ＋ac ＝－12(a 2＋b 2＋c 2)<0.又abc >0，∴1a ＋1b ＋1c ＝ab ＋bc ＋acabc<0.]6．a <b解析 a ＝3＋22，b ＝2＋7两式的两边分别平方，可得a 2＝11＋46，b 2＝11＋47，明显6<7，故a <b .7．(－∞，16]解析 ∵a ＋b ＝(a ＋b )⎝⎛⎭⎫1a ＋9b＝10＋b a ＋9a b ≥10＋2b a ×9a b ＝16，当且仅当b a ＝9ab即3a ＝b 时取等号，若a ＋b ≥u 恒成立，则u ≤16. 8．a >c >b解析 b ＝47＋3，c ＝46＋2，显然b <c . 而a 2＝2，c 2＝8－212＝8－48 <8－36＝2＝a 2， ∴a >c .9．证明 ∵b 2a ＋a 2b ＝a 3＋b3ab＝(a ＋b )(a 2－ab ＋b 2)ab，又∵a >0，b >0，∴a 2－ab ＋b 2－ab ＝(a －b )2≥0，∴a 2－ab ＋b 2≥ab ，∴a 2－ab ＋b 2ab≥1，∴(a ＋b )·a 2－ab ＋b 2ab≥a ＋b .∴b 2a ＋a 2b≥a ＋b . 10．证明 ①当ac ＋bd ≤0时，显然成立． ②当ac ＋bd >0时，欲证原不等式成立， 只需证(ac ＋bd )2≤(a 2＋b 2)(c 2＋d 2)．即证a 2c 2＋2abcd ＋b 2d 2≤a 2c 2＋a 2d 2＋b 2c 2＋b 2d 2. 即证2abcd ≤b 2c 2＋a 2d 2. 即证0≤(bc －ad )2.因为a ，b ，c ，d ∈R ，所以上式恒成立． 故原不等式成立，综合①、②知，命题得证． 11．4解析 ∵a >b >c ，∴a －b >0，b －c >0，a －c >0.若1a －b ＋1b －c ≥n a －c 恒成立， 即a －c a －b ＋a －c b －c≥n 恒成立． a －c a －b ＋a －c b －c ＝a －b ＋b －c a －b ＋a －b ＋b －cb －c ＝2＋b －c a －b ＋a －b b －c ≥2＋2b －c a －b ·a －b b －c ＝4.∴当且仅当a －b ＝b －c 时取等号． ∴n 的最大值为4.12．证明 方法一 (综合法)： 因为a >0，b >0，所以a b ＋ba －a －b＝⎝⎛⎭⎫a b －b ＋⎝⎛⎭⎫ba －a ＝a －b b ＋b －aa＝(a －b )⎝⎛⎭⎫1b －1a＝(a －b )2(a ＋b )ab ≥0，所以a b ＋ba≥a ＋b .方法二(分析法)：要证ab＋ba≥a＋b，只需证a a＋b b≥a b＋b a，即证(a－b)(a－b)≥0，因为a>0，b>0，a－b与a－b同号，所以(a－b)(a－b)≥0成立，所以ab＋ba≥a＋b成立．。