求解超静定刚架的一种新方法

建筑力学基本计算5力法计算一次超静定结构1、基本概念和计算要求在学习力法计算超静定结构的时候,要注意下列几点：1） 力法的基本原理，通过多余未知力的概念，把超静定结构问题转化为静定结构的计算问题。

2） 结构超静定次数的确定，多余约束、多余约束反力和抄静定次数的关系，基本结构的确定。

3） 力法典型方程的建立及方程中想关系数的意义。

2、基本计算方法在学习力法的基本方法时，要注意下列问题：1） 选择基本结构。

由于力法是以多余未知力作为基本未知量，首先应根据去掉多余约束的原则和方法去掉多余约束代之以多余未知力，得到与原结构相应的静定结构即基本结构。

选择基本结构应注意：基本结构必须是几何不变体系的静定结构，几何可变体系（或瞬变体系）不能用作基本结构；多余约束力的方向应该符合约束的方向；选择的基本结构应该尽量使解题步骤简化。

2） 基本方程的建立。

将基本结构与原结构以受力条件进行比较会发现：只要多余未知力就是原结构的支座反力，则基本结构与原结构受力情况完全一致；当解出多余未知力，将其视为荷载加在基本结构上，超静定结构的计算即转化为静定结构的计算。

3、计算步骤和常用方法考试要求基本是以力法计算一次超静定刚架（或梁）为主，基本计算步骤是：1） 选择基本结构。

确定超静定结构的次数，去掉多余约束，并以相应的约束力代替而得到的一个静定结构作为基本结构。

2）建立力法典型方程。

01111=∆+P X δ（一次超静定结构） 3） 计算δ11和Δ1P 。

首先要画出基本结构在荷载作用下的M P 图和基本结构在单位未知力作用下的1M 图，然后用图乘法分别计算δ11（1M 图和1M 图图乘）和Δ1P （M P 图和1M 图图乘）。

4）求多余未知力。

代入力法典型方程求出多余未知力。

5） 作内力图（一般为作弯矩图）。

可按P M X M M +⋅=11式叠加对应点的弯矩，从而画出弯矩图。

4、举例作图（a ）所示超静定刚架的弯矩图。

已知刚架各杆EI 均为常数。

力法求解超静定结构的步骤篇一《力法求解超静定结构的步骤》我有一个朋友叫小李，他是个建筑系的学生。

有一天，我去他宿舍玩，一进门就看到他对着一堆建筑图纸愁眉苦脸的。

“怎么啦，小李？看起来像是被什么大怪兽给难住了。

”我打趣地问。

小李无奈地指了指图纸说：“你看，这是个超静定结构的设计，要用力法求解，我感觉自己像是在迷宫里转晕了的小老鼠，完全摸不着头脑。

”我拉过一把椅子坐在他旁边，笑着说：“那你给我讲讲这个超静定结构是怎么回事呗，说不定我这个外行人还能给你点灵感呢。

”小李坐直了身子，开始解释：“超静定结构啊，就像是一个复杂的拼图，它的约束比维持稳定所需要的最少约束还多。

你看这个建筑框架，那些多余的约束就像是额外的枷锁，让我们很难直接算出它的内力和变形。

”“那这个力法又是怎么个解法呢？”我好奇地追问。

小李深吸一口气，开始讲述力法求解超静定结构的步骤。

“首先啊，第一步是确定基本结构。

这就好比是给这个复杂的拼图找一个基础框架。

我们要去掉多余的约束，把超静定结构变成静定结构。

比如说这个建筑框架里，可能有些支撑是多余的，我们就想象把它们去掉，但是呢，要在去掉的地方加上相应的未知力，这些未知力就像是代替那些多余约束的小助手。

”他一边说一边在纸上画着简单的草图，“然后第二步，就是根据变形协调条件列出力法方程。

这一步可关键了，就像在搭积木，每一块都要严丝合缝。

变形协调就是说结构在受力之后，各个部分的变形要符合一定的规则。

比如说一根梁在受到压力和拉力的时候，它的弯曲和拉伸变形要在整体结构里是协调的，不能自己各玩各的。

这个时候，我们就要利用结构力学的知识，把各个部分的变形关系找出来，然后列出方程。

这个方程里就包含我们之前设的那些未知力。

”小李越讲越兴奋，手不停地比划着，“第三步呢，就是求柔度系数和自由项。

这就像是给我们之前列的方程找各种零部件。

柔度系数就是结构在单位力作用下的变形，这个得通过各种计算方法来确定。

自由项呢，是结构在荷载作用下的已知变形。

第八章超静定结构解法
超静定结构是指结构中的节点数超过了杆件数，即结构中的自由度超过了平衡条件的数量。

对于超静定结构的解法，需要进行位移计算和支反力计算。

位移计算可以通过以下步骤进行：
1.建立结构的刚度方程。

根据杆件的刚度和支座的自由度约束，可以建立结构的刚度矩阵。

刚度矩阵是一个n×n的矩阵，其中n是结构的自由度数量。

2.确定约束条件。

根据结构的支座约束，可以确定支座位移为零的约束条件。

3.应用边界条件。

将约束条件应用到刚度方程中，可以得到一个未知位移的方程组。

4.解未知位移。

通过解这个方程组，可以得到结构的未知位移值。

支反力计算可以通过以下步骤进行：
1.利用位移计算中得到的未知位移值，计算杆件的应力。

应力可以通过应变和材料的本构关系得到。

2.根据杆件的几何特征和应力，计算杆件的应力。

应力可以根据杆件的截面积和应力得到。

3.根据杆件的几何特征和应力，计算杆件的内力。

内力可以根据截面受力平衡的条件得到。

4.根据内力和支座约束，计算支座的反力。

反力可以通过力的平衡条件得到。

总的来说，超静定结构的解法需要进行位移计算和支反力计算。

在位移计算中，需要建立结构的刚度方程，并将约束条件以及边界条件应用到方程中，来解未知位移。

在支反力计算中，需要利用位移计算中得到的未知位移值，计算杆件的应力和内力，并根据杆件的几何特征和应力来计算支座的反力。

超静定结构用铰化法求解姓名：班级：学号：摘要：利用铰化法解超静定刚架是一种将超静定结构转化为铰化结构求解内力的一种方法。

叙述了将超静定结构转化为铰化结构的依据、转化过程，并推求了部分刚架弯矩为零的截面位置系数，举例说明了铰化法的应用。

关键词：超净定结构；铰化法；铰化结构；铰化图引言超静定结构转化为铰化结构的依据有中间铰的刚架结构受荷载作用时，在中间铰处弯矩等于零；相反，刚架上不是铰连接且弯矩等于零的截面均可以在计算内力时看成是用铰连接。

把超静定结构上弯矩为零的截面改为铰连接的结构称为铰化结构。

对于超静定刚架来说，在某种荷载作用下，只要把弯矩为零的截面位置确定下来，就可以把超静定刚架转化为铰化结构而求解内力。

而铰化结构恰好又能利用解静定结构的方法求解内力，尤其是水平荷载作用下的门字形超静定刚架，无论有几层，其铰化结构均符合几何不变体系的组成规律，没有多余联系，是一个静定结构，因而可以使计算简化。

1 超静定结构转化为铰化结构的途径借用力法的计算结果，根据内力图确定弯矩为零的截B C面位置将杆件从整体中取出来，标出内力及荷载，设某端到弯矩为零的截面距离为，列出截面的弯矩方程，并令其等于零，便可以求出值，即为弯矩等于零的截面位置。

例如，一超静定刚架如图1所示，需确定弯矩为零的截面位置。

解法：取出杆件AB，标出内力及外力，设A端到弯矩为零的截面距离为x，如图2所示。

列出求x截面弯矩方程，并令其等于零：解得：x=0．394L即AB杆弯矩为零的截面在 x=0．394L处,该截面位置系数a1为0．394。

以同样的方法推得BC杆 a2=0．402，CD杆a3 =0．5902．将结构铰化把弯矩为零的截面化为铰接，超静定刚架(图1)便可转化为铰化(图3)。

图1和图3所表示出的两个结构的弯矩图和剪力图是完全相同的。

如果把弯矩为零的截面位置作为已知截面位置，求解图3所示铰化结构的内力，便可得到图1所示超静定刚架的内力。

根据同样的道理求得了单跨两层, 刚架受水平均布荷载作用、单层1～5跨刚架受竖向均布荷载作用时弯矩为零的截面位置系数a值，列入表1、2。

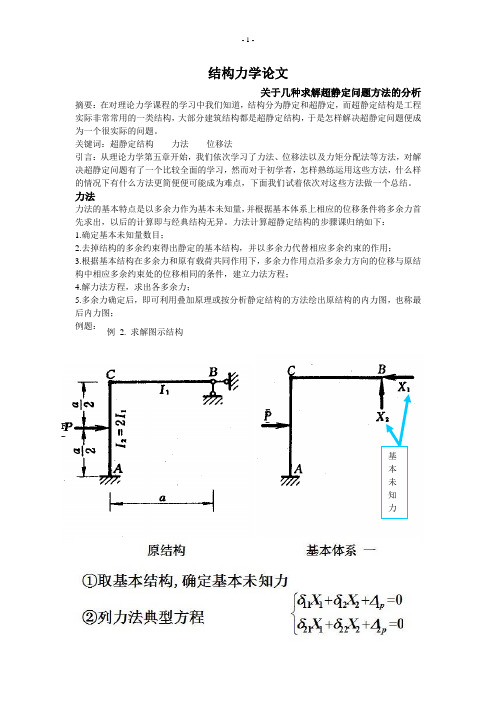
结构力学论文关于几种求解超静定问题方法的分析摘要：在对理论力学课程的学习中我们知道，结构分为静定和超静定，而超静定结构是工程实际非常常用的一类结构，大部分建筑结构都是超静定结构，于是怎样解决超静定问题便成为一个很实际的问题。

关键词：超静定结构力法位移法引言：从理论力学第五章开始，我们依次学习了力法、位移法以及力矩分配法等方法，对解决超静定问题有了一个比较全面的学习，然而对于初学者，怎样熟练运用这些方法，什么样的情况下有什么方法更简便便可能成为难点，下面我们试着依次对这些方法做一个总结。

力法力法的基本特点是以多余力作为基本未知量，并根据基本体系上相应的位移条件将多余力首先求出，以后的计算即与经典结构无异。

力法计算超静定结构的步骤课归纳如下：1.确定基本未知量数目；2.去掉结构的多余约束得出静定的基本结构，并以多余力代替相应多余约束的作用；3.根据基本结构在多余力和原有载荷共同作用下，多余力作用点沿多余力方向的位移与原结构中相应多余约束处的位移相同的条件，建立力法方程；4.解力法方程，求出各多余力；5.多余力确定后，即可利用叠加原理或按分析静定结构的方法绘出原结构的内力图，也称最后内力图；例题：F PFP例2. 求解图示结构基本未知力位移法由于在一定的外因作用下，结构的内力和位移之间恒具有一定的关系，于是可把结构的某些位移作为基本未知量，首先求出它们，然后再据此确定结构的内力，这样的方法称为位移法。

位移的计算的步骤归纳如下;1.确定位移法基本未知量，加入附加约束，取位移法基本体系；2.令附加约束发生与原结构相同的节点位移，根据基本结构在载荷等外因和节点位移共同作用下产生的附加约束的总反力（矩）=0，列位移法典型方程；3.绘出单位弯矩图、载荷弯矩图，利用平衡条件求系数和自由项；4.解方程，求出节点位移；5.用公式叠加最后弯矩图，并校核平衡条件；6.根据M 图由杆件平衡求Q ，绘Q 图，再根据Q 图由节点投影平衡求N ，绘N 图；力矩分配法力矩分配法采用轮流放松各节点的方法，使所有刚结点逐步达到平衡，属于渐进法。

第八章力法本章主要内容1）超静定结构的超静定次数2）力法的解题思路和力法典型方程（显然力法方程中所有的系数和自由项都是指静定基本结构的位移，可以由上一章的求位移方法求出（图乘或积分））3）力法的解题步骤以及用于求解超静定梁刚架桁架组合结构（排架）4）力法的对称性利用问题，对称结构的有关概念四点结论5）超静定结构的位移计算和最后内力图的校核6）§8-1超静定结构概述一、静力解答特征：静定结构：由平衡条件求出支反力及内力；超静定结构的静力特征是具有多余力，仅由静力平衡条件无法求出它的全部（有时部分可求）反力及内力，须借助位移条件（补充方程，解答的唯一性定理）。

二、几何组成特征：（结合例题说明）静定结构：无多余联系的几何不变体超静定结构：去掉其某一个或某几个联系（内或外），仍然可以是一个几何不变体系，如桁架。

即：超静定结构的组成特征是其具有多余联系，多余联系可以是外部的，也可能是内部的，去掉后不改变几何不变性。

多余联系（约束）：并不是没有用的，在结构作用或调整结构的内力、位移时需要的，减小弯矩及位移，便于应力分布均匀。

多余求知力：多余联系中产生的力称为三、超静定结构的类型（五种）超静定梁、超静定刚刚架、超静定桁架、超静定拱、超静定组合结构四、超静定结构的解法综合考虑三个方面的条件：1、平衡条件：即结构的整体及任何一部分的受力状态都应满足平衡方程；2、几何条件：也称变形条件、位移条件、协调条件、相容条件等。

即结构的变形必须符合支承约束条件（边界条件）和各部分之间的变形连续条件。

3、物理条件：即变形或位移与内力之间的物理关系。

精确方法：力法（柔度法）：以多余未知力为基本未知量位移法（刚度法）：以位移为基本未知量。

力法与位移法的联合应用：力法与位移法的混合使用：混合法近似方法：力矩分配法、矩阵位移法、分层总和法、D值法、反弯点法等本章主要讲力法。

五、力法的解题思路（结合例子）把不会算的超静定结构通过会算的基本结构来计算。