当前位置：文档之家 › 静定刚架内力计算

静定刚架内力计算

  • 格式：ppt
  • 大小：964.00 KB
  • 文档页数：45

下载文档原格式

  / 45

合集下载

03结构力学 第三章 静定结构的内力计算3.3 静定刚架的内力计算(邓军)

03结构力学 第三章 静定结构的内力计算3.3 静定刚架的内力计算(邓军)
剪力图： 剪力符号规定与直梁中的规定相同；剪力图可画在杆件的任一 侧，但剪力图上要标明正负号。 轴力图：
轴力仍以受拉为正，受压为负；轴力图可画在杆件的任一侧或 与纵坐标对称地画在杆件的两边，但需在轴力图上标明正负号。
§3.3 静定刚架的计算
例1 绘制如图所示门式刚架在半跨均布荷载作用下的内力图。
§3.3 静定刚架的计算
§3.3 静定刚架的计算
§3.3 静定刚架的计算
§3.3 静定刚架的计算
静定刚架的组成及类型
平面刚架是由直杆（梁和柱）组成的平面结构。
刚架中的结点部分或全部是刚节点。
在刚节点处，各杆件连成一个整体，杆件之间不能发生相对 移动和相对转动，刚架变形时各杆之间的夹角保持不变，因 此刚节点能够承受弯矩、剪力和轴力。
解：
1）求支座反力 由整体平衡方程可得
M A 0, 6 3 12FyB 0 M B 0, 6 9 12FyA 0
X 0, FxA FxB 0
取铰C右边部分为隔离体
MC 0, 6.5FxB 6FyB 0
求得
FyB =1.5kN() FyA=4.5kN() FxA =1.384 kN()
§3.3 静定刚架的计算
2）作弯矩图
求出杆端弯矩（设弯矩方正向为使刚架内侧受拉）后，画于受 拉一侧并连以直线，再叠加简支梁的弯矩图。
以DC杆为例
M DC 1.384 4.5 6.23kN m, MCD 0
CD中点弯矩为 1.3845.5 133 1 1 4.5 6 1.388kN m 22
（2）为计算静定刚架位移和分析超静定刚架打下基础。
2）刚架各杆内力的求法
从力学观点看，刚架是梁的组合结构，因此刚架的内力求法 原则上与梁的内力计算相同。 通常是利用刚架的整体或个体的平衡条件求出各支座反力和 铰接点处的约束反力，然后用截面法逐个计算杆件内力。

第三章 静定结构的内力计算

第三章 静定结构的内力计算

FAy
1 3a 4 FP a M q 3a 3a 2 5
第三章
静定结构的内力计算
M
B
0
3a 4 FAy 3a M q 3a FP a 0 2 5 1 3a 4 FAy FP a M q 3a 3a 2 5
第三章
无荷载 平行轴线
Q图
静定结构的内力计算
均布荷载
集中力 发生突变
P
集中力偶
无变化 发生突变
m
斜直线
M图
二次抛物线 凸向即q指向
出现尖点
两直线平行 备 注
Q=0区段M图 Q=0处，M 平行于轴线 达到极值
集中力作用截 集中力偶作用 面剪力无定义 面弯矩无定义
在自由端、铰支座、铰结点处，无集中力偶作用，截面弯矩 等于零，有集中力偶作用，截面弯矩等于集中力偶的值。
第三章 静定结构的内力计算
第三章
静定结构的内力计算
§3-1单跨静定梁
一、静定结构概述 1．概念：是没有多余约束的几何不变体系。 2．特点：在任意荷载作用下，所有约束反力和内力都 可由静力平衡方程唯一确定。 平衡方程数目 = 未知量数目 3．常见的静定结构 常见的静定结构有：单跨静定梁、多跨静定梁、静 定平面刚架、三铰拱、静定平面桁架、静定组合结构等 (如下图）。
0 FYA FYA 0 FYB FYB
A
x
C
L
斜梁的反力与相应简支 梁的反力相同。
第三章
（2）内力
静定结构的内力计算
求斜梁的任意截面C的内力，取隔离体AC： a FP1 A
FYA x Fp1 FYA
0
MC

结构力学二3-静定结构的内力计算

结构力学二3-静定结构的内力计算

以例说明如下
例 绘制刚架的弯矩图。 解：
E 5kN
由刚架整体平衡条件 ∑X=0 得 HB=5kN← 此时不需再求竖向反力便可 绘出弯矩图。 有：
30
20 20 75 45
40
0
MA=0 , MEC=0 MCE=20kN· m（外） MCD=20kN· m（外） MB=0 MDB=30kN· m（外） MDC=40kN· m（外）
有突变
铰或 作用处 自由端 (无m）
m
Q图
M图
水平线
⊕
⊖㊀
Q=0 处 突变值为P 如变号 无变化
有极值 尖角指向同P 有极值 有突变 M=0 有尖角
斜直线
→
↑
利用上述关系可迅速正确地绘制梁的内力图（简易法）
简易法绘制内力图的一般步骤：
（1）求支反力。 （2）分段：凡外力不连续处均应作为分段点， 如集中力和集中力偶作用处，均布荷载两端点等。 （3）定点：据各梁段的内力图形状，选定控制 截面。如集中力和集中力偶作用点两侧的截面、均 布荷载起迄点等。用截面法求出这些截面的内力值， 按比例绘出相应的内力竖标，便定出了内力图的各 控制点。
说明：
（a）M图画在杆件受拉的一侧。 （b）Q、N的正负号规定同梁。Q、N图可画在杆的 任意一侧，但必须注明正负号。 （c）汇交于一点的各杆端截 面的内力用两个下标表示，例如： MAB表示AB杆A端的弯矩。 MAB
例 作图示刚架的内力图
RB↑
←HA
VA→
CB杆：
由∑ X=0 可得： M = CD RB=42kN↑ HA=48kN←， H （左） A=6×8=48kN← 由∑M144 VA=22kN↓ 48 A=0 可得： MEB=MEC=42×3 ↑ （2）逐杆绘M图 R=126kN = 126 · m （下） B 192 MDC=0 CD杆： M =42 × 6-20 × 3 由 ∑Y=0 可得： CB MCD=48kN·m（左） =192kN· m（下） VA=42-20=22kN↓

结构力学刚架

结构力学刚架

qa
返回
三、 三铰刚架弯矩图
1 反力计算 ↓↓↓↓↓↓↓↓↓↓↓↓↓↓ 0 1 整体 C MA= qa2+2qa2－2aYB=0 (1) 2 右半边 2 qa MC=0.5qa2+2aXB 1/2qa －aYB=0 (2) 解方程(1).(2)可得 A XB=0.5qa YB=1.5qa qa/2 XA 3 再由整体平衡 a a A X=0 解得 XA=－0.5qa Y Y=0 解得 YA=0.5qa 2 绘制弯矩图 a a
结构力学
静定刚架
4.3.3 计算实例
• • • • • 1） 2） 3） 4） 5） 悬臂刚架 简支刚架 三铰刚架 多跨静定刚架 对称性的利用
如静定刚架仅绘制其弯矩图，往往并不需要求出全部反 力，只需求出与杆轴线垂直的反力。 一、悬臂刚架绘制弯矩图可以不求反力，由自由端开始作 内力图。 q ql² ↓ ↓↓↓↓↓↓↓↓ ½ql² 2q 2q
系，可在绘制内力图时减少错误，提高效率。
另外，根据这些关系，常可不经计算直观检查 M 图的轮廓是否正确。
①M 图与荷载情况不符。 ②M 图与结点性质、约束情况不符。 ③作用在结点上的各杆端弯矩及结点集中力偶不满 足平衡条件。
qa
a
a qa2
a
2a
a
a
a
qa
A
B H
C
q
↓↓↓↓↓↓↓↓↓↓↓
qa2/2 F D
qa
qa2/2
G
E
qa2
qa2/2 M图（kN.m）
绘制图示刚 架的弯矩图 仅绘M图,并不需要 求出全部反力. 先由AD ∑Y=0 得 YA=80kN 再由整体 ∑X=0 得 XB=20kN 然后先由A.B支座开始 作弯矩图.

工程力学31 静定平面刚架的内力计算

工程力学31 静定平面刚架的内力计算
35
F
C
XE E
B
YE
YE
A
XE
33
FP
FP a
D
F
2FPa 2FP 0
A
E0
FP 2FP
FP
C
D
F
FP
B
0 XE E
FP
2FP YE
FP
2FP
34
C
B
FRB FP FP
变形曲线
结构的变形曲线：
1. 必须符合支座的约束条件和杆件的联结条件； 2. 必须正确反映结点线位移和角位移的方向； 3. 必须正确反映杆件的弯曲方向。
静定平面刚架的内力
1
31
❖ 由多根直杆组成 ❖ 杆件之间的结点多为刚结点
2
刚结点
❖变形特点：限制相对的转动和移动 ❖受力特点：可传递弯矩、剪力和轴力
3
32
悬臂刚架 简支刚架
三铰刚架
4
3 ❖内力类型：弯矩、剪力、轴力 ❖计算方法：截面法 ❖内力的符号规定：
弯矩：取消正负规定，弯矩图画在受拉一侧。 剪力：符号规定不变。 轴力：符号规定不变。 轴力图和剪力图习惯上同号画在同侧，标明正负
（2） 作M图
10
（3） 作FQ图
由隔离体平衡条件求杆端剪力
FQAD 1.384kN
FQBE 1.384kN
FQDC
1 6.23 6 3 3.83kN
6.23
FQCD
1 6.23
6.23
6 3
1.86kN
FQCE
1 6.23
6.23
0.985kN
11
1.384 4.5
1.384
（4） 作FN图 由结点平衡条件求杆端轴力

静定梁与静定刚架

静定梁与静定刚架

（二）绘内力图：
H A
=0
V
A =130KN
X 0 Y 0 M 0
C
NC 0 QC 130 KN M C 130 KN .M
第3章 例题: 试绘制图示外伸梁的内力图。
解：
10KN/m A HA=0 4m C 2m D B E 30KN.m 20KN
（1）计算支座反力
2m
2kN E
2m F
F
2m
G 2kN
2m
（b）
A
4kN/m B
C
G 2kN
G
B
11kN 4
4kN
4
（d）
8 7
（e） 9
4 M（kN.m） 2 2
Q（kN）
2
第3章 例题2： 图示三跨静定梁，全长承受均布荷载q，试确定铰E、F的位置，使中 间一跨支座的负弯矩与跨中正弯矩数据数值相等。
第3章
3.3 静定平面刚架的内力计算 一、刚架的组成 1、刚架的特征 由若干梁和柱用刚结点联结而成的结构。具有刚结点是 刚架的主要特征。 2、刚架的应用 刚架在工程上有广泛的应用。
（1）斜梁的倾角为常数，而曲梁各截面的的倾角是变量。 （2）计算曲梁的倾角时，可先写出曲梁的轴线方程y=f(x),而后对x求一 阶导数，进而确定倾角：
dy tan ; dx
tan1 (tan )
（3）角以由x轴的正方向逆时针转到切线方向时为正，反时针方向为负。
例题：试求图示曲梁C截面的内力值。已知曲梁轴线方程为：
y 4f 4 4 (l x) x 2 (12 1.5) 1.5 1.75m l2 12
4f 4 4 tan yx 1.5 2 (l 2 x) x1.5 2 (12 2 1.5) 1 l 12 2 450 sin con 0.707 2

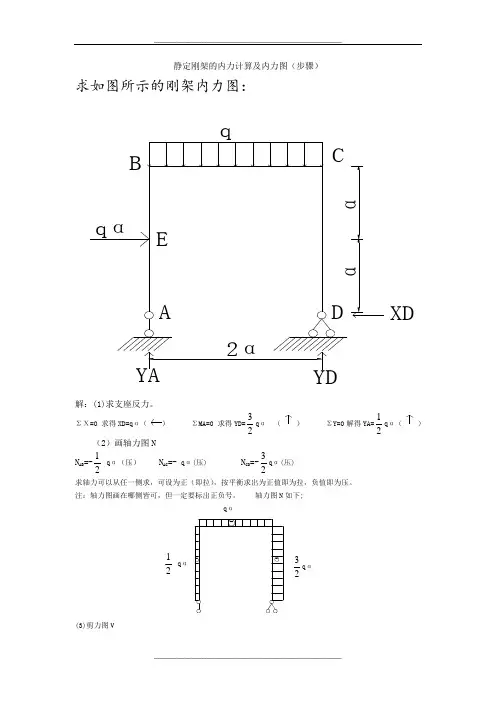
静定刚架的内力计算及内力图

静定刚架的内力计算及内力图

静定刚架的内力计算及内力图（步骤）求如图所示的刚架内力图：qXD解：(1)求支座反力。

ΣΧ=0 求得XD=q α（） ΣMA=0 求得YD=32q α （） ΣY=0解得YA=12q α（）（2）画轴力图N N AB =-12 q α（压） N AC =- q α(压) N CD =-32q α(压) 求轴力可以从任一侧求，可设为正（即拉），按平衡求出为正值即为拉，负值即为压。

注：轴力图画在哪侧皆可，但一定要标出正负号。

轴力图N 如下;q α32q α(3)剪力图VV AE =0 V EB =- q α V DC =q α V BC =12q α V CB =-32q α v cd=q α 特点：没有荷载部分为平直线，有均布荷载部分为斜直线。

剪力图V 如下剪力图画在哪侧皆可，（4）画弯矩图（刚架内侧受拉为正，外侧受拉为负）区段叠加的控制点为 1 端部 2均布荷载的起止点 3其他的位置可分开求或叠加（一般在一个段内有集中力作用在均布荷载的位置上时，在集中力处分开。

） 先求每根杆两端的弯矩，用虚线连接，段间空载的直接连接，有力的叠加。

M 图特点：1均布荷载：抛物线 2无荷载：直线 3集中力:与力一致的方向产生尖点叠加大小 集中力点处：力的方向叠加Fab l（特别地，当α=b 时代入式子为fl 41） 均布荷载中点：28qlM AB =0 M BA =q α2(左) M DC =0 M CD = q α×2α=2q α2(右)M BC = q α2(上) M CBCD受力处E l22a 0，再用直线连接即可。

注：不管是简支梁与否，受力处的叠加都是加上M=Fabl。

受均布荷载的中点处叠加的弯矩的大小是向力的方向移动M=28ql 注：此处所说的简支是两端有支撑即可。

静定梁和刚架内力分析

静定梁和刚架内力分析

(0＜x＜l ) (0≤x＜l)
M
(-)
(c)
x
2.作剪力图和弯矩图：
由剪力方程可知，当 0 <x <l，时（即 AB 段上），剪力为 常数，因此剪力图为一条水平的直线；由弯矩方程可知，AB 梁段上沿着轴线方向弯矩呈线性变化，因此，弯矩图为一条斜 直线，只需求出两个端截面上
F A FQ x m m l
在列平衡方程求解内力时，需事先确定截面内力的方向， 而此时截面内力为未知力，因此，一般假定截面内力沿其正向 作用，则计算得到的正负号就是该截面内力的正负号。 另外，在利用截面法求解前，通常先确定支座反力，因支 座反力并无正负规定，在求支反力前可任意假设正方向。
若结果为正，则表示支反力实际方向与假设方向相同；
上所有外力对该截面形心的力矩的代数和。
其中外力对横截面形心之矩正负号选取规律为： （1）力——不论横截面左侧还是右侧，只要向上就取正，
反之取负；
（2）力偶——横截面左侧顺时针或右侧逆时针取正，反之 取负。 利用上述结论，可以不画分离体的受力图、不列平衡方 程，直接得出横截面的剪力和弯矩。这种方法称为直接法。 直接法将在以后求指定截面内力中被广泛使用。
2
求梁指定截面上的内力的方法： 剪力：梁任一横截面上的剪力在数值上等于该截面一侧梁段 上所有外力在平行于截面方向投影的代数和。 其中外力正负号选取规律为： 横截面左侧梁段上向上的外力取正，横截面右侧梁段上
向下的外力取正；反之取负。
简记为左上右下取正，反之取负。
弯矩：梁任一横截面上的弯矩在数值上等于该截面一侧梁段
若外力或外力偶矩使所考虑的梁段产生向下凸的变形(即 上部受压，下部受拉)时，等式右方取正号，反之，取负号。 此规律可简化记为“下凸弯矩正”或“左顺，右逆弯矩 正” ，相反为负。

6-2-2静定平面刚架的内力计算和内力图绘制.

6-2-2静定平面刚架的内力计算和内力图绘制.

（1）刚架任一横截面上的弯矩，其数值等于该截面任一边刚架
上所有外力对该截面形心之矩的代数和。力矩与该截面上规定的 正号弯矩的转向相反时为正，相同时为负。 （2）刚架任一横截面上的剪力，其数值等于该截面任一边刚架上 所有外力在该截面方向上投影的代数和。外力与该截面上正号剪 力的方向相反时为正，相同时为负。
作用点、分布荷载作用的起点和终点等）和杆件的连接点作为控
制截面，按刚架内力计算规律，计算各控制截面上的内力值。
国家共享型教学资源库
四川建筑职业技术学院
（3）按单跨静定梁的内力图的绘制方法，逐杆绘制内力图， 即用区段叠加法绘制弯矩图，由微分关系法绘制剪力图和轴 力图；最后将各杆的内力图连在一起，即得整个刚架的内力 图。
M BE 0
M EB FBx 4.5 62.1 kN m （右侧受拉）
M CE 0
M EC M EB 62.1 kN m
（上侧受拉）
四川建筑职业技术学院
国家共享型教学资源库
（3）绘剪力图。
FS AD FS DA 13.8 kN
FS BE FS EB 13.8 kN
四川建筑职业技术学院
例6－3 绘制图所示简支刚架的内力图。
解 （1）求支座反力。 FAx=16 kN, FBx=12 kN, FBy=24 kN
国。将刚架分为AC、CE、CD和DB
四段，取每段杆的两端为控制截面。这些截面上的内力为
MAC=0 MCA=－2kN/m×6m×3m=－36kN· m （左侧受拉） MCD= MCA=－36 kN· m （上侧受拉） MDC=－12kN×6m +12 kN· m =－60 kN· m （上侧受拉） MDB=－12kN×6m =－72 kN· m （右侧受拉） MBD=0 FSAC=0 FSCA=－2kN/m×6m=－12 kN FSCE= FSEC=16kN FSED=FSDE=－24kN FSDB=FSBD=12kN FNAC=FNCA=－16kN FNCD=FNDC=－12kN FNDB=FNBD=－24kN

工程力学中静定结构的内力计算

工程力学中静定结构的内力计算

a
a
B XB X
YB
∑X=0 XC=XB=25kN ∑Y=0 YC=60-55=5kN ∑X=0 XA=25-40= -15kN
a
5kN

25kN
C

2m
y
25kN Fs 图

C
60kN

55kN
A
20kN· m
15k B N A 5kN
4m
25kN
B 4m
C
25kN 55kN
X
C
P2 P1 k y H A VA a3 b3 B VB H x 三铰拱与相应之简 支梁反力比较： VA =VA ° P3 B VB ° VB =VB ° HA=HB=H= MC°/f k C
P3
a2
a1 b1
b2
H=0
A VA°
P1
k1
P2 C
t
Mk
P1
y
n
k
Nk
∑Mk(F)=0， MK=[VAxk - P1 (xk- a1 )]-Hyk
FVb ×16 – 20 × 4 – 5 ×8 ×12=0
FVa=25KN FVb=35KN FHa=FHb
ΣMc=0
P=20Kn
FHa×4+20 ×4 – 25 ×8=0
FHc
FVc
FHa=30KN
FHa
4m 4m
FVa=25KN
4m
Σ Mo=0 . Mad=0 ΣХ=0. FQad+30=0
桁架的名称
上弦杆
桁高
斜杆 竖杆 下弦杆 跨度
1、按桁架的外形分为：
桁架的分类
a、三角形桁架
b、矩形桁架

《结构力学》静定结构内力计算

《结构力学》静定结构内力计算

只承受竖向荷载和弯矩
FP1 A
FP2
B
C
基本部分：能独立承受外载。 附属部分：不能独立承受外载。
FP
A
B
C
■作用在两部分交接处的集 中力，由基本部分来承担。
FP1
FP2
A B
■基本部分上的荷载不影响附 属部分受力。
■附属部分上的荷载影响基本 部分受力。
先算附属部分， 后算基本部分。
例 确定x值，使支座B处弯矩与AB跨中弯矩相等，画弯矩图
ql ql/2
FQ图 ql
7ql/4 ql
5ql/4 ql/2
3ql/4
ql/2
练习
10kNm 20kN 10kN
10kN/m
1m 1m 1m 1m
1m 1m 10kN/m
10kNm
20kN 10kN 0
0
30kN
10kNm
20kN 10kNm
10kNm
10kNm
20kN 10kN 0
0
30kN
2m 2m
解 （1）求支反力
q=20kN/m FP=40kN
70kN
50kN
（2）取隔离体，求截面内力
MC C FQC
FP=40kN
B 50kN
（2）叠加法作弯矩图
120kNm
+
40kNm
40kNm
=
120kNm
40kNm
40kNm M图
例 试绘制梁的弯矩图。
40kNm
FP=40kN q=20kN/m
26
26
8 FQ图(kN)
6
12
M图(kNm)
24 12
例
解 （1）求支反力

静定结构的内力分析

静定结构的内力分析

40
第 三 章80 静定结构的内力计算
D
FNDE FNED
E
30
30
FNDC
FNEB
FQ
40 kN
FN 30 kN
80 kN
练习：
第三章
静定结构的内力计算
解： (1) 求支座反力。
F=qa
C
D
由 X 0
E
FxA q 2a 0
q
a B
得 FAx 2qa
a
由 M A 0
FxA
A
FyB
2qa a F a FyB 2a 0
首先进行定性分析。
由内力图的外观校核。杆上无分布荷载FS图为水 平直线；M图为斜直线。杆上有分布荷载FS图为斜直 线；M图为二次抛物线。 FS图为零的截面M为极值。 杆上集中荷载作用的截面, FS图上有突变；M图上有折 弯。根据这些特征来检查，本题的M图、FS图均无误。
第 三 章 静定结构的内力计算
6
FA=58 kN 26
10
18 FB=12 kN
q ME
FQE
MF
FS 图 ( kN )
FQF
第 三 章 静定结构的内力计算
二、 多跨静定梁 (multi-span statically determinate beam)
附属部分--依赖基本
基本部分--不依赖其它
部分的存在才维持几
部分而能独立地维持其
据
3.外力与杆轴关系(平行,垂直,重合) 4.特殊部分(悬臂部分,简支部分)
5.区段叠加法作弯矩图
第 三 章 静定结构的内力计算
结点平衡条件的应用：
一、铰结点： （集中力偶只能作用于杆端处）
M

刚架的内力计算

刚架的内力计算
j — 该截面所属杆件的另一端。
例如：
MAB表示AB杆A端的弯矩。 MAC表示AC杆A端的弯矩。
A
MAC
MAB
求内力的方法： 截面法
2
作静定平面刚架内力图的步骤
（1）求支座处的约束力；
（2）计算各杆杆端弯矩、杆端剪力、杆端轴力， 逐杆画出弯矩图、剪力图、轴力图。 — 弯矩图画在受拉边，图上不标正、负号； — 剪力图和轴力图可绘在杆件的任一侧，但要 标上正、负号，正、负号规定与梁一致。 （3）校核。可取刚结点或刚架中任意部分为研究 对象，验算是否满足平衡条件。
3
例 题 1-1
试画出刚架的内力图。
B' B" C
q l 2
B
MBC
ql 2
=ql2/2
FSBC＝－ql/2
FNBC=0 FSCB＝－ql/2 FNBA= ql/2 FNCB=0 MCB=0
BFSBA=0
A q l 2 ql
ql
ql
2
MBA=ql2/2
B'
FNAB= ql/2 MAB=0
ql
A
FSAB=ql
3ql / 8
l/2 l/2
2
l
D
3ql2/8
3ql2/8
3ql / 2
平衡！
6
例 题3
试分析刚架的AB、BC段是受何种组合变形。
F y
a Mx=2Fa x Mz =2Fa A Mx=2Fa B F Mx= TBA=2Fa
Mz =Fa
A
B
MAB=2Fa
F
z
m
C
TAB=2Fa
ABBC
m
MBC=2Fa TBC= -Fa

《结构力学》第三章 静定结构内力计算(1)

《结构力学》第三章 静定结构内力计算(1)

技巧：“求谁不管谁”：不考虑待求未知力，而考虑其
它未知力有什么特点，具体分为下面两种情况：
（a）其余未知力平行，在其垂直方向投影。
（b）其余未知力汇交于一点，对该点取矩。
X 0,X A 0;
1
1
MB
0,YA
l ql
l 2
0,YA
ql 2
Y
0,YA
YB
ql
0,YB
1 2
ql
step2：求指定截面内力 （1）取脱离体：从指定c截面截开梁，取左半脱离体为 研究对象，受力如图所示：
轴力、剪力 符号规定
梁、拱的弯 矩符号通常 假定使下侧 受拉为正
2、杆件任一截面上内力的计算---截面法
沿计算截面用一假想截面将构件切开，任取一侧 脱离体为研究对象，利用脱离体的静力平衡条 件，可建立三个平衡方程：
X 0,Y 0,M 0
由此就可求得杆件任一截面上的内力。
注意：
• 脱离体要与周围的约束全部断开，并用相应的约束力 代替。例如，去掉辊轴支座、铰支座、固定支座时应 分别添加一个、二个以及三个支座反力，等等。
（二）简支结构
通过一铰、一链杆或三根链杆与基础相连的结构。
（三）三铰结构
若结构体系（不含基础）有两个刚片，其与基础 的连接满足三刚片法则，则称该体系为三铰结 构。
（四）组合结构
多次运用几何不变体系的简单组成规则构成的结 构。
2、静定结构内力分析（即绘制内力图） 方法
有三种常用的绘制内力图的方法。
（2）熟记几种常见单跨梁的弯矩图，如悬臂梁、简
支梁等。特别记住简支梁在均布荷载、集中力以及集 中力偶作用下的弯矩图。
（1）
（2） （3）
梁长均为L

静定刚架内力计算

静定刚架内力计算
－3
3m
3m 9kN
cos 2 5
lDC lEC 3.35m
－
0.45
－
5.82
－
N图（kN）
9
6D
ααQQC1CCN.CENC7DE9D↓C↓↓47α↓k.↓1N↓α6↓/m3.58 E
1.79 3.13QDC2
Q 2
EC
NC 9E
校∑Q核NX∑Q∑QNXMCCNMMECEDEDCE=XC(D=CE==N1C3=2=6.C07－3－66+EYN.9.－+4+N55Q(7D5333k83.kC.C(.E.8N131.31kN×DCc532.)63N×o18×=)kkks23cQ4N3NN+1o×.D4.0s3+7C5.5149×1＝.×+57.()51973s02+..si.5n51i3n8+6.+03+315(+..1731Q2.975)E9QsC50in＝C3E.5＝008)00cos
绘制图示刚 架的弯矩图
仅绘M图,并不需要 求出全部反力.
先由AD ∑Y=0
得 YA=80kN
A ↓↓↓↓↓↓↓↓↓↓
D 120
E q=20kN/m
80kN 90
120 ↓↓↓↓↓↓↓↓
F
C
180 MEA=80×6-½ ×2200×k6N²=120
60
120
62.5
180
再由整体
∑X=0 得 XB=20kN
状特征和绘制内力图的叠加法。
4.会恰当选取分离体和平衡方程计算静定结构的内力。如何选取视具体情况（结构情 况、荷载情况）而定。当不知如何下手时，宜考察结构的几何组成。

静定结构的内力计算—静定平面刚架的内力计算(工程力学课件)

静定结构的内力计算—静定平面刚架的内力计算(工程力学课件)
变体系的组成规则连接附属部分。
简支刚架
悬臂刚架
三铰刚架
三、静定平面刚架内力分析步骤
方法:
➢ 求支座反力 ➢ 拆成单个直杆,求出每个杆两端的内力
及各控制截面的内力 ➢ 按与单跨梁相同的方法画内力图.
求反力，分段，定点，连线
关于分段：
E D
（1）分成AC、CB两段 （2）AC分成AD、DC两段
CB分成CE、EB两段
【例 4】画刚架的弯矩图 注意画图时的分段！
只有两杆汇交的刚结点，若结点上无外力偶作 用，则两杆端弯矩必大小相等，且同侧受拉。
【例 5】画刚架的弯矩图
A
C B
D
三根杆连接的刚结点 处有力偶！
E
刚节点 力矩平衡
静定平面刚架的内力计算
一、平面刚架的特点
由梁和柱组成，梁和柱用刚结点相连接。
1 8
ql2
l
1 ql2 8
梁
刚架
弯矩分布均匀 可利用空间大
刚结点特征：
受力特征——刚结点能承 受并能传递弯矩，内力分 布均匀。
变形特征——变形前后各杆 端之间的夹角保持不变。
1 ql2 8
A A α
α
几何特三个约束，依靠刚结点可用
较少的杆件便能保持其几何不
变性；具有较大的净空。
二、静定平面刚架分类
（1）简支刚架——用三根链杆或一个铰和一根链杆与基础 相连组成的刚架；
（2）悬臂刚架——用固定端与地基相连，如车站站台； （3）三铰刚架——三个刚片(包括基础)用三个铰两两相连。 （4）组合刚架——主从刚架。在上述基本部分上，据几何不
【例1】画图示简支刚架的弯矩图 MCB=24 MBC=0
MCA=24 MAC=0

结构力学第4章静定刚架的内力计算

结构力学第4章静定刚架的内力计算

GDCB部分： 见图(c)右。计算如下：
FX 0
FCx 1kN (←)
MC 0
FBy

1 (q 6 3 8 6 1 4 4
FP
2)

30kN(↑)
MB 0
FCy

1 4
(q

4

2

q

2
1

8

2

1
4

FP
2) 2kN(↑)
2）作内力图：
结构力学
结构力学教研室
青岛理工大学工程管理系
第四章
静定刚架的内力分析
§4.1 概 述
组成刚架的杆件主要产生弯曲变形， 可承受弯矩。
刚架的构造特点: 具有刚结点
(a)
(b)
(c)
刚结点的特点:
能传递力矩 （弯矩）
静定刚架有如下几种最简形式, 较复杂的刚架一般是由若干简 单刚架按基本组成规则构成的。
由 M A 0 得：
1 L L qL
FBy

q L
2

4

8
(↑)
(a)
由 M B 0 得：
FAy

1 q L
L (L 24

L) 2
3qL 8
(↑)
(b)
如取截面I-I以右部分，由 MC 0
得：
FBx

1 L
FBy

L 2

qL(←)
16
再由整体的平衡方程 FX 0
（右侧受拉）
结点C：
MCD
FNCD FQCD MCB
FQCB
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
↑↑↑↑↑↑↑↑ ↑↑↑↑↑↑↑↑ A
M图 a qa/2
QCA
q
NCB
QAC
0 NCA ∑X＝0，NCB ＝ 0 ∑Y＝0，NCA＝qa/2
∑MC＝qa2/2+ qa2/2 －QACa=0 QAC=（qa2/2+ qa2/2 ）/a =qa ∑MA＝0 Q CA=（qa2/2 － qa2/2 ）/a =0
例题 1
反力计算1
三铰刚架的反力计算
整体对右底铰建立矩方程 qa 2 0 Y qa =3kN M B 0 2aYA 2 A 4 左半边平衡 qa qa M C a X A ×1.5a 0 X A 2(kN ) 4 6 整体平衡 Y YA +YB qa 0 YB 3qa 4 9kN
O
qL2/ห้องสมุดไป่ตู้ q
C
qL2/4 整体对O点建立平衡方 程得 ∑MO=ql×1.5l－ 2lXA=0 得 XA=3ql/4 RB
l
A
=3/4ql XA
l l 三铰刚架弯矩图
B
YA
返回
四、主从结构绘制弯矩图时，可以利 用弯矩图与荷载、支承及连结之间的 对应关系，不求或只求部分约束力。 以铰支座、铰结点、自由端作为切入 点，先作附属部分，后作基本部分。
q=4kN/m a=3m
q ↓↓↓↓↓↓ 1.5a
B
XB
C
X 0
X A X B 2kN
A
2
M C YA a X A a +
反力校核
qa + X B a YB a 2 2 2×3 3×3 2×4.5 + + 2×4.5 9×3 2 0
XA
a
YA
a
YA
返回
双截面法
例题 4
内力计算1
QDA=8kN QDB=8kN QDC=－6kN NDC QDC NDA=0 NDB=6kN NDC=0 8kN MDC=8kN.m（左拉） MDB=16kN.m（右拉） MDC=24kN.m（下拉）
QDA MDA MDC 6kN
NDA
QDA=8kN NDB MDB D NDA=0 QDB QDB=8kN 6kN D 0 MDC=8kN.m（左拉） NDB=6kN 8kN.m B 8kN 8kN MDB=16kN.m（右拉）
D
0
返回
3、主从刚架求反力：
• 需要分析其几何组成顺序，确定基本部 分和附属部分。先计算附属部分，在计 算基本部分。
例题 3
反力计算3
由附属部分ACD 由整体
M
D
4 X A 2×2 4×2×1 0
X A 3kN
4kN/m
↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓
M 0 Y 0 Y
a
l
↓↓↓↓↓↓↓↓↓
B
qa2/2
qa2/8
注意:BC杆CD杆的 A 剪力等于零,弯矩图 于轴线平行
a
a
qa
返回
三、三铰刚架弯矩图，往往只须求 一水平反力,然后由支座作起。
例题 8 三铰刚架
三、三铰刚架弯矩图
1 反力计算 ↓↓↓↓↓↓↓↓↓↓↓↓↓↓ 0 1 整体 C 2+2qa2－2aY =0 (1) MA= qa B 2 右半边 qa 1/2qa2 MC=0.5qa2+2aXB －aYB=0 (2) 解方程(1).(2)可得 A XB=0.5qa YB=1.5qa qa/2 A X 3 再由整体平衡 a a YA X=0 解得 XA=－0.5qa Y=0 解得 YA=0.5qa 2 绘制弯矩图 a a
⑶作用在结点上的各杆端弯矩及结点集中力偶不满足平衡条件。 如图g所示刚架，若取结点C为分离体，将发现它不满足结点的力矩 平衡条件。另外AC段上A处只产生竖向反力，所以AC段只受轴力， 该段弯矩图等于零。正确的弯矩图如图2-4h所示。
§4.5刚架弯矩图绘制
• 如静定刚架仅绘制其弯矩图，往往并不 需要求出全 部反力，只需求出与杆轴线 垂直的反力。
q=4kN/m 6 D α C
↓↓↓↓↓↓
1.5m
1.79
＋
3.58
＋
6
4.5 E
3m
－
M图（kN.m） A
2kN
3kN
B
2kN
2
－
Q图（kN）7.16
＋
2
4kN/m ND 3m 3m C ↓↓↓↓↓↓↓ 9kN CNEC α 1.79 7.16 3.58 C α ααQCE Q CD 6D sin 1 cos 2 l DC l EC 3.35m E 5 5 1.79 Q EC NC 3.13Q 2 2 0.45 9 DC E － 3 3.13 ∑M N CE + 3 13 cos (3.58 +1.79) sin X (C=6+3 .×)4×1.5+3.35QEC＝0 0 QEC －7.16kN + 7.16 = + － NX 20NNkN 2 +1.79 sin +1 0 0 2 CE X .45 EC DC cos 5 ∑ME=6－ 3 × 4×3.35＝0 CE＝0 ×1.5+3.35Q 5 ∑MD Y (1313+ 5.82 校核 N = =6－Qk N 0.45) sin + (1.79 3.58) cos 3 3. CD QCEDC 5..82 kN N EC 3.58kN － QCD=1.79(kN)=QDC － 3 3.58 2 1.79× 0 9 N图（kN）
K
YG 30kN
2kN
K
A
XA 2m 2m
G
K XK
校核：
4m
YG
YK
M
E
2 2 + 2 2 4 X A 4 X K +YK 4 0
返回
2m
2kN
B
2kN
F
2m
X 0
X K 1kN
C
D
E
H
§4.3 刚架内力计算
• 计算步骤：
①求支座反力。简单刚架可由三个整体平衡方程求出支座反力，三 铰刚架及主从刚架等，一般要利用整体平衡和局部平衡求支座反力。 ②求控制截面的内力。控制截面一般选在支承点、结点、集中荷 载作用点、分布荷载不连续点。控制截面把刚架划分成受力简单的 区段。运用截面法或直接由截面一边的外力求出控制截面的内力值 。 ③根据每区段内的荷载情况，利用“零平斜弯”及叠加法作出弯 矩图。作刚架Q、N图有两种方法，一是通过求控制截面的内力作 出；另一种方法是首先作出M图；然后取杆件为分离体，建立矩平 衡方程，由杆端弯矩求杆端剪力；最后取结点为分离体，利用投影 平衡由杆端剪力求杆端轴力。当刚架构造较复杂（如有斜杆），计 算内力较麻烦事，采用第二种方法。 ④结点处有不同的杆端截面。各截面上的内力用该杆两端字母作 为下标来表示，并把该端字母列在前面。 ⑤注意结点的平衡条件。
例题 9 主从刚架
四、主从结构
qa
绘制弯矩图时，可以利用弯矩图 与荷载、支承及连结之间的对应关系， 不求或只求部分约束力。 q qa
l
6q
返回
2m
ql²
二、简支型刚架弯矩图，往往 只须求出一个与杆件垂直的反 力,然后由支座作起。
例题 7 简支刚架
二、简支型刚架弯矩图
简支型刚架绘制弯 矩图往往只须求出一个 于杆件垂直的反力,然后 由支座作起
↓↓↓↓↓↓↓↓↓↓↓↓
l/2
q
ql2/2 ql2/2
D
qa2/2
C
q l
l/2
q l
q
8kN 6kN －6kN 8kN 16kN.m
B 24kN.m
NDC=0 C MDC=24kN.m（下拉）
6kN
0
4m ∑X = 8－8 = 0 ∑Y = －6－（－6） = 0
校核：
6kN
∑M = 24－8 － 16 = 0
2m
1m
A 8kN =－6kN QDC
作内力图
8kN
1m
8 6
－ ＋
16 8 24

5
5
返回
§4.4 刚架弯矩图对误判别
• 利用前述内力图与荷载、支承和联结之 间的对应关系，可在绘制内力图时减少 错误，提高效率。另外，根据这些关系， 常可不经计算直观检查M图的轮廓是否 正确。鉴于静定平面刚架M图的重要性， 而初学者又常易搞错，故掌握M图正误 判别是很有益的。下面结合例子说明画 M图时容易出现的错误：
一、悬臂刚架绘制弯矩图，可以不求 反力，由自由端开始作内力图。
例题 6 悬臂刚架
如静定刚架仅绘制其弯矩图，往往并不需要求出全部反 力，只需求出与杆轴线垂直的反力。 一、悬臂刚架绘制弯矩图可以不求反力，由自由端开始作 内力图。 q ↓↓↓↓↓↓↓↓↓ ql² ½ql² 2q 2q
↓↓↓↓↓
l
q
2m
Q kN
2m
6kN 8kN 6kN M kN.m
4m
＋
6 N kN
返回
例题 5
内力计算2
作刚架Q、N图的另一种方法：首先作出M图；然后取杆件 为分离体，建立矩平衡方程，由杆端弯矩求杆端剪力；最后取 结点为分离体，利用投影平衡由杆端剪力求杆端轴力。 qa2/2 q qa2/2 C C B B 2/2 QCB QBC qa ∑MC＝qa2/2+ QBCa=0 qa2/8 QBC=QCB=－qa/2 qa2/2 a
第四章 静定刚架内力计算
• 学习内容
• 静定结构反力计算和截面内力计算； 绘制内力图的基本方法；利用微分关系 及结点平衡条件简化内力图的绘制；叠 加法绘制弯矩图；静定刚架的组成特点 和受力特点；刚架的内力计算和内力图； 斜杆刚架和复杂刚架的计算；利用对称 性简化刚架的计算。