二年级奥数-简单一笔画
- 格式:doc
- 大小:30.00 KB
- 文档页数:1
第一讲一笔画问题小朋友们,你们能把下面的图形一笔画出来吗?如果用笔在纸上连续不断又不重复,一笔画成某种图形,这种图形就叫一笔画。
那么是不是所有的图形都能一笔画成呢?这一讲我们就一起来学习一笔画的规律。
典型例题例【 1】下面这些图形,哪个能一笔画?哪个不能一笔画?( 1)(2)(3)(4)分析图(1)一笔画出,可以从图中任意一点开始画该图,画到同一点结束。
经过尝试后,可以发现图(2)不能一笔画出。
图(3)不是连通的,显然也不能一笔画出。
图(4)也可以一笔画出,且从任何一点出发都可以。
通过观察,我们可以发现一个几何图形中和一点相连通的线的条数不同。
由一点发出有偶数条线,那么这个点叫做偶点。
相应的,由一点出发有奇数条数,则这个点叫做奇点。
再看图( 1)、(4),其中每一点都是偶点,都可以一笔画,且可以从任意一点画起。
而图(2)有 4 个奇点, 2 个偶点,不能一笔画成。
这样我们发现,一个图形能否一笔画和这个图形奇点,偶点的个数有某种联系,到底存在什么样的关系呢,我们再看一个例题。
例【 2】下面各图能否一笔画成?(1)(2)(3)分析图(1)从任意一点出都可以一笔画成,因为它的每一个点都是与两条线相连的偶点。
关于图(2),经过反复试验,也可找到画法:由 A B C AD C。
图中 B、D 为偶点, A、C 为奇点,即图中有两个奇点,两个偶点。
要想一笔画,需从奇点出发,回到奇点。
经过尝试,图( 3)无法一笔画成,而图中有 4 个奇点, 5 个偶点。
解图( 1)、(2)可以一笔画。
这样我们可以发现能否一笔画和奇点、偶点的数目有着紧密的关系。
如果图形只有偶点,可以以任意一点为起点,一笔画出。
如果只有两个奇点,也可以一笔画出,但必须从奇点出发,由另一点结束。
如果图形的奇点个数超过两个,则图形不能一笔画出。
例【 3】下面的图形,哪些能一笔画出?哪些不能一笔画出?分析图( 1)有两个奇点,两个偶点,可以一笔画,须由 A 开始或由 B 开始到 B 结束或到 A 结束。

一笔画【知识要点】1.概念:一笔画是指笔不离开纸,而且每条线都只画一次不准重复而画成的图形。
2.分类:图中的点可分两大类:(1)双数点:从这点出发的线的数目是双数的,叫双数点。
(2)单数点:从这点出发的线的数目是单数的,叫单数点。
3.规律:一个图形能否一笔画成,关键在于图中单数点的多少。
(1)凡是图形中没有单数点的一定可以一笔画成。
(2)凡是图形中只有两个单数点,一定可以一笔画成,画时必须从一个单数点为起点,最后以另一单数点为终点。
(3)凡是图形中单数点的个数多于两个时,此图肯定是不能一笔画成。
【题目】1 判断下面图形中哪些点是单数点哪些点是双数点。
2 下列图形中各有几个单数点?能一笔画成吗?3 判断下面图形能不能一笔画成?如果能,应该怎样画?A4下面图形能不能一笔画成?这什么?5 如图是一个大型花池中小路的平面图,你能否不重复地一次走完所有的小路?进出口应设在什么地方?6 将下图加上最少的线改成一笔画的图形。
7.将下图去掉最少的线改成一笔画图形。
8.下图中的线段代表小路,请小朋友想一想,能够不重复地爬遍小路的甲蚂蚁还是乙蚂蚁?该怎么爬?9.为迎接2008年奥运会在北京召开,你能一笔画出奥运会的五环图案吗?10.下图是一个公园的平面图,应怎样走才能使游客走通每条路而不重复,设计一条最佳路线。
11 一个公园的平面图如下,请你设计好入口、出口,并给出一条浏览路线,要求走遍每一条路且不重复。
12.如图,是一个公园的平面图,请你设计好入口、出口,并给出一种游玩路线,要求走遍每一条路且不重复。
13.如图,是一个名画展厅的平面图,要使参观者不重复地走遍每一条画廊,问:出口、入口应设在哪里?14.黑色的鱼与白色的鱼所能游动的河道如下图所示。
黑色的鱼在A点位置,白色的鱼在B点位置。
哪条鱼能不重复地游遍所有的河道?15.能用一根铁丝弯成下面的图形吗?16.一个邮递员投递信件要走的街道如图,为节约时间,他想自己设计一条线路,可以不重复的走遍每一条街道,你能帮帮他吗?17.一只蚂蚁要想不重复的爬遍每一条线路,应从哪里出发,到哪里结束?18.你能用一笔画成4条线段把下图的9个点都连起来吗?19.下图能否一笔画成?如果能,应怎样画?20.如图,在一个六面体的顶点A和B处各有一只蜗牛,它们比赛看谁能不重复地爬遍每一棱线到达C点。
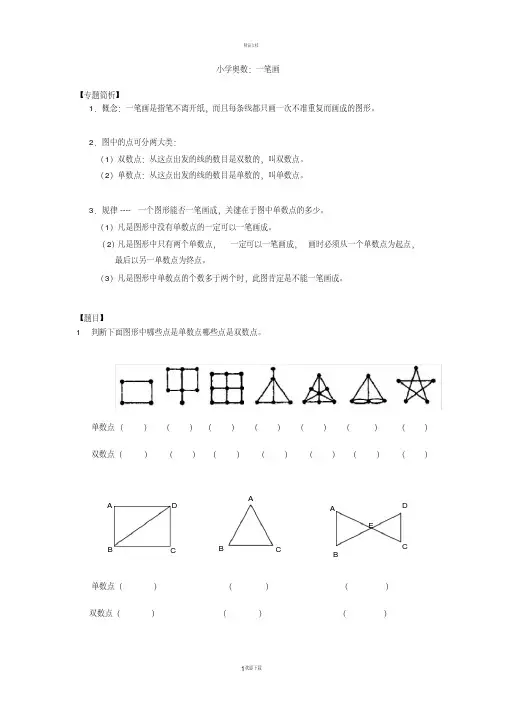

第八讲一笔画前续知识点:二年级第一讲;XX模块第X讲后续知识点:X年级第X讲;XX模块第X讲把里面的人物换成相应红字标明的人物.这里是小区平面图,我从哪个入口进去,才能一次不重复地走遍小区的所有小路,尽快地把口罩送给每个朋友呢?由于空气污染严重,哥哥让我给朋友们去送口罩,以防大家得病。
墨莫墨莫一笔画,是指从连通图的一点出发,笔不离纸,每条线都只画一次,不能重复.一笔画能解决很多实际问题.那么什么样的图形能够一笔画成,什么样的图形不能一笔画成呢?试着画一画下面的图形吧!例题1观察下列图形,能一笔画成的打“√”,不能一笔画成的打“×”.()()()()()()【提示】动手画一画,你知道什么样的图形一定不能一笔画成吗?练习1观察下列图形,能一笔画成的打“√”,不能一笔画成的打“×”.()()()()()()()()我们画了这么多图形,不难发现,不连通的图形一定不能一笔画成,能一笔画成的图形必定是连通图.连通图,指的是如果一个图形中的任意两点都是连通的,那么这个图形就是连通图.一个图形可以一笔画成,除了必须是连通图,还有没有其它的规律和特点呢?我们一起找找吧!首先,我们先来认识下面的两个名词:从一点出发的线条数目是奇数,如1、3、5、7、……我们称它为奇点. 从一点出发的线条数目是偶数,如2、4、6、8、……我们称它为偶点.奇点、偶点的个数与一个图形能否一笔画成有什么关系呢?我们来看一看下面的题目吧!【例题2】下面的各个图形都是由点和线组成的.请你仔细观察后回答,各图中的交叉点分别有几个奇点?几个偶点?能否一笔画成?能的在“( )”里打“√”,不能的在“( )”里打“×”.【提示】从某一点发出奇数条线,这个点是奇点;从某一点发出偶数条线,这个点是偶点.【练习2】下面的各个图形都是由点和线组成的.请你仔细观察后回答,各图中的交叉点分别有几个奇点?几个偶点?能否一笔画成?能的在“( )”里打“√”,不能的在“( )”里打“×”.(1) (2) (3)(4) 奇点数: ( ) ( ) ( ) ( ) 偶点数: ( ) ( ) ( ) ( ) 能否一笔画成:( ) ( ) ( ) ( )奇点数: ( ) ( ) ( ) ( ) 偶点数: ( ) ( ) ( ) ( )能否一笔画成:( ) ( ) ( ) ( )(1) (2)(3) (4)通过对上题的观察,相信大家都发现了规律.有0个奇点的连通图能够一笔画成.画时可以以任一点为起点,最后一定能以这个点为终点画完此图. 有2个奇点的连通图能够一笔画成.画时必须以一个奇点为起点,另一个奇点为终点画完此图. 有2个以上奇点的连通图不能一笔画成.根据以上规律,我们可以通过奇点个数来正确判断哪些图形能一笔画成,哪些图形不能一笔画成.我们就用学到的知识来解决生活中的一笔画问题吧!例题3草地上有许多小路,丁丁和月月分别站在A 、B 两个路口.谁能够一次不重复地走遍所有小路?【提示】谁的出发点是奇点?练习3花园里有许多崎岖的小路,小乖要浇花,它想一次不重复地走完每条小路.该从哪个路口出发呢?AB CDE例题4小河中有4个小岛,小岛之间建有六座桥.淘淘能一次不重复地走遍所有的小桥吗?【提示】先把实际地图画成“点线图”,然后数数奇点的个数吧!练习4蘑菇园的小朋友们要去游乐场玩,他们可以从6个入口进出游乐场.他们从哪个入口出发,才能一次不重复地走遍游乐场内的所有小路?我们已经可以正确判断哪些图形可以一笔画成,哪些不能一笔画成.如果不能一笔画成,可不可以通过增添或删除一些线的方法,让它变成可以一笔画成的图形呢?例题5AB C D EFG下面的“蝴蝶”能一笔画成吗?如果不能,按照如下要求把它改成能一笔画成的图形.(1)在图1中,去掉一条线;(2)在图2中,添加一条线.图1图2【提示】在两个奇点之间去掉或添加线.例题6甲乙两个不同公司的快递员去送货,两人都要以同样的速度走遍所有的街道(阴影部分),甲从A点出发,乙从B点出发,最后都回到C点.如果都选择最短的线路,谁先回到C点?ABC【提示】先把实际道路图画成“点线图”,再判断各个交叉点中有哪些是奇点.课堂内外七桥问题德国有一个城市叫哥尼斯堡.城中有一条小河,河中有两个小岛,还有7座桥把这两个小岛和陆地连接起来,如下图所示.人们经常在这里游玩,他们在游玩的时候提出这样一个问题:能不能一次不重复地走遍所有的小桥呢?作业1. 观察下列图形,能一笔画成的打“√”,不能一笔画成的打“×”.2. 下面每幅图中的交叉点分别有几个奇点?能否一笔画成呢?能的在“( )”里打“√”,不能的在“( )”里打“×”.( ) ( ) ( )( ) ( ) ( )小岛 小岛3. 菲菲周末去郊外的公园玩,公园里有许多崎岖的小路.她想不重复地一次走完每条小路,可以从哪个路口出发?4. 小熊、灰鼠、小象和小猪要分别从东、南、西、北四个入口去果园采果子,谁能不重复地一次走遍所有小路?5. 下面的图形能一笔画成吗?如果不能,按照如下要求将其改成能一笔画成的图形.(1)在图1中去掉一条线;(2)在图2中添加一条线.图1图2北CD E F G HBA 奇点数: ( ) ( ) ( ) ( ) 能否一笔画:( ) ( ) ( ) ( )(1) (2) (3) (4)第八讲 一笔画1.例题1答案:×,√,√,×,×,√详解:第(1)个图形是非连通图,不能一笔画;其它都是连通图,依次尝试判断即可. 2.例题2答案:如图所示:详解:把交叉点是奇点的圈起来,如图所示:有0个奇点和2个奇点的连通图能够一笔画成;2个奇点以上的连通图不能一笔画成.一个图形能否一笔画成与偶点数无关. 3.例题3 答案:月月详解:图中B 点和E 点是奇点,其它交叉点都是偶点.有2个奇点的图形,一笔画的特征是:从图形的一个奇点出发,回到另一个奇点.只有从奇点的路口出发,才能一次不重复地走遍所有小路.美羊羊站在B 点的路口上,所以能够一次不重复地走遍所有小路. 4.例题4 答案:不能详解:把图中的小岛看成点,把桥看成线,得到“点线图”,如图所示,有4个交叉点,这4个交叉点都是奇点,这个图形不能一笔画成.所以淘淘不能一次不重复地走遍所有的小桥.5.例题5答案:如图所示:(答案不唯一)奇点数: (0) (2) (2) (4) 偶点数: (4) (4) (5) (5) 能否一笔画成: (√) (√) (√) (×)详解:图中有4个奇点,不能一笔画成.去掉或添加一条线使得奇点个数减少,那么就在2个奇点之间去掉或添加线. 6.例题6 答案:甲详解:先把这个送货路线图画成“点线图”,如图所示,A 、C 是奇点.所以,甲从A 点出发回到C 点,可以一次不重复的走遍所有的街道;而乙要走遍所有的街道,其中必有重复.所以甲先回到C 点.7.练习1答案:√,√,√,×,×,√,√简答:第2个图形和第5个图形是非连通图,不能一笔画成;其它是连通图,依次尝试判断即可. 8.练习2答案:如图所示:简答:先把交叉点是奇点的圈起来,一一数出来,再判断能否一笔画成.(1) (2)(3)(4)奇点数: (0) (2) (2) (6) 偶点数: (3) (2) (3) (1) 能否一笔画成: (√) (√) (√) (×)9. 练习3答案:A 点或F 点简答:图中A 点和F 点是奇点,其它交叉点都是偶点.有2个奇点的图形,一笔画的特征是:从图形的一个奇点出发,回到另一个奇点.只有从奇点的路口出发,才能一次不重复地走遍所有小路.所以小乖应该从A 点或F 点出发.10. 练习4答案:C 或D简答:把图中的平面图画成“点线图”,如图所示,C 点和D 点是奇点,所以蘑菇园的小朋友们从C 或D 入口出发,才能一次不重复地走遍游乐场内的所有小路.11. 作业1 答案:×,×,√,×,√,√简答:第1个图形是非连通图,不能一笔画成;其它是连通图,依次尝试判断即可.12. 作业2答案:如图所示:简答:先把交叉点是奇点的圈起来,一一数出来,再判断能否一笔画成.13. 作业3答案:A 或B简答:观察图形可知,图中只有A 和B 两个奇点,其余的都是偶点.走时必须从一个奇点出发到另一个奇点结束,也就是从A 出发,从B 离开,或者从B 出发,从A 离开.14. 作业4答案:灰鼠和小熊简答:先根据果园的平面图画出点线图,如下图所示.观察下图中共有9个交叉点,其中7个点是偶点,只有两奇点数: (2) (4) (0) (4) 能否一笔画: (√) (×) (√) (×)(1) (2) (3) (4)E个点(北、西)是奇点,所以只有在北门和西门的小动物可以不重复地一次走遍所有的小路.15.作业5答案:不能简答:在任意两个奇点之间添一条线或去一条线,如下图所示,都可以改成能一笔画成的图形(答案不唯一).小猪(东)小象(南)。


一笔画(奥数)一笔画【知识要点】1.概念:一笔画是指笔不离开纸,而且每条线都只画一次不准重复而画成的图形。
2.分类:图中的点可分两大类:(1)双数点:从这点出发的线的数目是双数的,叫双数点。
(2)单数点:从这点出发的线的数目是单数的,叫单数点。
3.规律:一个图形能否一笔画成,关键在于图中单数点的多少。
(1)凡是图形中没有单数点的一定可以一笔画成。
(2)凡是图形中只有两个单数点,一定可以一笔画成,画时必须从一个单数点为起点,最后以另一单数点为终点。
(3)凡是图形中单数点的个数多于两个时,此图肯定是不能一笔画成。
【题目】1 判断下面图形中哪些点是单数点哪些点是双数点。
2 下列图形中各有几个单数点?能一笔画成吗?3 判断下面图形能不能一笔画成?如果能,应该怎样画?4下面图形能不能一笔画成?这什么?ADEA B CC A B A B C DE F ADCBB C A5 如图是一个大型花池中小路的平面图,你能否不重复地一次走完所有的小路?进出口应设在什么地方?6 将下图加上最少的线改成一笔画的图形。
7.将下图去掉最少的线改成一笔画图形。
8.下图中的线段代表小路,请小朋友想一想,能够不重复地爬遍小路的甲蚂蚁还是乙蚂蚁?该怎么爬?9.为迎接2008年奥运会在北京召开,你能一笔画出奥运会的五环图案吗?10.下图是一个公园的平面图,应怎样走才能使游客走通每条路而不重复,设计一条最佳路线。
11 一个公园的平面图如下,请你设计好入口、出口,并给出一条浏览路线,要求走遍每一条路且不重复。
12不重复。
A BHCG FE D13.如图,是一个名画展厅的平面图,要使参观者不重复地走遍每一条画廊,问:出口、入口应设在哪里?14.黑色的鱼与白色的鱼所能游动的河道如下图所示。
黑色的鱼在A 点位置,白色的鱼在B 点位置。
哪条鱼能不重复地游遍所有的河道?15.能用一根铁丝弯成下面的图形吗?16.一个邮递员投递信件要走的街道如图,为节约时间,他想自己设计一条线路,可以不重复的走遍每一条街道,你能帮帮他吗?17.一只蚂蚁要想不重复的爬遍每一条线路,应从哪里出发,到哪里结束?18.你能用一笔画成4条线段把下图的9个点都连起来吗?19.下图能否一笔画成?如果能,应怎样画?20.如图,在一个六面体的顶点A 和B 处各有一只蜗牛,它们比赛看谁能不重复地爬遍每一棱线到达C点。


小学奥数:一笔画
【专题简析】
1.概念:一笔画是指笔不离开纸,而且每条线都只画一次不准重复而画成的图形。
2.图中的点可分两大类:
(1)双数点:从这点出发的线的数目是双数的,叫双数点。
(2)单数点:从这点出发的线的数目是单数的,叫单数点。
3.规律----一个图形能否一笔画成,关键在于图中单数点的多少。
(1)凡是图形中没有单数点的一定可以一笔画成。
(2)凡是图形中只有两个单数点,一定可以一笔画成,画时必须从一个单数点为起点,
最后以另一单数点为终点。
(3)凡是图形中单数点的个数多于两个时,此图肯定是不能一笔画成。
【题目】
1 判断下面图形中哪些点是单数点哪些点是双数点。
单数点( ) ( ) ( ) ( ) ( ) ( ) ( )
双数点( ) ( ) ( ) ( ) ( ) ( ) ( )
单数点( ) ( ) ( )
双数点( ) ( ) ( )
A
B
E
A B
C
B
单数点( ) ( ) ( ) 双数点( ) ( ) ( )
单数点( ) ( ) ( )
双数点( ) ( ) ( )
单数点( ) ( ) ( )
双数点( ) ( ) ( )
由以上图形可以得出:
B
C
A
C
单数点()()()双数点()()()
单数点()()()
双数点()()()
由以上图形可以得出:
C D
E
F
单数点()()()双数点()()()
单数点()()()双数点()()()由以上图形可以得出:。
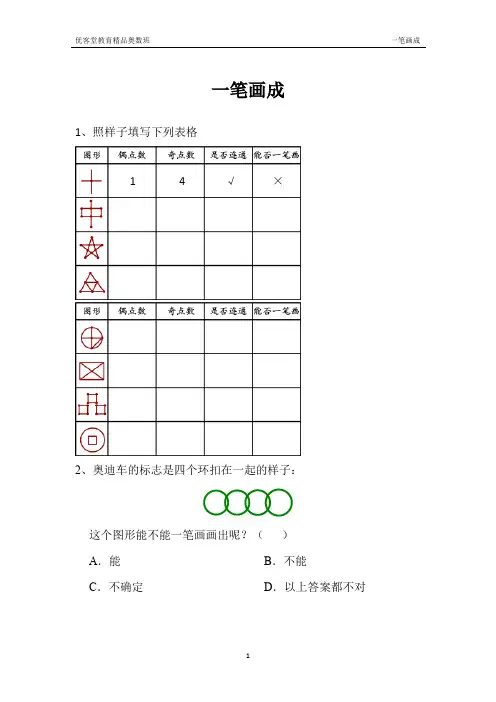
一笔画成
1、照样子填写下列表格
2、奥迪车的标志是四个环扣在一起的样子:
这个图形能不能一笔画画出呢?( )
A .能
B .不能
C .不确定
D .以上答案都不对
3、下列图形能一笔画成吗?下面说法正确的是(
) 1 4 √ ×
A.能一笔画出,因为有偶数个奇点。
B.能一笔画出,因为没有奇点。
C.不能一笔画出,因为有6个奇点。
D.不能一笔画出,因为有4个奇点。
4、下图是小光家的平面图,小光想从某个房间出发,一次性不重复的穿过所有门,最后到达F房间,那么他可以从()房间出发?(2014年数学解题能力展示中年级组复赛)
5、下列图中,哪些可以一笔画成?()。

小学奥数:一笔画
【专题简析】
1.概念:一笔画是指笔不离开纸,而且每条线都只画一次不准重复而画成的图形。
2.图中的点可分两大类:
(1)双数点:从这点出发的线的数目是双数的,叫双数点。
(2)单数点:从这点出发的线的数目是单数的,叫单数点。
3.规律----一个图形能否一笔画成,关键在于图中单数点的多少。
(1)凡是图形中没有单数点的一定可以一笔画成。
(2)凡是图形中只有两个单数点,一定可以一笔画成,画时必须从一个单数点为起点,最后以另一单数点为终点。
(3)凡是图形中单数点的个数多于两个时,此图肯定是不能一笔画成。
【题目】
1判断下面图形中哪些点是单数点哪些点是双数点。
单数点()()()()()()()双数点()()()()()()()
单数点()()()
双数点()()()
A
B
E A
B C
B
单数点( ) ( ) ( ) 双数点( ) ( ) ( )
单数点( ) ( ) ( )
双数点( ) ( ) ( )
单数点( ) ( ) ( )
双数点( ) ( ) ( )
由以上图形可以得出:
B C
A
C B A
单数点( ) ( ) ( )
双数点( ) ( ) ( )
单数点( ) ( ) ( )
双数点( ) ( ) ( )
由以上图形可以得出:
A C
D E F
单数点()()()双数点()()()
单数点()()()双数点()()()由以上图形可以得出:。
小学奥数:一笔画【专题简析】1.概念:一笔画是指笔不离开纸,而且每条线都只画一次不准重复而画成的图形。
2.图中的点可分两大类:(1)双数点:从这点动身的线的数量是双数的,叫双数点。
(2)单数点:从这点动身的线的数量是单数的,叫单数点。
3.规律----一个图形可否一笔画成,关键在于图中单数点的多少。
(1)凡是图形中没有单数点的必然能够一笔画成。
(2)凡是图形中只有两个单数点,必然能够一笔画成,画时必需从一个单数点为起点, 最后以另一单数点为终点。
(3)凡是图形中单数点的个数多于两个时,此图确信是不能一笔画成。
【题目】1 判定下面图形中哪些点是单数点哪些点是双数点。
单数点( ) ( ) ( ) ( ) ( ) ( ) ( )双数点( ) ( ) ( ) ( ) ( ) ( ) ( )单数点( ) ( ) ( )双数点( ) ( ) ( )2 、下列图形中各有几个单数点?能一笔画成吗?ABEA BCB A单数点( ) ( ) ( ) 双数点( ) ( ) ( )单数点( ) ( ) ( )双数点( ) ( ) ( )单数点( ) ( ) ( )双数点( ) ( ) ( )由以上图形能够得出:3、下列图形中各有几个单数点?能一笔画成吗?CD EFBCAC单数点()()()双数点()()()单数点()()()双数点()()()由以上图形能够得出:3、下列图形中各有几个单数点?能一笔画成吗?单数点()()()双数点()()()单数点()()()双数点()()()由以上图形能够得出:。