小学二年级奥数 一笔画

一笔画问题发现不同知识框架如果用笔在纸上连续不断又不重复，一笔画成某种图形，这种图形就叫一笔画。

那么是不是所有的图形都能一笔画成呢？这一讲我们就一起来学习一笔画的规律。

能否一笔画成，先看是不是连通图形，不连通图形一定不能一笔画成。

连通图形，关键在于判别奇点、偶点的个数。

一、只有偶点，可以一笔画，并且可以以任意一点作为起点。

二、只有两个奇点，可以一笔画，但必须以这两个奇点分别作为起点和终点。

三、奇点超过两个，则不能一笔画。

对于一些比较复杂的路线问题，可以先转化为简单的几何图形，然后根据判定是否能一笔画的方法进行解答。

例题精讲【例1】下面这些图形，哪个能一笔画？哪个不能一笔画？（1）（2）（3）（4）【例2】下面这些图形，哪个能一笔画？哪个不能一笔画？（1）（2）（3）（4）【例3】下面的各个小图形都是由点和线组成的．请你仔细观察后回答：①与一条线相连的有哪些点?②与二条线相连的有哪些点?③与三条线相连的有哪些点?④与四条线或四条以上的线相连的有哪些点?【例4】下面各图能否一笔画成？（1）（2）（3）【例5】下面这几个字都能一笔写出来吗?【例6】下面这几个字母都能一笔写出来吗?【例7】下面的图形，哪些能一笔画出？哪些不能一笔画出？【例8】下图中，至少要画几笔才能画成？【随练1】德国有个城市叫哥尼斯堡．城中有条河，河中有个岛，河上架有七座桥，这些桥把陆地和小岛连接起来，这样就给人们提供了一个游玩的好去处(见下图)．俗话说，“人是万物之灵”，他们就是在游玩时候想出了这样一个问题：如果在陆地上可以随便走，而对每座桥只许通过一次，那么一个人要连续地走完这七座桥怎么个走法? 好动脑筋的小朋友请先不要接着往下读，你也试一试，走一走．AB CD课堂检测【随练2】 在我国著名数学家陈景润写的《数学趣谈》一书中，有下面的这样一道题，大意是说：在法国的首都巴黎有一条河，河中有两个小岛，那里的人们建了15座桥把两个小岛和河岸连接起来，如下图所示，请你说一说，从任一岸出发，一次连续地通过所有的桥到达另一岸，可能吗?(每座桥只能走一次)【作业1】 下面的图形都是由点和线组成的．请你仔细观察后回答： ①与一条线相连的有哪些点? ②与三条线相连的有哪些点?③与四条线或四条以上的线相连的有哪些点?【作业2】 下面各图能否一笔画成？PONMLKJIHGFEDCBA家庭作业（1）（2）（3）（4）【作业3】下面这几个字母都能一笔写出来吗?【作业4】下面这几个字都能一笔写出来吗?【作业5】下图中，至少要画几笔才能画成？。

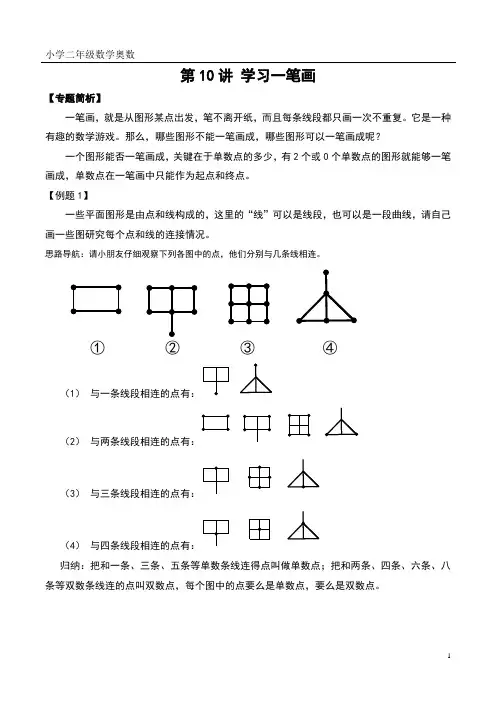
第10讲学习一笔画【专题简析】一笔画，就是从图形某点出发，笔不离开纸，而且每条线段都只画一次不重复。

它是一种有趣的数学游戏。

那么，哪些图形不能一笔画成，哪些图形可以一笔画成呢？一个图形能否一笔画成，关键在于单数点的多少，有2个或0个单数点的图形就能够一笔画成，单数点在一笔画中只能作为起点和终点。

【例题1】一些平面图形是由点和线构成的，这里的“线”可以是线段，也可以是一段曲线，请自己画一些图研究每个点和线的连接情况。

思路导航：请小朋友仔细观察下列各图中的点，他们分别与几条线相连。

①②③④（1）与一条线段相连的点有：（2）与两条线段相连的点有：（3）与三条线段相连的点有：（4）与四条线段相连的点有：归纳：把和一条、三条、五条等单数条线连得点叫做单数点；把和两条、四条、六条、八条等双数条线连的点叫双数点，每个图中的点要么是单数点，要么是双数点。

1.任意找一个平面图形，数一数图中有几个单数点，几个双数点。

2.下面图形中有哪几个单数点？B3.数一数下面图形中有几个双数点，分别是哪些点？B【例题2】下面的图形能不能一笔画成？如果能，应该怎样画？（1） O（2）B D（3）【思路导航】图（1）中A 、B 、C 、D 、O 五个点都是双数点，所以这个图形可以一笔画成。

画时可以从任意一点出发。

图（2）中A 、C 、D 、F 四个点都是双数点，B 和E 两个点是单数点，所以这个图形也可以一笔画成。

画时要从单数点出发，最后回到另一个单数点。

图（3）中A 、D 是双数点，B 、C 、E 和F 四个点是单数点，单数点的个数超过了两个，这个图形不能一笔画成。

1.下面的图形能不能一笔画成，如果能，请说明画法，如果不能，请说明理由（1）（2）2.下列图形能一笔画成吗?为什么？3.观察下列图形，哪个图形可以一笔画成？怎么画？【例题3】下图是某地区所有街道的平面图，甲、乙两人同时分别从A、B出发，以相同的速度走遍所有的街道，最后到达C.那么两人谁先到达？C思路导航：题中要求两人必须走遍所有街道，最后到达C.仔细观察，可以发现图中有两个单数点：A 、C 。

一笔画月日姓名【知识要点】1．概念：一笔画是指笔不离开纸，而且每条线都只画一次不准重复而画成的图形。

2．分类：图中的点可分两大类：（1）双数点：从这点出发的线的数目是双数的，叫双数点。

（2）单数点：从这点出发的线的数目是单数的，叫单数点。

3．规律：一个图形能否一笔画成，关键在于图中单数点的多少。

（1）凡是图形中没有单数点的一定可以一笔画成。

（2）凡是图形中只有两个单数点，一定可以一笔画成，画时必须从一个单数点为起点，最后以另一单数点为终点。

（3）凡是图形中单数点的个数多于两个时，此图肯定是不能一笔画成。

【典型例题】例1．判断下面图形中哪些点是单数点，哪些点是双数点。

例2．下列图形中各有几个单数点？能一笔画成吗？（1）（2）（3）（4）例3．如图，能不能一笔画成？如果能，应该怎样画？例4．将下图去掉最少的线改成一笔画图形。

随堂小测姓名成绩1.判断下面图形哪些是单数点，哪些是双数点。

2. 下列图形中各有几个单数点？能一笔画成吗？3. 一个邮递员投递信件要走的街道如下左图，为节约时间，他想自己设计一条线路，可以不重复的走遍每一条街道，你能帮帮他吗？4. 一只蚂蚁要想不重复的爬遍每一条线路，应从哪里出发，到哪里结束？（3）AC E（1）（2）（3）（4）5. 将下图加上最少的线改成一笔画的图形。

【知识拓展】1．为迎接2008年奥运会在北京召开，你能一笔画出奥运会的五环图案吗？2．你能用一笔画成4条线段把下图的9朵小花都连起来吗？课后作业姓名成绩1．判断下面图形中哪些点是单数点哪些点是双数点。

2．判断下面图形能不能一笔画成。

（1）（2）B3．下图能否一笔画成？如果能，应怎样画？4．如图，是一个公园的平面图，请你设计好入口、出口，并给出一种游玩路线，要求走遍每一条路且不重复。

5．如图，是一个名画展厅的平面图，要使参观者不重复地走遍每一条画廊，问：出口、入口应设在哪里？家长签名：【课外知识链接】七桥问题著名古典数学问题之一。

第八讲一笔画前续知识点：二年级第一讲；XX模块第X讲后续知识点：X年级第X讲；XX模块第X讲把里面的人物换成相应红字标明的人物．这里是小区平面图，我从哪个入口进去，才能一次不重复地走遍小区的所有小路，尽快地把口罩送给每个朋友呢？由于空气污染严重，哥哥让我给朋友们去送口罩，以防大家得病。

墨莫墨莫一笔画，是指从连通图的一点出发，笔不离纸，每条线都只画一次，不能重复．一笔画能解决很多实际问题．那么什么样的图形能够一笔画成，什么样的图形不能一笔画成呢？试着画一画下面的图形吧！例题1观察下列图形，能一笔画成的打“√”，不能一笔画成的打“×”．（）（）（）（）（）（）【提示】动手画一画，你知道什么样的图形一定不能一笔画成吗？练习1观察下列图形，能一笔画成的打“√”，不能一笔画成的打“×”．（）（）（）（）（）（）（）（）我们画了这么多图形，不难发现，不连通的图形一定不能一笔画成，能一笔画成的图形必定是连通图．连通图，指的是如果一个图形中的任意两点都是连通的，那么这个图形就是连通图．一个图形可以一笔画成，除了必须是连通图，还有没有其它的规律和特点呢？我们一起找找吧！首先，我们先来认识下面的两个名词：从一点出发的线条数目是奇数，如1、3、5、7、……我们称它为奇点． 从一点出发的线条数目是偶数，如2、4、6、8、……我们称它为偶点．奇点、偶点的个数与一个图形能否一笔画成有什么关系呢？我们来看一看下面的题目吧！【例题2】下面的各个图形都是由点和线组成的．请你仔细观察后回答，各图中的交叉点分别有几个奇点？几个偶点？能否一笔画成？能的在“（ ）”里打“√”，不能的在“（ ）”里打“×”．【提示】从某一点发出奇数条线，这个点是奇点；从某一点发出偶数条线，这个点是偶点．【练习2】下面的各个图形都是由点和线组成的．请你仔细观察后回答，各图中的交叉点分别有几个奇点？几个偶点？能否一笔画成？能的在“（ ）”里打“√”，不能的在“（ ）”里打“×”．（1） （2） （3）（4） 奇点数： （ ） （ ） （ ） （ ） 偶点数： （ ） （ ） （ ） （ ） 能否一笔画成：（ ） （ ） （ ） （ ）奇点数： （ ） （ ） （ ） （ ） 偶点数： （ ） （ ） （ ） （ ）能否一笔画成：（ ） （ ） （ ） （ ）（1） （2）（3） （4）通过对上题的观察，相信大家都发现了规律．有0个奇点的连通图能够一笔画成．画时可以以任一点为起点，最后一定能以这个点为终点画完此图． 有2个奇点的连通图能够一笔画成．画时必须以一个奇点为起点，另一个奇点为终点画完此图． 有2个以上奇点的连通图不能一笔画成．根据以上规律，我们可以通过奇点个数来正确判断哪些图形能一笔画成，哪些图形不能一笔画成．我们就用学到的知识来解决生活中的一笔画问题吧！例题3草地上有许多小路，丁丁和月月分别站在A 、B 两个路口．谁能够一次不重复地走遍所有小路？【提示】谁的出发点是奇点？练习3花园里有许多崎岖的小路，小乖要浇花，它想一次不重复地走完每条小路．该从哪个路口出发呢？AB CDE例题4小河中有4个小岛，小岛之间建有六座桥．淘淘能一次不重复地走遍所有的小桥吗？【提示】先把实际地图画成“点线图”，然后数数奇点的个数吧！练习4蘑菇园的小朋友们要去游乐场玩，他们可以从6个入口进出游乐场．他们从哪个入口出发，才能一次不重复地走遍游乐场内的所有小路？我们已经可以正确判断哪些图形可以一笔画成，哪些不能一笔画成．如果不能一笔画成，可不可以通过增添或删除一些线的方法，让它变成可以一笔画成的图形呢？例题5AB C D EFG下面的“蝴蝶”能一笔画成吗？如果不能，按照如下要求把它改成能一笔画成的图形．（1）在图1中，去掉一条线；（2）在图2中，添加一条线．图1图2【提示】在两个奇点之间去掉或添加线．例题6甲乙两个不同公司的快递员去送货，两人都要以同样的速度走遍所有的街道（阴影部分），甲从A点出发，乙从B点出发，最后都回到C点．如果都选择最短的线路，谁先回到C点？ABC【提示】先把实际道路图画成“点线图”，再判断各个交叉点中有哪些是奇点．课堂内外七桥问题德国有一个城市叫哥尼斯堡．城中有一条小河，河中有两个小岛，还有7座桥把这两个小岛和陆地连接起来，如下图所示．人们经常在这里游玩，他们在游玩的时候提出这样一个问题：能不能一次不重复地走遍所有的小桥呢？作业1. 观察下列图形，能一笔画成的打“√”，不能一笔画成的打“×”．2. 下面每幅图中的交叉点分别有几个奇点？能否一笔画成呢？能的在“（ ）”里打“√”，不能的在“（ ）”里打“×”．（ ） （ ） （ ）（ ） （ ） （ ）小岛 小岛3. 菲菲周末去郊外的公园玩，公园里有许多崎岖的小路．她想不重复地一次走完每条小路，可以从哪个路口出发？4. 小熊、灰鼠、小象和小猪要分别从东、南、西、北四个入口去果园采果子，谁能不重复地一次走遍所有小路？5. 下面的图形能一笔画成吗？如果不能，按照如下要求将其改成能一笔画成的图形．（1）在图1中去掉一条线；（2）在图2中添加一条线．图1图2北CD E F G HBA 奇点数： （ ） （ ） （ ） （ ） 能否一笔画：（ ） （ ） （ ） （ ）（1） （2） （3） （4）第八讲 一笔画1.例题1答案：×，√，√，×，×，√详解：第（1）个图形是非连通图，不能一笔画；其它都是连通图，依次尝试判断即可． 2.例题2答案：如图所示：详解：把交叉点是奇点的圈起来，如图所示：有0个奇点和2个奇点的连通图能够一笔画成；2个奇点以上的连通图不能一笔画成．一个图形能否一笔画成与偶点数无关． 3.例题3 答案：月月详解：图中B 点和E 点是奇点，其它交叉点都是偶点．有2个奇点的图形，一笔画的特征是：从图形的一个奇点出发，回到另一个奇点．只有从奇点的路口出发，才能一次不重复地走遍所有小路．美羊羊站在B 点的路口上，所以能够一次不重复地走遍所有小路． 4.例题4 答案：不能详解：把图中的小岛看成点，把桥看成线，得到“点线图”，如图所示，有4个交叉点，这4个交叉点都是奇点，这个图形不能一笔画成．所以淘淘不能一次不重复地走遍所有的小桥．5.例题5答案：如图所示：（答案不唯一）奇点数： （0） （2） （2） （4） 偶点数： （4） （4） （5） （5） 能否一笔画成： （√） （√） （√） （×）详解：图中有4个奇点，不能一笔画成．去掉或添加一条线使得奇点个数减少，那么就在2个奇点之间去掉或添加线． 6.例题6 答案：甲详解：先把这个送货路线图画成“点线图”，如图所示，A 、C 是奇点．所以，甲从A 点出发回到C 点，可以一次不重复的走遍所有的街道；而乙要走遍所有的街道，其中必有重复．所以甲先回到C 点．7.练习1答案：√，√，√，×，×，√，√简答：第2个图形和第5个图形是非连通图，不能一笔画成；其它是连通图，依次尝试判断即可． 8.练习2答案：如图所示：简答：先把交叉点是奇点的圈起来，一一数出来，再判断能否一笔画成．（1） （2）（3）（4）奇点数： （0） （2） （2） （6） 偶点数： （3） （2） （3） （1） 能否一笔画成： （√） （√） （√） （×）9. 练习3答案：A 点或F 点简答：图中A 点和F 点是奇点，其它交叉点都是偶点．有2个奇点的图形，一笔画的特征是：从图形的一个奇点出发，回到另一个奇点．只有从奇点的路口出发，才能一次不重复地走遍所有小路．所以小乖应该从A 点或F 点出发．10. 练习4答案：C 或D简答：把图中的平面图画成“点线图”，如图所示，C 点和D 点是奇点，所以蘑菇园的小朋友们从C 或D 入口出发，才能一次不重复地走遍游乐场内的所有小路．11. 作业1 答案：×，×，√，×，√，√简答：第1个图形是非连通图，不能一笔画成；其它是连通图，依次尝试判断即可．12. 作业2答案：如图所示：简答：先把交叉点是奇点的圈起来，一一数出来，再判断能否一笔画成．13. 作业3答案：A 或B简答：观察图形可知，图中只有A 和B 两个奇点，其余的都是偶点．走时必须从一个奇点出发到另一个奇点结束，也就是从A 出发，从B 离开，或者从B 出发，从A 离开．14. 作业4答案：灰鼠和小熊简答：先根据果园的平面图画出点线图，如下图所示．观察下图中共有9个交叉点，其中7个点是偶点，只有两奇点数： （2） （4） （0） （4） 能否一笔画： （√） （×） （√） （×）（1） （2） （3） （4）E个点（北、西）是奇点，所以只有在北门和西门的小动物可以不重复地一次走遍所有的小路．15.作业5答案：不能简答：在任意两个奇点之间添一条线或去一条线，如下图所示，都可以改成能一笔画成的图形（答案不唯一）．小猪（东）小象（南）。

文档仅供参考文档仅供参考第10讲 学习一笔画【专题简析】一笔画,就是从图形某点出发,笔不离开纸,而且每条线段都只画一次不重复. 它是一种有趣的数学游戏. 那么,哪些图形不能一笔画成,哪些图形可以一笔画成呢？哪些图形可以一笔画成呢？一个图形能否一笔画成,关键在于单数点的多少,有2个或0个单数点的图形就能够一笔画成,单数点在一笔画中只能作为起点和终点. 【例题1】一些平面图形是由点和线构成的,这里的“线”可以是线段,也可以是一段曲线,请自己画一些图研究每个点和线的连接情况.思路导航：请小朋友仔细观察下列各图中的点,他们分别与几条线相连.① ② ③ ④（1） 与一条线段相连的点有：（2） 与两条线段相连的点有：（3） 与三条线段相连的点有：（4） 与四条线段相连的点有：归纳：把和一条、三条、五条等单数条线连得点叫做单数点；把和两条、四条、六条、八条等双数条线连的点叫双数点,每个图中的点要么是单数点,要么是双数点. 练习11.任意找一个平面图形,数一数图中有几个单数点,几个双数点.2.下面图形中有哪几个单数点？下面图形中有哪几个单数点？CBA D3.数一数下面图形中有几个双数点,分别是哪些点？分别是哪些点？F E D BA C HG【例题2】下面的图形能不能一笔画成？如果能,应该怎样画？应该怎样画？A C A BC （1） O （2）BD D EF A BCC （3）D EF 【思路导航】图（1）中A 、B 、C 、D 、O 五个点都是双数点,所以这个图形可以一笔画成.画时可以从任意一点出发. 图（2）中A 、C 、D 、F 四个点都是双数点,B 和E 两个点是单数点,所以这个图形也可以一笔画成. 画时要从单数点出发,最后回到另一个单数点. 图（3）中A 、D 是双数点,B 、C 、E 和F 四个点是单数点,单数点的个数超过了两个,这个图形不能一笔画成.练习21.下面的图形能不能一笔画成,如果能,请说明画法,如果不能,请说明理由请说明理由（1） （2）2.下列图形能一笔画成吗?为什么？为什么？3.观察下列图形,哪个图形可以一笔画成？怎么画？哪个图形可以一笔画成？怎么画？【例题3】下图是某地区所有街道的平面图,甲、乙两人同时分别从A、B出发,以相同的速度走遍所有的街道,最后到达C.那么两人谁先到达？那么两人谁先到达？BC A思路导航：题中要求两人必须走遍所有街道,最后到达C.仔细观察,可以发现图中有两个单数点：A、C. 这就是说：甲可以从A点出发,不重复地走遍所有街道,最后到达C.而B点是双数点,从B点出发的乙则不行. 因此,甲所走的路程正好等于所有街道的总和,而乙所走的路程一定比这个总和多,所以甲最先到达C.解：甲最先到达C.BA CBCA1.下图是某新村小区主干道平面图. 甲、乙两人同时分别从A 、B 出发,以相同的速度走遍所有的主干道,最后到达C.问谁能最先到达C?2. 甲、乙两辆车同时以相同的速度分别从A 、B 出发,哪辆车能最先行驶完所有的路程？哪辆车能最先行驶完所有的路程？A BC3.一只蚂蚁分别从A 点和B 点出发,爬遍所有的小路. 如果每次爬行的速度相同,那么从哪一点出发所用的时间少？出发所用的时间少？【例题4】下图（图1）能否一笔画成,若不能,你能用什么方法把它改成能够一笔画成的图形？你能用什么方法把它改成能够一笔画成的图形？（1） （2）思路导航：此图共有9个点,其中5个点是双数点,4个点是单数点,由于超过两个单数点,因此不能一笔画成. 要想改为一笔画成,关键在于减少单数点数目（把单数点的个数减少到0或2）,所以只要在任意两个单数点间连上线,就可以一笔画,有时也可以将多余的两个单数点间的连线去掉,改成一笔画.解：图（1）有4个单数点,不能一笔画成. 要改成一笔画成,如图（2）1.将下图改成一笔画.1.2.3.在一个小区中有一些路,每个圆柱表示邮筒（如下图）,邮递员叔叔每次送信时,总是没法走过每一条路而又不重复,你知道为什么吗？如果请你给小区加一条路来解决这个问题,你准备把这条路加在哪儿？请你动手画一画.【例题5】邮递员叔叔要给一个居民小区送信（如图）,怎么走才能少走重复路,使每天走的路尽可能短？使每天走的路尽可能短？IAGECH D BF思路导航：图中一共有九个点,其中单数点有2个（点D 和点F ）,因此能一次不重复走过所有的路,但必须从这两个单数点中的一个出发,再回到另一个单数点.解：邮递员叔叔只能从点D （或点F ）出发,走过所有的路后,再回到点F(或点D) .1.下图是以个小区的中心花园的平面图,你能一次不重复地走完所有的路吗？入口和出口应该设在哪儿呢？设在哪儿呢？2.园林工人在花园里浇花,怎样才能不重复地走遍每条小路？怎样才能不重复地走遍每条小路？3. 下图是“儿童乐园”平面图,出、入口应分别设在哪里才能不重复地走遍每条路？可以怎么走？走？DC A B【拓展提高】【拓展提高】1、下面的图形能不能一笔画成？为什么？如果能,应该怎样画？应该怎样画？3、小明和玲玲玩“过木桥”的游戏（如下图）,他们谁能不走重复的路？他们谁能不走重复的路？ 小明小明玲玲玲玲4、在王大爷家的花园中有一些路（如下图）,王大爷每次给花浇水时,总是没法走过每一条路而又不重复,你知道为什么吗？如果请你给花园加一条路来解决这个问题,你准备把这条路加在哪儿？请你动手画一画.间隔趣谈【专题简析】两根绳子结起来只要打一个结两根绳子结起来只要打一个结,,两根绳子结成一个圆需要打两个结两根绳子结成一个圆需要打两个结,,一根绳子剪4次被剪成了5段等等段等等,,这是日常生活中的比较特殊的问题这是日常生活中的比较特殊的问题. . 想要做好这类题想要做好这类题,,需要我们多动脑筋需要我们多动脑筋,,多动笔画画笔画画,,才能找到正确的答案才能找到正确的答案. . 这一讲是有关绳子打结和剪绳子的问题这一讲是有关绳子打结和剪绳子的问题. . 给绳子打结如果不练成一个圆不练成一个圆,,打结的次数比绳子的根数少1；如果结成1个圆个圆,,打结的次数与绳子的根数同样多样多. . 同样同样,,如果是剪绳子如果是剪绳子,,那么剪成的段数比剪得次数多1. 【例题1】小刚把4根绳子连起来成一条绳子,一共需要打几个结？ 思路导航思路导航::解这种题解这种题,,可以画图解答可以画图解答. . 如图：如图：打结打结打结从上图中可以看出从上图中可以看出,4,4根绳子要结起来成一根绳子根绳子要结起来成一根绳子,,只要打3次结就可以了次结就可以了,,可见可见,,打结的次数比绳子的根数少1.解：解：4-1=34-1=34-1=3（个）（个）（个）答：小刚把4根绳子连起来成一条绳子根绳子连起来成一条绳子,,一共需要打3个结个结练习11．小明把5根绳子连起来成一根长绳根绳子连起来成一根长绳,,一共需要打几个结？一共需要打几个结？2.2.把把8根绳子连接起来成一根绳子根绳子连接起来成一根绳子,,一共需要打几个结？一共需要打几个结？【例题2】把几根绳子打7个结就能成一个圆？个结就能成一个圆？思路导航思路导航::根据题意根据题意,,如图所示：打了7个结个结,,就把一些绳子就把一些绳子 结成了一个圆结成了一个圆,,这些绳子应该有7根. 因此因此,,如果把绳子结成圆如果把绳子结成圆 时,绳子的根数与打结的次数相等绳子的根数与打结的次数相等. . 解：把7根绳子打7个结就能成一个圆个结就能成一个圆练习21．丽丽打了8个结就把一些绳子结成一个圆个结就把一些绳子结成一个圆,,你知道丽丽拿了几根绳子吗？你知道丽丽拿了几根绳子吗？2．小红拿10根绳子结成一个圆根绳子结成一个圆,,她打了几个结？她打了几个结？3．把20根绳子连接起来成一根绳子根绳子连接起来成一根绳子,,一共需要打几个结？如果要结成一个圆一共需要打几个结？如果要结成一个圆,,需要结几次？需要结几次？【例题3】一根10米长的绳子剪了4次,平均每段长多少米？平均每段长多少米？思路导航思路导航:10:10米长的绳子剪了4次,应该剪成了5段. 求平均每段长多少米求平均每段长多少米,,也就是要把10平均分成5份,求每份是多少求每份是多少. . 2510=¸（米）（米）,,因此平均每段长2米解：解：4+1=54+1=54+1=5（段）（段）（段） 2510=¸（米）（米）答：平均每段长2米 练习31．一根8米长的绳子米长的绳子,,剪了3次,平均每段长多少米？平均每段长多少米？2．一根9分米长的绳子分米长的绳子,,剪了2次,平均每段长多少分米？平均每段长多少分米？3．一根绳子剪了5次后次后,,平均每段长3米,这根绳子原来长多少米？这根绳子原来长多少米？【例题4】一根10米长的绳子米长的绳子,,把它剪成2米长的一段米长的一段,,可以剪多少段？要剪几次？可以剪多少段？要剪几次？ 思路导航思路导航::（1）10米长的绳子米长的绳子,,剪成每段2米长米长,,要求可剪多少段要求可剪多少段,,这里求10里面有几个2, 5210=¸（段）（段）,,可以剪5段.（2）要求剪几次）要求剪几次,,可以用线段图分析：可以用线段图分析：2米10米从图中可以看出每一段剪一次从图中可以看出每一段剪一次,,剪最后一次还可以有2段,因此剪的次数比剪得段数少1. 即剪得次数即剪得次数==段数段数-1. -1.解：5210=¸（段）（段） 5-1=4 5-1=4（次）（次） 答：可以剪5段,要剪4次. 练习41.1.一根木材长一根木材长8米,把它锯成2米长的小段米长的小段,,可以锯成多少段？要锯几次？2.2.一根一根12米长的铁丝米长的铁丝,,把它剪成3米长的小段米长的小段,,可以剪成多少段？要剪多少次？可以剪成多少段？要剪多少次？3.3.一根一根25米长的电线米长的电线,,剪了4次,可以剪成多少段？平均每段长多少米？可以剪成多少段？平均每段长多少米？【例题5】小兰在桌上摆小棒】小兰在桌上摆小棒,,先摆了1根,然后每隔7厘米放1根,在距离第一根42厘米处厘米处,,共放了几根？共放了几根？思路导航思路导航::每隔7厘米放一根厘米放一根,42,42里有几个7就有几段就有几段,42,42,42÷÷7＝6（段）（段）,,小棒的根数比段数多1,6+16+1＝＝7（根）（根）. . 解 :42÷7+1=77+1=7（根）（根）（根）练习51．小灰灰把贝壳放在桌上．小灰灰把贝壳放在桌上,,先放一个先放一个,,然后每隔4厘米放一个厘米放一个,,从第1个到20厘米处厘米处,,一共可以放多少个？以放多少个？2.2.小红把几枝铅笔放在桌上小红把几枝铅笔放在桌上小红把几枝铅笔放在桌上,,每两枝之间相隔8厘米厘米,,从第一根到最后一根之间相隔64厘米厘米,,你知道放了几枝铅笔吗？你知道放了几枝铅笔吗？3.3.小美在桌上摆了小美在桌上摆了1颗珠子颗珠子,,然后每隔5厘米放1颗,在距第一颗35厘米处放的是第几颗？厘米处放的是第几颗？练习题答案练习题答案练习11.4个2.7个练习21.8根2.10个3.19个 20次 练习31.2米2.3分米分米3.18 3.18米 练习41.81.8÷÷2＝4（段）（段）44－1＝3（次）（次）2.122.12÷÷3＝4（段）（段） 4 4－1＝3（次）（次）3.4+13.4+1＝＝5（段）（段） 25 25÷5＝5（米）（米） 练习51.201.20÷÷4+14+1＝＝6（个）（个）2.642.64÷÷8+18+1＝＝9（枝）（枝）3.353.35÷÷5+15+1＝＝8（颗）（颗）。