关于油藏的相渗曲线的以及含水饱和度曲线交点求法
- 格式:docx
- 大小:126.93 KB
- 文档页数:2




由相渗曲线推导含水与含水上升率关系公式1.根据油水两相渗流的达西定律,在不考虑毛管力和重力的情况下,含水率的公式为rwroo w w k k f •+=μμ11(1)得到:wow w rw ro f f k k μμ•-=1 (2)根据:w bs rwroae k k -= (3)那么: wow w bs rw ro f f ae k k w μμ•-==-1 从而:⎪⎪⎭⎫ ⎝⎛-•-=ww w ow f f a b s 1ln 1μμ (4)求导得:()w w w w f f b df ds -=111 (5) 所以: ()w w ww f bf ds df -=1 (6)2.由 ()()wc o w oi s B s B R ---=111 (7)求导:owc o oiw s B B ds dR -=11(8) 所以:()wc oio w s B BdR ds -=1 (9) 3.由式(6)和式(9)()()oiwc o w w w w w w B s B f bf dR ds ds df dR df -•-=•=11 所以,得出含水上升率与含水率的关系为()()w w oiwc o w f f B s B b dR df --=11 (10) 注水开发油田B oi ≈B o 则式(10)可化简为:()()w w wc wf f s b dRdf --=11 (11) 含水率与采出程度关系式推导由(7)式()()()()()()wc wc w wc w wc o w oi s s s s s s B s B R --=---≈---=1111111 (12) 得出()wc wc w s R s s +-=1 (13)则由(4)知 ()wc wc w w w o w s R s f f a b s +-=⎪⎪⎭⎫⎝⎛-•-=11ln 1μμ (14) 所以 ()[]wc wc s R s b oww e a f +--+=111μμ (15)式中:B oi 、B o ---------分别为原始和任一压力下的原油体积系数; K ro 、k rw ---------油、水的相对渗透率; f w ----------------含水率,小数或百分数; s wc --------------束缚水饱和度,小数或百分数; s w --------------含水饱和度,小数或百分数;μo 、μw -------地下油、水粘度,MP a ·s ; R ----------------采出程度,小数或百分数;备注:按《油藏工程基础》(郎兆新主编)第243页内容定义定义无因次采油指数和无因次采液指数为有因次的采油采液指数除以油藏初始时刻无水采油期的采油指数,其值应该等于产油量或产液量除以初始时刻的产油量。
关于油藏的相渗曲线的以及含水饱和度曲线交点求法小熊维尼在油藏的期末复习的时候,我就发现了这个问题,明明很正常的fw-Sw曲线,想当然的会以为直接对它求导,然后求得斜率相等的点就行了。
但是往往事与愿违,往往给出的是点的数据,就是测井数据。
那么我们怎么来精确地求得那个交点值呢,以下给出一种数值方法,希望对大家有用。
前期准备:你必须得有mathematical,matlab或者maple,当然如果你对自己的计算能力有信心,那也行的。
步骤:1,我们从Excel表格中读取数据(以下我以传姐的数据为例)2,对导入的数据进行插值(三次艾米尔特插值的精度就可以了),画出插值函数,即:这就是经过插值之后的fw-Sw曲线了,既然我们有了函数表达式,那么后面的步骤我相信很多人都明白了。
3,但是事情往往没这么简单,你可能会想:“对啊,我略懂mathematical或者matlab 我知道切点的斜率和切线的斜率相等,而且切线过(0.32,0)这个点,这个还不好求吗?不就是一个Solve命令嘛。
”如果你真要这么想,我只能表示呵呵了。
可以明确表示常规的解方程命令在这里都不起作用。
原因是你的曲线是插值分段函数,虽然你看起来就像一条完整的曲线一样。
4,穷则思变,我们采用的是牛顿切线法或者割线法,这是一种线性收敛的计算方法,但是对于这道题的要求够了。
在mathematical下命令是FindRoot,matlab我就不知道了(求教)。
本质上牛顿切线法是一种迭代方法,也就是说必须给出迭代初始点以上是mathematical下的FindRoot函数的调用格式,和普通解方程的格式一致,看看下面的例子就明白了5,通过这样的方法我们就可以得到交点的x数值了带入插值函数(就是上面的函数可以求得y值了。
这样就可以把切线完美的表达出来了(两个点了)。
如下图:以下是传姐同学的数据,大家可以先仿照做一遍,看看自己做对没有:。

油藏工程常用计算方法油藏工程是石油工程中的一个重要领域,涉及到油藏的勘探、开发和生产等方面。
在油藏工程中,常常需要进行一系列的计算来评估和分析油藏的性质和行为。
下面将介绍一些油藏工程常用的计算方法。
1.计算原油储量原油储量是评估一个油藏的重要参数,常用的计算方法有静态法和动态法。
静态法通过测井数据和油藏地质模型,计算储量的地质体积。
动态法则通过考虑地层渗流和流体流动的动态特性,计算储量的产油体积。
2.计算油藏含水饱和度油藏的含水饱和度是指油藏中含有的水的比例。
常用的计算方法有电测井测井曲线分析法和测井资料解释法。
通过分析不同测井曲线(如电阻率曲线、自然伽玛曲线等)的变化规律,可以计算油藏的含水饱和度。
3.计算油藏渗透率油藏渗透率是衡量油藏储层导流能力的重要指标。
常用的计算方法有试油法和渗透率曲线法。
试油法通过实验室试验或现场试油,测量岩心样品或井中液体在单位时间内通过单位面积的流量,计算渗透率。
渗透率曲线法则通过测井曲线分析,利用渗透率曲线的特征,计算渗透率。
4.计算油藏压力与产量关系油藏的压力与产量关系是研究和预测油藏开发效果的重要依据。
常用的计算方法有压力-产量分析和产能预测法。
压力-产量分析通过分析油藏生产数据和压力变化,建立压力与产量的关系。
产能预测法则通过考虑岩石物性和流体性质等因素,结合油藏地质特征和开发方案,预测不同开发阶段的产能。
5.计算水驱油效果水驱是油藏开发中常用的一种增产方法。
计算水驱油效果是评估水驱效果的重要手段。
常用的计算方法有位移效率法和水驱指数法。
位移效率法通过考虑水驱后的产量与无水驱时的产量之比,计算水驱效果。
水驱指数法则通过测量水驱前后的注水压力和油井生产的工况参数,计算水驱指数。
以上介绍了一些油藏工程中常用的计算方法,涉及到油藏储量、含水饱和度、渗透率、压力与产量关系和水驱油效果等方面。
这些计算方法在油藏工程的勘探、开发和生产中具有重要的应用价值,能够帮助工程师和研究人员更好地了解和评估油藏的性质和行为。

低渗透油藏相渗曲线特征规律研究作者:孙永杰来源:《中国化工贸易·中旬刊》2018年第08期摘要:低渗特低渗油田的开发在我国石油生产中占有举足轻重的地位。
研究了太53区块储层的润湿性,对相对渗透率曲线进行了归一化处理,分析相渗曲线特征;认为低渗透储层受储层、流体特征的影响,两相共渗区较窄;随含水饱和度的上升,油相相对渗透率急剧下降,水相相对渗透率上升较快;同时水驱油效率较高。
关键词:低渗透油藏;相对渗透率曲线;归一化;渗流规律相对渗透率曲线是油藏工程研究中的一项重要的基础资料,它反映了油层内天然或人工水驱采油时,油水通过岩石孔隙的流动能力及其渗流阻力的变化规律,是反映一个油藏内部流体渗流特性的基本参数,储层岩石润湿性与相渗曲线的特征值具有一定相关性,油藏相对渗透率曲线等渗点处的含水饱和度大于50%,表现出亲水储层的特征,反之则表现出亲油的特征。
低渗透储层的油水相对渗透率曲线的特征及影响因素,与常规渗透率油藏的相渗曲线存在一定差异,是认识、分析低渗透储層油、水两相渗流机理的重要方法,可以为有效地开发油田提供理论基础。
本文通过室内试验测定了低渗透油藏岩心相对渗透率,分析了其相渗特征。
1 实验基本情况实验岩心取自太29、太43、太47三口井,共3个样本。
实验温度为70℃,采用非稳态法,按SY5345-1999《油水相对渗透率测定方法》测试标准进行。
实验岩芯样品长度为5.82~5.98cm,直径约2.5cm,孔隙度8.04%~12.6%,空气渗透率1.6~13.6×10-3μm2,物性差别不大。
分析3个样品实验数据可以看出,随着岩心渗透率增大,驱油效率、共渗区呈上升趋势,而束缚水、残余油饱和度呈下降趋势,说明试验结果的一致性较好。
2 相渗曲线归一化处理对油水两相相对渗透率的计算,国内水驱砂岩油田广泛采用相关经验公式。
根据测试的油水两相的相对渗透率曲线数据,由线性回归法,得到油田的相渗曲线和含水与饱和度关系曲线。




88随着EBS油田石油资源勘探程度的不断深入、高低渗透储层的稳产状态的已经很难维持。
同时,低渗油藏的注水开发状况复杂,油藏油水分布规律难寻、不同井油水采出程度差异也比较大、再加上储层微观地质条件,水驱油路径与油藏剩余油展布规律认识不清,这都是造成油田增产难以实现的因素。
驱油效率直接影响油气采收率,影响油田的经济效率。
真实砂岩模型驱替实验能直观的发现油藏渗流特征的变化,有更好的科学性,实用性也更强。
同时,EBS在进入含水中期后,开发规律及驱油效率均发生变化,需要对渗流规律进行深入研究,从而指导油田后期的开发。
针对这些问题,本文从储层地质特征出发,结合真实砂岩水驱油实验,对伊拉克东巴油田油层的驱油效率的影响因素进行了分析研究。
一、研究区储层基本特征EBS油田位于巴格达市东北方向14km处,横跨巴格达、迪亚拉、瓦西特三省,占地面积约为658平方公里。
东巴格达油田位于伊拉克Diyala省境内,处于美索不达米亚盆地前渊内,油田面积为1900km2,发现于1976年,1989年投产。
实验最终可采储量4651.38×106bbl,天然气最终可采储量9385000×106ft3。
储集层为Hartha组,其岩性为石灰岩,沉积于浅海相环境,年代为白垩纪坎潘期-马斯特里赫特期,厚度为975ft,平均孔隙度20%;第二储集层为Khasib组,其岩性为石灰岩,沉积环境为浅海相,年代为白垩纪土伦期-康尼亚克期,厚度为300ft,平均渗透率为100mD;第三储集层为Sadi组,其岩性为石灰岩,沉积于深海相环境,年代为白垩纪土伦期-康尼亚克期,厚度为975ft;第四储集层为Tanuma组,其岩性为石灰岩,沉积环境为浅海相,年代为白垩纪土伦期-坎潘期,厚度为250ft,平均孔隙度20%;第五储集层为祖拜尔组,其岩性为砂岩,沉积环境为浅海相环境,年代为白垩纪欧特里夫期-阿普特期早期,厚度为1650ft。
圈闭为构造圈闭,是背斜和断层构造。
计算油田特高含水期相渗曲线新方法王继强;岳圣杰;朱孟高;陈青松;王博【摘要】提出了一种应用油田进入特高含水期后生产动态数据计算油藏相对渗透率的新方法.该方法采用二项式拟合krw/kro与sw的半对数关系曲线,并借助多元线性回归方法,求出油水两相相对渗透率表达式,从而得到相渗曲线.经过与油田开发初期岩心实验测得的相渗曲线对比,发现计算出的相渗曲线能更好地反映出油田长期注水开发后的物性变化,有助于油田特高含水期的地下流体流动的研究.【期刊名称】《石油化工应用》【年(卷),期】2017(036)008【总页数】4页(P62-64,88)【关键词】特高含水;相渗曲线;动态数据;含水饱和度【作者】王继强;岳圣杰;朱孟高;陈青松;王博【作者单位】中国石油勘探开发研究院,北京 100083;中国石油大学(北京),北京102249;胜利油田滨南采油厂,山东滨城 256606;中国石油大学(北京),北京 102249;中国石油大学(北京),北京 102249【正文语种】中文【中图分类】TE312相渗曲线是油田开发中的重要资料,其可用于油田生产的预测[1]。
油田上,相渗曲线的获取主要是来自油田开发初期取心井取出的岩心所进行的岩心实验得到,但由于取心过程中存在钻井液污染和实验条件与地层条件存在差异以及实验误差等因素的影响,岩心实验所获取的相渗曲线并不能完全的反映地下流体的真实流动状态。
尤其是当油田进入到特高含水期时,油层经过长期的注入水冲刷,岩性发生变化,此时用开发初期获取的岩心测得的相渗曲线来预测油田生产动态就会导致一定的偏差[2,3]。
为此,有学者提出用油田动态数据来求出相渗曲线[4-6]。
当前,在我国大多数的油田经过数十年的注水开发,已纷纷进入到“高含水率”、“高采出程度”的双高时期[7,8],为更好地研究这一时期的油田生产情况,改进油田开发方案,就有必要对这一时期的地下流体的流动状态进行研究,本文即是在此情况下提出采用特高含水期的油田开发动态数据来求取相渗曲线,这将有助于更好地指导油田开发方案的调整。
七、油田含水变化规律在油藏注水开发过程中,随着注水工作的不断深入,油井逐渐见水,且含水率将不断升高,含水上升必然影响油田的产量和有关的开发技术政策,给油田开发带来一系列这样或那样的问题,因此研究含水上升规律,根据含水上升规律和特点,控制或延缓含水上升速度,对于保持油田稳产、降低开采成本非常重要。
(一)理论变化分析 1、理论特征3-7-1含水率的变化受多种因素影响,如岩石的润湿性、储层的非均质性、原油性质、油藏类型、注采井网和注采条件等等,因而实际油藏含水率的变化非常复杂,只能进行宏观分析。
⑴油藏类型影响:不同的油藏类型,含水上升规律不同。
底水或边水活跃的油藏,在稳定开采、保持合理采油速度的情况下,无水采油期长、含水上升慢,但油井一旦见水,含水上升就比较快;人工切割注水开发的油藏,因受注采井距大小、油藏非均质性、注水和采油强度等多种因素影响,往往无水采油期短、早期含水上升速度要明显大于底水或边水活跃的油藏。
⑵原油性质不同,含水上升规律不同:多数层状砂岩油藏,因原油性质的差异,油水粘度比不同,含水上升规律表现出不同的特点,一般来说都符合以上所描述的三种模式或者介于它们之间。
⑶含水率与含水上升率的关系:含水率变化规律也就是随着地层中含水饱和度的增加,油井产水率的变化情况。
含水上升率则指每采出1%的地质储量含水率变化的幅度。
判断一个油藏在某一含水阶段开发效果的好坏,通过评价含水上升率指标是油藏开发中常用的方法之一。
通常的做法是应用相对渗透率曲线求得油藏的含水上升率理论曲线,然后与油藏的实际含水上升率比较,如果实际的含水上升率小于理论含水上升率,则认为油藏开发效果好,反之则认为开发效果不理想。
理论含水上升率计算方法如下:根据油田测得的相渗曲线,应用分流量方程计算含水率。
owKw Ko o Ko w Kw w Kw Qo Qw Qw fw μμμμμ⋅+=+=+=11///实际工作中为了便于应用,将油水相对渗透率的比值表示为含水饱和度的函数。
关于油藏的相渗曲线的以及含水饱和度曲线交点求法
小熊维尼
在油藏的期末复习的时候,我就发现了这个问题,明明很正常的fw-Sw曲线,想当然的会以为直接对它求导,然后求得斜率相等的点就行了。
但是往往事与愿违,往往给出的是点的数据,就是测井数据。
那么我们怎么来精确地求得那个交点值呢,以下给出一种数值方法,希望对大家有用。
前期准备:
你必须得有mathematical,matlab或者maple,当然如果你对自己的计算能力有信心,那也行的。
步骤:
1,我们从Excel表格中读取数据(以下我以传姐的数据为例)
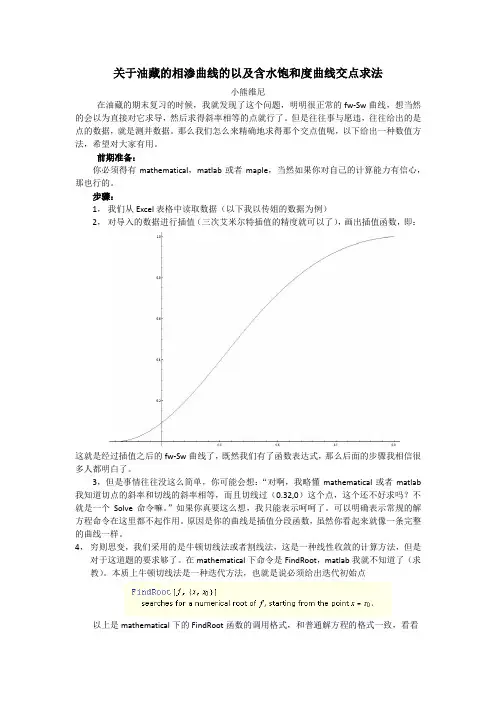
2,对导入的数据进行插值(三次艾米尔特插值的精度就可以了),画出插值函数,即:
这就是经过插值之后的fw-Sw曲线了,既然我们有了函数表达式,那么后面的步骤我相信很多人都明白了。
3,但是事情往往没这么简单,你可能会想:“对啊,我略懂mathematical或者matlab 我知道切点的斜率和切线的斜率相等,而且切线过(0.32,0)这个点,这个还不好求吗?不就是一个Solve命令嘛。
”如果你真要这么想,我只能表示呵呵了。
可以明确表示常规的解方程命令在这里都不起作用。
原因是你的曲线是插值分段函数,虽然你看起来就像一条完整的曲线一样。
4,穷则思变,我们采用的是牛顿切线法或者割线法,这是一种线性收敛的计算方法,但是对于这道题的要求够了。
在mathematical下命令是FindRoot,matlab我就不知道了(求教)。
本质上牛顿切线法是一种迭代方法,也就是说必须给出迭代初始点
以上是mathematical下的FindRoot函数的调用格式,和普通解方程的格式一致,看看
下面的例子就明白了
5,通过这样的方法我们就可以得到交点的x数值了带入插值函数(就是上面的函数可以求得y值了。
这样就可以把切线完美的表达出来了(两个点了)。
如下图:
以下是传姐同学的数据,大家可以先仿照做一遍,看看自己做对没有:。