当前位置：文档之家 › 化学反应工程第四章答案

化学反应工程第四章答案

  • 格式：doc
  • 大小：589.50 KB
  • 文档页数：18

下载文档原格式

  / 18

合集下载

化学反应工程第二版习题解答

化学反应工程第二版习题解答

目 录第一章习题 ............................................................... 错误!未定义书签。

第二章习题 ............................................................... 错误!未定义书签。

第三章习题 ............................................................... 错误!未定义书签。

第四章习题 ............................................................... 错误!未定义书签。

第五章习题 ............................................................... 错误!未定义书签。

第六章习题 ............................................................... 错误!未定义书签。

第七章习题 ............................................................... 错误!未定义书签。

第八章习题 ............................................................... 错误!未定义书签。

第一章习题1 化学反应式与化学计量方程有何异同?化学反应式中计量系数与化学计量方程中的计量系数有何关系?答：化学反应式中计量系数恒为正值，化学计量方程中反应物的计量系数与化学反应式中数值相同，符号相反，对于产物二者相同。

2 何谓基元反应?基元反应的动力学方程中活化能与反应级数的含义是什么?何谓非基元反应?非基元反应的动力学方程中活化能与反应级数含义是什么?答：如果反应物严格按照化学反应式一步直接转化生成产物，该反应是基元反应。

化学反应工程第四章习题答案

化学反应工程第四章习题答案
60停留时间分布密度函数E(t)的含义？
答：在定常态下的连续稳定流动系统中，相对于某瞬间t=0流入反应器内的流体，在反应器出口流
体的质点中，在器内停留了t至U t+dt之间的流体的质点所占的分率为E(t)dt(②分)。
停留时间分布的实验数据来确定所提出的模型中所引入的模型参数;
过模拟计算来预测反应结果；4) 通过一定规模的热模实验来验证模型的准确性。
3||2(t3E(t)3tE(t)5tE(t)7)tE(t)9
3
=vt =0.86.187 =4.95(m)
°02-2
=°t E(t)dt -t
2G
2
= 47.25 -(6.187)=8.971
8.971
2
(6.187)
= 0.234
73. 某反应器用示踪法测其流量，
不可逆反应，此反应若在活塞流反应器中进行，转化率为 出口转化率。
2
◎a解：-
8(丄)2=0.2178
Pe Pe
2
a
= 4.59
XA
活塞流:
dxA
kCA0(1
kt
d(1—Xa)
1
=In4.60
1 -Xa
Xa
=1 -
,ktn
(1 )
N
Xa
=96%
75.用多级全混流串联模型来模拟一管式反应装置中的脉冲实验, 求
1)
2)
已知
2
6=8.971t2=6.187
1)
2)
推算模型参数N;
质的交换，微团内部具有均匀的组成和相同的停留时间，这种流体称为宏观流体。如在气一液鼓泡
搅拌装置中，气体以气泡方式通过装置，此时气体是宏观流体，而液体为微观流体。

化学反应工程习题答案

化学反应工程习题答案

后
答
dcA ，有什么条件? dt
w.
案
网
co
m
1
《化学反应工程》第二版习题解答
A+C↔D 解
2 rA k1cA cB k2cC k3cA cC k4cD 2 rB 2k1cA cB 2k2cC
(1)
rD k3cA cC k4cD
2 rA k1cA cB k2cC 2 rB 2k1cA cB 2k2cC k3cBcC k4cD
p p rA k c c kc A B RT RT
ww
kP
kc 2.65 104 m 6 kmol 2s 1 ( RT )3 8.314kJ kmol1K 1 303K
kh
2
气 相 基 元 反 应 A+2B → 2P 在 30 ℃ 和 常 压 下 的 反 应 速 率 常 数 k c =2.65 × 104m6kmol-2s-1。现以气相分压来表示速率方程，即(−r A )=k P p A p B 2，求k P =? （假定气体为理想气体）
pA
3 pA0 2 pA
答
w.
25℃下测得下列数据，试确定该反应反 913.8 70.6 28.2 1188 65.3 22.9 ∞ 42.4 0 490.2 913.8 1188
5
ww
w.

以
解 由c A -c B =42.4 可知反应应按下列方式A+B→产物进行 设为二级反应
1 c c dcA ln A B0 kcA cB 积分得： kt cA0 cB0 cA0cB dt 1 c ln A 对 t 作图若为直线，则假设正确。 cA0 cB0 cB

化学反应工程分析第四章一二节.

化学反应工程分析第四章一二节.
式中， Da为第二Damköhler数。
（4.6）
• 对一级反应
k kcAb Da kga kga(cAb 0)
• 对n级反应
（4.7）
kcAb n kcAb n1 Da kga(cAb 0) kga
（4.8）
可能的最大反应速率是指可能出现的最高反应物浓度下 得到的反应速率，而可能的最高反应物浓度为cAb，可能的最 大传质速率，是指反应物在催化剂表面浓度为零，传质推动 力最大时的传质速率。 Damkohler数的物理意义即为可能的最大反应速率和最大 传质速率之比。
（4.17）
不同反应级数时ƞeDa和ƞe关系，由式（4.12）和式（4.14） ~（4.16）得到，并以被标绘在图4.3中。
图4.3 不同级数反应的等温外部效率因子和ƞeDa的关系
十分明显，当过程由外扩散控制时，表观速率对于主体浓度呈一 级关系，由传质速率决定，表观活化能很小，可视作接近零。如 为反应控制，则表观动力学与本征动力学一致。
• 效率因子法
Ei - rA k 0ie RTb cAb ni
-
（4.2）
效率因子ƞ用来校正传递过程对反应速率的影响，考虑外 部传递影响的效率因子称为外部效率因子，考虑内部传递 影响的效率因子称为内部效率因子，同时考虑两者影响的 为总效率因子。 • 表观动力学法
Ea - rA k 0ae RTb cAb na
2 3
即：
Pr 式中， ,为Schmidt数，表示物系的扩散特性； 为Prandtl数，表示物系的传热特性。两量纲为一数定义的D 和ƛ 分别为分子扩散系数和导热系数。
Sc
D
h Sc cp ( ) kg Pr
2 3
cp

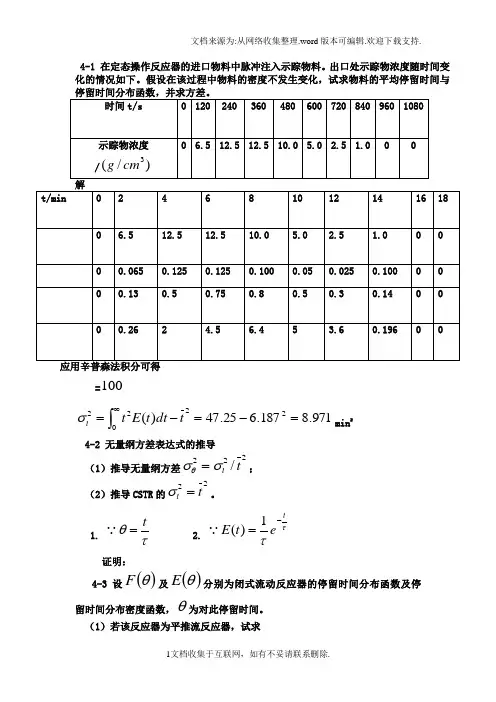
化学反应工程第四章答案

化学反应工程第四章答案

4-1 在定态操作反应器的进口物料中脉冲注入示踪物料。

出口处示踪物浓度随时间变化的情况如下。

假设在该过程中物料的密度不发生变化，试求物料的平均停留时间与=100⎰∞=-=-=02222971.8187.625.47)(t dt t E t tσmin 24-2 无量纲方差表达式的推导 （1）推导无量纲方差222/ttσσθ=；（2）推导CSTR 的22tt=σ。

1. τθt=2. ττtet E -=1)(证明： 4-3 设()θF 及()θE 分别为闭式流动反应器的停留时间分布函数及停留时间分布密度函数，θ为对此停留时间。

（1）若该反应器为平推流反应器，试求①F(1); ②E(1);③F(0.8);④E(0.8);⑤F(1.2) （2）若该反应器为全混流反应器，试求①F(1); ②E(1);③F(0.8);④E(0.8);⑤F(1.2) （3）若该反应器为非理想流动反应器，试求 ①F(∞); ②F(0);③E(∞);④E(0);⑤⎰∞0)(θθd E ；⑥⎰∞)(θθθd E解1平推流模型 2 全混流θθ-=e E )( ， θθ--=e F 1)(3非理想流动模型a 多釜串联 θθθN N N e N N E ---=1)!1()(， 0)(C C F N =θ4-4 C(t)t/min4-18图用阶跃法测定某一闭式流动反应器的停留时间分布，得到离开反应器的示踪剂浓度与时间的关系，如图4-18所示。

试求 （1）该反应器的停留时间分布函数)(θF 及分布密度函数)(θE ；（2）数学期望θ 及方差2θσ；（3）若用多釜串联模型来模拟该反应器，则模型参数是多少？ （4）若用轴向扩散模型来模拟该反应器，则模型参数是多少？（5）若在此反应器内进行1级不可逆反应，反应速率常数1min 1-=k ，且无副反应，试求反应器出口转化率。

解（1）.()()θF c t c t F ==0)(⎪⎩⎪⎨⎧-=12)(t t c 3322〉≤≤≤t t t()⎪⎩⎪⎨⎧-==∴120)(0t c t c t F 3322〉≤≤≤t t t ，()θF t F =)(⎪⎩⎪⎨⎧=∆∆=010)(0t c c t E3322〉≤≤≤t t t ，()t t E E =)(θ（2）.1==-ttθ（3）. 多釜串联模型 (4). 轴向扩散模型 试差 Pe=0.001 (5).4-5. 为了测定某一闭式流动反应器的停留时间分布，采用脉冲输入法，反应（1）反应物料在该反应器中的平均停留时间t 及方差2θσ（2）停留时间小于4.0min 的物料所占的分率。

《化学反应工程》第三版(陈甘堂著)课后习题答案

《化学反应工程》第三版(陈甘堂著)课后习题答案

《化学反应工程》第三版(陈甘堂著)课后习题答案第二章均相反应动力学基础2－4三级气相反应2NO+O22NO2，在30℃及1kgf/cm2下反应，已知反应速率常数2kC=2.65×104L2/(mol2 s)，若以rA=kppApB表示，反应速率常数kp应为何值？解：原速率方程rA=dcA2cB=2.65×104cAdt由气体状态方程有cA=代入式（1）2－5考虑反应A课所以kp=2.65×104×(0.08477×303) 3=1.564后当压力单位为kgf/cm2时，R=0.08477，T=303K。

答p p 2rA=2.65×10 A B =2.65×104(RT) 3pApBRT RTp表示的动力学方程。

解：.因，wwnAp=A，微分得RTVdaw案24网pAp，cB=BRTRT3P，其动力学方程为( rA)=dnAn=kA。

试推导：在恒容下以总压VdtVδA=3 1=21dnA1dpA=VdtRTdt代入原动力学方程整理得wdpA=kpAdt设初始原料为纯A，yA0=1，总量为n0=nA0。

反应过程中总摩尔数根据膨胀因子定义δA=n n0nA0 nA若侵犯了您的版权利益，敬请来信通知我们！Y http://.cn.co（1）mol/[L s (kgf/cm2) 3]m（1）则nA=nA01(n n0)δA1(P P0)δA（2）恒容下上式可转换为pA=P0所以将式（2）和式（3）代入式（1）整理得2－6在700℃及3kgf/cm2恒压下发生下列反应：C4H10发生变化，试求下列各项的变化速率。

（1）乙烯分压；（2）H2的物质的量，mol；（3）丁烷的摩尔分数。

解：P=3kgf/cm2，（1）课MC4H10=58，（2）w.krC2H4=2( rC4H10)=2×2.4=4.8kgf/(cm2 s)PC4H10=PyC4H101 dpC4H10= P dt2.4-1==0.8 s 3w（3）nC4H10=nyC4H10=n0(1+δC4H10yC4H10,0xC4H10)yC4H10dnH2dtdnH2dt=hdaw后n0=nC4H10,0=δC4H10rC4H10=反应开始时，系统中含C4H*****kg，当反应完成50%时，丁烷分压以2.4kgf/(cm2 s)的速率dyC4H10dt答1rCH=2.4224wdnC4H10dt案116×1000=2000mol582+1 1==21网dyC4H10=n0(1+δC4H10yC4H10,0xC4H10) dt=2000×(1+2×1×0.5)×0.8=3200 mol/s若侵犯了您的版权利益，敬请来信通知我们！Y http://.cno2C2H4+H2，dP=k[(δA+1)P0 P]=k(3P0 P)dtm（3）dpA1dP= dtδAdt2－9反应APS，( r1)=k1cA , ( r2)=k2cp，已知t=0时，cA=cA0 ，cp0=cS0=0, k1/k2=0.2。

反应工程答案

反应工程答案

第二章 均向反应动力学1.在473K 等温及常压下进行气相反应：（1）3→A R 1.5R A r C = （2）2→A S0.5S Ar C =（3）→A T 2.1TA r C= 式中C A 为反应物A 的浓度（kmol/l ），原料中A 和惰性气体各为一半（体积比），试求当A 的转化率达85%时，其转化速率是多少？解：先求出总摩尔变化数δA ，首先将产物的生成速率变为对应的反应物的转化速率：10.53AR R A r r C ==10.252AS S A r r C == 2.1AT T A r r C== 总反应速率为： 2.85A AR AS AT AR r r r C =++= 以一摩尔反应物A 为基准，总摩尔变化数为：0.50.25 2.13210.4392.85 2.85 2.85A δ=⨯+⨯+-=初始浓度为：200030.10130.5 1.28810/8.31410473A A P y C kmol l RT --⨯===⨯⨯⨯则有：2300(1) 1.288100.151.62810/110.50.4390.85A A A A A A C X C kmol ly X δ---⨯⨯===⨯++⨯⨯332.85 2.85 1.62810 4.64010/(.min)A A R C kmol l --==⨯⨯=⨯2.可逆一级液相反应PA −−←−→−，已知0,m kmol 5.0P030=⋅=-c c A ；当此反应在间歇反应器中进行，经过8min 后，A 的转化率为33.3%，而平衡转化率是66.7%，求此反应的动力学方程式。

解：()()x c k x c k txc t c x c c x c c c c k c k c k c k tc r A02A01A0A A0P A0A A A02A 1P 2A 1AA 1d d d d )1(d d --==-=-=--=-=-=-⎩⎨⎧=====+-+-=xx t t x t txk k k xx k k k tx,0,0d )(d )(d d 2112118333.022667.01667.01)1()(ln 121e e e 0A e 0A Ae Pe 21121121=====-=-=-====+-+-t x k k K x x x c x c c c k k K t k xk k k k k ()PA A A 1211212121212102888.005776.0d d min02888.0min 05776.02/08664.086931.05.0ln 18333.02111ln 1c c tcr k k k k k k k k k k k k -=-=-⎩⎨⎧==⎩⎨⎧==+=+=+-=⎪⎪⎭⎫ ⎝⎛⨯⎪⎭⎫ ⎝⎛+-+--- 3.液相自催化反应的动力学方程A+P-P+P 速率表达式00()/(.) c 0.95/ c 0.05/AA A P A P dc r kc c mol l h mol L mol L dt -=-===，1h 后测得速率最大值，求反应速率常数。

化学反应工程知到章节答案智慧树2023年天津大学

化学反应工程知到章节答案智慧树2023年天津大学

化学反应工程知到章节测试答案智慧树2023年最新天津大学第一章测试1.碳球在空气中燃烧生成二氧化碳，初始的碳和氧气的摩尔比为1：2，初始的碳球直径为5mm，随着反应的进行，碳球直径变为1mm。

请问此时气相的总摩尔数是：参考答案:不变的2.碳球在空气中燃烧生成一氧化碳，初始的碳和氧气的摩尔比为1：1，初始的碳球直径为5mm，随着反应的进行，碳球直径变为1mm。

请问此时气相的总摩尔数是：参考答案:增加的3.碳球在空气中燃烧生成二氧化碳，初始的碳和氧气的摩尔比为1：1，初始的碳球直径为5mm，随着反应的进行，碳球直径变为1mm。

请问此时碳的转化率与氧气的转化率：参考答案:相等4.碳球在空气中燃烧生成一氧化碳，初始的碳和氧气的摩尔比为1：0.5，初始的碳球直径为5mm，随着反应的进行，碳球直径变为1mm。

请问此时碳的转化率与氧气的转化率：参考答案:相等5.碳球在空气中燃烧首先生成一氧化碳，随后深度氧化成二氧化碳，初始的碳和氧气的摩尔比为1：1，初始的碳球直径为5mm，随着反应的进行，碳球直径变为1mm。

两步反应的反应进度：参考答案:只有当两种碳氧化物的生成量相同时才相等;两步反应有各自的反应进度第二章测试1.反应速率定量描述了反应器中某一点的反应快慢。

参考答案:对2.当多个反应同时发生时，只有一个相对反应速率，即。

参考答案:错误;各步反应有各自的相对反应速率3.非基元反应的化学计量系数可以同时乘或除以非零的数，基元反应也同样。

参考答案:仅对非基元反应的描述正确;错误;仅对基元反应的描述错误4.对气相反应因其总摩尔数发生变化，所以CO2的浓度由下式计算：参考答案:错误5.反应速率方程中的摩尔浓度可以替换成摩尔数或反应体积。

参考答案:错第三章测试1.参考答案:2.参考答案:越小3.判断正误：在间歇釜式反应器中进行的反应，达到一定转化率所需反应时间与反应原料的初始浓度无关。

（）参考答案:错4.在绝热的理想连续釜式反应器中进行某放热反应，关于反应器中温度分布描述正确的是（）参考答案:反应温度高于进料温度;反应釜内的温度均一5.C点;A点第四章测试1.参考答案:1台PFR2.判断正误：相同的原料及温度条件下，在由两台反应体积均为1m3的串联活塞反应器（工况1）和一台反应体积为2 m3的活塞流反应器（工况2）中，分别进行反应A→P。

化学反应工程第四章

化学反应工程第四章

E t dt 1
0

N 即： N 1
流体进口 出口
系统
4.2 停留时间分布的数学描述（1）
在连续操作的反应器内，如果在某一瞬间（t=0）极快地向入口物流中加入 100个红色粒子，同时在系统的出口处记下不同时间间隔流出的红色粒子数， 结果如下表。
停留时间范 围 t→t+△t 出口流中的 红色粒子数 分率△N/N 0-2 2-3 3-4 4-5 5-6 6-7 7-8 8-9 9-10 10-11 11-12 12-14
停留时间分布密度与分布函数之间的关系
E t
4.2 停留时间分布的数学描述（8）
停留时间 t
停留时间 t
分布函数
分布密度
4.2 停留时间分布的数学描述（9）
2.3 理想流动停留时间分布 一 平推流
停留时间分布函数
0 F(t)= 1 停留时间分布密度 E(t)= 0 t tm t<tm E()= 0 t<tm F()= 1 1 0 <1
对于二级反应，平均转化率
32 k 32 k rA 9k 2
4.4物系聚集状态对化学反应的影响（4）
n>1，微观混合使平均反应速率降低；
n=1，微观混合对平均反应速率无影响；
n<1，微观混合使平均反应速率增大； n=0，微观混合使平均反应速率增大。 对完全离析的反应器： 将每一个物料微团看成一个微型间歇反应器，反应 一定时间后从反应器出口离开。
m=1与全混流模型相同，m=与平推流相同 计算方差：
2 1 E d 0

2


0

0
E d
2 E d

化学工程基础第四章作业答案.doc

化学工程基础第四章作业答案.doc

化学工程基础第四章作业答案第四章化学反应工程的基本原理4-2 在一定条件下，SO2催化制取SO3的反应式为已知反应器入口处SO2的浓度是7.15（摩尔分数，下同），出口物料中含SO2 0.48, 求SO2的转化率。

解∵∴4-3 已知700℃、3´105Pa（绝压）下的反应C4H10 → 2C2H4 H2 （A）（B）反应开始时C4H10为116kg。

求当反应完成50时，cA、pA、yA、cB各为多少解依题意yA,0 1，xA 50 cA,0 37.09kmol·m-3 cA 9.27 kmol·m-3 pA 7.5 ´ 104Pa yA 0.25 kmol·m-3 4-4 乙醇在装有氧化铝催化剂的固定床反应器中脱水，生成乙烯C2H5OH → C2H4 H2O 测得每次投料0.50kg乙醇，可得0.26kg乙烯，剩余0.03kg乙醇未反应。

求乙醇转化率、乙烯的产率和选择性。

解乙醇总消耗量0.50 - 0.03 0.47kg 其转化率xA ´100 94 设生成0.26kg乙烯需乙醇a kg a 0.427kg 乙烯的选择性Sp 0.909 乙烯的收率Yp Sp·xA 0.909 ´0.94 0.854 4-5 在间歇操作搅拌釜中用醋酸和丁醇反应生产醋酸丁酯，反应式为CH3COOH C4H9OH CH3COOC4H9 H2O （A）B （R）（S）已知反应在100℃下进行，动力学方程为-rA 2.9 ´10-7cA2mol·m-3·s-1。

反应物配比为丁醇醋酸＝4.972 1（摩尔比），每天生产醋酸丁酯2400kg（忽略分离损失），辅助生产时间为30min，混合物的密度视为常数。

等于750kg·m-3，试求当醋酸的转化率为50％时所需反应器的体积大小（装料系数取0.7）。

解MA 60 MB 74 MR 116 cA,0 ´750 1.753kmol·m-3 1753 mol·m-3 qn,A,0 1.724 kmol·h-1 1.724 ´103 mol·m-3 qV,0 0.9835m3·h-1 V qV,0tr t/ 0.9835 ´32.78 30 ´ 1.03m3 VR 1.47m3 4-6 某气相一级反应A →3R，反应速度常数k 8.3310-3s-1，在间歇反应器中进行，初始条件为纯A，总压为101325Pa。

化学反应工程 第四版 第四章作业题答案

化学反应工程 第四版 第四章作业题答案

tC
t 0

p
C
t 0

1022.5 s 20.25 s 50.5
p
（2）EZ/μL的值

2 t
t C
2 t 0

p
C
t 0Leabharlann 23962.5 ˆ t 20.252 64.44 s 2 50.5
2
2
t2
t
2 m
0.157
p
EZ 1 2 0.157 0.079 L Pe 2 2
(2) PFR
1 1 x A 1 k 1 0.255.054 71.73% e e
(3)多级串联全混流模型
m 1
2

1 4.505 0.222
m
x Am
1 1 1 kt
, t tm / m
4.505
x Am
1 1 5.054 1 0.25 4.505
92 2.2 1 102 1.5 1 122 0.6 2 1558
ˆ tm t
tC
t 0

p
t
C
t 0
p
t
252.2 5.054 49.9
t2
t 0

t 2C p t
C t
t 0 p

ˆ t2
1558 5.0542 5.679 49.9
p
(2)转化率
按轴向混合模型计算

2 t
t C
2 t 0

p
C
t 0
ˆ t2

陈甘棠主编化学反应工程第四章

陈甘棠主编化学反应工程第四章
第四章 非理想流动
• 上一章讨论了两种不同类型的流动反应 器-CSTR和PFR。在相同的情况下，二者 的操作效果有很大的差别，究其原因是 由于反应物料在反应器内的流动状况不 同，即停留时间分布不同。
平推流反应器，出口的反应物料质点在反应器 内停留了相同的时间。
全混流反应器，出口的反应物料质点具有不 同的停留时间。
在实际反应器中，由于各种工程因素的影响， 流动反应器内物料的流动状况往往偏离平推流 和全混流。
• 对不是平推流的连续操作的反应器，由于 同时进入反应器的物料颗粒在反应器中的 停留时间可能有长有短，因而形成一个分 布，称为“停留时间分布”。这时常常用 平均停留时间来表述，即不管同时进入反 应器的物料颗粒的停留时间是否相同，而 是根据体积流率和反应器容积进行计算
Nt F t N
F t E t dt
0
t
E t t F (t )
t 0
t
E t dt F (t )
t 0
E t
E t dt
F t
t t dt
t
• 自然
F t Et dt
t 0
F Et dt 1
• 讨论的系统为封闭系统： • 系统进口处有进无出，系统出口处有出无进
停留时间分布理论不仅是化学反应工程学 科的重要组成部分，而且还广泛地应用于吸 收、萃取、蒸馏及结晶等分离过程与设备的 模拟。一方面通过测定分布来分析工况、来 检查设备是否存在死区或短路等情况；另一 方面可以建立合适的流动模型，作为物料衡 算、热量衡算等的基础。 • 描述停留时间分布则是根据概率理论中的概 率密度函数和概率函数来描述。 •
停留时间：流体从进入系统时算起，到其离开系统时

化学反应工程课后习题答案

化学反应工程课后习题答案

化学反应工程课后习题答案化学反应工程课后习题答案化学反应工程是化学工程学科中的重要分支之一，它研究的是化学反应在工业生产中的应用。

通过对反应过程的分析和优化，可以提高反应的产率、选择性和经济性。

在学习化学反应工程的过程中，我们经常会遇到一些习题，下面我将为大家提供一些常见习题的解答。

1. 习题一：对于一个一级反应A→B，初始浓度为C0的A，经过一段时间t后，浓度为Ct。

求该反应的速率常数k。

解答：根据一级反应的速率方程，可以得到d[A]/dt = -k[A]，其中d[A]/dt表示A的浓度随时间的变化率。

根据题意，我们可以得到d[A]/dt = (Ct - C0)/t。

将这两个式子相等，可以得到(Ct - C0)/t = -k[A]。

由于初始浓度为C0的A，所以[A] = C0。

将这个值代入上式，可以得到(Ct - C0)/t = -kC0。

整理一下，就可以得到k = (C0 - Ct)/C0t。

2. 习题二：对于一个二级反应A + B→C，初始浓度分别为C0的A和C1的B，经过一段时间t后，浓度分别为Ct的A和Ct+1的B。

求该反应的速率常数k。

解答：根据二级反应的速率方程，可以得到d[A]/dt = -k[A][B]，d[B]/dt = -k[A][B]。

根据题意，我们可以得到d[A]/dt = (Ct - C0)/t，d[B]/dt = (Ct+1 - C1)/t。

将这两个式子相等，可以得到(Ct - C0)/t = (Ct+1 - C1)/t = -k[A][B]。

由于初始浓度分别为C0的A和C1的B，所以[A] = C0，[B] = C1。

将这两个值代入上式，可以得到(Ct - C0)/t = (Ct+1 - C1)/t = -kC0C1。

整理一下，就可以得到k = (C0- Ct)/(C0C1t) = (Ct+1 - C1)/(C0C1t)。

3. 习题三：对于一个零级反应，初始浓度为C0的A，经过一段时间t后，浓度为Ct。

化学反应工程 第四章

化学反应工程 第四章
V V 'RA V 'RB
在t时对出口处的示踪物B作物料衡算：
所以，
VC V 'RA 0 V 'RB C0
C V 'RB C0 V
＝停留时间≤t的示踪物溶液体积所占分率最后得：F(t)(
C C0
)
s
3.脉冲法
1）实验步骤
（1）物料保持稳定流动
（2）在一瞬间注入示踪剂B，总量是M，在体积流量V中的
t tm＝t
则
2 t
t2E(t)dt
2
t
0
0
对离散型测定值，
t2E(t)
2 t
0
tm2
E(t)
0
三、对比时间 为了方便起见，常用对比时间作为变量。 对比时间的定义
t
tm
1.平均对比停留时间
tm 1
tm
2. E( )
3. F ( )
E( )
dF ( ) d
dF ( )
d( t )
浓度为Co 。数学描述为 0 t 0
C C0 0 t t0
0 t t0
c(∞)
C0
C(t)
t0
V ( M )Ccp(t)
0
0
t=0
t
（３）以t＝0为计时基准，检测出口处的B浓度C。
响应t 曲线 t
（４）标绘
V
( M
)C p
~
t
曲线
２）( V
M
)Cp
?
在出口处作示踪物B的物料衡算：
V C dt Mt
在实际 反应器中，物料可能是由固体颗粒、液滴、气泡或者 分子团块等聚集体组成的，称之为微团。微团之间的混合程度 有三种情况，

化工反应工程答案 第四章

化工反应工程答案 第四章

4 管式反应器4.1在常压及800℃等温下在活塞流反应器中进行下列气相均相反应：6532664+→+C H CH H C H CH在反应条件下该反应的速率方程为：0.51.5,/.=T H r C C mol l s式中C T 及C H 分别为甲苯及氢的浓度，mol/l ，原料处理量为2kmol/h ，其中甲苯与氢的摩尔比等于1。

若反应器的直径为50mm ，试计算甲苯最终转化率为95%时的反应器长度。

解：根据题意可知甲苯加氢反应为恒容过程，原料甲苯与氢的摩尔比等于1，即：00=T H C C ，则有：0(1)==-T H T T C C C X示中下标T 和H 分别代表甲苯与氢，其中：53300330000.5 1.01310 5.6810/8.3141010732/21/0.27810/--⨯⨯===⨯⨯⨯====⨯T T T T p C kmol mRT F Q C kmol h kmol s所以，所需反应器体积为：00000.5 1.500 2.50.95333 1.5 1.501.5 1.5(10.95)10.278100.4329 3.0061.5(5.6810)(1) 1.51---==--=⨯=⨯=⨯--⎰⎰⎰TT X X T Tr T T T H T T T dX dX V Q C Q C C C C dX mX 所以，反应器的长度为：23.0061531.10.05 3.14/4=⨯m4.2根据习题3.2所规定的条件和给定数据，改用活塞流反应器生产乙二醇，试计算所需的反应体积，并与间歇釜式反应器进行比较。

解：题给条件说明该反应为液相反应，可视为恒容过程，在习题 3.2中已算出：0275.8/=Q l h 0 1.231/=A C mol l所以，所需反应器体积：00000000(1)()275.80.95818.61 5.2 1.23110.95=--===-⨯-⎰AX Ar A A A B A A A A A dX V Q C kC X C C X Q X lkC X由计算结果可知，活塞流反应器的反应体积小，间歇釜式反应器的反应体积大，这是由于间歇式反应器有辅助时间造成的。

化学反应工程第4章

化学反应工程第4章

7
四、停留时间分布
• 停留时间分布（简称RTD）:由于反应器中物 停留时间分布（简称 ） 由于反应器中物 料的返混， 料的返混，造成了所有流体微元的停留时间 有长有短，呈现了一种概率分布。 有长有短，呈现了一种概率分布。即返混造 成了停留时间分布。但并非只有返混才可以 成了停留时间分布。 引起停留时间分布。 层流：无返混， 引起停留时间分布。如：层流：无返混，但 却存在着停留时间分布。 却存在着停留时间分布。 • 由此可知，返混与停留时间分布并无确定的 由此可知，返混与停留时间分布并无确定的 一一对应关系， 一一对应关系，一定的返混必然形成确定的 停留时间分布， 停留时间分布，但是一定的停留时间分布并 不一定由确定的返混引起的。 不一定由确定的返混引起的。
18
∞
= ∑(t − t)2 E(t)∆t
统计量的物理意义: 统计量的物理意义: 数学期望：代表均值（统计量的平均值）， 数学期望：代表均值（统计量的平均值）， 这里是平均停留时间。 这里是平均停留时间。 代表统计量的分散程度， 方 差：代表统计量的分散程度，这里 是停留时间对均值的偏离程度。 是停留时间对均值的偏离程度。
5
6
三、按返混程度对反应器的分类
1.完全不返混型反应器 完全不返混型反应器 • 2.充分返混型反应器 充分返混型反应器 • 3.部分返混型反应器 部分返混型反应器 •在这类反应器中物料之间存在一定程度的 在这类反应器中物料之间存在一定程度的 返混，但并未达到充分返混的程度， 返混 ， 但并未达到充分返混的程度 ， 现将 这类反应器称为非理想流动反应器。 这类反应器称为非理想流动反应器。
26
27
c/c0 1 阶跃输入前进入的物料 阶跃输入后进入的物料 t=0 响应曲线 t
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

4-1 在定态操作反应器的进口物料中脉冲注入示踪物料。

出口处示踪物浓度随时间变化的情况如下。

假设在该过程中物料的密度不发生变化，试求物料的平均停留时间与时间t/s 0 120 240 360 480 600 720 840 960 1080示踪物浓度/)/(3cm g 0 0 0t/min246810121416 183/cm g c i0 0 0min/1)(it E0 0 0i i t E t )( 00 0min)(2i it E t0 2 5 0 0])(2)(4[3109753864210c c c c c c c c c c tdt c i +++++++++∆=⎰∞]0)5.20.1025.1(2)0.10.55.125.6(40[32++++++++= =100min)/1(100)()(0tii c dt c t c t E ==⎰∞})(])()()()([2])()()()([4)({31010997755338866442211_t E t t E t t E t t E t t E t t E t t E t t E t t E t t E t tt +++++++++∆=]0)03.08.05.0(2)14.05.075.013.0(40[32+++++++++=min 187.6=⎰∞=-=-=02222971.8187.625.47)(t dt t E t tσmin 24-2 无量纲方差表达式的推导 （1）推导无量纲方差222/ttσσθ=；（2）推导CSTR 的22tt=σ。

1. τθt=2. ττtet E -=1)(证明：2022)(ii i ittt t E t -∆=∑∞σ ⎰∞--=221tdt e t t ττ22)()()()(ττθθττθ--=⎰∞-d t E()]1)1([022--=⎰∞θθθτd E22θστ= 222/τσσθt=∴ 220222)(1)(--∞-=-=⎰⎰t dt e tt dt t E t ttττσ222ττ-=2τ=22τσ=t4-3 设()θF 及()θE 分别为闭式流动反应器的停留时间分布函数及停留时间分布密度函数，θ为对此停留时间。

（1）若该反应器为平推流反应器，试求 ①F(1); ②E(1);③F;④E;⑤F（2）若该反应器为全混流反应器，试求 ①F(1); ②E(1);③F;④E;⑤F（3）若该反应器为非理想流动反应器，试求 ①F(∞); ②F(0);③E(∞);④E(0);⑤⎰∞0)(θθd E ；⑥⎰∞)(θθθd E解1平推流模型0)(=θF )(t t 〈 0)(=θE )(t t ≠ 1)(=θF )(t t ≥ ∞=)(θE )(t t =)()(τθtF F =⎪⎩⎪⎨⎧===2.1,18.0,01,1θθθ⎩⎨⎧=====8.0,01,1)()(θθτθt E E2 全混流θθ-=e E )( ， θθ--=e F 1)(==)()(τθt f F ⎪⎭⎪⎬⎫=-=-=----699.01551.01632.012.18.01e e e ⎪⎩⎪⎨⎧===2.18.01θθθ==)()(τθtE E ⎪⎭⎪⎬⎫==--449.0368.08.01e e ⎩⎨⎧==8.01θθ3非理想流动模型a 多釜串联 θθθN N N e N N E ---=1)!1()(， 0)(C C F N =θ()()1]!11)(!21)(!111[1)(12=-++++-=∞--N N N N N N e F θθθθ()()0]!11)(!21)(!111[1)0(12=-++++-=--N N N N N N eF θθθθ()()()0!11=-=∞--θθN N Ne N N E()()1,00!1001≠=-=-N e N N E N N()()1!1!1)(01010=-=-=⎰⎰⎰∞--∞--∞θθθθθθθθd e N N d e N N d E N N NN N N ()1!1)(0=-=⎰⎰∞-∞θθθθθθd e N N d E N N N4-4 C(t)00.20.40.60.811.2012345系列1t/min4-18图用阶跃法测定某一闭式流动反应器的停留时间分布，得到离开反应器的示踪剂浓度与时间的关系，如图4-18所示。

⎪⎩⎪⎨⎧-=120)(t t c 3322〉≤≤≤t t t试求 （1）该反应器的停留时间分布函数)(θF 及分布密度函数)(θE ；（2）数学期望θ 及方差2θσ；（3）若用多釜串联模型来模拟该反应器，则模型参数是多少？ （4）若用轴向扩散模型来模拟该反应器，则模型参数是多少？（5）若在此反应器内进行1级不可逆反应，反应速率常数1min 1-=k ，且无副反应，试求反应器出口转化率。

解（1）.()()θF c t c t F ==0)(⎪⎩⎪⎨⎧-=12)(t t c 3322〉≤≤≤t t t()⎪⎩⎪⎨⎧-==∴120)(0t c t c t F 3322〉≤≤≤t t t ，()θF t F =)(⎪⎩⎪⎨⎧=∆∆=010)(0t c c t E3322〉≤≤≤t t t ，()t t E E =)(θ()⎰⎰⎰⎰==⋅++⋅==∞∞2233225232100t dt t tdt dt t dt t tE t()⎪⎪⎩⎪⎪⎨⎧=0250θE 3322〉≤≤≤t t t（2）. 1==-ttθ()751]425[254425]010[25432232322202222222=-=-+⨯+=-==⎰⎰⎰⎰⎰∞-∞-dt t dt t dt t dt t tt dt t E t tt σσθ（3）. 多釜串联模型75122222====θσσστt t t N ()()()θθθθθ75175751!17575!1-----=-=e e N N E N N N()()]!11)(!21)(!111[1)(12---++++-=N N N N N N e F θθθθθ ()()]75!1751)75(!21)75(!111[1)(175275---++++-=θθθθθ e F(4). 轴向扩散模型()0133.075112222==--=-Pee Pe Pe θσ 试差 Pe=(5).()⎰⎰⎰⎰∞---∞-++==-33220101dte dt e dt edt t E e x kt ktktkt A0855.023=-=-te%45.91=A x4-5. 为了测定某一闭式流动反应器的停留时间分布，采用脉冲输入法，反应t/min 0 1 2 3 4 5 6 7 8 9 10()()3//cm g t c0 3 5 6 6 3 2 1 0（1）反应物料在该反应器中的平均停留时间t 及方差2θσ（2）停留时间小于的物料所占的分率。

解t(min) 0 1 2 3 4 5 6 7 8 9 10(3/cm g c i)0 0 3 5 6 6 3 2 1 0()it E0 0()i i t E t0 0 0．528 0．297 0()ii t E t 20 0 0．392 3．168 4．95 5．328 4．802 4．224 2,673 0（1）.])(2)(4[3109753864210c c c c c c c c c c tdt c i +++++++++∆=⎰∞()()025.46321365040[31++++++++++=33.30=33.30)()(0tiic dt c t c t E ==⎰∞ min 1 })(])()()()([2])()()()([4)({31111997755338866442211_t E t t E t t E t t E t t E t t E t t E t t E t t E t t E t tt +++++++++∆=()088.4]0528.089.0792.0196.02297.0686.099.0492.0040[31=+⎪⎪⎭⎫⎝⎛+++++++++=⎰∞=-=-=0222253.10088.4244.27)(t dt t E t tσ63.0222==tt σσθ（2）. ()()()()()()24]321[2014E E E E E dt t E ++++⨯=⎰361.0=4-6将一定量的示踪剂从一管式流动反应器的进口处注入，并在该反应器的出口处连续检测示踪剂的浓度()t c ，得到如下数据：t/min48121620242832())/(/3cm kg t c（1）试根据上述实验数据计算平均停留时间；（2）如果在该管式反应器中进行一级不可逆反应RA k −→−1，11m in 045.0-=k 试计算反应物A 的平均转化率；（3）试根据理想平推流模型计算平均转化率并与（2）结果进行比较；（4）若按照多级CSTR 模型处理，求模型参数N 和停留时间分布函数F(t)。

t min0 481216202428 323/m kg c i0 3 5 5 4 2 1 0 0()it E 0 0 0()ii t E t0 0 0()iit E t 24 9 10 0 0()itt E e045.0-0 0 0（1）. 应用辛普森法则()800=⎰∞dt t c ， ()()80t c t E i =1/min})(])()()([2])()()()([4)({3997755338866442211_t E t t E t t E t t E t t E t t E t t E t t E t t E t tt ++++++++∆= min 73.11=()8.360222=-=⎰∞t dt t E t ii tσ （2）.R A k −→−111m in 045.0-=k()6.0415.010=⨯==-⎰∞-dt t E e x ktA ， %40=A x（3）.平推流%7.99997.01173.11045.0==-=-=⨯--e e x kt A，返混造成了实际转化率下降了50多。

（4）多级CSTR 串联模型47.38.3673.11222≈===-t t N σ ()324332841[1θθθθθ+++-=-eF ， -=tt θθ()θF 01()()θF t F =4-7. 用阶跃法测定某一闭式流动反应器的停留时间分布，得到离开反应器的示t/s0 1525354555657590100()()3//cm g t c（1）试求该反应器的停留时间分布函数及平均停留时间；（2）若在该反应器内的物料为微观流体，且进行1级不可逆反应，反应速率常数105.0-=s k，预计反应器出口出的转化率；（3）若在该反应器内的物料为宏观流体，其他条件不变，试问反应器出口处的转化率是多少?解. （1） ()()0c t c t F = ， ()()tt F t E ∆∆=∴ts0 152535455565759010()3/cm g t c 0()t F0 1 1()310⨯t E0 4 7 13 52 19 13 7 6 0()305.010⨯-itt E e0 0()()∑⎰∞∞∆==iiitt E t dt t tE t()S 2.620151069010107751010136510101955101052451010133510107251510415033333333=+⨯⨯⨯+⨯⨯⨯+⨯⨯⨯+⨯⨯⨯+⨯⨯⨯+⨯⨯⨯+⨯⨯⨯+⨯⨯⨯+=--------（2）. 微观()()∑⎰∆≈=--∞-nii kt kt A t t E e dt t E e x i 01%4.86,136.0100136.0=-=⨯=A x（3）. 宏观，对于一级反应宏观流体与微观流体转化率一样%4.86=Ax4-8.已知一等温闭式流动反应器的停留时间分布密度函数()t te t E 416-=min-1试求：（1）平均停留时间；（2）空时；（3）空速；（4）停留时间小于1min 的物料所占得分率；（5）停留时间大于1min 的物料所占的分率；（6）若用CSTR 串联模型来模拟反应器，则模型参数（N ）为多少？ 解. （1） ()t te t E416-=()21281604040420=====⎰⎰⎰⎰∞-∞-∞-∞dt e tdedt e t dt t tE t tttmin（2）. 空时21==-t τmin （3）. 空速 21==τSmin-1（4）. ()4441141101416-----=-===⎰⎰⎰e edt e dt te dt t E ttt9817.0=（5）. ()0183.0110=-⎰dt t E（6）. CSTR 串联模型参数为：()8323612160404042430222=====-=⎰⎰⎰⎰⎰∞-∞-∞-∞-∞-dt e dtt e det dt e t t dt t E t t t tttσ328321,1222222=⎪⎭⎫ ⎝⎛====--t t t N N tσσσθ4-9 在一个全混釜中，等温下进行零级反应A →B ，反应速率为()L mol r A •=m in /9，进料浓度L mol c A /100=，流体在反应器内的平均停留时间min 1=t，请按下列情况分别计算反应器出口转化率：（1）若反应物料为微观流体； （2）若反应物料为宏观流体; 解. A →B L mol r A•=m in /9， L mol c A /100= min 1=t（1）.微观流体91010AfAfAfA c r c c t -=⇒-=， L mol c Af/1=%90=Afx（2）宏观流体，零级反应，反应速率与浓度无关，kt c c A A =-0()Lmol t k C dt t E kt C dt t E c c A A A A /1910)()(000--=-=-==-∞∞⎰⎰ 90.0=Ax ，与微观流体转化效果相同4-10 在具有如下停留时间分布的反应器，等温进行一级不可逆反应A →P ，反应速率常数为1min2-。