当前位置：文档之家 › 投影误差公式

投影误差公式

  • 格式：ppt
  • 大小：4.40 MB
  • 文档页数：68

下载文档原格式

  / 68

合集下载

投影计算公式

投影计算公式

投影计算公式往往表达方式不止一种，有时很难分辨谁对谁错，我只把“墨卡托投影”、“高斯-克吕格投影”、“UTM投影”、“兰勃特等角投影” （1:100万地形图规范中称作正轴等角圆锥投影，GB/T 14512-93）的正反转换公式列出，因为我基本能保证这些公式的正确性。

“海洋地质制图常用地图投影系列小程序已升级，原下载者请注意下载更新版本。

1．约定本文中所列的转换公式都基于椭球体a -- 椭球体长半轴b -- 椭球体短半轴f -- 扁率e -- 第一偏心率e’ -- 第二偏心率N -- 卯酉圈曲率半径R -- 子午圈曲率半径B -- 纬度，L -- 经度，单位弧度(RAD)-- 纵直角坐标, -- 横直角坐标，单位米(M)2．椭球体参数我国常用的3个椭球体参数如下（源自“全球定位系统测量规范 GB/T18314-2001”）：需要说明的是，在“海洋地质制图常用地图投影系列小程序”中，程序界面上的所谓“北京1954“西安1980”及“WGS 84”在实际计算中只涉及了相应的椭球体参数。

3．墨卡托(Mercator)投影3.1 墨卡托投影简介墨卡托(Mercator)投影，是一种"等角正切圆柱投影”，荷兰地图学家墨卡托（Gerhardus Mercator 1512－1594）在1569年拟定, 假设地球被围在一中空的圆柱里，其标准纬线与圆柱相切接触，然后再假想地球中心有一盏灯，把球面上的图形投影到圆柱体上，再把圆柱体展开，这就是一幅选定标准纬线上的“墨卡托投影”绘制出的地图。

墨卡托投影没有角度变形，由每一点向各方向的长度比相等，它的经纬线都是平行直线，且相交成直角，经线间隔相等，纬线间隔从标准纬线向两极逐渐增大。

墨卡托投影的地图上长度和面积变形明显，但标准纬线无变形，从标准纬线向两极变形逐渐增大，但因为它具有各个方向均等扩大的特性，保持了方向和相互位置关系的正确。

在地图上保持方向和角度的正确是墨卡托投影的优点，墨卡托投影地图常用作航海图和航空图，如果循着墨卡托投影图上两点间的直线航行，方向不变可以一直到达目的地，因此它对船舰在航行中定位、确定航向都具有有利条件，给航海者带来很大方便。

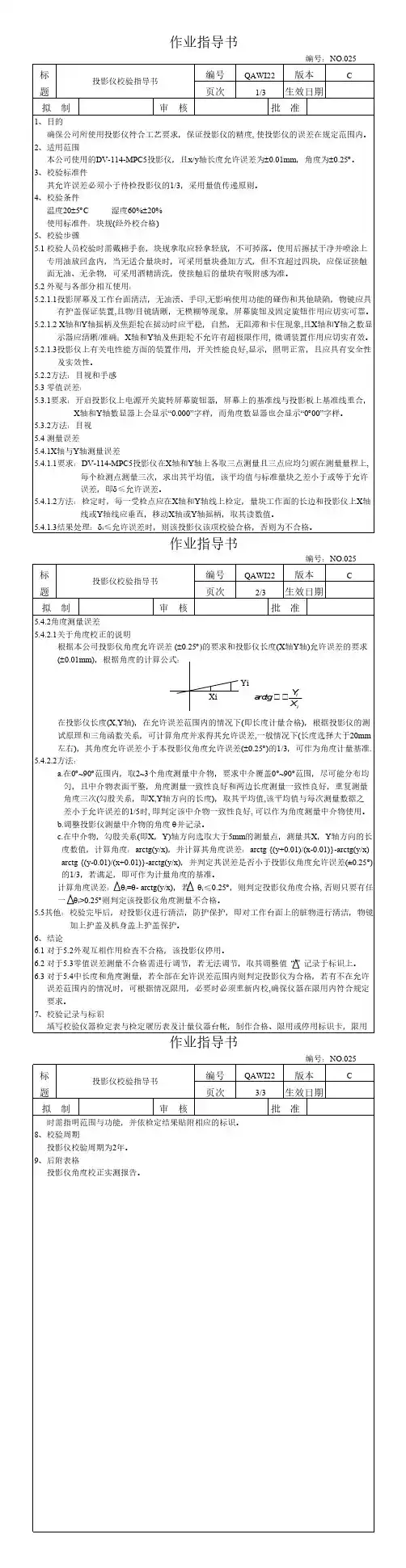
投影仪校验作业指导书

投影仪校验作业指导书

作业指导书 编号：NO.025标投影仪校验指导书编号QAWI22版本C 题页次 1/3生效日期拟 制审 核 批 准1、目的 确保公司所使用投影仪符合工艺要求，保证投影仪的精度,使投影仪的误差在规定范围内。

2、适用范围 本公司使用的DV-114-MPC5投影仪，且x/y 轴长度允许误差为±0.01mm ，角度为±0.25°。

3、校验标准件其允许误差必须小于待检投影仪的1/3，采用量值传递原则。

4、校验条件温度20±5°C 湿度60%±20%使用标准件：块规(经外校合格)5、校验步骤5.1 校验人员校验时需戴棉手套，块规拿取应轻拿轻放，不可掉落。

使用后擦拭干净并喷涂上 专用油放回盒内，当无适合量块时，可采用量块叠加方式，但不宜超过四块，应保证接触 面无油、无杂物，可采用酒精清洗，使接触后的量块有吸附感为准。

5.2 外观与各部分相互使用：5.2.1.1投影屏幕及工作台面清洁，无油渍、手印,无影响使用功能的碰伤和其他缺陷，物镜应具 有护盖保证装置,且物/目镜清晰，无模糊等现象，屏幕旋钮及固定旋钮作用应切实可靠。

5.2.1.2 X 轴和Y 轴摇柄及焦距轮在摇动时应平稳，自然，无阻滞和卡住现象,且X 轴和Y 轴之数显 示器应清晰/准确；X 轴和Y 轴及焦距轮不允许有超极限作用, 微调装置作用应切实有效。

5.2.1.3投影仪上有关电性能方面的装置作用，开关性能良好,显示，照明正常，且应具有安全性 及实效性。

5.2.2方法：目视和手感5.3 零值误差：5.3.1要求：开启投影仪上电源开关旋转屏幕旋钮器，屏幕上的基准线与投影板上基准线重合， X 轴和Y 轴数显器上会显示“0.000”字样，而角度数显器也会显示“0°00”字样。

5.3.2方法：目视5.4 测量误差5.4.1X 轴与Y 轴测量误差5.4.1.1要求：DV-114-MPC5投影仪在X 轴和Y 轴上各取三点测量且三点应均匀颁在测量量程上,每个检测点测量三次，求出其平均值，该平均值与标准量块之差小于或等于允许误差，即d ≤允许误差。

(新版)数值天气预报第二章

(新版)数值天气预报第二章

2
cos 1 sin
cos l le 1 sin
（2.8）式中：l e
(2.8)
a 6371km
2 3 a 11888.45
2
le 为极射赤面投影映像平面上赤道到北极点的距离。
因此，由（2.8）式可以解出 sin
© 2004 By Default
cos l le 1 sin
三 极射赤面投影
极射赤面投影：一种正形割投 影，其投影光源在南极，其映 像面是一个与地球表面北纬 60°相割的平面，即标准纬度 0 600 用这种投影制成的地图， 其经线是一组由北极点向赤道 辐射的直线。而纬线是一组以 北极点为圆心的同心圆。由于 这种投影图在高纬地区的变形 比较小，所以多用作极地天气 图或北半球天气图的底图。 1. k 、l 和 m的表达式


(2.6)
根据(2.4)式有：
极射赤面投影下地图放大系数仅是纬度的函数
kl kl 1 2 3 a cos 2 3 1 m a sin a cos 2a cos 1 sin 2 1 sin




(2.7)
© 2004 By Default
2.实际计算地图放大系数的方法
© 2004 By Default
四 兰勃特投影
兰勃特投影：一种正形圆锥割 投影，其投影光源位于地球球 心，其映像面是一个与地球表 面北纬30°N和60°N相割的圆 锥面，圆锥角为 90 标准纬 度有两个，分别为 1 30 和 2 60 因此又被称为双标 准纬线等角圆锥投影。如图3.8 所示。
地图上任意纬度的距离 映像平面上相应的距离
又称地图比例尺
（3）实际比例尺：
地球曲率公式

地球曲率公式

14
二、像片的投影误差
因地形起伏引起的像点移位——投影误差 1、定义 任一地面点的像点与该地面点在起始（基准） 面上的垂直投影点的像点之间的直线移位。记为 h 由于它是中心投影与垂直投影二种投影方式在 地形起伏情况下产生的差别，故称投影误差，也称 高程位移。 因为底点是铅垂线的合点，所以投影误差位于 底点辐射线上。
投影误差
f A0 B H
h
(n)o a0 a
S
A0 B h r f
得到因地面起伏引起 的像点Leabharlann 移公式AHh
B A0 ( N )O
17
二、像片的投影误差
2、水平像片的 投影误差
(n)o a0 a
h h r H
r为底点辐射距。
S
A
投影误差公式应用 (计算高差)
H
h
B A0 ( N )O
7
8
一、像片的比例尺
2、摄影基线：航向相邻两个摄影站间的距离
P1
S1
B
P2 S2
E
B:摄影基线
9
一、像片的比例尺
3、摄影比例尺
S
a f P
摄影像片当作水平像片，地面取 平均高程时，这时像片上的一段l 与地面上相应的水平距L之比为 摄影比例尺。
H
1 l f m L H
A E f为摄影机主距，H为航高
13
• 理论上讲，理想像片可以作为地形图直接使用。 但是由于在实际航空摄影时，在中心投影的情况 下，当像片有倾斜，地面有起伏时，便会导致地
面点在航摄像片上构像相对于在理想情况下的构
像，产生了位置的差异，反映为一个地面点在地 面水平的水平像片上的构像与地面有起伏时或倾 斜像片上构像的点位不同，这一差异称为像点位 移。
第06讲-像点位移

第06讲-像点位移


s
y o x
X
R称为旋转矩阵，R为正交矩阵，由三个独立参数确定
复 习 Review
方向余弦的确定
X x x Y R R R y R y Z f f
注意：不同的转角系统计算的旋转矩阵是唯一的。
构像方程
已知：
求：
a 2 ( XA X S ) b2 (YA YS ) c2 ( ZA Z S ) XA，YA，ZA a 3 ( XA X S ) b3 (Y YS ) c3 ( Z Z S ) X ，Y ，Z x，y A A S S S ？ ai，bi，ci f， x0 , y0 6个外方位元素 ： XS , YS , ZS ,,ω,κ,
复 习 Review
1、像点的空间直角坐标旋转变换 2、共线条件方程
复 习 Review
坐标对应关系式
Z z y Y x
X x Y R y Z f a1 R b1 c1 a2 b2 c2 ˆ ˆ ˆ a3 cos Xx cos Xy cos Xz ˆ ˆ ˆ b3 cosYx cosYy cosYz ˆ ˆ ˆ c3 cos Zx cos Zy cos Zz
1 f m H
第三章 摄影测量基础知识
2、航摄像片与地形图的区别
2.1 表示方法和内容不同 地形图：按照成图比例尺所规定的各种符号、注记 和等高线表示地物、地貌； 航片：影像的大小、形状和色调。 地形图：用相应的符号和文字、数字注记表示，如 居民楼的名称、房屋的类型、道路的等级等；这些 在像片上没有直接的表示；
O
T
X
T
衣柜投影面积计算公式

衣柜投影面积计算公式

衣柜投影面积计算公式
对于常见的矩形衣柜，可以使用以下公式来计算投影面积：
投影面积=长度×宽度
这里的长度和宽度指的是衣柜底部在地面上的边长。

对于L形衣柜，可以将其视为两个独立的矩形衣柜，然后分别计算它
们的投影面积，最后将两个面积相加。

对于圆形衣柜，计算投影面积需要使用以下公式：
投影面积=π×半径²
这里的半径是指圆形衣柜底部在地面上的半径。

对于其他特殊形状的衣柜，计算投影面积可能要更加复杂，需要将其
分割为多个矩形或其他形状来进行计算。

在实际计算中，可以使用工具如Excel或计算器来帮助进行测量和计算。

首先，需要测量衣柜的底部尺寸，包括长度和宽度。

如果是圆形衣柜，需要测量其底部的直径。

然后，根据衣柜的形状选择适当的公式进行计算。

最后，将测得的数值代入公式中进行计算，得到投影面积的数值。

需要注意的是，计算投影面积时只考虑衣柜底部在地面上的形状，不
考虑衣柜的高度。

所以计算得到的投影面积并不能完全代表衣柜的实际空
间占用情况。

另外，对于非直线边缘或带有斜面的衣柜，计算得到的投影
面积可能会有一定的误差。

总之，衣柜投影面积可以通过根据衣柜的形状和尺寸选择适当的计算公式来计算。

这个面积可以帮助我们评估和规划衣柜所占用的空间大小，从而更好地布置和利用家居空间。

rmse slam计算方式

rmse slam计算方式

rmse slam计算方式SLAM（SimultaneousLocalizationandMapping，即同时定位与地图构建）是一种通过机器学习和计算机视觉技术，实现机器人自主感知环境并构建环境地图的方法。

在SLAM中，通常需要对机器人的运动状态进行估计，以及对环境的地图进行构建。

为了评估SLAM算法的性能，需要使用一些指标，比如RMSE（Root Mean Square Error，即均方根误差）。

RMSE是用来衡量估计值与真实值之间的误差的一种指标。

在SLAM中，通常使用RMSE来评估机器人的运动状态估计和地图构建的准确性。

具体来说，RMSE可以分别用来评估机器人的位置估计误差和方向估计误差，以及地图点的重投影误差。

对于机器人的位置估计误差和方向估计误差，可以用以下公式计算：RMSE_p = sqrt(1/N * sum((p_est - p_gt)^2))RMSE_a = sqrt(1/N * sum((a_est - a_gt)^2))其中，RMSE_p表示位置估计误差的RMSE值，RMSE_a表示方向估计误差的RMSE值，N表示样本数量，p_est表示机器人位置的估计值，p_gt表示机器人位置的真实值，a_est表示机器人朝向的估计值，a_gt表示机器人朝向的真实值。

对于地图点的重投影误差，可以用以下公式计算：RMSE_r = sqrt(1/N * sum((p_proj - p_gt)^2))其中，RMSE_r表示地图点的重投影误差的RMSE值，p_proj表示地图点在估计的相机坐标系下的投影位置，p_gt表示地图点在真实的相机坐标系下的位置。

综上所述，RMSE是衡量SLAM算法性能的一种常用指标，可以用来评估机器人的运动状态估计和地图构建的准确性。

投影于抵偿高程面上的坐标计算方法及其公式推导

投影于抵偿高程面上的坐标计算方法及其公式推导

投影于抵偿高程面上的坐标计算方法及其公
式推导
在进行投影坐标计算时，需要根据地球椭球体模型和投影的数学原理进行计算。

常见的投影方法包括等角投影、等积体投影、等距离投影等。

以等角投影为例，假设地球椭球体模型为WGS-84椭球体，投影平面为球形子午面。

具体计算步骤如下：
1.确定投影中央经线（标准子午线）为λ0，并假设地球椭球体的半长轴为a，扁率为f。

2.对于给定的地理坐标点（经度λ，纬度φ），首先将其转换为弧度表示。

3.根据等角投影的数学原理，可以推导出投影后的平面坐标x和y 的计算公式：
x = a * (λ - λ0) * cosφ
y = a * ln(tan(π/4 + φ/2) * (a / (2 * Ω)))
其中，Ω = a / √(1 - e² * sin²φ)为子午圈半径。

上述公式是等角投影的具体计算公式，其中涉及了对地理坐标到
投影坐标的转换和基本的三角函数计算。

需要注意的是，不同的投影
方法会有不同的计算公式和参数设置，因此在实际应用中需要根据具
体情况进行选择和计算。

在实际应用中，投影坐标计算不仅涉及到了地理坐标系和投影坐
标系的转换，还需要考虑到误差和精度的控制、投影坐标的变换和逆
变换等问题。

因此，需要根据具体需求和情况进行适当的拓展和补充，以实现准确和高效的坐标计算。

6摄影测量第二章(3).

6摄影测量第二章(3).

2. 像点位移：
中心投影时，当像片倾斜或地面有起伏，导致地面点在航 片上构像与理想像片上构像产生位移，称为像点位移。
二、像片倾斜引起的像点位移（倾斜误差）
1、像平面等角点特性
xc rc cos, yc rc sin
rc xc 2 yc 2
tan yc , tan 0 yc0
xc
xc0
yc xc

yc0 xc0
0
2、像点位移
ca ca0 rc rc0

rc2 f
sin sin
3、像点位移规律
0<φ<180时， δα<0 φ=0，180时，δα=0 180<φ<360时, δα>0 φ=90，270时, δα=max
三、地形起伏引起的像点位移（投影误差）
为简洁令：
x y

f f
a1( X A a3(X A a2 (X A

X S ) b1(YA X S ) b3 (YA X S ) b2 (YA
YS ) c1(Z A Z S )
YS ) YS )

c3 (Z A c2 (Z A
ZS) ZS )
, a22

y Ys
, a23

y Z s
, a24

y

, a25

y

, a26

y


x y

f f
a1 ( X A a3 ( X A a2 (X A
X S ) b1 (YA YS ) c1 (Z A Z S )
3摄影测量基础知识

3摄影测量基础知识


Photogrammetry,2004
Photogrammetry & Remote Sensing-----Survey & Mapping Engineering
y
P S
S
a
a0
f
f
o
c
y0
P0
A
h
x x0
像片倾斜引起像点位移
A0
地形起伏引起像点位移
• 航摄像片只要消除像片倾斜与地形起伏引起的像点位移，就 能将中心投影变换为正射投影。要使这种投影具有成图比例尺
Photogrammetry & Remote Sensing-----Survey & Mapping Engineering
(n)oa0 a S
H
A
h
B A0 ( N )O
Photogrammetry,2004
Photogrammetry & Remote Sensing-----Survey & Mapping Engineering
• 航高：指摄影飞机在摄影瞬间相对于某一水准面 的高度，从该水准面起算向上为正。航高分为相对 航高和绝对航高。
Photogrammetry & Remote Sensing-----Survey & Mapping Engineering
相对航高是指摄影机物镜相对于某一基准面的高度，常称 为摄影航高。它是相对于被摄区域内地面平均高程基准面的 设计航高。
3、倾斜误差性质
➢等比线上的点不存在像片倾斜引起的像点位移； ➢当00 1800, a 0，则rc0 rc ，像点朝向等角点位移； ➢当 1800,a 0 ，则rc0 rc ，像点背向等角点位移； ➢当 90、270,sin 1，即在向径相等的情况下，位 于主纵线上的像点的倾斜误差最大。
各种投影转化的算法公式

各种投影转化的算法公式

各种投影转化的算法公式投影计算公式往往表达方式不止一种，有时很难分辨谁对谁错，我只把“墨卡托投影”、“高斯-克吕格投影”、“UTM投影”、“兰勃特等角投影” （1:100万地形图规范中称作正轴等角圆锥投影，GB/T 14512-93）的正反转换公式列出，因为我基本能保证这些公式的正确性。

1．约定本文中所列的转换公式都基于椭球体a -- 椭球体长半轴b -- 椭球体短半轴f -- 扁率e -- 第一偏心率e’ -- 第二偏心率N -- 卯酉圈曲率半径R -- 子午圈曲率半径B -- 纬度，L -- 经度，单位弧度(RAD)-- 纵直角坐标, -- 横直角坐标，单位米(M)2．椭球体参数我国常用的3个椭球体参数如下（源自“全球定位系统测量规范 GB/T18314-2001”）：需要说明的是，在“海洋地质制图常用地图投影系列小程序”中，程序界面上的所谓“北京1954“西安1980”及“WGS 84”在实际计算中只涉及了相应的椭球体参数。

3．墨卡托(Mercator)投影3.1 墨卡托投影简介墨卡托(Mercator)投影，是一种"等角正切圆柱投影”，荷兰地图学家墨卡托（Gerhardus Mercator 1512－1594）在1569年拟定, 假设地球被围在一中空的圆柱里，其标准纬线与圆柱相切接触，然后再假想地球中心有一盏灯，把球面上的图形投影到圆柱体上，再把圆柱体展开，这就是一幅选定标准纬线上的“墨卡托投影”绘制出的地图。

墨卡托投影没有角度变形，由每一点向各方向的长度比相等，它的经纬线都是平行直线，且相交成直角，经线间隔相等，纬线间隔从标准纬线向两极逐渐增大。

墨卡托投影的地图上长度和面积变形明显，但标准纬线无变形，从标准纬线向两极变形逐渐增大，但因为它具有各个方向均等扩大的特性，保持了方向和相互位置关系的正确。

在地图上保持方向和角度的正确是墨卡托投影的优点，墨卡托投影地图常用作航海图和航空图，如果循着墨卡托投影图上两点间的直线航行，方向不变可以一直到达目的地，因此它对船舰在航行中定位、确定航向都具有有利条件，给航海者带来很大方便。

各种投影转化的算法公式

各种投影转化的算法公式投影计算公式往往表达方式不止一种，有时很难分辨谁对谁错，我只把“墨卡托投影”、“高斯-克吕格投影”、“UTM投影”、“兰勃特等角投影” （1:100万地形图规范中称作正轴等角圆锥投影，GB/T 14512-93）的正反转换公式列出，因为我基本能保证这些公式的正确性。

1．约定本文中所列的转换公式都基于椭球体a -- 椭球体长半轴b -- 椭球体短半轴f -- 扁率e -- 第一偏心率e’ -- 第二偏心率N -- 卯酉圈曲率半径R -- 子午圈曲率半径B -- 纬度，L -- 经度，单位弧度(RAD)-- 纵直角坐标, -- 横直角坐标，单位米(M)2．椭球体参数我国常用的3个椭球体参数如下（源自“全球定位系统测量规范 GB/T18314-2001”）：需要说明的是，在“海洋地质制图常用地图投影系列小程序”中，程序界面上的所谓“北京1954“西安1980”及“WGS 84”在实际计算中只涉及了相应的椭球体参数。

3．墨卡托(Mercator)投影3.1 墨卡托投影简介墨卡托(Mercator)投影，是一种"等角正切圆柱投影”，荷兰地图学家墨卡托（Gerhardus Mercator 1512－1594）在1569年拟定, 假设地球被围在一中空的圆柱里，其标准纬线与圆柱相切接触，然后再假想地球中心有一盏灯，把球面上的图形投影到圆柱体上，再把圆柱体展开，这就是一幅选定标准纬线上的“墨卡托投影”绘制出的地图。

墨卡托投影没有角度变形，由每一点向各方向的长度比相等，它的经纬线都是平行直线，且相交成直角，经线间隔相等，纬线间隔从标准纬线向两极逐渐增大。

墨卡托投影的地图上长度和面积变形明显，但标准纬线无变形，从标准纬线向两极变形逐渐增大，但因为它具有各个方向均等扩大的特性，保持了方向和相互位置关系的正确。

在地图上保持方向和角度的正确是墨卡托投影的优点，墨卡托投影地图常用作航海图和航空图，如果循着墨卡托投影图上两点间的直线航行，方向不变可以一直到达目的地，因此它对船舰在航行中定位、确定航向都具有有利条件，给航海者带来很大方便。

各种投影转化的算法公式

各种投影转化的算法公式投影计算公式往往表达方式不止一种，有时很难分辨谁对谁错，我只把“墨卡托投影”、“高斯-克吕格投影”、“UTM投影”、“兰勃特等角投影” （1:100万地形图规范中称作正轴等角圆锥投影，GB/T 14512-93）的正反转换公式列出，因为我基本能保证这些公式的正确性。

1．约定本文中所列的转换公式都基于椭球体a -- 椭球体长半轴b -- 椭球体短半轴f -- 扁率e -- 第一偏心率e’ -- 第二偏心率N -- 卯酉圈曲率半径R -- 子午圈曲率半径B -- 纬度，L -- 经度，单位弧度(RAD)-- 纵直角坐标, -- 横直角坐标，单位米(M)2．椭球体参数我国常用的3个椭球体参数如下（源自“全球定位系统测量规范 GB/T需要说明的是，在“海洋地质制图常用地图投影系列小程序”中，程序界面上的所谓“北京1954“西安1980”及“WGS 84”在实际计算中只涉及了相应的椭球体参数。

3．墨卡托(Mercator)投影3.1 墨卡托投影简介墨卡托(Mercator)投影，是一种"等角正切圆柱投影”，荷兰地图学家墨卡托（Gerhardus Mercator 1512－1594）在1569年拟定, 假设地球被围在一中空的圆柱里，其标准纬线与圆柱相切接触，然后再假想地球中心有一盏灯，把球面上的图形投影到圆柱体上，再把圆柱体展开，这就是一幅选定标准纬线上的“墨卡托投影”绘制出的地图。

墨卡托投影没有角度变形，由每一点向各方向的长度比相等，它的经纬线都是平行直线，且相交成直角，经线间隔相等，纬线间隔从标准纬线向两极逐渐增大。

墨卡托投影的地图上长度和面积变形明显，但标准纬线无变形，从标准纬线向两极变形逐渐增大，但因为它具有各个方向均等扩大的特性，保持了方向和相互位置关系的正确。

在地图上保持方向和角度的正确是墨卡托投影的优点，墨卡托投影地图常用作航海图和航空图，如果循着墨卡托投影图上两点间的直线航行，方向不变可以一直到达目的地，因此它对船舰在航行中定位、确定航向都具有有利条件，给航海者带来很大方便。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

问题 提出
5
6
RC30 ADS40（Leica/Helava） DMC
7
8
空中摄影就是 从空中一定高度上 摄取地面物体影像 的过程。
9
航摄像片的质量主要包括：
①构像质量: ②几何质量: ③表观质量:
影像的分解力，清晰度。 体现在影像的量测性能方面。 色调正常，反差适中。
航空摄影的飞行质量要求：
问题 提出
13
内 容 安 排
14
投影[Projection]
一个空间点按一定方式在一个平面上的构 像，叫做该空间点的投影。
物点、像点、投射线、像面（承影面）
平行投影[Parallel Projection ]
投射线互相平行的投影，叫做平行投影。
正射投影（垂直投影）
局部范围内，地形图可视为地面的垂直投影。
29
向量表达式
z y x S
SA λ Sa
-f
y
xA yA zA x y f
x
a
o
y
A
zA
xA
x f y f
xA zA yA zA
（1）
30
坐标变换
xA X T y A R Y z Z A
S
P yc
记为： a
f h f c c P0
倾斜误差 m0 a m a m0 yc0 hc xc,xc0 38 M
倾斜误差公式
a rc r0
rc sin sin f rc sin sin
2
2
i
yc , yc
0
r0 rc

y
c
m0 (m0)
a
m
y
0 c
rc a sin sin f
17
透视变换定义（Perspective Transform） 两个平面之间的中心投影变换，称为 透视变换。
透视变换中的特别点、线、面 （ Points、Lines、Planes ） 基本要素（S、P、T） 特殊面（3）： 特殊线（8）：
特殊点（9）：
18
1、像平面坐标系 2、像空间坐标系
o-xy S-xyz
x x x0 y y y0
21
航摄像片的外方位元素 确定像空系（或摄影光束）在地辅系中位置 和方向的元素叫做航摄像片的外方位元素。 像片的外方位元素有6个，其中3个是线元素， 即像空系的原点S在地辅系中的坐标；另外3个是 角元素，用以确定像空系三轴在地辅系中的方向。
三种角元素系统
、、 、 、 t、、 v
22
P d S
像片 中 心 投 影
问题 提出
A B
C c0
D d0
地面 投影 地形图23
地形图 a0
b0
如何建立中心投影关系下地面点与其像 点之间的数学关系？ 建立坐标系表示点位。 依据中心投影条件建立数学关系。
问题 提出
24
•旋转矩阵的性质 •像点和地面点的坐标变换
15
中心投影[Central Projection] 所有投射线或其延长线都通过一个固定点 的投影，叫做中心投影。 投影中心 S
阴位：投影中心位于物和像之间。 阳位：投影中心位于物和像同侧。 航摄像片是地面的中心投影。
16
中心投影的主要特征 • 点的中心投影一般是点。（特例） • 线段的中心投影一般是线段。（特例） • 相交线段的中心投影一般是相交线段。（特例） • 空间一组不与承影面平行的平行直线，其中心投 影为一平面线束。线束的顶点是由过投影中心并与 空间平行直线相平行的投射线与承影面的交点，称 为合点。 • 平面曲线的中心投影一般是平面曲线。 • 空间曲线的中心投影是平面曲线。
☆等比线上的像点没有倾斜误差。
40
投影误差定义(Projection Error) 当地面有起伏时， 高于或低于所选定的 基准面的地面点的像 点，与该地面点在基 准面上的垂直投影点 的像点之间的直线移 位。
投影误差
(n)o a0 a
S
A
H
h
B A0 ( N )O
41
投影误差公式 •水平像片的 投影误差公式：
x f y f
xA z A （ 1） yA zA
（ 3）
31
x f y f
a1 ( X X S ) b1 (Y YS ) c1 ( Z Z S ) a3 ( X X S ) b3 (Y YS ) c3 ( Z Z S ) a2 ( X X S ) b2 (Y YS ) c2 ( Z Z S ) a3 ( X X S ) b3 (Y YS ) c3 ( Z Z S )
分析
a1 x a 2 y a3 f X Xs ( Z Zs ) c x c y c f 1 2 3 Y Ys ( Z Zs ) b1 x b2 y b3 f c1 x c2 y c3 f 6个外方位元素 ： X , Y , Z ,,ω,κ, S S S
＋
ZT
( X ,Y , Z )
YT
A
D
XT
27
Z
两点两系
z
S
y
Y
x
f
o
X
一点两系
X x Y R y Z z
＋
两点一系
y
a
( x , y , f )
x
SaA共线
( X ,Y , Z ) A
x X T y R Y z Z
容 安 排
36
二、像片的投影误差
三、像片的倾斜误差 四、像点坐标的系统误差及其改正
• 倾斜误差定义 • 公式推导(重点、难点) • 倾斜误差性质
• 投影误差定义 • 公式推导（重点、难点） • 投影误差性质
37
倾斜误差定义（Tilt Error）
同摄站同主距的倾斜像片和水平像片沿等比线 重合时,地面点在倾斜像片上的像点与相应水平像 片上像点之间的直线移位。
通过航摄像片比例尺的分析可知：地形 起伏和像片的倾斜造成像比例尺的变化，其 实质就是地形起伏和像片的倾斜引起实际像 点位置相对于理想状态构像位置的变化。 地形起伏和像片的倾斜引起的这种像点 变化的规律是什么？ 在像片上如何消除这些因素带来的像点 位置的变化？
问题 提出
35
像片的几何特性
内
一、像片的比例尺
P d S
水平像片P0 d 改倾斜误差 和投影误差 S
A B 地形图 a0 b0
C c0
D d0
d0 平坦且水平的地面 T 44
a1 ( X X S ) b1 (Y YS ) c1 ( Z Z S ) xf a3 ( X X S ) b3 (Y YS ) c3 ( Z Z S ) a 2 ( X X S ) b2 (Y YS ) c2 ( Z Z S ) yf a3 ( X X S ) b3 (Y YS ) c3 ( Z Z S ) a1 x a 2 y a 3 f X Xs ( Z Zs) c1 x c 2 y c 3 f b1 x b2 y b3 f Y Ys ( Z Zs) c1 x c 2 y c 3 f
3
雷达摄影测量
目标
图像
信息
双介质摄影测量 X射线摄影测量
航天摄影测量 地形摄影测量 (地形图) 航空摄影测量 地面摄影测量 模拟摄影测量
解析摄影测量
数字摄影测量
4
非地形摄影测量 (其他用途)
近景摄影测量
显微摄影测量
摄影测量利用航摄像片获取所摄目标信息， 因此，航摄像片是摄影测量的基础。 摄影测量对影像质量有什么要求？ 在摄影时，必须满足什么条件？
3个内方位元素： x0 , y0 , f
3个地面点坐标： X ,Y , Z 2个像点坐标： x，y
32
空间后方交会、空间前方交会 光束法平差的基本公式 计算像片模拟数据
x f y f
a1 ( X X S ) b1 ( Y YS ) c1 ( Z Z S ) a3 ( X X S ) b3 ( Y YS ) c3 ( Z Z S ) a2 ( X X S ) b2 ( Y YS ) c2 ( Z Z S ) a3 ( X X S ) b3 ( Y YS ) c3 ( Z Z S )
28
像空系
点\坐标系 S—xyz x，y，-f xA，yA，zA
地辅系
S—XYZ
像点
a A
物点
X，Y，Z
xA X T yA R Y z Z A
x A a1 X b1Y c1 Z y A a2 X b2Y c2 Z z a X b Y c Z 3 3 3 A
•定义 •共线条件方程推导(重点、难点) •分析 •应用
25
S
f a
o
在理想情况下，摄影瞬间像 点、投影中心、物点位于同一条 直线上，以三点共线为基础建立 起来的描述这三点共线的数学表 达式，称之为共线条件方程式。
A
26
z
S
y
x
f
o
两点两系 一点两系 两点一系
y
a
( x , y , f ) x
3、摄影测量坐标系
4、地面辅助坐标系 5、大地坐标系
S-XYZ
OT-XTYTZT O-XGYGZG
19
原点、轴向、作用
z