金融数学第1节
- 格式:ppt
- 大小:1.15 MB
- 文档页数:60

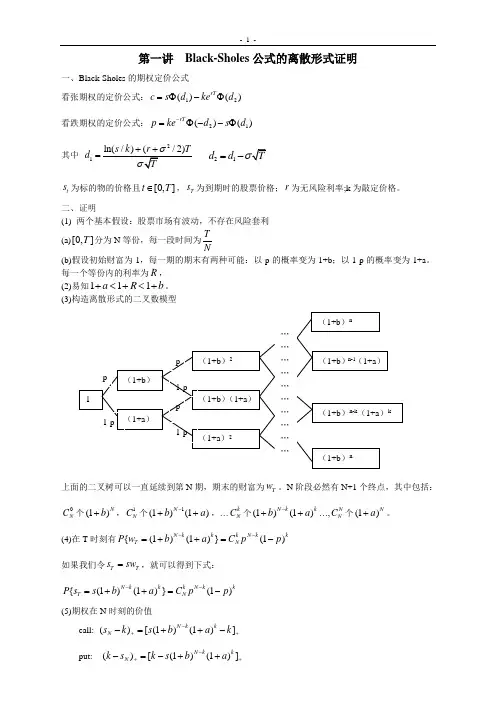
第一讲 Black-Sholes 公式的离散形式证明一、Black-Sholes 的期权定价公式看张期权的定价公式:12()()rT c s d ke d =Φ-Φ 看跌期权的定价公式:21()()rT p ke d s d -=Φ--Φ 其中21d =21d d σ=-t s 为标的物的价格且[0,]t T ∈,T s 为到期时的股票价格;r 为无风险利率;k 为敲定价格。
二、证明(1) 两个基本假设:股票市场有波动,不存在风险套利 (a)[0,]T 分为N 等份,每一段时间为T N(b)假设初始财富为1,每一期的期末有两种可能:以p 的概率变为1+b ;以1-p 的概率变为1+a 。
每一个等份内的利率为R , (2)易知111a R b +<+<+。
(3)构造离散形式的二叉数模型上面的二叉树可以一直延续到第N 期,期末的财富为T w 。
N 阶段必然有N+1个终点,其中包括:N C 个(1)N b +,1N C 个1(1)(1)N b a -++,…k N C 个(1)(1)N kk b a -++…,N N C 个(1)Na +。
(4)在T 时刻有{(1)(1)}(1)N k k k N k kT N P w b a C p p --=++=- 如果我们令T T s sw =,就可以得到下式:{(1)(1)}(1)N kk k N kkT N P s s b a C pp --=++=-(5)期权在N 时刻的价值call: ()[(1)(1)]N k kN s k s b a k -++-=++- put: ()[(1)(1)]N k kN k s k s b a -++-=-++()01()(1)[(1)(1)](1)NN k N kk N kkN NNk cE s k Cpp s b a k R --++==-=-++-+∑()1()(1)[(1)(1)](1)NN k N kk N kkN NN k pE k s Cpp k s b a R --++==-=--+++∑(6)看张和看跌期权的平价关系由步骤(5)可知:(1)N N Nk c p s R -=-+(7)收益率的换算因为T rR N=,所以连续复利elim (1)lim (1)rTNNN N rT R N→∞→∞=+=+。




《金融数学引论》复习提纲第一章 利息的基本计算 第一节 利息基本函数一. 累积函数a(t)与总量函数A(t)某一度量期的实际利率是指该度量期内得到的利息金额与此度量期开始时投资的本金金额之比,通常用字母i 来表示。
利息金额I n =A(n)-A(n-1)对于实际利率保持不变的情形,i=I 1/A(0); 对于实际利率变动的情形,则i n =I n /A(n-1); 二.单利和复利考虑投资一单位本金,(1) 如果其在t 时刻的积累函数为 a(t)=1+i*t ,则称这样产生的利息为单利;实际利率 )()()()(1111-+=---=n i in a n a n a i n(2) 如果其在t 时刻的积累函数为a(t)=(1+i)t ,则称这样产生的利息为复利。
实际利率 i i n =三.. 贴现函数一个度量期的实际贴现率为该度量期内取得的利息金额与期末的投资可回收金额之比,通常用字母d 来表示实际贴现率。
等价的利率i 、贴现率d 和贴现因子(折现因子)v 之间关系如下:,(1),1111,,,1d ii d i i d d iv d d iv v i d idi=+==-+=-==-=+四.名利率与名贴现率用()m i 表示每一度量期支付m 次利息的名义利率,这里的m 可以不是整数也可以小于1。
所谓名义利率,是指每1/m 个度量期支付利息一次,而在每1/m 个度量期的实际利率为()/m i m 。
与()m i 等价的实际利率i 之间的关系:()1(1/)m m i i m +=+。
名义贴现率()m d ,()1(1/)m m d d m -=-。
名义利率与名义贴现率之间的关系:()()()()m m m m i d i d m m m m-=⋅。
五.连续利息计算定义利息强度(利息力)为()()()()t A t a t A t a t δ''==, 0()ts ds a t e δ⎰=一个常用的关系式如下:()()11[1]1(1)[1]m p m p i d i v d e m pδ---+=+==-=-=要求:δ,,,,)()(p m d i d i ,之间的计算。



第一章货币概述本章重要概念等价交换原则:商品交换中,相互交换的两种商品必须具有相等的价值(即生产这两种产品时,必须耗费同样多的人类劳动),这就是等价交换原则。
简单的偶然的价值形式:人类社会最初的商品交换相对应的商品价值形式,是价值形式发展过程中的原始阶段。
当时只是有了剩余产品而交换,还没有专门的商品生产,商品的价值只是偶然地通过另一种商品表现出来,所以称简单的或偶然的价值形式。
总和的扩大的价值形式:处在相对价值形式上的商品的价值不仅表现在某一种商品上,而且表现在一系列其他商品上。
这种商品价值的表现形式就是总和的扩大的价值形式。
一般价值形式:即一切商品的价值共同表现在某一种从商品世界中分离出来而充当一般等价物的商品上。
货币价值形式:即一切商品的价值固定地由一种特殊商品来表现,这种特殊商品(黄金、白银)固定地充当一般等价物。
它是价值形式的最高阶段。
信用货币:信用货币是由国家和银行提供信用保证的流通手段。
它通常由一国政府或金融管理当局发行,其发行量要求控制在经济发展的需要之内。
信用货币包括辅币、现钞、银行存款、电子货币等形态。
货币量层次划分:货币量层次划分,即是把流通中的货币量,主要按照其流动性的大小进行相含排列,分成若干层次并用符号代表的一种方法。
价值尺度:货币在表现商品的价值并衡量商品价值量的大小时,发挥价值尺度的职能。
这是货币最基本、最重要的职能。
价格标准:指包含一定重量的贵金属的货币单位。
在历史上,价格标准和货币单位曾经是一致的,随着商品经济的发展,货币单位名称和货币本身重量单位名称分离了。
流通手段:货币充当商品流通的媒介,就执行流通手段职能。
贮藏手段:当货币由于各种原因退出流通界,被持有者当作独立的价值形态和社会财富的绝对化身而保存起来时,货币就停止流通,发挥贮藏手段职能。
支付手段:当货币作为价值的独立形态进行单方面转移时,执行着支付手段职能。
如货币用于清偿债务,支付赋税、租金、工资等所执行的职能。

