哈工大理论力学考研《理论力学Ⅰ》考研配套考研真题

格式：doc
大小：134.50 KB
文档页数：5

下载文档原格式

哈工大理论力学教研室《理论力学Ⅰ》(第7版)课后习题-点的合成运动(圣才出品)

图 7-4 解：以 M 为动点，水轮为动系，牵连运动轨迹为定轴转动，速度分析如图 7-5 所示。
图 7-5 由 va = ve + vr 在 x、y 两个方向上的分量得
va sin 60o = ve + vr sin va cos 60o = vr cos
7 / 42
圣才电子书

图 7-1
图 7-2
7-2 图 7-2 中的速度平行四边形有无错误？错在哪里？
1 / 42
圣才电子书十万种考研考证电子书、题库视频学习平台

答：都有错误，改正见图 7-3。
图 7-3 7-3 如下计算对不对？错在哪里？
图 7-4 （a）图 7-4（a）中取动点为滑块 A，动参考系为杆 OC，则 ve=ω·OA，va=cosφ （b）图 7-4（b）中 vBC=ve=vacos60°va=ωr 因为 ω=常量,所以，VBC=常量，（c）图 7-4（c）中为了求 aa 的大小，取加速度在 η 轴上的投影式：aacosφ-ac=0 所以答：（a）不对，va 的速度平行四边形画法不正确，正确图见图 7-5。（b）加速度的计算不正确。vBC 和 ω 为此瞬时的大小，不是任意时刻的速度和角速度故不能对时间求导。
其中 ρ 和 φ 是用极坐标表示的点的运动方程，aρ 和 aψ 是点的加速度沿极径和其垂直方向的投影。
答：如图 7-7 建立直角坐标系．xOy 与极坐标系 ρOφ。取动点 Q，动系 OA
4 / 42
圣才电子书

加速度合成（图 7-8）
十万种考研考证电子书、题库视频学习平台
aa=aen+aet+ar+ac
大小：？
方向：Hale Waihona Puke √ √ √ √图 7-7

哈工大理论力学教研室《理论力学Ⅰ》(第7版)课后习题-空间力系(圣才出品)

3-10 一均质等截面直杆的重心在哪里？若把它弯成半圆形，重心的位置是否改变？答：重心与形心重合，位于轴线中点。弯成半圆形，重心位置位于物体之外。
二、习题 3-1 槽形钢受力如图 3-1 所示。求此力向截面形心 C 简化的结果。
图 3-1 解：以 x 轴方向垂直纸面向外， y 轴方向水平向右， z 轴方向铅垂向上建立坐标系，计算各力的投影和对轴的矩，并分别求和，可得
MCx = −20 0.102 = −2.04kN m
MCz = −20 (0.035 − 0.0147) = −0.406kN m
解得
( ) r
r
MC = −2.04i − 0.406k kN m
5 / 31
圣才电子书十万种考研考证电子书、题库视频学习平台

答：令正方体边长为 a，则有
图 3-1
1 / 31
圣才电子书十万种考研考证电子书、题库视频学习平台

3-2 图 3-2 所示正方体上 A 点作用一个力 F，沿棱方向，问：（1）能否在 B 点加一个不为零的力，使力系向 A 点简化的主矩为零? （2）能否在 B 点加一个不为零的力，使力系向 B 点简化的主矩为零? （3）能否在 B,C 两处各加一个不为零的力，使力系平衡? （4）能否在 B 处加一个力螺旋，使力系平衡? （5）能否在 B,C 两处各加一个力偶，使力系平衡? （6）能否在 B 处加一个力，在 C 处加一个力偶，使力系平衡?
图 3-4 解：以 BC 为 x 轴正向，BA 为 y 轴正向，竖直向上为 z 轴正向建立坐标系，计算各力的投影和对轴的矩，并分别求和，可得：
3-5 图 3-5 所示正立方体的边长 a＝0.2 m，在顶点 A 沿对角线 AB 作用一力 F，其大小以对角线 AB 的长度表示，每 1 mm 代表 10 N。求向点 O 简化此力的结果。

哈工大理论力学教研室《理论力学Ⅰ》(第7版)章节题库-空间力系(圣才出品)

矩。已知：F＝1kN，a＝18cm，b＝c＝10cm。
图 3-6 解：解法一：利用力对点之矩与力对轴之矩的关系定理来计算。由于 CD 轴和 CE 轴均过 C 点，因此可以先计算力对 C 点之矩，再将其分别向 CD 轴和 CE 轴投影来求解。
4 / 17
圣才电子书十万种考研考证电子书、题库视频学习平台
1 17
圣才电子书十万种考研考证电子书、题库视频学习平台

图 3-2 【答案】C 【解析】先计算 F 在各轴上的投影大小
Fx = −F cos30。cos 60。, Fy = −F cos30。sin 60。, Fz = F sin 30。
再计算对各轴的矩
3．有重力为 W、边长为 a 的均质正方形薄板，与—重力为 0.75W、边长分别为 a 和 2a 的直角均质三角形薄板组成的梯形板，如图 3-3 所示。其重心的坐标（xc，yc）为（）。
A． B． C． D．
2 / 17
圣才电子书十万种考研考证电子书、题库视频学习平台

【答案】B
图 3-3
二、填空题 1.空间力系若不平衡，其简化的最后结果：或者是一个力，或者是______；或者是 ______。【答案】一个力偶；一个力螺旋【解析】空间任意力系简化的最终结果有 4 种情况：合力、合力偶、力螺旋和平衡。当主矢不为零，主矩为零或主矩不为零但主矢主矩垂直时，最终结果为合力；当主矢主矩均不为零，主矢与主矩平行或成任意角（不包括垂直角度时），最终结果为力螺旋；当主矢为零主矩不为零时，最终结果为合力偶；当主矢主矩均为零时，力系平衡。

（1）先将力 F 分解为沿坐标轴的三个分力如图 3-6（b）所示，其中有
代入数据可计算出
（2）计算力对过 C 点的三根正交轴之矩，因为有

哈工大理论力学教研室《理论力学Ⅰ》(第7版)课后习题-平面力系(圣才出品)

，所以 RA＝RB。与条件矛盾。
(5)不可以。同(1)。
(6)可以。满足条件的力有很多。
2-9 图 2-6 中 OABC 为正方形，边长为 a。已知某平面任意力系向 A 点简化得一主矢 (大小为 F＇RA)及一主矩(大小、方向均未知)。又已知该力系向 B 点简化得一合力，合力指向 O 点。给出该力系向 C 点简化的主矢(大小、方向）及主矩(大小、转向)。

(4)向 B 点简化得
十万种考研考证电子书、题库视频学习平台
，是否可能？
(5)向 B 点简化得
，是否可能？
(6答：(1)不可能。据“力的平移定理”，力可以平移，但不可以消失或改变大小。
(2)可以。同上。
(3)可以。同(1)。
(4)不可以。看 MA＝MB，则
图 2-1 解：以滑轮 B 为研究对象，进行受力分析，如图 2-2 所示。
由平衡方程可得
图 2-2
Fx = 0 Fy = 0
6 / 94
圣才电子书十万种考研考证电子书、题库视频学习平台

FBA + FBC cos 30 + F2 sin30 = 0 F1 + F2 cos 30 + FBC sin30 = 0 其中， F1 = F2 = P 。
2-11 不计图 2-7 中各构件自重，忽略摩擦。画出刚体 ABC 的受力图，各铰链均需画出确切的约束力方向，不得以两个分力代替。图中 DE//FG。
答：如图 2-8 所示。
图 2-7
图 2-8
5 / 94
圣才电子书十万种考研考证电子书、题库视频学习平台

二、习题 2-1 物体重 P＝20 kN，用绳子挂在支架的滑轮 B 上，绳子的另一端接在绞车 D 上，如图 2-1 所示。转动绞车，物体便能升起。设滑轮的大小、AB 与 CB 杆自重及摩擦略去不计，A，B，C 三处均为铰链连接。当物体处于平衡状态时，求拉杆 AB 和支杆 CB 所受的力。

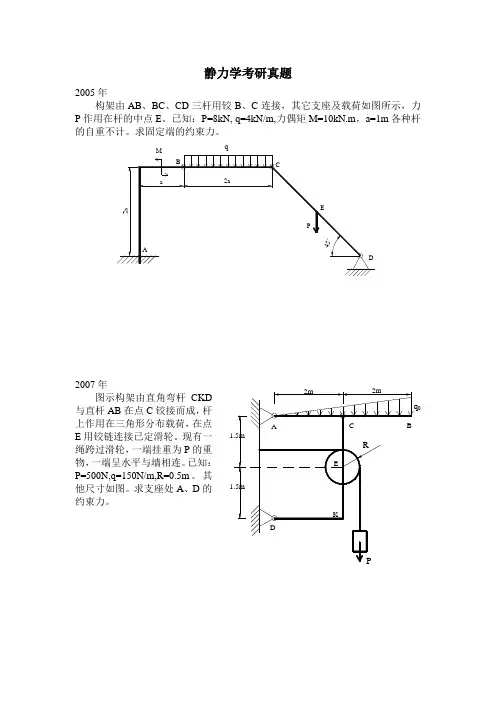
哈工大理论力学历年考研真题——静力学题经典题目

静力学考研真题2005年构架由AB、BC、CD三杆用铰B、C连接，其它支座及载荷如图所示，力P作用在杆的中点E。

已知：P=8kN, q=4kN/m,力偶矩M=10kN.m，a=1m各种杆的自重不计。

求固定端的约束力。

q2007年图示构架由直角弯杆CKD与直杆AB在点C铰接而成，杆上作用在三角形分布载荷，在点E用铰链连接已定滑轮。

现有一绳跨过滑轮，一端挂重为P的重物，一端呈水平与墙相连。

已知：P=500N,q=150N/m,R=0.5m。

其他尺寸如图。

求支座处A、D的约束力。

2002年图示构架，A 为固定铰链，B 处为光滑平面，各杆件自重不计。

已知：P1=P2=100kN ，L=5m,试求A 、D 、E 、H 各铰链处的约束力。

00年如图所示，平面构架的各杆自重不计，已知：q=1kN/m,L=1m,a=0.6m,EH=0.3m;在DE 杆上作用已力偶，其矩M=kN.m 。

试求铰链B 、D 、H 、A 的约束力。

L1999 年构架如图所示，各杆自重不计。

皆为铰链。

已知：q=50kN/m,M=80kN.m,L=1m 。

试求固定端A 和支座B 的约束力。

1994年图示平面结构，尺寸如图所示，AC 、BC 及DF 三杆重量不计，A 、D 、C 、E 均为光滑铰链连接，B 为滚动支座。

C 处作用有已知水平力P ，F 处受力偶作用，力偶矩为M 。

试求水平杆DE 与D 、E 处所收的约束力。

图示平面结构，其中水平梁由AB 与BD 组成，图中各杆件的自重不计。

C 、BK 、E 、G 、H 均为光滑的铰链。

已知：集中载荷P=qaN 均布载荷qN/m ；力偶矩M=qa.a 。

AC=CB=BK=KD=GH=AE=CG=BH=am 。

求插入端A 的约束力1990年图示构架，各杆的自重不计，A 、B 、C 、D 、E 、F 处均为光滑铰链连接。

已知M=50kN.m ，P=,45,θ=各尺寸如图所示。

CD 、BF 杆水平，ABC 杆铅垂。

哈工大理论力学教研室《理论力学Ⅰ》(第7版)配套题库-名校考研真题(中)(圣才出品)

−
1 4
R 2
+
R 2
解得
aet =
3 R2 6
所以，杆 O1A 的角加速度为 = aet = 3 2 ，逆时针方向。 2R 12
4．平面机构如图 7-9 所示。已知：VA＝0.6m/s ＝常量，L1＝1m，L2＝0.5m。在图示位置时，＝45o，杆 ED 在水平位置，且 AD＝DB。试求该瞬时杆 ED 的角加速度 αE。[北京科技大学 2011 研]
1 / 29
圣才电子书十万种考研考证电子书、题库视频学习平台

解：因为上部车条的速度要大于下部车条的速度。在相机曝光的时间内，上部车条因为速度大，会出现在不同的地方，所以照出来模糊；而下部车条速度小，相对静止，所以照出来清晰。
3．如图 6-2 所示，一质量为 m 的物体放在匀速转动的水平转台上，它与转轴的距离为 r。设物体与转台表面的摩擦系数为 μ。当物体不致因转台旋转而滑出时，求水平台的最大转速是多少。[中科院 2007A 研]
图 6-2 解：取物体进行受力分析。重力、支持力和摩擦力的合力维持了物体的圆周运动，此摩擦力不能大于最大静摩擦力。
ma = mr2 mg
解得
g r
2 / 29
圣才电子书

十万种考研考证电子书、题库视频学习平台
第 7 章点的合成运动
1．如图 7-1 所示，已知曲柄长度 OA＝r，OA 以匀角速度 ω 转动，连杆 AB 的中点 C 处连接一滑块 C，滑块 C 可沿导槽 O1D 滑动，图中连杆 AB＝ι。图示瞬时 O、A、O1 三点
由面积关系有
r02 −r2 = bvt
①
由式①对 t 求导得
−2r dr = bv

哈工大理论力学教研室《理论力学Ⅰ》(第7版)课后习题(第1~3章)【圣才出品】

19 / 142
圣才电子书十万种考研考证电子书、题库视频学习平台

图 2-3 答：支座约束力不相同，如图 2-4 所示。
图 1-4
图 1-5
1-6 将如下问题抽象为力学模型，充分发挥你们的想象、分析和抽象能力，试画出它们的力学简图及受力图。
（1）用两根细绳将日光灯吊挂在天花板上；（2）水面上的一块浮冰；（3）一本打开的书静止于桌面上；（4）一个人坐在一只足球上。
3 / 142
圣才电子书

答：如图 1-8 所示。
图 1-7
4 / 142
圣才电子书十万种考研考证电子书、题库视频学习平台

图 1-8 二、习题 1-1 画出图 1-1 各图中物体 A、ABC 或构件 AB、AC 的受力图。未画重力的各物体的自重不计，所有接触处均为光滑接触。
5 / 142
圣才电子书十万种考研考证电子书、题库视频学习平台
6 / 142
圣才电子书十万种考研考证电子书、题库视频学习平台

图 1-1 解：各物体的受力图如图 1-2 所示。
7 / 142
圣才电子书十万种考研考证电子书、题库视频学习平台
圣才电子书十万种考研考证电子书、题库视频学习平台
13 / 142
圣才电子书十万种考研考证电子书、题库视频学习平台
14 / 142
圣才电子书十万种考研考证电子书、题库视频学习平台

FD
图 1-4 1-3 画出图 1-5 中每个标注字符的物体的受力图，各题的整体受力图。未画重力的物体的自量均不计，所有接触处均为光滑接触。
15 / 142
圣才电子书十万种考研考证电子书、题库视频学习平台

哈工大理论力学教研室《理论力学Ⅰ》(第7版)章节题库-动能定理(圣才出品)

圣才电子书

十万种考研考证电子书、题库视频学习平台
第 12 章动量矩定理
一、选择题 1．图 12-1 所示无重刚杆 AB，两端各固连一个小球，其质量分别为 m1、m2。若 m1 ＞m2，不计空气阻力，则当杆 AB 在重力作用下由水平静止位置进入运动后（）落地。 A．两端同时 B．A 端先 C．B 端先 D．无法判断
图 12-10
解：系统初始静止，T1 = 0 ，当杆 AB 运动到与铅垂线夹角为时的动能为
下面建立与 vC 的关系。
4 / 25
圣才电子书十万种考研考证电子书、题库视频学习平台

垂线的夹角为常数，杆长为 l。
（3）图 12-8（c）：均质 L 型刚杆，质量为 m，在铅垂面内以等角速度 ω 绕轴 O 转动。
（4）图 I4-8（d）：质量为 m1 的滑块，沿水平直线运动，通过铰链 A，用长为 l 质量为 m2 的刚杆固结一垂球 B，重球质量为 m3。设图示瞬时，滑块的速度为 υ，杆 AB 绕 A 点转动的角速度为 ω。

履带
段合在一起是一个均质圆环，作平面运动，其动能为
因此，系统的总动能为
（2）图 12-8（b）：杆 0A 作锥形转动，取 dx 微段，其质量为 dm = m dx ，速度 l
v = xsin ，动能为
因此，杆 0A 总的动能为
（3）图 12-8（c）：L 型杆由 OA 和 AB 两部分组成，它们都作定轴转动。 OA 段： AB 段：则 L 型杆的动能为
D．
【答案】D
图 12-2
3．质量为 m 的均质细圆环半径为 R，其上固结一个质量也为 m 的质点 A（图 12-3）。细圆环在水平面上作纯滚动，图示瞬时角速度为 ω，则系统的动能为（）。

哈工大理论力学教研室《理论力学Ⅰ》(第7版)课后习题-刚体的平面运动(圣才出品)

3 / 63
圣才电子书

又 atBA⊥AB
十万种考研考证电子书、题库视频学习平台
所以当 w＝0 时，平面图形上两点的加速度在此两点的连线上投影相等。
8-8 如图 8-7 所示各平面图形均作平面运动，问图示各种运动状态是否可能？
图 a 中，aA 与 aB 平行，且 aA＝－aB。
图 b 中，aA 与 aB 都与 A，B 连线垂直，且 aA，aB 反向。
图 c 中，aA 沿 AB 连线，aB 与 AB 连线垂直。
图 d 中，aA，aB 都沿 A，B 连线，且 aB>aA。
图 e 中，aA，aB 都沿 A，B 连线，且 aA>a8B。
图 f 中，aA 沿 A，B 连线方向。
图 g 中，aA，aB 都与 AC 连线垂直，且 aB>aA。
6 / 63
圣才电子书十万ቤተ መጻሕፍቲ ባይዱ考研考证电子书、题库视频学习平台

则 atc＝ao·cosβ－at∞＝0 车轮角加速度由此可以求出速度瞬心，C 的加速度大小和方向。
图 8-5
图 8-6
8-7 试证：当 w＝0 时，平面图形上两点的速度在此两点连线上的投影相等。答：令两点为 A、B，如图 8-6 所示，由加速度的合成公式 aB＝aA+atBA+anBA 当 w＝0 时 anBA＝AB·w2＝0 则 aB＝aA+atBA
图 h 中，AB 上 AC，aA 沿 AB 线，aB 在 AB 线上的投影与 aA 相等。
图 i 中，aA 与 aB 平行且相等，即 aA＝aB。
图 j 中，aA，aB 都与 AB 垂直，且 vA，VB 在 AB 连线上的投影相等。
图 k 中，vA 与 vB 平行且相等，aB 与 AB 垂直，aA 与 vA 共线。

(NEW)哈工大理论力学教研室《理论力学》(第7版)笔记和课后习题(含考研真题)详解

目　录第1章　静力学公理和物体的受力分析1.1　复习笔记
1.2　课后习题详解
1.3　名校考研真题详解
第2章　平面力系
2.1　复习笔记
2.2　课后习题详解
2.3　名校考研真题详解
第3章　空间力系
3.1　复习笔记
3.2　课后习题详解
3.3　名校考研真题详解
第4章　摩　擦
4.1　复习笔记
4.2　课后习题详解
4.3　名校考研真题详解第5章　点的运动学
5.1　复习笔记
5.2　课后习题详解
5.3　名校考研真题详解第6章　刚体的简单运动
6.1　复习笔记
6.2　课后习题详解
6.3　名校考研真题详解第7章　点的合成运动
7.1　复习笔记
7.2　课后习题详解
7.3　名校考研真题详解第8章　刚体的平面运动8.1　复习笔记
8.2　课后习题详解
8.3　名校考研真题详解
第9章　质点动力学的基本方程9.1　复习笔记
9.2　课后习题详解
9.3　名校考研真题详解
第10章　动量定理
10.1　复习笔记
10.2　课后习题详解
10.3　名校考研真题详解
第11章　动量矩定理
11.1　复习笔记
11.2　课后习题详解
11.3　名校考研真题详解
第12章　动能定理
12.1　复习笔记
12.2　课后习题详解
12.3　名校考研真题详解
第13章　达朗贝尔原理。

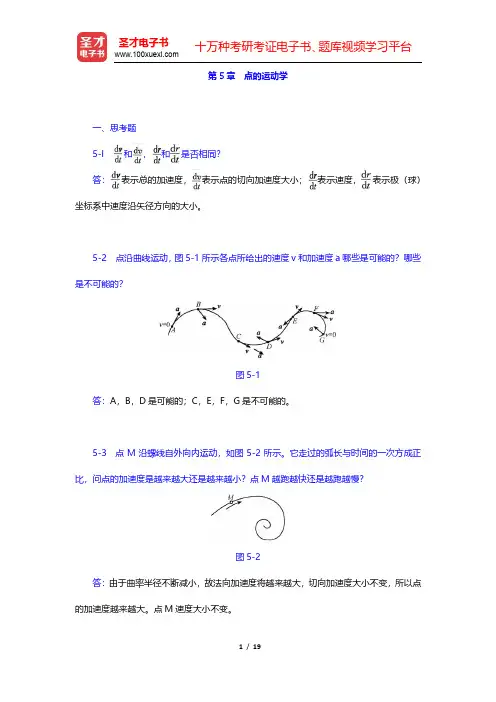
哈工大理论力学教研室《理论力学Ⅰ》(第7版)课后习题-点的运动学(圣才出品)

图 5-1 答：A，B，D 是可能的；C，E，F，G 是不可能的。
5-3 点 M 沿螺线自外向内运动，如图 5-2 所示。它走过的弧长与时间的一次方成正比，问点的加速度是越来越大还是越来越小？点 M 越跑越快还是越跑越慢？
图 5-2 答：由于曲率半径不断减小，故法向加速度将越来越大，切向加速度大小不变，所以点的加速度越来越大。点 M 速度大小不变。
（1）任一瞬时两动点的切向加速度必相同；（2）任一瞬时两动点的速度必相同；（3）两动点的运动方程必相同。答：由题设条件知，两动点任一瞬时切向加速度必相同，因此，任一瞬间两动点的速度必相同，运动方程必相同。
5-6 动点在平面内运动，已知其运动轨迹 y＝f（x）及其速度在 x 轴方向的分量 υx。判断下述说法是否正确：
（1）点沿曲线作匀速运动；（2）点沿曲线运动，在该瞬时其速度为零；（3）点沿直线作变速运动；（4）点沿曲线作变速运动。答：（1）at＝0，an＝a （2）an＝0,at＝a
（3）an＝0，a＝at （4）a＝an+at
5-8 点曲线运动时，下述说法是否正确：（1）若切向加速度为正，则点作加速运动；（2）若切向加速度与速度符号相同，则点作加速运动；（3）若切向加速度为零，则速度为常矢量。答：（1）不正确。若速度亦为正，则点作加速运动；若速度为负，则点作减速运动。（2）正确。（3）不正确。切向加速度为零时，速度大小不变，速度方向改变，所以速度不是常矢
（2）加速度沿 x 轴方向的分量 ax 可完全确定。其大小为（3）当 υx≠0 时，f'（x）为有限值，此时 υy＝f'（x）υx 故 υ 可求，υt，υn 也可求，所以 at，an 及全加速度 a 可求。
5-7 下述各种情况下，动点的全加速度 a、切向加速度 at 和法向加速度 an 三个矢量之间有何关系？

哈工大理论力学教研室《理论力学Ⅰ》(第7版)课后习题(第4~7章)【圣才出品】

答：物块不动，主动力的合力与铅垂线间的夹角 a＝12.5o，在摩擦角之内，故物体产生自锁现象。
4-6 如图 4-5 所示，用钢楔劈物，接触面间的摩擦角为φf。劈入后欲使楔不滑出，问钢楔两个平面间的夹角θ应该多大？楔重不计。
图 4-5 答：处于临界状态时，受力分析如图所示，由几何关系可知，欲使楔形不滑出，须满足
动物体时，若 A、B 两处均未达临界状况，此时不能使用静摩擦定律
则
不能分别求出 A、B 两处的静滑动摩擦力。若 A 处已达临界状态，且力 F 为已知，则可以
分别求出 A、B 两处的静滑动摩擦力。
4-8 汽车匀速水平行驶时，地面对车轮有滑动摩擦也有滚动摩阻，而车轮只滚不滑。汽车前轮受车身施加的一个向前推力 F（图 4-7a），而后轮受一驱动力偶 M，并受车身向后的反力 F’（图 4-7b）。试画全前、后轮的受力图。在同样摩擦情况下，试画出自行车前、后轮的受力图。又如何求其滑动摩擦力？是否等于其动滑动摩擦力 FN？是否等于其最大静摩擦力？
答：前轮摩擦力
图 4-7
后轮摩擦力
均不等于滑动摩擦力或最大静摩擦力。
4-9 重为 P，半径为 R 的球放在水平面上，球对平面的滑动摩擦因数是 fs，而滚阻系数为δ，问：在什么情况下，作用于球心的水平力 F 能使球匀速转动？
答：使球匀速转动的条件是：当
4 / 129
圣才电子书十万种考研考证电子书、题库视频学习平台
图 4-1
图 4-2
答：如图所示，由
，可得摩擦力 Fs＝100N。因为此时为静摩擦，故不可以用
公式
4-2 如图 4-2 所示，试比较用同样材料、在相同的光洁度和相同的胶带压力 F 作用下，乎胶带与三角胶带所能传递的最大拉力。

哈工大理论力学教研室《理论力学Ⅰ》(第7版)章节题库-刚体的平面运动(圣才出品)

第8章刚体的平面运动一、选择题1．图8-1所示平面图形上A、B两点的加速度与其连线垂直且ɑA≠ɑB，则此瞬时平面图形的角速度ω、角加速度α应该是（）。

A．ω≠0，α＝0B．ω＝0，α≠0C．ω＝0，α＝0D．ω≠0，α≠0图8-1【答案】B2．图8-2所示各平面图形的速度分布为：（a）v A＝－v B，v A不垂直AB，这种速度分布是（）。

A．可能的B．不可能的不垂直AB，，这种速度分布是（）。

A．可能的B．不可能的图8-2【答案】B；B3．在图8-3所示机构中，则ω1（）ω2。

A．＝B．＞C．＜图8-3【答案】C4．在图8-4所示机构的几种运动情况下，平面运动刚体的速度瞬心为：（a）（）；（b）（）；（c）（）；（d）（）。

A．无穷远处B．B点C．A、B两点速度垂线的交点D．A点E．C点图8-4【答案】D；B；A；C5．已知图8-5所示平面图形上B点的速度v B，若以A为基点，并欲使是B点相对于A点的速度，则A点的速度v A（）。

A．与AB垂直B．沿AB方向，且由A指向BC．沿AB方向，且由B指向AD．与AB成φ角图8-5【答案】B二、填空题1．边长为L的等边三角形板在其自身平面内运动，已知B点的速度大小为，方向沿CB，A点的速度沿AC方向。

如图8-6所示，则此时三角板的角速度大小为______；C点的速度大小为______。

图8-6【答案】2．已知作平面运动的平面图形上A点的速度v A，方向如图8-7所示。

则B点所有可能速度中最小速度的大小为______，方向______。

【答案】；沿AB方向图8-73．已知作平面运动的平面图形（未画出）上某瞬时A点的速度大小为v A，方向如图8-8所示，B点的速度方位沿mn，AB＝l，则该瞬时刚体的角速度ω为______,转向为______。

【答案】；顺时针图8-8三、判断题1．作平面运动的平面图形上（瞬时平移除外），每一瞬时都存在一个速度瞬心。

（）【答案】对2．研究平面运动图形上各点的速度和加速度时，基点只能是该图形上或其延展面上的点，而不能是其他图形（刚体）上的点。

哈工大理论力学教研室《理论力学Ⅰ》(第7版)课后习题-静力学公理和物体的受力分析(圣才出品)

第二部分课后习题第1章静力学公理和物体的受力分析一、思考题1-1 说明下列式子与文字的意义和区别。

（1）F1＝F2，（2）F1＝F2，（3）力F1等效于力F2。

答：（1）力F1和F2，大小相等，方向相同；（2）F1和F2大小相等；（3）F1和F2的大小相等，方向和作用线相同。

1-2 试区别F R＝F1＋F2和F R＝F1＋F2两个等式代表的意义。

答：F R＝F1＋F2表示F R是任意方向上两个力F1和F2的合力，合力F R的大小和方向由平行四边形法则确定；F R＝F1＋F2表示F R是同方向上两个力F1和F2的合力，合力F R的大小为F1和F2的大小的和，方向与F1和F2的方向相同。

1-3 图1-1（1）～1-1（4）中各物体的受力图是否错误？如何改正？图1-1答：均有错，正确图1-2。

图1-21-4 刚体上A点受力F作用，如图1-3所示，问能否在B点加一个力使刚体平衡？为什么？图1-3答：不能。

当在B点施加力F时，不能同时保证，故不能平衡。

1-5 如图1-4所示结构，若力F作用在B点，系统能否平衡？若力F仍作用在B点，但可任意改变F的方向，F在什么方向上结构能平衡？答：不能。

β在如图范围内可以令结构平衡，如图1-5所示。

图1-4图1-51-6 将如下问题抽象为力学模型，充分发挥你们的想象、分析和抽象能力，试画出它们的力学简图及受力图。

（1）用两根细绳将日光灯吊挂在天花板上；（2）水面上的一块浮冰；（3）一本打开的书静止于桌面上；（4）一个人坐在一只足球上。

答：如图l-6所示。

图1-61-7 若将图1-7中力F作用于三铰拱的铰链C处的销钉上，所有物体重量不计。

（1）试分别画出左、右两拱及销C的受力图；（2）若销钉C属于AC，分别画出左、右两拱的受力图；（3）若销钉C属于BC，分别画出左、右两拱的受力图。

图1-7答：如图1-8所示。

图1-8二、习题1-1 画出图1-1各图中物体A、ABC或构件AB、AC的受力图。

哈尔滨工业大学808理论力学历年考研真题(含部分答案)专业课考试试题

目　录
2014年哈尔滨工业大学808理论力学考研真题
2012年哈尔滨工业大学808理论力学考研真题
2009年哈尔滨工业大学808理论力学考研真题
2004年哈尔滨工业大学808理论力学考研真题
2002年哈尔滨工业大学416理论力学考研真题及答案
2001年哈尔滨工业大学理论力学考研真题及答案
2000年哈尔滨工业大学理论力学考研真题及答案
1999年哈尔滨工业大学理论力学考研真题及答案
1998年哈尔滨工业大学理论力学考研真题及答案
1997年哈尔滨工业大学理论力学考研真题及答案
1995年哈尔滨工业大学理论力学考研真题
2014年哈尔滨工业大学808理论力学考研真题。

哈工大理论力学教研室《理论力学Ⅰ》(第7版)课后习题-刚体的简单运动(圣才出品)

可得
当
时，
。
解得，Leabharlann ，6-5 如图 6-7 所示，曲柄 CB 以等角速度 ωO 绕 C 轴转动，其转动方程为＝ωOt。
滑块 B 带动摇杆 OA 绕轴 O 转动。设 OC＝h，CB＝r。求摇杆的转动方程。
7 / 16
圣才电子书

十万种考研考证电子书、题库视频学习平台
杆 BC 的运动规律以及当曲柄与水平线间的交角 φ 为 30°时，导杆 BC 的速度和加速度。
图 6-1 解：建立图 6-2 所示坐标系，由于刚体平动，所以选取 O1 为研究对象，可得
所以
当
时， t=
。
24
解得
4 / 16
圣才电子书十万种考研考证电子书、题库视频学习平台

6-2 各点都作圆周运动的刚体一定是定轴转动吗？答：不一定，刚体作平动时，各点也可能都作圆周运动。
6-3 满足下述哪些条件的刚体运动一定是平移？ ①刚体运动时，其上有不在一条直线上的三点始终作直线运动。 ②刚体运动时，其上所有点到某固定平面的距离始终保持不变。 ③刚体运动时，其上有两条相交直线始终与各自初始位置保持平行。 ④刚体运动时，其上有不在一条直线上的三点的速度大小、方向始终相同。答：①②不一定是平移；③④一定是平移。
6-7 刚体作定轴转动，其上某点 A 到转轴距离为 R。为求出刚体上任意点在某一瞬时
的速度和加速度的大小，下述哪组条件是充分的？
（1）已知点 A 的速度及该点的全加速度方向；
（2）已知点 A 的切向加速度及法向加速度；
（3）已知点 A 的切向加速度及该点的全加速度方向；
（4）已知点 A 的法向加速度及该点的速度；
圣才电子书

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

哈工大理论力学考研《理论力学Ⅰ》考研配套重点考
研真题
第一部分名校重点考研真题
第1章静力学公理和物体的受力分析
1．如图1-1所示，轻质杆与周围环境间无摩擦，试画出物体的受力分析图。

[中科院2007研]
（a）（b）
图1-1
解：如图1-2（a）、图1-2（b）所示受力分析图。

（a）（b）
图1-2
图1-2（b）中三力汇交于一点。

2．如图1-3所示，一根轻质直杆AB的A端与铰链支座相连，与墙构成45度角，在距离B端1／4杆长处系有一水平细绳。

若在距离B点2／5杆长处作用一竖直向下的力F，试作出直杆的受力分析图。

[中科院2007A研]
图1-3
解：如图1-4所示。

图1-4
三力汇交于一点。

4．图15-5示力学系统由质量为m、半径为r的匀质小圆柱A和一质量为m、长为3L的匀质刚杆AB组成，在O点用光滑铰链连接。

圆柱A可在半径为（L＋r）的圆弧槽内滚动而不滑动。

AB杆与可绕固定水平轴O摆动，在C点连接一刚度为k的水平弹簧，当＝0°时弹簧为原长。

试用拉格郎日方程求系统在图4示铅垂面内作微小振动的运动微分方程及微振动的周期。

[浙江大学2008研]
图15-5 解：取整个系统为研究对象，以为广义坐标。

系统的动能为
选取弹簧原长位置为零势能点，则系统势能为
故系统的拉格朗日函数为
求各偏导数
代入拉格朗日方程中，有
因为做的是微幅振动，可取并略去高阶小量含的项。

可得系统的微振动方程为
故系统微振动的固有频率为
微振动的周期为
5．在图15-6所示系统中，已知：匀质圆球A的半径为r、质量为m，楔块B的质量为M，置于光滑水平面上，斜面的倾角为θ，圆球沿楔块斜面作纯滚动。

试求：（1）以φ和X为广义坐标，用拉氏方程建立系统的运动微分方程；
（2）圆球A的角加速度ε和楔块B的加速度a。

（已知M＝4m）[中科院2008研]
图15-6
解：取整个系统为研究对象，系统具有两个自由度。

如题取坐标x和圆柱体的转角
为广义坐标。

可运用运动学原理求解。

以A的圆心O为动点，B为动系，则根据速度合成公式有：。

系统的动能为：
系统势能为：
拉格朗日函数为：
代入拉式方程：
化简得：
解得：。