理论力学哈工大第八版答案
- 格式:docx
- 大小:3.25 MB
- 文档页数:48



第八章 点的合成运动1.如图所示,光点M 沿y 轴作谐振动,其运动方程为0x =,)acos(kt y β+=如将点M 投影到感光纪录纸上,此纸以等速c v 向左运动。
求点M 在纪录纸上的轨迹。
解:t v x 0v dtx d )v (v v c c c x x ='⇒=-'=-+'= )kt cos(a y dtdydt y d v v y y β+='⇒='⇒'= ⎪⎪⎭⎫⎝⎛+'='βx v k cos a y c2.如图所示,点M 在平面Ox′y′中运动,运动方程为cost)40(1x -=',40sint y ='式中t 以s 计,x '和y '以mm 计。
平面Ox′y′又绕垂直于该平面的O 轴转动,转动方程为rad t =ϕ,式中角ϕ为动坐标系的x '轴与定坐标系的x 轴间的夹角。
求点M 的相对轨迹和绝对轨迹。
解:相对轨迹:22240y 40)x (='+-'绝对轨迹:j i i ϕϕsin cos +=',j i j ϕϕcos sin +-=',)cos sin 40sint()sin cost)(cos 40(140sint cost)40(1j i j i j i r r ϕϕϕϕ+-++-='+'-='=)cost sint 40sint()t sin cost)(cost 40(1j i j i +-++-=j i 40sint )140(cost +-= )140(cost x -=,40sint y =22240y 40)(x =++3.水流在水轮机工作轮入口处的绝对速度15m/s v a =,并与直径成60°角,如图所示。
工作轮的外缘半径R=2m ,转速30r/min n =。
为避免水流与工作轮叶片相冲击,叶片应恰当地安装,以使水流对工作轮的相对速度与叶片相切。

1、二力杆:只在两个力作用下平衡的构件。
2、静力学公理:1)平行(力的平行四边形法则):作用于物体上同一点的两个力,可以合成为一个合力,合力也作用于该点,合力的大小和方向,由这两个力构成的平行四边形的对角线确定。
刚体或者变形体都适用。
2)平衡(二力平衡公理):作用于刚体上的两个力,使刚体处于平衡的必要和充分条件是这两个力的大小相等,方向相反,且在同一直线上。
只适用于刚体。
3)加减(加减平衡力系公理):在作用于刚体上的任意力系中,加上或减去任意的平衡力系,并不改变原力系对刚体的作用。
只适用于刚体。
(1)可传(力的可传性原理):作用于刚体上某点的力,可以沿着它的作用线移动到刚体上的任意一点,并不改变该力对刚体的作用。
(2)三交汇(三力平衡交汇定理):作用于刚体上三个相互平衡的力,其中两个力的作用线汇交于一点,则此三力必在平面上,且第三个力的作用线也通过该汇交点。
4)相互(作用与反作用定律):作用力和反作用力总是同时存在,大小相等、方向相反,沿同一直线,分别作用在两个相互作用的物体上。
对刚体或变形体都适用。
5)刚化(刚化原理):变形体在某一力系作用下处于平衡,若将此变形体刚化为刚体,则平衡状态保持不变。
3、自由体和非自由体:运动不受限制的物体称为自由体;运动受到限制的物体称为非自由体。
4、两力相等和两个力等效不是一回事,力相等(大小、方向、作用点),力等效(根据力的可传递性原理,作用点可不一样,教材第7页;一个合力可以与力系等效,但合力不等于力系)。
平衡力系:物体处于平衡状态时,作用于物体上的力系。
等效力系:如果作用于物体上的力系可以用另一个力系代替,二不改变物体的原有状态。
5、约束反力,存在于相互接触之处,与约束所能限制的位移方向相反。
光滑铰链约束特点:构件只能绕销钉的轴线转动,而不能相对移动。
6、各种约束的约束特点:柔性约束:方向沿着绳索中心线而背离物体。
光滑面约束:约束反力作用在接触点,沿接触面的公法线指向被约束物体。


第一章一.1.√ 2.× 3.√4(a)×(b)×(c)×(d)×二.1.A 2.ACD 3.D三.1.二力平衡是两个力作用在同一刚体上,作用反作用定律是两个力作用在两个物体上。
2.二力杆、可动铰支座,光滑接触面约束、绳索的约束,固定铰支座,销钉。
3.等值、同向、共线4.滑移矢量第二章一. 1.× 2.√ 3.√ 4.√ 5.√二.1.C 2.A 3.D 4. B 5.B三1.2、 2 2.-F1cosα1、F2sinα2、-F3sinα3、F4cosα43.136.6,70.04.m5.81.17N与水平方向成60度角,左斜向上第三章一、1.√ 2.√ 3.√ 4.√ 5.×二、1.D 2.C 3.B B 4.D 5.C三.1.10KN,→ 2.10/a,←m/a ,沿HE方向 4. 2P,↑ 5.力偶M=40顺时针方向。
第四章一、1.× 2.√ 3.× 4.× 5.√二、1.A 2.D 3.D 4.A 5.B三、1.Fsinφ、-Fcosθcosφ、Fcosθcosφc+Fsinφb 2.-60N,320Nm3. 0,-Fa/2,Fa4 4. 5.Fasinφ第五章一、1.× 2.× 3.× 4.× 5.√二、1.C 2.B 3.C 4.bc 5.B三、1.滑动,28.862. 6.7KN3. ︒1054.m f ϕtan =5.主动力,自锁现象第六章一、1.√ 2.√ 3.× √ × 4.× 5.×二、1.B 2.C 3.C三、1.位移变化的快慢 2.静止或匀速直线运动 变速直线运动匀速曲线运动变速曲线运动 3.无关 4.MM /t '∆ 5.y=x/3第七章一、1.× 2.√ 3.× 4.× 5.√二、1.B 2.ADFG 3.A B A B 4.B 5.A C三、1.2r ω← 22r ω↑ 2.平动 定轴转动3.(1)22222r r r r r r ωαω、、(2)22r r r r r r ωαωωαω、、 、、(3)2L L ωαωω、L 、、4.反比 反比 5.增大 加速第八章一、1.√ 2.√ 3.√ 4.× 5.×√二、1.A 2.D 3.C 4.D 5.B B三、1.动系 动点 2.(1)A 上AB 接触点,OB ,地面(2)水平向右直线运动,沿OB 直线,绕O 轴转动(3)v 3,v 1=v A ,v 2 3.(a )O 2A 上A 点,O 1B 杆(b)滑块A ,OB 杆(c)接触点A 1,CB 杆 (d )圆环M ,OA 杆 (e )A 2,圆轮4.ωL ωL5. -ω2bsinωt 、ω2 L第九章1.×2.×3.√4.×5.×二、1.B 2.B A 3.C 4.B 5.B A三、1.平面运动,平面运动 瞬时平动 定轴转动。

理论力学Ⅰ第 8 版课后习题答案目录:
第一章静力学公理和物体的受力分析
第二章平面力系
第三章空间力系
第四章摩擦
第五章点的运动学
第六章刚体的简单运动
第七章点的合成运动第
八章刚体的平面运动
第九章质点动力学的基本方程
第十章动量定理
第十一章动量矩定理
第十二章动能定理
第十三章达朗贝尔定理
第十四章虚位移定理
第一章
后面章节的课后答案请关注.微-.信.公众号:学糕
后面章节的课后答案请关注.微-.信.公众号:学糕
第二章
后面章节的课后答案请关注.微-.信.公众号:学糕
后面章节的课后答案请关注.微-.信.公众号:学糕
后面章节的课后答案请关注.微-.信.公众号:学糕
后面章节的课后答案请关注.微-.信.公众号:学糕
后面章节的课后答案请关注.微-.信.公众号:学糕
后面章节的课后答案请关注.微-.信.公众号:学糕
后面章节的课后答案请关注.微-.信.公众号:学糕。
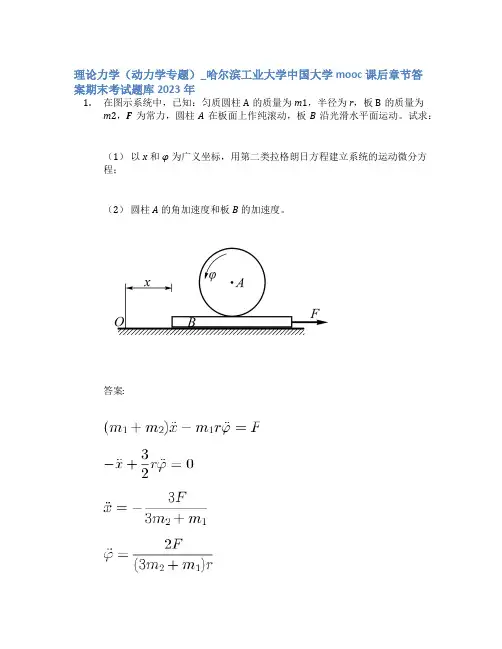
理论力学(动力学专题)_哈尔滨工业大学中国大学mooc课后章节答案期末考试题库2023年1.在图示系统中,已知:匀质圆柱A的质量为m1,半径为r,板B的质量为m2,F为常力,圆柱A在板面上作纯滚动,板B沿光滑水平面运动。
试求:(1)以x和φ为广义坐标,用第二类拉格朗日方程建立系统的运动微分方程;(2)圆柱A的角加速度和板B的加速度。
答案:2.图示质量为m的小球M放在半径为r的光滑圆管内,并可沿管滑动。
如圆管在水平面内以匀角速度ω绕管上某定点A转动,试求小球沿圆管的运动微分方程。
答案:3.匀质杆AB的质量m=10kg ,长l=4m ,在光滑的水平面内运动,其质心速度v C=20m/s,方向垂直于A,角速度ω=10rad/s ,转向如图示。
当杆的A 端突然固定时,试求:(1)杆的角速度;(2) 杆端A的碰撞冲量。
答案:ω2=10 rad/sI=04.图示物块A的质量为m,均质杆OB的质量为1.5m,长为l,上、下两弹簧的刚度系数分别为2k与k。
在平衡位置时,弹簧处于铅垂,而杆OB处于水平。
试求系统的主振动频率。
若给杆以微小的起始角速度ω0时,物块A 的速度等于零,求物块A的运动方程。
答案:5.重P1为180N的矩形框架绕水平轴AB以角速度2πrad/s 转动;框架的C,D上又安装重P2为120N的飞轮M,如图所示。
飞轮的转速为n=1800r/min,飞轮对自转轴的回转半径ρ=100 mm,CD=300 mm,AB=600 mm。
求:(l)在轴承C与D上的陀螺力;(2)轴承A和B上的全压力;(3)欲使轴承A上的压力为零时,飞轮的自转角速度。
答案:F C=F D=483.4N;F A=91.7N, F B=391.6N;ω=117rad/s6.长为l、单位长度质量为ρ的链条,从板上小孔向下降落。
最初,当y很小时,链条处于静止,并不计摩擦。
在图a中,假设链条在通过小孔前都是静止的;在图b 中,假设任何时刻链条各节都具有相同的速度值。