几何画板 课件设计 圆锥曲线的形成和立体图形的侧面展开_百度.
- 格式:doc
- 大小:202.50 KB
- 文档页数:23


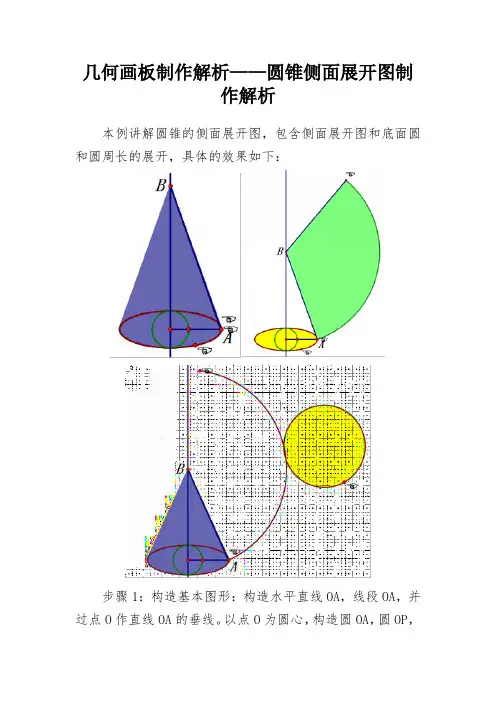
几何画板制作解析——圆锥侧面展开图制作解析本例讲解圆锥的侧面展开图,包含侧面展开图和底面圆和圆周长的展开,具体的效果如下:步骤1:构造基本图形:构造水平直线OA,线段OA,并过点O作直线OA的垂线。
以点O为圆心,构造圆OA,圆OP,在圆OA上任意构造一点H,连接OH,与圆OP交于点I,过点H作直线OA的垂线,过点I作刚才垂线的垂线IJ。
依次选中点H和点J,点击“构造”—“轨迹”这样就可以得到点J的轨迹。
步骤2:在过点O的垂线上,构造一点B,构造线段AB,并度量线段AB和OA的长度。
再计算圆锥侧面展开图(扇形)的圆心角。
利用公式“底面圆周长=扇形弧长”,得到扇形圆心角。
鼠标选中点A和线段AB,双击点B,点击“变换”—“旋转”,旋转角度选择标记角度,用鼠标点击刚才计算得到的旋转角,得到点A’和线段BA’;依次选择点B,A,A’,点击“构造”—“圆上的弧”。
选中弧,点击“构造”—“弧内部”—“扇形内部”,颜色选择绿色,效果如右下图所示。
步骤3:构造弧AA’上任意一点D,度量点D在弧上的点值,点击“数据”,执行1-D在弧AA’上”计算,为了便于后面操作,让圆锥的展开更加直观,将刚才的计算进行修改,执行“(1-D在弧AA’上)-trunc(1-D在弧AA’上)×0.01,依次选择点B,A,D,点击“构造”—“圆上的弧”,选中弧AD,点击“构造”—“弧内部”—“扇形内部”。
选中圆O 和处理后的点值,点击“绘图”—“在圆上绘制点”,得到点E ,依次选中点O,A,E 三点,点击“构造”—“圆上的弧”,得到点F 。
依次选择点M,H,J 三点,点击“度量”—“比”,得到MJ/MH 的值,过点F 作虚线的垂线,交点为点G ,然后双击点G (默认为缩放中心),单击点F ,点击“变换”—“缩放”,缩放比选择MJ/MH 的值,得到点F ’。
构造线段BF’,选中线段BF’和点F,点击“构造”—“轨迹”,就可以得到圆锥的侧面,拖动点D就可以实现圆锥侧面的展开与还原。

3D课件分享——圆锥曲线的形成
写在前面:
本文动态课件下载方式:
(长按屏幕,直接复制粗体字在后台回复)
后台回复:圆锥曲线
圆锥曲线的形成
主要内容:
1、主要从3D模型以及2D平面给大家动态展示高中圆锥曲线的形成。
2、动态课件的打开方式以及使用方式。
多图预警!第一part
首先给大家介绍各个滑条的作用,
第一、改变平面的旋转角度
第二、改变圆锥的形态
接着给大家看个总汇,
各个曲线如何形成。
下面逐个介绍:
在β=30°,b=4.1的时候,只改变平面旋转角度,
一、椭圆
先来个椭圆的形成的动态图
静态图——俯视图
二、抛物线
静态图
三、双曲线
静态图
下面再来个平面内的圆锥曲线形成
一、椭圆第一定义
二、抛物线定义
第二part课件打开方式以及使用方式
课件打开分成两种模式:
一、用geogebra软件打开(需要安装geogebra软件)
二、用IE浏览器或者是谷歌浏览器打开(无需安装软件;适用于无网络情况)
使用方式:
直接用IE浏览器打开“HTML”格式的文档,拖动滑条即可。


圆锥的侧面展开图圆锥的侧面展开图圆锥是一种立体图形,由一个圆形底面和一个顶点连接的直线组成。
在几何学中,我们经常使用侧面展开图来描述立体图形的形状和结构。
侧面展开图是将立体图形展开,使我们能够更好地理解其构造和组成。
首先,我们来看一下圆锥的基本特征。
圆锥的底面是一个圆形,用于提供稳定的支撑面。
圆锥的侧面是由从顶点连接到底面边缘的直线组成,这些直线被称为母线。
圆锥的顶点是连接底面和侧面的中心点。
为了绘制圆锥的侧面展开图,我们需要将圆锥展开成一个平面图形。
这可以通过将侧面按照一定顺序剪开,并展开到一个平面上来实现。
在展开的过程中,我们需要保持底面的圆形形状不变,并确保侧面的母线与底面保持相对位置不变。
展开后的侧面图是由一系列直线段构成的。
这些直线段代表了圆锥的侧面母线。
从顶点开始,我们可以看到侧面的直线段逐渐向底面延伸,并最终连接到底面边缘上。
展开后的侧面图呈现出一种锥形的形状,底面呈圆形,顶点在图形的中心位置。
圆锥的侧面展开图能够帮助我们更好地理解圆锥的结构和构造。
通过展开图,我们可以清晰地看到圆锥的母线如何连接到底面,并形成一个锥形的形状。
展开图还可以帮助我们计算圆锥的表面积和体积,以及分析其特性和功能。
在实际应用中,圆锥的侧面展开图被广泛应用于制作纸模、设计建筑物、制作工艺品等领域。
通过将圆锥展开成一个平面图形,我们可以更方便地制作和操作这些物品,并确保其形状和结构的准确性。
总结一下,圆锥的侧面展开图是将圆锥展开成一个平面图形以展示其构造和形状的方法。
通过展开图,我们可以更好地理解圆锥的特征和结构,并在应用中应用展开图进行设计和制作。
展开图提供了一种直观和清晰的方式来描述圆锥的形状和组成,对于学习和应用圆锥的几何学非常有帮助。


《几何画板》课件制作圆锥曲线的形成选题:圆、椭圆、抛物线、双曲线这四种曲线可以看作不同的平面截圆锥面所得到的截线,故它们统称为圆锥曲线。
在中学数学教学中,很难用实物教具演示圆锥曲线的形成过程。
在学习之初,学生很难对圆锥曲线的形成有一个直观的认识。
现利用几何画板模拟不同的平面截圆锥面的过程,动态演示不同圆锥曲线及截面的形成,为高中数学圆锥曲线的学习作引入。
这样设计使学生对抽象的圆锥曲线概念有一个更感性的认识,更便于学生理解圆锥曲线的实际意义。
原理:圆锥面被一平面所截所得的曲线形有:圆、椭圆、抛物线、双曲线。
制作过程:圆锥曲线的构造1.构造能够控制截面作移动和倾斜变化的示意图1作小椭圆:利用同心圆法作椭圆,椭圆的长半轴为OA,短半轴为OB;(1)过O作OA的垂线,在垂线的上方任取一点H,作线段HO并隐藏垂线。
用线段连接AH,分别在线段 HO和AH上任取点C和点D,连接CD;(2)作截面:以点C为圆心,以小线段r为半径作圆。
在上半圆上任取一点E,隐藏小圆。
依次选定点E和点C并标记为向量,把点C 按标记向量平移得到点E′,再依次选定点C和点D并标记为向量,把点E和E′按标记向量平移得到点F和F′。
同时选定点E、F、F′和E′,用线段相连得截面EFF′E′,并涂上浅黄色,如图 1所示:Br b ()a ()圆锥截面的形成'<图 1> <图 2>注意:利用示意图控制截面作移动和倾斜变化:1)拖动点A 或点B ,可以改变椭圆的大小;2)拖动点C 或点D ,可以使截面EFF ′E ′上下移动或上下倾斜;3)拖动点E ,可以使截面左右倾斜或翻转。
2.构造圆锥面被截面所截形成圆锥截面曲线的过程(1)做大椭圆:利用同心圆法作椭圆,椭圆的长半轴O ′A ′=2|OA|,短半轴O ′B ′=2|OB|,椭圆中心为O′;(2)作圆截面:依次选定点O 和点H 并标记为向量,把点O ′按标记向量平移两次得点H ′,使O ′H ′=2 |OH|。


圆锥侧面展开的示意图[适用章节]数学②中1.1.6柱、锥、台和球的表面积[使用目的]使学生直观的了解圆锥侧面展开的过程,理解底面周长和展开弧长的对应关系和有关的公式。
[操作说明]用课件界面上的“说明”按钮或拖动红色标尺可以了解使用说明。
“展开”、“还原”两个按钮可以显示、还原侧面展开的过程,按钮“闪动”可以交替闪动对应的弧长,“1”、“2”、“关”可以使闪动定格或关闭。
按钮“台”可以帮助理解圆锥和圆台侧面展开图的关系。
(按钮“说明”和“台”没有画出)图2117图2117中是展开后闪动弧长的情况。
拖动标尺到星号及五星处可以看到有关结论,按钮“关”可以隐去这些内容。
活动目的:教育学生懂得“水”这一宝贵资源对于我们来说是极为珍贵的,每个人都要保护它,做到节约每一滴水,造福子孙万代。
活动过程:1.主持人上场,神秘地说:“我让大家猜个谜语,你们愿意吗?”大家回答:“愿意!”主持人口述谜语:“双手抓不起,一刀劈不开,煮饭和洗衣,都要请它来。
”主持人问:“谁知道这是什么?”生答:“水!”一生戴上水的头饰上场说:“我就是同学们猜到的水。
听大家说,我的用处可大了,是真的吗?”主持人:我宣布:“水”是万物之源主题班会现在开始。
水说:“同学们,你们知道我有多重要吗?”齐答:“知道。
”甲:如果没有水,我们人类就无法生存。
小熊说:我们动物可喜欢你了,没有水我们会死掉的。
花说:我们花草树木更喜欢和你做朋友,没有水,我们早就枯死了,就不能为美化环境做贡献了。
主持人:下面请听快板《水的用处真叫大》竹板一敲来说话,水的用处真叫大;洗衣服,洗碗筷,洗脸洗手又洗脚,煮饭洗菜又沏茶,生活处处离不开它。
栽小树,种庄稼,农民伯伯把它夸;鱼儿河马大对虾,日日夜夜不离它;采煤发电要靠它,京城美化更要它。
主持人:同学们,听完了这个快板,你们说水的用处大不大?甲说:看了他们的快板表演,我知道日常生活种离不了水。
乙说:看了表演后,我知道水对庄稼、植物是非常重要的。
