几何画板-立方体展开

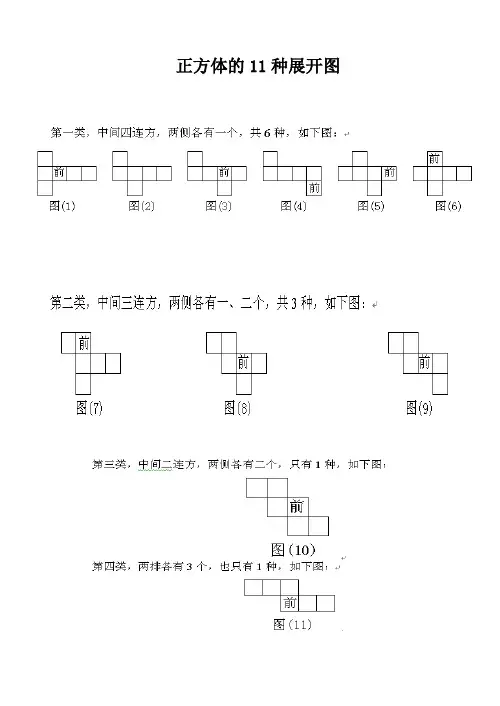
正方体的11种展开图
判断技巧
我们知道，同一个立方体图形，按不同的方式展开得到的平面展开图形一般是不一样的。

常见的正方体平面展开图究竟有几种不同的形状呢？
同学们一定熟悉这样一种操作：把一个正方形纸片平均分成9个小正方形，剪去角上四个小正方形，可以拼成一个无盖的正方体纸盒，其中五个面按习惯不妨记为下、左、右、前、后，如图一。

好啦！现在只要把刚才剪去的一个小正方形作为“上”面，就可拼成一个正方体。

作为正方体平面展开图，这个“上”应该和图1（1）中哪个面拼接在一起呢？观察图1（2），知“上”和前、后、左、右任一个面拼接都行（这四种拼接看作同一种情形），不妨和“后”拼接在一起，如图2。

根据上和下、左和右、前和后相间隔这一规律，现在我们把图2中的“左”或“右”平移，可得图3～图7五种情形。

平移图2中的“前”，可得图8；再平移图8中的“左”，可得图9、图10；把图10中的“上”向左平移，得图11；若移动图8（或图9、图10）中的“左”，又可得图12。

同学们，当你和我一样，把图2～图12这11个图剪下来，动手折一折，得到11个漂亮的小正方体时，你一定为我们的收获感到欢欣鼓舞吧！
对正方体表面展开图的11种情况，为加深记忆，可编成如下口诀：一四一呈6种，一三二有3种，二二二与三三各1种，展开图共有11种。

“动手实践，自主探索和合作交流”是新课程标准倡导学习数学的三种重要方法，而实践活动是培养我们进行主动探索与合作交流的重要途径。

只要通过自己主动观察、实验、猜想、验证等数学活动，就能使我们“建立空间观念，发展几何直觉”，提高思维能力。

湛江师范学院数计院实验报告2011 年级数学与应用数学专业 4 班学号2011224402实验者：刘奇一、实验课题立方体的面的展开与还原二、实验要求将一个立方体的每个面依次展开到一个平面上，再将各面还原成立方体。

三、实验步骤1）定义坐标系，并隐藏网格；在X轴上构造一点，并与原点构造一条线段AB；将这根线段旋转45°，再在这根旋转后的线段上构造一点C，接着将这点与原点构造一条线段AC，然后把刚才旋转后得到的线段隐藏；将线段AB标记向量，然后将线段AC平移得到AC’；在点C和点C’间构造一条线段CC’。

得下图：2）在Y轴上构造一点D，并与原点A构造一条线段AD，然后将线段AD标记线段，接着将平行四边形ABCC’平移得到平行四边形A’B’C’’D’；依次将点B和B’，C和C’，C’和C’’构造线段得到BB’，CC’，C’C’’；将线段AC，CC’，C’C’’设置成虚线。

得下图：3）在线段C’C’’上构造平行线l ；以点C’为圆心，线段C’D为半径作圆，与直线l相交得E点；将该圆隐藏，并在C’DE上构造圆上的弧，在这弧上构造弧上的点F，在点C’和F间作线段C’F；将线段C’C标记向量，把线段C’F平移得到线段CF’，在点F和F’间作线段FF’；点击点F接着点击点E，然后添加移动按钮使F移到E，命名为“移动F→E”；同样的添加一个移动按钮使F移到D。

得下图：4）同上一步的方法，依次将面DB’C’’C’，ABC’C，BB’C’’C’展开得下图：5）以C’’为起点沿C’’K作射线；以K为圆心，DB’为半径作圆，与射线交于O点；将角C’C’’B’标记角度，然后将点O旋转得点O’，并在OKO’上构造圆上的弧，在这条弧上构造一点P，作线段KP；再按前面的方法作出面KPP’K’；最后添加移动按钮。

得下图：6）将按钮归类做系列按钮，命名为“展开”和“还原”；将不必要的线段等隐藏。

得最终图：四、实验反思玩几何画板就是要细心，有耐心！。