近世代数 第23讲

近世代数知识点近世代数知识点第一章基本概念1.1集合●A的全体子集所组成的集合称为A的幂集，记作2A.1.2映射●证明映射：●单射：元不同，像不同；或者像相同，元相同。

●满射：像集合中每个元素都有原像。

Remark：映射满足结合律！1.3卡氏积与代数运算●{（a,b）∣a∈A,b∈B }此集合称为卡氏积，其中（a,b）为有序元素对，所以一般A*B不等于B*A.●集合到自身的代数运算称为此集合上的代数运算。

1.4等价关系与集合的分类★等价关系：1 自反性：∀a∈A,a a;2 对称性：∀a,b∈R, a b=>b a∈R;3 传递性：∀a,b,c∈R,a b,b c =>a c∈R.Remark：对称+传递≠自反★一个等价关系决定一个分类，反之，一个分类决定一个等价关系★不同的等价类互不相交，一般等价类用[a]表示。

第二章群2.1 半群1.半群=代数运算+结合律，记作（S,）Remark: i.证明代数运算：任意选取集合中的两个元素，让两元素间做此运算，观察运算后的结果是否还在定义的集合中。

ii.若半群中的元素可交换，即a b=b a,则称为交换半群。

2.单位元i.半群中左右单位元不一定都存在，即使存在也可能不唯一，甚至可能都不存在；若都存在，则左单位元=右单位元=单位元。

ii.单位元具有唯一性，且在交换半群中：左单位元=右单位元=单位元。

iii.在有单位元的半群中，规定a0=e.3.逆元i.在有单位元e的半群中，存在b,使得ab=ba=e,则a为可逆元。

ii.逆元具有唯一性，记作a-1且在交换半群中，左逆元=右逆元=可逆元。

iii.若一个元素a既有左逆元a1，又有右逆元a2，则a1=a2,且为a的逆元。

4.子半群i.设S是半群，≠T S,若T对S的运算做成半群，则T为S的一个子半群ii.T是S的子半群a,b T,有ab T2.2 群1．群=半群+单位元+逆元=代数运算+结合律+单位元+逆元Remark：i. 若代数运算满足交换律，则称为交换群或Abel群.ii. 加群=代数运算为加法+交换群iii.单位根群Um={m=1},数域P上全体n阶可逆（满秩）矩阵集合GL(n,P),数域P上全体n阶的行列式为1的矩阵集合SL(n,p).2. 群=代数运算+结合律+左（右）单位元+左（右）逆元=代数运算+结合律+单位元+逆元=代数运算+结合律+∀a,b G,ax=b,ya=b有解3. 群的性质i. 群满足左右消去律ii.设G是群，则∀a,b G,ax=b,ya=b在G中有唯一解iii.e是G单位元⇔ e2=eiv.若G是有限半群，满足左右消去律，则G是一个群4. 群的阶群G的阶，即群G中的元素个数，用表示。

子群的指数和拉格朗日定理 当 G 是有限群时, 则子群的阶数与指数也都是有限的, 它们有 以下关系: 定理 2(拉格朗日(Lagrange)) 设G是有限群, H ≤ G, 则 |G| = |H| [G : H]. 由拉格朗日定理立即可得如下推论: (1) 设 G 是有限群, H ≤ G, 则 |H| | |G|. (2) 当 |G|<∞时, 对任何 a∈G 有 o(a) | |G|. (3) 若 |G|= p (素数), 则 G是p 阶循环群, 即素数阶群必为循环群.
子群的指数和拉格朗日定理 关于群中两个有限子群的乘积的元素个数有以下定理. 定理 3 设 G 是群, A, B 是 G 的两个有限子群,则有
| AB |= | A || B | . | A∩ B |
子群的指数和拉格朗日定理 我们可利用拉格朗日定理来确定一个群内可能存在的子群、 元素的阶等, 从而搞清一个群的结构. 以前我们在确定一个群 内的子群时,主要利用元素的生 成子群. 有了拉格朗日定 理, 则首先可由 |G| 的因子来确定可能存在的子群的阶数或元 素的阶数,然后根据子群的阶数来寻找子群. 例 4 确定 S3 中的所有子群. 解 因 |S3|=6, 除平凡子群外, S3中只可能有 2 阶或3 阶子群, 又 因 2 与 3 都是素数, 因而它们都是循环子群, 由 2 阶元和 3 阶 元生成. 故 S3 中全部子群为: H1=1, H2=〈(12)〉, H3=〈(13)〉, H4=〈(23)〉, H5=〈(123)〉, H6=S3.
子群的陪集
陪集有以下性质: (1) aH=H ⇔ a∈H. (2) b∈aH ⇔ aH=bH. 这说明陪集中任何一个元素都可作为代表元. . (3) 两个陪集相等的条件: aH=bH ⇔ a −1b∈H, (Ha=Hb ⇔ ba −1∈H). (4) 对任何 a,b∈G 有 aH=bH 或 aH ∩ bH= ∅. 因而 H 的所有左陪集的集合 {aH | a∈G} 构成 G 的一个划分. 这是因为如果 aH∩bH ≠ ∅, 则存在 x∈aH∩bH, 于是 x=ah1=bh2, 得a −1b=h1h2−1∈H, 由性质(3) 得 aH=bH, 又

3.推移律：
a bb a
a a,不管a是A的哪一个元。
a b, b c a c
定义：若把一个集合A分成若干个叫做类的子集，使得A的每一个元属于而 且只属于一个类，那么这些类的全体叫做集合A的一个分类。
定理1：集合A的一个分类决定A的元间的一个等价关系。
定理2：集合A 的元间的一个等价关系决定A的一个分类。
III.
，方程 和
在G中都有解。
例1 G＝{g}，乘法规定gg=g， 则G是一个群。
例2 G＝{全体整数}；G中运算为普通加法，则G是一个群。
例3 G＝{所有非整数}，G对于普通乘法不作成一个群。
定义1 同态：S , 与 T , 为两个代数系
统, ：S T 为同态映射，若对 a ，b S
有:a b＝ab
S , 定义2 同态满射： 与 为两个代数系统 ，
该映射为同态满射， ，
：S T
T , 为同态映射，且为满射，则 同态
S , T ,
定理1 假定，对于代数运算 和 来说， S与T 同态则：
二元代数运算“
”适合结合律和交换律
则 ai S,i 1,2,n, n个元素
a , a ,, a 1 2
n 的乘积仅与这n个元素
有关而与它们的次序无关。
例 仅满足结合律而不满足交换律：
1）矩阵乘法 2）映射的复合运算 3）字符串的复合运算 同时满足结合律与交换律：
1）普通乘法 2）集合的并、交 3）逻辑与、逻辑或 两者均不满足：
[本章主要内容]
1）群、子群及相关性质； 2）置换群、循环群； 3）子群的陪集、正规子群； 4）群的同态；
2.1半群与群的概念
定义1 设“
”时非空集合S上的一个二元

近世代数知识点近世代数，又称抽象代数，是数学的一个重要分支，它为许多其他数学领域提供了基础和工具。

下面让我们一起来了解一些近世代数的关键知识点。

首先是群的概念。

群是近世代数中最基本的结构之一。

简单来说，一个群就是一个集合 G 以及定义在这个集合上的一种运算“”，满足一些特定的条件。

比如，对于集合中的任意两个元素 a 和 b，运算的结果ab 仍然属于这个集合；存在一个单位元 e，使得对于任意元素 a，都有ae ＝ ea ＝ a；对于每个元素 a，都存在一个逆元 a^（－1)，使得 aa^（－1) ＝ a^（－1)a ＝ e。

群的例子在生活中也有不少，比如整数集合在加法运算下构成一个群。

环也是近世代数中的重要概念。

一个环 R 是一个集合，上面定义了两种运算：加法“＋”和乘法“·”。

加法满足交换律、结合律，有零元，每个元素都有相反数；乘法满足结合律；乘法对加法满足分配律。

常见的环有整数环、多项式环等。

接下来是域。

域是一种特殊的环，它要求非零元素对于乘法运算构成一个群。

比如有理数域、实数域和复数域。

同态和同构是近世代数中用来比较不同代数结构的重要工具。

同态是指两个代数结构之间存在一种保持运算的映射。

如果这个映射还是一一对应的，那就是同构。

同构的两个代数结构在本质上可以看作是相同的。

在近世代数中，子群、子环和理想也具有重要地位。

子群是群的一个子集，在原来的运算下也构成群；子环是环的一个子集，在原来的两种运算下也构成环；理想则是环中的一个特殊子集，对于环中的乘法和加法有特定的性质。

再来说说商群和商环。

以商群为例，给定一个群 G 和它的一个正规子群N，就可以构造出商群G/N。

商群中的元素是由N 的陪集构成的。

近世代数中的重要定理也不少。

比如拉格朗日定理，它对于理解群的结构和性质非常有帮助。

该定理指出，子群的阶整除群的阶。

最后，我们谈谈近世代数的应用。

在密码学中，群和环的理论被广泛用于加密和解密算法的设计。

例 4 设 K4 {e, a, b, c} ,我们可以利用 下表来定义 K4 上的乘法“ ”:
· eabc e eabc aaecb bb c e a c cba e

11
CHENLI
§1 代数运算
定义 1.2 设“ ”是非空集合 A 上的一个代数 运算.
意一个二元运算,并将其称为乘法.当 ab c
时, c 称为 a 与 b 的乘积;甚至还将等式 ab c
简写成 ab c .

6
CHENLI
§1 代数运算
例 1 设 R 是实数集.于是,平常的加法“”,减 法“-”和乘法“”都是 R 上的二元运算;除法“”是 R , R \{0}到 R 的代数运算,不是 R 上的二元运算.
明:在不改变元素顺序的前提下,无论怎样在其中添
加括号其中添加括号,这 n 个元素的乘积总等于
n
ai ，
i 1
从而与加括号的方式无关.

23
CHENLI
§1 代数运算
事实上,当 n 1或 n 2 时,无需加括号,我们的结论
自然成立.当 n 3时,由于“ ”适合结合律,我们的结论成

17
CHENLI
§1 代数运算
但是,当“ ”适合结合律时,我们可以定义 A 中任意有限 n ( n 3 )个元素 a1, a2 , , an 的乘积 a1a2 an .这是因为,容易证明,对于 A 中任意 n 个元素 a1, a2 , , an ,只要不改变它们的次序,运 算结果与加括号的方式无关(见习题 2).这样一 来,我们便可定义 a1, a2 , , an 的乘积 a1a2 an 就 是按任意一种方式添加括号后的算出的结果.

2
CHENLI

域是近世代数中的一个基本概念，它是一个加法群和 一个乘法半群的组合，具有一些重要的性质。
详细描述
域是一个非空集合，其中定义了两种运算：加法和乘法 ，满足一定的性质。在域中，加法和乘法都是可逆的， 即每个元素都有唯一的加法逆元和乘法逆元。此外，域 中的乘法满足结合律，且每个元素都有乘法单位元。
子域与扩域
环论在几何学中的应用
环论也是近世代数的一个重要分支，它在几何学中也有着广泛的应用。例如，在代数几 何中，环论被用于描述多项式环的结构；在解析几何中，环论也被用于描述函数的性质。
数论中的应用
域论在数论中的应用
域论是近世代数中一个重要的分支，它在数论中有着广泛的应用。例如，在代数数论中，域论被用于描述代数数 的性质；在数论中，域论也被用于研究整数的性质和结构。
分式域与函数域
总结词
分式域和函数域是两种特殊的域，它们在数学和物理 中有广泛的应用。分式域是由其整环的分式组成的域 ，而函数域则是基于函数的定义域和值域形成的域。
详细描述
分式域是由一个整环的分式组成的域。整环是一个只含 有限除数的环，也就是说，如果一个元素在整环中不能 被其他元素整除，则该元素被称为不可约元素。分式环 是由整环中所有分式组成的集合，它构成一个域。函数 域是基于函数的定义域和值域形成的域。具体来说，给 定一个函数f和一个集合D，函数域是由集合D中所有可 能的函数值组成的集合，它也构成一个域。
交叉学科的研究
近世代数与其他学科的交叉研究也是未来的一个重要方向，如 代数几何、代数数论、计算机科学等学科的交叉研究，可以促
进近世代数的发展和应用。
THANKS
感谢观看
环论
环的定义和性质
要点一
总结词
环是具有加法和乘法两种运算的代数系统，满足一定的性 质。

近 世 代 数 课 堂 讲 义 整 理 V 1.2
但是 A ∪ B 不一定。 【定义】由包含 A 的所有子半群的交集 Q 称作由 A 生成的子半群，记作 ( A) 。
∩ (A) =
P 即 ( A) 为所有包含 A 的子半群的交。
P⊇A P为S的子半群
理想：
设 (S, ) 为半群， A ⊆ S, A ≠ ∅ ，若 SA ⊆ A ，则 A 为 S 的左理想；若 AS ⊆ A ，则 A 为 S
4.循环群的子群 ①循环群的子群是循环群； ②子群的个数及生成元：
子群的阶能整除群的阶，所以子群的个数为 n 的因子数。 设 G 是循环群，| G |= n ，它的子群为 H ，| H |= (am ) ，则 m | n 。
③若 n 有因子 q ，则 G 必有 q 阶子群；（这个结论对有限交换群（有限阿贝尔群）成立，对
同态（映射）。
【定理】 设 (S, ) 为半群， (T ,∗) 为代数系，若存在满射 ϕ : S → T ，且 ∀x, y ∈ S ，有 ϕ(x y) = ϕ(x) ∗ϕ( y) ，则 (T ,∗) 为半群。 若 (S, ) 为幺半群，条件同上，可以推出 (T ,∗) 为幺半群。
第 3 页共 12 页
3.生成元
第 5 页共 12 页近源自世 代 数 课 堂 讲 义 整 理 V 1.2
⑤ G = (a) ，| G |=| a |= n ，G = (am ) ⇒ m 、n 互质，这个群的生成元有φ(n) 个，其中φ(n) 为欧拉函数，为小于或等于 n 且与 n 互素的正整数个数； ⑥ G = (a) ，| G |=| a |= ∞ ，生成元只有 a 、 a−1 。
ϕ =ϕ γ
其中 γ 为 M 到 M Eϕ 的自然同态； ④ 如果ϕ 是满同态，则 M Eϕ 与 M ' 同构。

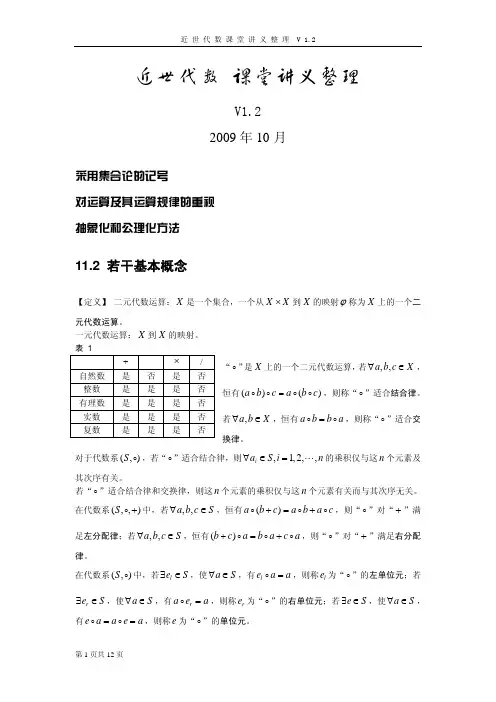
近世代数知识点第一章基本概念1.1 集合A 的全体子集所组成的集合称为A 的幂集，记作2 A.1.2 映射证明映射：单射：元不同，像不同；或者像相同，元相同。

满射：像集合中每个元素都有原像。

Remark ：映射满足结合律！1.3 卡氏积与代数运算{ (a,b ) la € A,b € B }此集合称为卡氏积，其中(a,b )为有序元素对，所以一般A*B不等于B*A.集合到自身的代数运算称为此集合上的代数运算。

1.4 等价关系与集合的分类★等价关系： 1 自反性：? a€ A,a~a;2 对称性：? a,b€ R, a~b=>b ~a€R;3 传递性：? a,b,c€ R,a~b,b ~c =>a ~c€ R.Remark :对称+传递工自反★一个等价关系决定一个分类，反之，一个分类决定一个等价关系★不同的等价类互不相交，一般等价类用[a] 表示。

第二章群2.1 半群1. 半群=代数运算+结合律，记作（S,°）Remark: i. 证明代数运算：任意选取集合中的两个元素，让两元素间做此运算，观察运算后的结果是否还在定义的集合中。

ii. 若半群中的元素可交换，即a°b=b °a, 则称为交换半群。

2. 单位元i. 半群中左右单位元不一定都存在，即使存在也可能不唯一，甚至可能都不存在；若都存在，则左单位元=右单位元=单位元。

ii. 单位元具有唯一性，且在交换半群中：左单位元= 右单位元= 单位元。

iii. 在有单位元的半群中，规定a0=e.3. 逆元i. 在有单位元e 的半群中，存在b, 使得ab=ba=e, 则a 为可逆元。

ii. 逆元具有唯一性，记作a-1且在交换半群中，左逆元=右逆元= 可逆元。

iii. 若一个元素a既有左逆元al,又有右逆元a2,则a1=a2,且为a的逆元。

4. 子半群i. 设S是半群，？ T?S若T对S的运算做成半群，贝U T为S的一个子半群ii. T是S的子半群？？a,b ET,有ab ET2.2 群1．群=半群+单位元+逆元=代数运算+结合律+单位元+逆元Remark ：i. 若代数运算满足交换律，则称为交换群或Abel 群.ii. 加群=代数运算为加法+ 交换群iii. 单位根群Um={ ??€??|?叨=1},数域P上全体n阶可逆（满秩）矩阵集合GL（n,P）,数域P上全体n阶的行列式为1的矩阵集合SL（n,p）.2. 群=代数运算+结合律+左（右）单位元+左（右）逆元=代数运算+结合律+ 单位元+逆元=代数运算+结合律+ ? a,b €G,ax=b,ya=b 有解3. 群的性质i. 群满足左右消去律ii. 设G是群，则？ a,b €G,ax=b,ya=b 在G中有唯一解iii. e 是G 单位元? e2=eiv. 若G是有限半群，满足左右消去律，则G是一个群4. 群的阶群G的阶，即群G中的元素个数，用|??表示。

• 假如运算1和1‘来说，有一个A到A’的满射的同态映射存在，同态满射 • 同构映射 一一映射的同态映射就是一个同构映射 • 自同构
第8页/共27页
等价关系与等价类
• 集合的等价关系 。Ⅱ，
对称律:a～b＝>b～a Ⅲ，推移律：a～b，b～c=>a～c 同余关系
第22页/共27页
除环、域
• 除环 1， R至少包含一个而不等于零的元
的每一个不等于零的元有一个逆元
2，R有单位元
3，R
• 域 一个交换除环叫做一个域
• 在一个没有零因子的环里所有不等于零的元对于加法来说的阶都一样的
• 一个无零因子的环里的非零元的相同的阶叫做环的特征
• 整环 除环 域 的特征或是无限大 或是一个素数
（b+c）a=ba+ca
第21页/共27页
交换律、单位元、零因子、整环
• 交换环 一个环 假如 ab=ba不管a b是环的哪两个元 • 单位元 ea=ae=a 一个环未必有单位元 • 零因子 若环里a≠0，b≠0但 ab=0 那么 a是左零因子 b 右零因子 • 整环 一个环叫做整环 如果 1.乘法适合交换律：ab=ba 2 .R有单位元1：1a=a1=a 3 R没有零因子ab=0=>a=0或b=0
合D的一个映射
像 逆象，
• 映射的相同 效果相同就行
第5页/共27页
代数运算
• 定义一个A×B到D的映射叫做一个A×B到D的代数运算 • 代数运算是一种特殊的映射 描写它的符号，也可以特殊一点，一个代数运算我们用。来
表示 • 二元运算 假如。是一个A×A到A的代数运算，我们说集合A是闭的 二元运算
换群 • 定理2 一个集合的所有一一变换做成一个变换群 • 定理3 任何一个群都同一个变换群同构 证明，假定G是一个群，G的元是a，b，c ·······我们在G里任意取出一个元x来，那么‫ג‬x：

A1 , A2 ,, An
和
A1 A2 An 我们有
A1 A2 An
( x A1 A2 A) ( x至少属于某一Ai , i 1, 2,, n)
( x A1 A2 A) ( x属于每一Ai , i 1, 2,, n)
全体复数的集合，表示为C
设A，B是两个集合，如果A 的每一元素都是B 的
元素，那么就说Ａ是Ｂ的子集，记作 作 ，或记
. 根据这个定义，Ａ是Ｂ的的子集当且仅当
A B
.
BA 对于每一个元素 x，如果
，就有
x A
A是B的子集，记作：
xB
( A B) (x : x A x B)
f :x y
这时y 叫做 x 在f 之下的象，记作 . f (x )
例1 设
A B {1,2,3,4}
这是A到B的一个映射.
f : 1 2,2 3,3 4,4 1
例2 设A是一切非负数的集合，B是一切实数的集合. 对于每 一 与它对应. f 不是A到B的映射， x ，令 A f ( x) x 因为当 时， 不能由x唯一确定.
设 f :AB 如果对于每一 x A 与g是相等的. 记作
，B g:A ，都有
f ( x) g ( x)
都是A到B的映射， ，那么就说映射f
f g
例3
令
f : R R, x | x |
2 g : R R , x x 那么 .
f g
定义4： 设 是A到B 的一个映射， g : B C f :AB 是B 到C 的一个映射. 那么对于每一个 ， x A g ( f ( x)) 是C中的一个元素. 因此，对于每一 ，就有C 中唯一的确定 x A 的元素 与它对应，这样就得到A到C 的一个映射，这映 g ( f ( x和 )) 射是由 所决定的，称为 f 与g 的合成（乘积），记作 f : A . B 于是有 g:BC

2019/1/20
数学上的确切描述
设由m颗珠子做成一个项链，可用一个正m边形 来代表它，它的每个顶点代表一颗珠子。
沿逆时针方向给珠子标号， 由于每一颗珠子的颜色有n种选 择，因而用乘法原理，这些有标 号的项链共有nm种。
但其中有一些可以通过旋转一个角 度或翻转180度使它们完全重合， 我们称为是本质相同的，我们要考 虑的是无论怎么旋转、翻转都不能 使它们重合的项链类型数。
2019/1/20
例5 简单检错码—奇偶性检错码
设用6位二进制码来表示26个英文字母，其中 前5位顺序表示字母，第6位做检错用，当前5位的 数码中1的个数为奇数时，第6位取1，否则第6位 是0。这样编出的码中1的个数始终是偶数个。例 如， A：000011 B：000101 C：000110 D：001001 …… 用这种码传递信息时可检查错误。当接收方收到的 码中含有奇数个1时，则可断定该信息是错的，可 要求发送者重发。因而，同样的设备，用这种编码 方法可提高通信的准确度。
2019/1/20
6. 数字通信的可靠性问题 现代通信中用数字代表信息，用电子设 备进行发送、传递和接收，并用计算机加以 处理。由于信息量大，在通信过程中难免会 出现错误。为了减少错误，除了改进设备 外，还可以从信息的表示方法上想办法。用 数字表示信息的方法称为编码。编码学就是 一 门 研 究 高 效 编 码 方 法 的 学 科 。 下面用两个简单的例子来说明检错码与 纠错码的概念。
2019/1/20
伽利略死后，直到19世纪末期，他的理 论才由别的数学家加以进一步的发展和系统 的阐述。 这样一门具有悠久历史、充满许多有趣 问题和故事的数学分支，在近代又得到了蓬 勃发展和广发应用，出现了许多应用与某一 领域的专著，正吸引越来越多的科技人员和 学生来学习和掌握它。

例2 设 A 1 { 东} ， A 2 { 西 南 } ， B { 高} ，低
则 1 :A 1 A 2 B ; ( 西 , 南 ） 高 不是映射.
因为映射要满足每一个元 (a1,a2) 都要有一个像．
而 2 : A 1 A 2 B ; ( 西 , 南 ） 高 ； ( 东 , 南 ） 低 是一个映射． 7
A 1A 2 A n{a1 (,a2, an)ai A i}.
即由一切从 A1,A2, ,An 里顺序取出元素组成的元素 组 (a1,a2, an)，ai Ai 组成的集合．
例 A={1,2,3}， B={4,5}, 则
AB={(1,4), (1,5), (2,4), (2,5), (3,4), (3,5)}，
A称为 的定义域，B称为 的值域.
注: (1) 映射定义中 “b”的唯一性：映射不能“一对多”，
但可以“多对一”．
(2) 记法： ：A B ;ab (a )，aA ．
(3) 一般情形，将A换成集合 A 1A 2.. .A n 的积，则
对 ( a 1 ,a 2 ,.a n .) .A ,1 A 2 . .A .n有 : A 1 A 2 . . . A n B ; ( a 1 , a 2 , . . . , a n ) b ( a 1 , a 2 , . . . , a n ) . 6
2. 元素（或元）: 组成一个集合的事物.
如果a是集合A中的元素，记作a A ； 如果a不是集合A的元 素，记作 a A 或a A .
2
3．空集：没有元素的集合，记作 .
4．子集：设A,B是集合，则
B A (B是A的子集)是指 b B b A . 真子集：B是A的真子集是指 B A 且 aA，但aB .

2
2
故平面上全体一一变换构成的变换群不是交换群。
定理7.3.3 任意一个群都同构于一个变换群。
证. 设( G, ∗)是群，g ∈ G。
定义变换 Tg: G →G, a→ g∗a 。 [压缩或平移变换]
下面证明 ( T(G ),◦) 是群，其中 T(G ) ={ Tg| g ∈ G }：
若Tg( a) = Tg( b), 则 g∗a = g∗b, 由消去律得 a = b, Tg是单射;
(123), (132), (124), (142), (134), (143), (234), (243);
(1234), (1243), (1324), (1342), (1423), (1432); (12)∘(34), (13)∘(24), (14)∘(23)。
• 注意到 (i1 i2 i3 ⋅⋅⋅ ik ) = (i1 i2)∘(i2 i3)∘⋅⋅⋅∘(ik-1 ik) = (i1 ik)∘(i1 ik-1)∘⋅⋅⋅∘(i1 i2)
)
i2
(i2 )
in (in
)
通常用第一种方式表示置换，等价于将置换看作:
σ : i →j , ( i =1, 2, ⋅⋅⋅ )
例7.3.5 设有限集合S = {a1, a2, a3}，则 S上的每一 个置换可以用六种不同的方式来表示。比如，
τ : a1 → a2 , a2 → a3, a3 → a1 ,
(1
j1
j2 jk )
(k 1)
而置换
(
jk1 n
jk1) (
n)
是个≤n-1元的置换，根据归纳法假设，她可以分解成若干 个不含公共元素的循环置换的乘积。当然，这些循环置换
都可以看作n个元素的循环置换。因此，τ 就分解成若干个

第23讲§1 0 商 域大家都熟悉的例子:Z (整数环)是满足上述条件的环, 利用Z 中的元素要 “构造”出一个域——有理数域. 由此方法,本讲推出了商域的概念和由无零因子环构 造商域的方法。

一、主要定理定理3.1 0 .1. 设R 是无零因子的交换环,则存在一个 域Q ,使R 成为Q 的一个子环。

证: 情形1.若R 是零环,则任取一个域Q 且令{}0=R 是Q的零理想,那么必有R R ≅,由挖补定理知必存在Q 为环使Q R ⊆ 且 Q Q ≅ ∴Q 为域.情形2，若{}0≠R ，（参照p99例4） （1）构造一个集合：(){}∙⨯=≠∈=R R b R b a b a A 0,,且。

{}0≠R ∅≠⇒A 。

（2）在A 中定义关系“～”：()b a ,～()bc ad d c =⇔,。

可以验证“～”是A 的一个等价关系，事实上， (ⅰ) (),,a b A ab ba ∀∈=()b a ,⇒ ～()b a ,，(比较p91.(i)。

) (ⅱ) 若()b a ,～()()d c da cb bc ad d c ,,⇒=⇒=⇒～()b a ,. (ⅲ) 若 ()b a ,～()d c , 且 ()d c ,～(),e f ad bc ⇒=且cf de adf bcf=⇒=且.bcf bde afd bed =⇒= （R d ,0≠中无零因子⇒有消去律）()b a be af ,⇒=⇒～(),e f , 由(ⅰ)、(ⅱ)和(ⅲ)知“～”是一个等价关系。

（3）利用A 上的等价关系“～”,可在A 中进行分类(),,A b a ∈∀ 则()b a ,所在的类记为⎥⎦⎤⎢⎣⎡b a 。

(仅是记号)则可作集合 ⎭⎬⎫⎩⎨⎧∈∀⎥⎦⎤⎢⎣⎡=A b a b a Q ,|0， （4）现在0Q 中定义运算 加法:⎥⎦⎤⎢⎣⎡+=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡bd bc ad d c b a ，乘法: ⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡bd ac d c b a , 须证上述定义的合理性:(ⅰ) 当()b a ,,()0,≠⇒∈b A d c 且0≠d , 而R 无零因子0≠⇒bd,∴()A bd bc ad ∈+,且 ()A bd ac ∈,,于是0Q bd bc ad ∈⎥⎦⎤⎢⎣⎡+且0Q bd ac ∈⎥⎦⎤⎢⎣⎡ (ⅱ) 运算与类的代表元无关. 事实上,若⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡''b a b a , 且''''ba ab d c d c =⇒⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡''dc cd = 首先, ''''dd ba dd ab =且⇒=''''bb dc bb cd⇒+=+''''''''b bdc d bda d cbb d adb()()⇒+=+bd b c d a d b cb ad '''''' ()bd cb ad ,+～()⇒+'''''',d b b c d a⎥⎦⎤⎢⎣⎡+=⎥⎦⎤⎢⎣⎡+''''''d b b c d a bd cb ad 即⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡''''d c b a d c b a 其次, ,''''cd ba cd ab = ⇒=''''dc ba cd ba ''''c bda d acb =即 ()bd ac ,～()⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⇒'''''''',d b c a bd ac d b c a .所以⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡''''d c b a d c b a 由上证明知，如上定义的加法和乘法是合理的。

《近世代数》课程教案第一章 基本概念教学目的与教学要求:掌握集合元素、子集、真子集。

集合的交、并、积概念;掌握映射的定义及应注意的几点问题，象，原象的定义;理解映射的相同的定义;掌握代数运算的应用；掌握代数运算的一般结合运算，理解几个元素作代数运算的特点；理解代数运算的结合律；掌握并能应用分配律与结合律的综合应用；掌握满射,单射,一一映射及逆映射的定义。

理解满射，单射，一一映射及逆映射的定义；掌握同态映射、同态满射的定义及应用;掌握同构映射与自同构的定义;掌握等价关系的定义，理解模ｎ的剩余类。

教学重点:映射的定义及象与原象的定义，映射相同的定义;代数运算的应用，对代数运算的理解;代数运算的结合律;对定理的理解与证明;同态映射,同态映射的定义；同构映射的定义以及在比较集合时的效果；等价关系,模n 的剩余类。

教学难点：元素与集合的关系(属于)，集合与集合的关系（包含）;映射定义,应用该定义应注意几点；代数运算符号与映射合成运算符号的区别；结合率的推广及满足结合律的代数运算的定义；两种分配律与⊕的结合律的综合应用;满射，单射，一一映射及逆映射的定义;同态映射在比较两个集合时的结果;模n 的剩余类。

教学措施：网络远程。

教学时数:8学时。

教学过程:§1 集合定义：若干个(有限或无限多个)固定事物的全体叫做一个集合（简称集）。

集合中的每个事物叫做这个集合的元素（简称元）。

定义:一个没有元素的集合叫做空集,记为∅，且∅是任一集合的子集。

(1)集合的要素：确定性、相异性、无序性。

(2)集合表示:习惯上用大写拉丁字母A ,B ,C …表示集合,习惯上用小写拉丁字母a ，b ,c …表示集合中的元素。

若ａ是集合A 中的元素,则记为A a A a ∉∈否则记为,。

表示集合通常有三种方法： 1、枚举法（列举法)： 例：A ＝{1，２，3,4｝，B =｛１，2，３,…，100}。

2、描述法:{})(,)(x p x p x A =—元素x 具有的性质。