圆柱和圆锥的整理与复习

六年级下册数学教案及教学反思2.9 圆柱与圆锥整理和复习丨苏教版教案：六年级下册数学——2.9 圆柱与圆锥整理和复习作为一名经验丰富的教师，我始终坚信复习是学习过程中的重要环节。

本节课，我将带领学生对苏教版六年级下册的2.9圆柱与圆锥进行整理和复习，帮助他们在巩固知识的同时，提高解决问题的能力。

一、教学内容1. 圆柱的特征与性质，包括圆柱的底面、高、侧面积和体积的计算方法。

2. 圆锥的特征与性质，包括圆锥的底面、高、侧面积和体积的计算方法。

3. 圆柱与圆锥在实际问题中的应用，例如计算物体体积、制作几何模型等。

二、教学目标1. 使学生掌握圆柱与圆锥的基本概念、特征和计算方法。

2. 培养学生运用圆柱与圆锥知识解决实际问题的能力。

3. 提高学生的数学思维能力和团队协作能力。

三、教学难点与重点1. 教学难点：圆柱与圆锥体积计算公式的灵活运用，以及实际问题中的变形运用。

2. 教学重点：圆柱与圆锥的基本概念、特征和计算方法的巩固。

四、教具与学具准备1. 教具：多媒体课件、圆柱和圆锥模型、黑板、粉笔。

2. 学具：学生手册、练习本、铅笔、橡皮。

五、教学过程1. 实践情景引入：以一个圆柱形的水桶和一个圆锥形的沙堆为例，让学生观察并描述它们的特点。

2. 知识回顾：引导学生复习圆柱与圆锥的基本概念、特征和计算方法。

3. 例题讲解：选取具有代表性的例题，讲解圆柱与圆锥的计算方法及其在实际问题中的应用。

4. 随堂练习：为学生提供一些有关圆柱与圆锥的计算题目，让学生独立完成，并及时给予指导和反馈。

5. 团队协作：将学生分成小组，让他们共同探讨圆柱与圆锥在实际问题中的运用，并选取小组代表进行分享。

六、板书设计板书内容主要包括圆柱与圆锥的基本概念、特征、计算公式及实际应用。

板书设计要简洁明了，突出重点。

七、作业设计（1）圆柱：底面半径为5cm，高为10cm。

（2）圆锥：底面半径为3cm，高为12cm。

2. 答案：（1）圆柱体积：V = πr²h = 3.14 × 5² × 10 = 7850cm³（2）圆锥体积：V = 1/3πr²h = 1/3 × 3.14 × 3² × 12 = 113.04cm³八、课后反思及拓展延伸重点和难点解析：在上述教案中，有几个重点和难点需要特别关注。

完整版)圆柱体和圆锥体知识点复习整理圆柱体和圆锥体知识点复整理
本文档旨在提供关于圆柱体和圆锥体的知识点复整理。

以下是相关的知识点介绍：
圆柱体（Cylinder）
圆柱体是一个由两个平行的圆面和一个定位于两圆面之间的侧面所组成的几何体。

以下是一些圆柱体的重要特征：
底面积：圆柱体底面的面积可以通过圆的面积公式计算。

圆的面积公式为：A = πr²，其中 r 是圆的半径。

侧面积：圆柱体的侧面积可以通过将圆的周长乘以圆柱体的高度来计算。

侧面积公式为：A = 2πrh，其中 h 是圆柱体的高度，r 是圆的半径。

总表面积：圆柱体的总表面积可通过将底面积和侧面积相加来计算。

总表面积公式为：A = 2πr² + 2πrh。

圆锥体（Cone）
圆锥体是一个由一个圆形底面和一个定位于底面圆心的侧面所组成的几何体。

以下是一些圆锥体的重要特征：
底面积：圆锥体底面的面积可以通过圆的面积公式计算。

圆的面积公式为：A = πr²，其中 r 是底面圆的半径。

侧面积：圆锥体的侧面积可以通过将圆的周长乘以圆锥体的斜高来计算。

侧面积公式为：A = πrl，其中 l 是圆锥体的斜高，r 是底面圆的半径。

总表面积：圆锥体的总表面积可通过将底面积和侧面积相加来计算。

总表面积公式为：A = πr² + πrl。

以上是关于圆柱体和圆锥体的知识点复习整理。

希望对您有所帮助！。

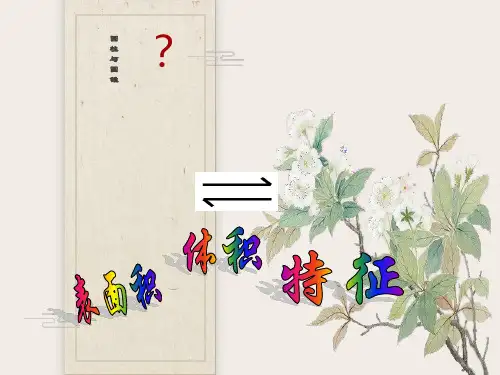
圆柱与圆锥知识点整理六年级一、圆柱的相关计算公式：底面积：S底=πr²底面周长：C底=πd=2πr侧面积：S侧=2πrh表面积：S表=2S底+S侧=2πr²+2πrh体积：V柱=πr²h1.圆柱的切割：①横切：切面是圆，表面积增加2倍底面积，即S增=2πr²②竖切（过直径）：切面是长方形（如果h=2R，切面为正方形），该长方形的长是圆柱的高，宽是圆柱的底面直径，表面积增加两个长方形的面积，即S增=4rh2.圆柱的特征：①底面的特征：圆柱的底面是完全相等的两个圆。

②侧面的特征：圆柱的侧面是一个曲面。

③高的特征：圆柱有无数条高。

3.圆柱的侧面展开图：①沿着高展开，展开图形是长方形，如果h=2πr，则展开图形为正方形②不沿着高展开，展开图形是平行四边形或不规则图形③无论怎么展开都得不到梯形二、圆锥的相关计算公式：底面积：S底=πr²底面周长：C底=πd=2πr体积：V锥=1/3πr²h1.圆锥的切割：①横切：切面是圆②竖切（过顶点和直径直径）：切面是等腰三角形，该等腰三角形的高是圆锥的高，底是圆锥的底面直径，面积增加两个等腰三角形的面积，即S增=2rh2.圆锥的特征：①底面的特征：圆锥的底面一个圆。

②侧面的特征：圆锥的侧面是一个曲面。

③高的特征：圆锥有一条高。

3.圆柱和圆锥的关系①圆柱与圆锥等底等高，圆柱的体积是圆锥的3倍。

②圆柱与圆锥等底等体积，圆锥的高是圆柱的3倍。

③圆柱与圆锥等高等体积，圆锥的底面积（注意：是底面积而不是底面半径）是圆柱的3倍。

④圆柱与圆锥等底等高，体积相差2/3Sh专项练习题一、填空。

1. 把圆柱的侧面沿高剪开，得到一个( )，这个( )的长等于圆柱底面的( )，宽等于圆柱的( )，所以圆柱的侧面积等于( )。

2. 415平方厘米＝( )平方分米 4.5立方米＝( )立方分米2.4立方分米＝( )升( )毫升 4070立方分米＝（）立方米3立方分米40立方厘米＝（）立方厘米325 立方米＝（）立方分米538 升＝（）升（）毫升3. 将4个棱长为1分米的正方体拼成一个长方体，这个长方体的表面积是( )平方分米，体积是( )立方分米。

人教版数学六年级下册《圆柱圆锥整理和复习》教案教案一. 教材分析《圆柱圆锥整理和复习》是人教版数学六年级下册的一章内容。

本章主要让学生掌握圆柱和圆锥的基本概念、特性、计算方法及其应用。

通过本章的学习，学生能够进一步理解和掌握圆柱和圆锥的相关知识，提高解决问题的能力。

二. 学情分析六年级的学生已经具备了一定的空间想象能力和逻辑思维能力，对圆柱和圆锥有一定的了解。

但部分学生可能对一些概念和计算方法的理解不够深入，需要在教学中加以引导和巩固。

三. 教学目标1.知识与技能：理解和掌握圆柱和圆锥的基本概念、特性、计算方法及其应用。

2.过程与方法：通过观察、操作、思考、交流等数学活动，培养学生的空间想象能力和逻辑思维能力。

3.情感态度与价值观：激发学生对数学的兴趣，培养学生的团队合作意识和克服困难的勇气。

四. 教学重难点1.重点：圆柱和圆锥的基本概念、特性、计算方法及其应用。

2.难点：对一些概念和计算方法的理解和运用。

五. 教学方法采用问题驱动法、合作学习法、案例分析法等教学方法，引导学生主动探究、合作交流，提高学生的数学素养。

六. 教学准备1.教具准备：圆柱和圆锥模型、多媒体课件等。

2.学具准备：学生自带圆柱和圆锥模型、练习本等。

七. 教学过程导入（5分钟）教师通过提问方式引导学生回顾圆柱和圆锥的基本概念、特性、计算方法，为新课的学习做好铺垫。

呈现（10分钟）1.教师通过展示圆柱和圆锥的模型，引导学生观察和描述其特征。

2.教师利用多媒体课件，展示圆柱和圆锥的计算方法及其应用。

操练（10分钟）1.教师给出几个有关圆柱和圆锥的问题，让学生独立解答。

2.学生互相交流解题过程，教师进行点评和指导。

巩固（10分钟）1.教师学生进行小组讨论，探讨如何运用圆柱和圆锥的知识解决实际问题。

2.学生代表分享讨论成果，教师进行点评和指导。

拓展（10分钟）1.教师提出一些有关圆柱和圆锥的拓展问题，引导学生进行思考和探究。

2.学生互相交流解题过程，教师进行点评和指导。

六年级下册数学教案《第3单元圆柱与圆锥整理和复习》人教版一. 教材分析本节课为人教版六年级下册数学第3单元“圆柱与圆锥”的整理和复习。

本单元的主要内容是圆柱和圆锥的特征、体积计算以及应用。

教材通过复习和整理，使学生对圆柱和圆锥的概念、性质、计算方法等有一个清晰、系统的认识，提高学生的空间想象能力和解决问题的能力。

二. 学情分析六年级的学生已经学习了圆柱和圆锥的基本知识，对圆柱和圆锥的特征、体积计算有一定的了解。

但部分学生对一些概念和公式的理解不够深入，应用能力有待提高。

此外，学生的空间想象能力和解决问题的能力参差不齐，需要在教学中加以关注和培养。

三. 教学目标1.知识与技能：通过对圆柱和圆锥的复习，使学生掌握圆柱和圆锥的基本概念、性质和体积计算方法，提高空间想象能力和解决问题的能力。

2.过程与方法：通过自主学习、合作交流、探究发现等方法，培养学生的动手操作能力和思维能力。

3.情感态度与价值观：激发学生学习数学的兴趣，培养学生的创新意识和团队协作精神，使学生感受到数学与生活的密切联系。

四. 教学重难点1.重点：圆柱和圆锥的基本概念、性质和体积计算方法的掌握。

2.难点：对圆柱和圆锥体积公式的理解与应用，以及空间想象能力的培养。

五. 教学方法1.自主学习：引导学生独立思考，自主探究，发现和总结圆柱和圆锥的特点和规律。

2.合作交流：鼓励学生与他人分享学习心得，互相讨论，共同解决问题。

3.探究发现：引导学生动手操作，观察分析，发现圆柱和圆锥的体积计算方法。

4.启发引导：教师通过提问、设疑，引导学生思考，激发学生的学习兴趣。

六. 教学准备1.教具：圆柱和圆锥模型、图片、课件等。

2.学具：学生每人准备一个圆柱和圆锥模型，以及相关计算工具。

七. 教学过程1.导入（5分钟）利用课件展示生活中的圆柱和圆锥物体，引导学生回顾已学的知识，为新课的复习打下基础。

2.呈现（10分钟）教师通过讲解和示范，呈现圆柱和圆锥的基本概念、性质和体积计算方法。

圆柱和圆锥的整理和复习刘杰文教学内容：新人教版六年级数学第37页的整理和复习教学目标：1、引导学生通过回忆、整理、拓展等实践活动，掌握圆柱与圆锥的相关特点与特征，并能熟练地运用公式进行圆柱、圆锥表面积或体积的计算。

2、通过让学生对知道的整理提高学生的自主获取知识与概括知识能力。

在练习、讨论、合作中发展学生的空间观念，并进一步提高运用知识解决实际问题的能力。

3、通过整理、交流、合作、探究、体验探究的乐趣，感受数学的价值，培养学生“学数学、用数学”的意识和创新的精神。

教学重点：掌握圆柱与圆锥的相关特点与特征，并能熟练地运用公式进行圆柱、圆锥表面积或体积的计算。

教学难点：通过对知识进行整理，提高学生的自主获取知识与概括知识能力。

教具准备：多媒体课件教学过程：一、由面到体，揭示课题。

1、把一张长方形的纸贴在木棒上，快速转动，转出来的是什么形状？（板书：圆柱）思考：长方形长、宽与圆柱的分别有什么关系？2、把一张三角形的纸贴在木棒上，快速转动，转出来的是什么形状？（板书：圆锥）引导观察：直角三角形两条直角边与圆锥的有什么关系？3、揭示课题教师：通过第三单元的学习，我们已经认识了圆柱和圆锥。

这节课我们将对本单元的知识进行系统的整理和复习，通过整理和复习进一步加深对圆柱和圆锥特征的认识，能熟练地解决常见的有关圆柱与圆锥的问题。

（板书课题：圆柱、圆锥的整理和复习）二、回顾整理、建构网络。

1、自主整理、实施创造。

（1）自主整理。

学生对本单元的知识进行整理。

课件出示：对圆柱和圆锥的知识点进行梳理要求：1、试着用你所喜欢的方式来整理。

2、整理结果要有条理、层次分明。

3、整理结果要能体现知识间的联系和区别。

4、小组内的同学交流再整理成本组集体知识网络。

（2）展示整理成果，并介绍说明。

一、特征采用列举法整理圆柱和圆锥的特征的：圆柱的特征：⑴圆柱有上下两个底面，两个底面是完全相等的两个圆。

⑵圆柱有一个侧面是曲面。

（学生补充：侧面展开是一个长方形（有时是一个正方形）。

《圆柱和圆锥的整理与复习》教学设计教学内容：六年级下册圆柱和圆锥的整理与复习教学目标：1、回顾本单元的知识内容，进一步认识圆柱、圆锥的特征，巩固圆柱的侧面积、表面积及圆柱和圆锥的体积计算的一般方法，进一步理解直柱体的表面积可以用“两个底面积+侧面积”来计算，直柱体的体积可以用“底面积×高”来计算。

2、能运用有关知识，灵活地解决一些实际问题。

3、让学生体验掌握数学知识的成功喜悦，激发学习的兴趣，培养善于归纳总结、自我激励的良好学习习惯。

教学重点：归纳整理有关圆柱和圆锥的知识，形成知识体系。

教学难点：理解圆柱体与长方体、正方体等表面积及体积之间的联系，理解圆柱和圆锥之间的联系和区别，提高运用知识解决问题的能力。

教学过程：一、梳理知识点1、导入同学们,这节课我们要一起来复习圆柱和圆锥的有关知识。

2、检查课前整理知识情况3、展示交流，复习知识点师：《圆柱与圆锥》这一单元，你学会了哪些知识？谁来汇报一下。

指名学生上台投影交流展示并说出整理过程4、本单元易错点（指名说）二、练习与思考你能计算下面各图形的表面积与体积吗？各个图形之间的特征有什么联系？1、表面积:（1）它们的表面积是多少？（先让学生独立完成后全班交流）师：长方体和三棱柱的表面积还有其他不同的算法吗?（2）你们有什么发现？它们的表面积都可以用侧面积+两个底面积来计算（3）课件演示立体图形的平面展开图：课件展示：侧面积+两个底面积2、体积（1）它们的体积是多少？（先让学生独立完成后全班交流）（2）你有什么发现？它们的体积都可以用底面积×高来计算。

3.议一议：有一位同学说：“圆锥的体积是圆柱体积的1/3。

”你们认为他说得对吗？4、圆柱和圆锥的体积相等，高也相等，它们的底面积之间有什么关系？三、综合应用1、一个酒瓶里面深30厘米,底面直径是8厘米,瓶里有酒深10厘米,把酒瓶塞紧后倒置(瓶口向下),这时酒深20厘米。

酒瓶的容积是多少毫升?（先让学生独立完成，后全班交流）2、用一底面边长为2分米，高为5分米长方体木料做一个最大的圆柱，木料的利用率是多少？四、拓展延伸有一张长为12厘米，宽为6厘米的长方形卡纸，如果要把它折成高是6厘米的长方体或者圆柱体，它们的体积是多少立方厘米？先让学生独立思考并计算出结果，然后全班交流汇总你有什么发现？小组讨论后全班交流五、课后思考如果把它折成高是12厘米的长方体或者圆柱体，它们的体积是多少？六、总结收获这节课你有什么收获？。

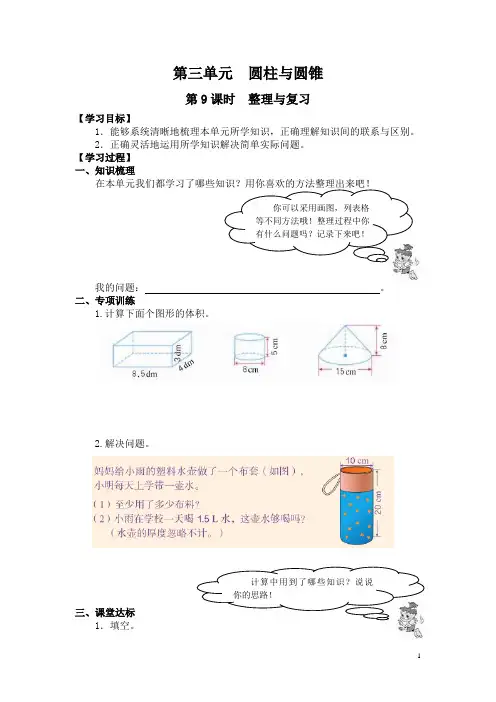
第三单元圆柱与圆锥第9课时整理与复习【学习目标】1．能够系统清晰地梳理本单元所学知识，正确理解知识间的联系与区别。

2．正确灵活地运用所学知识解决简单实际问题。

【学习过程】一、知识梳理在本单元我们都学习了哪些知识？用你喜欢的方法整理出来吧！我的问题：。

二、专项训练1.计算下面个图形的体积。

2.解决问题。

三、课堂达标1．填空。

你可以采用画图，列表格等不同方法哦！整理过程中你有什么问题吗？记录下来吧！计算中用到了哪些知识？说说你的思路！（1）一个圆柱和一个圆锥等底等高，圆锥的体积是24立方米，圆柱的体积是（），如果圆柱的体积比圆锥的体积大18立方米，圆柱的体积是（），圆锥的体积是（）。

（2）用一张长15厘米，宽12厘米的长方形纸围成一个圆柱，这个圆柱的侧面积是（）平方厘米。

（3）一个圆柱体削成一个与它等底等高的圆锥体, 削去的部分是圆锥体的( )%．2.同学们用彩纸制作了20个圆柱形灯罩，每个灯罩高35cm，底面圆的周长是47.1cm 。

至少需要用多少彩纸？想一想是要求圆柱的什么呀？3.一个圆锥形沙堆，底面积是28.26㎡，高是2.5m。

用这堆沙在10m宽的公路上铺2cm厚的路面，能铺多少米？计算时要注意单位哦！4.一块蜂窝煤大约需要用煤多少立方分米？（得数保留整数）四、课外拓展压路机的前轮是圆柱形，轮宽1.5米，直径1.2米，前轮每分钟转动10周，每分钟前进多少米？每分钟压路多少平方米？为什么要规定“先乘除后加减”？对于这个问题，我们分两层来谈。

第一层先谈谈规定运算顺序的必要性，第二层再谈谈为什么要规定“先乘除后加减”。

（1）规定运算顺序的必要性。

先举两个例子予以说明。

例1 小勇买了一块橡皮，价18分，又买了3支铅笔，每支12分，一共多少钱？综合算式18＋12×3=18＋36=54（分）=5角4分根据题意，这道题先算乘法后算加法是合情合理的。

例2 小春有18分钱，小敏有12分钱，小冬的钱数是他们俩人钱数之和的3倍，问小冬有多少钱？解答这道题的时候应该先求出小春与小敏两人钱数之和，即求出（18＋12=）30分，然后再求出30分的3倍，即（30×3=）90分。