北师大版小学数学六年级下册圆柱和圆锥

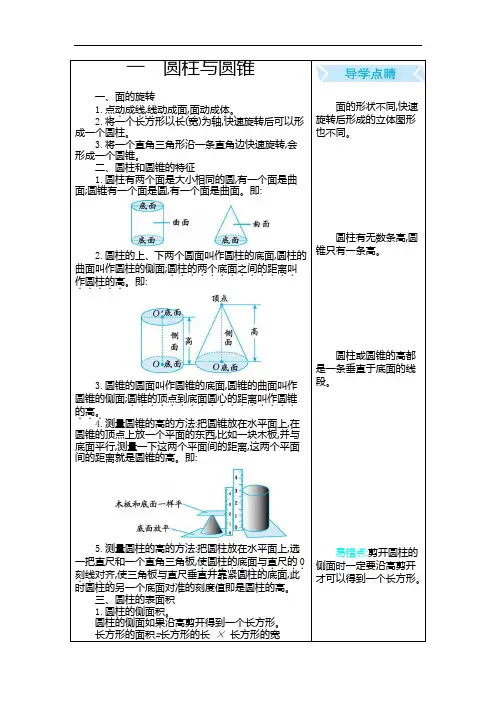
一 圆柱与圆锥一、面的旋转 1.点动成线．．．．,．线动成面．．．．,．面动成体。

．．．．．2.将一个长方形以长(宽)为轴,快速旋转后可以形成一个圆柱。

3.将一个直角三角形沿一条直角边快速旋转,会形成一个圆锥。

二、圆柱和圆锥的特征1.圆柱有两个面是大小相同的圆,有一个面是曲面;圆锥有一个面是圆,有一个面是曲面。

即:2.圆柱的上、下两个圆面叫作圆柱的底面,圆柱的曲面叫作圆柱的侧面;圆柱的两个底面之间的距离叫．．．．．．．．．．．．．作圆柱的高．．．．．。

即:3.圆锥的圆面叫作圆锥的底面,圆锥的曲面叫作圆锥的侧面;圆锥的顶点到底面圆心的距离叫作圆锥．．．．．．．．．．．．．．．．．的高。

．．．4.测量圆锥的高的方法:把圆锥放在水平面上,在圆锥的顶点上放一个平面的东西,比如一块木板,并与底面平行,测量一下这两个平面间的距离,这两个平面间的距离就是圆锥的高。

即:5.测量圆柱的高的方法:把圆柱放在水平面上,选一把直尺和一个直角三角板,使圆柱的底面与直尺的．．．．．．．．．．0．刻线对齐．．．．,使三角板与直尺垂直并靠紧圆柱的底面,此时圆柱的另一个底面对准的刻度值即是圆柱的高。

三、圆柱的表面积1.圆柱的侧面积。

圆柱的侧面如果沿高剪开得到一个长方形。

长方形的面积=长方形的长 × 长方形的宽面的形状不同,快速旋转后形成的立体图形也不同。

圆柱有无数条高,圆锥只有一条高。

圆柱或圆锥的高都是一条垂直于底面的线段。

易错点:剪开圆柱的侧面时一定要沿高剪开才可以得到一个长方形。

↓ ↓ ↓ 圆柱的侧面积=圆柱的底面周长×圆柱的高 用字母表示:S 侧=Ch 或S 侧=πdh 或S 侧=2πrh2.圆柱的表面积。

圆柱的表面积．．．．．．=．侧面积．．．+．两个底面积．．．．．不同的圆柱形实物,它们的表面积也不相同。

比如圆柱形烟囱的表面积等于烟囱的侧面积,圆柱形水桶的表面积就是水桶的侧面积加上一个底面积。

四、圆柱的体积1.意义:圆柱形物体所占空间的大小叫作圆柱的体积。

北师大版六年级（下册）数学知识要点归纳第一单元圆柱和圆锥1、“点、线、面、体”之间的关系是：点的运动形成线；线的运动形成面；面的旋转形成体。

2、圆柱的特征：（1）圆柱的两个底面是半径相等的两个圆，侧面是曲面。

（2）两个底面间的距离叫做圆柱的高。

（3）圆柱有无数条高，且高的长度都相等。

（4）圆柱是由长方形绕长或宽旋转360度得到的立方体，所以沿高线切割后的切面是长方形。

3、圆锥的特征：（1）圆锥的底面是一个圆，和底面相对的位置有一个顶点。

（2）圆锥的侧面是一个曲面。

（3）圆锥只有一条高。

（4）圆锥是由直角三角形绕一条直角边旋转360度得到的立方体，所以沿高线切割后的切面是等腰三角形。

4、沿圆柱的高剪开，圆柱的侧面展开图是一个长方形（或正方形）（如果不是沿高剪开，有可能还会是平行四边形）。

圆柱的侧面积＝底面周长×高，用字母表示为：S侧＝Ch。

圆柱的侧面积公式的应用：（1）已知底面周长和高，求侧面积，可运用公式：S侧＝ch；（2）已知底面直径和高，求侧面积，可运用公式：S侧＝πdh；（3）已知底面半径和高，求侧面积，可运用公式：S侧＝2πrh圆柱表面积的计算方法：如果用S侧表示一个圆柱的侧面积，S底表示底面积，d表示底面直径，r表示底面半径，h表示高，那么这个圆柱的表面积为：S表=S侧+2S底或S表=πdh+πd2/2或S表=2πrh+2πr2圆柱表面积的计算方法的特殊应用：（1）圆柱的表面积只包括侧面积和一个底面积的，例如无盖水桶等圆柱形物体。

（2）圆柱的表面积只包括侧面积的，例如烟囱、油管等圆柱形物体。

5、圆柱的体积：一个圆柱所占空间的大小。

6、圆柱体积公式的推导：复习六年级上册圆的面积公式的推导：把圆等分的份数越多，拼成的图形就越接近平行四边形或长方形。

拼成的平行四边形的底相当于圆周长的一半，高相当于圆的半径；拼成的长方形的长相当于圆周长的一半，宽相当于圆的半径。

所以圆的面积=π×半径×半径=π×半径2如同，圆的面积公式的推导，也可以沿着圆柱底面的扇形和圆柱的高把圆柱切开，把它分成若干等份，分得越细越好，再把它拼成一个近似长方体的立体图形，形状改变了，但体积没变，那么就可以发现拼成的这个长方体的底面积与圆柱的底面积是相等的，长方体的高也与圆柱的高相等，而长方体的体积=底面积×高，也就等于圆柱的体积。

北师大版六年级下册数学全册教案第一单元圆柱与圆锥单元教学内容：面的旋转圆柱的表面积圆柱的体积圆锥的体积单元教学目标：一、结合具体情境和操作活动，引导学生整体把握“点、线、面、体”之间的联系。

二、从多种角度探讨圆柱和圆锥的特点。

3、探讨圆柱表面积的计算方式，进展空间观念。

4、经历圆柱和圆锥体积计算方式的探讨进程，体会“类比”的思想。

五、在解决实际问题顶用活所学知识，感受数学与生活的联系。

单元教材分析：学生已经直观熟悉了长方体、正方体、圆柱和球，并初步了解了长方形、正方形、圆等平面图形的性质，学习了这些图形的面积计算，学生还熟悉了长方体（正方体），把握了长方体（正方体）表面积与体积的含义及其计算方式。

在此基础上，本单元进一步学习圆柱和圆锥的知识。

本单元要紧通过五个活动，引导学生学习面的旋转（圆柱和圆锥的熟悉）、圆柱的表面积、圆柱的体积、圆锥的体积等内容，并参与实践活动。

本单元教材编写力图表现以下要紧特点：1.结合具体情境和操作活动，引导学生经历“点动成线”“线动成面”“面动成体”的进程，体会“点、线、面、体”之间的联系教材的第一个活动表现的内容是“由平面图形通过旋转形成几何体”，这不仅是对几何体形成进程的学习，同时体会面和体的关系也是进展空间观念的重要途径，这也是教材将此课题目定为“面的旋转”的缘故。

教材呈现了几个生活中的具体情境，鼓舞学生进行观看，激活学生的生活体会，使学生经历“点动成线”“线动成面”“面动成体”的进程。

在结合具体情境感受的基础上，教材又设计了一个操作活动，通过快速旋转小旗，引导学生结合空间想象体会立体图形的形成进程，进展空间观念。

教材还提供了假设干由面旋转成体的练习。

2.重视操作与试探、想象相结合，进展学生的空间观念操作与试探、想象相结合是学生熟悉图形、探讨图形特点、进展空间观念的重要途径。

在本单元中，教材重视学生操作活动的安排，在每一个主题活动中都安排了操作活动，增进学生明白得数学知识、进展空间观念。

新北师大版小学六年级数学下册全套教案第一单元圆柱与圆锥课后反思：单元目标：通过动手操作、观察等活动，认识圆柱与圆锥。

了解圆柱与圆锥的基本特征，知道圆柱与圆锥各部分的名称。

经历由面旋转成圆柱与圆锥的活动，体会面与体之间的关系，在参与教学活动中积累活动经验，丰富对现实空间的认识，发展空间观念。

经历圆柱侧面展开等活动，认识圆柱展开图，探索并掌握圆柱表面积的计算方法。

并能运用圆柱表面积的知识解决生活中一些简单的问题。

经历“类比猜想-验证”的活动，探索并掌握圆柱和圆锥体积的计算方法，体验某些实物体积的测量方法，体会圆柱、圆锥体积知识在生活中的实际应用，解决一些简单的实际问题。

单元重点：1.能正确描述圆柱与圆锥的特征，认识圆柱和圆锥及其各部分名称。

2.能正确描述圆柱表面积的含义，能正确计算圆柱的表面积。

3.能正确计算圆柱和圆锥的体积。

4.能根据不同的问题情境正确选择相应的计算方法解决一些简单的实际问题。

单元难点：1.能正确描述圆柱与圆锥的特征，认识圆柱和圆锥及其各部分名称。

2.能正确描述圆柱表面积的含义，能正确计算圆柱的表面积。

3.能正确计算圆柱和圆锥的体积。

4.能根据不同的问题情境正确选择相应的计算方法解决一些简单的实际问题。

学情分析：本单元是在学生已经探索并掌握了长方体、正方体、圆等一些常见的平面图形的特征，已经长方体、正方体的特征，并直观认识圆柱和圆锥的基础上编排的。

此前对圆面积公式的探索以及长方体、正方体特征和表面积、体积计算方法的探索，为进一步学习本单元知识奠定了知识基础，同时也积累了探索的经验，准备了研究的方法。

圆柱和圆锥是小学阶段学习几何知识的最后一部分内容。

圆柱与圆锥是基本的几何形体，也是生产、生活中经常遇到的几何形体，这些都是本单元知识学习的重要基础。

学习圆柱和圆锥的知识扩大了学生认识形体的范围，增加了形体的知识，促进空间观念的进一步发展。

从认识长方体和正方体这样由几个平面图形围成的几何体，到认识圆柱和圆锥这样含有曲面的几何体，在图形的认识上又深入了一步。

北师大版数学六年级(下册)圆柱与圆锥经典易错题型一、圆柱与圆锥1．一个底面半径为12厘米的圆柱形杯中装有水，手里浸泡了一个底面直径是12厘米，高是18厘米的圆锥体铁块，当铁块从杯中取山来时，杯中的水面会下降多少厘米??【答案】解： ×3.14×（12÷2）2×18÷（3.14×122）= ×3.14×36×18÷（3.14×144）=1.5（厘米）答：桶内的水将下降1.5厘米。

【解析】【分析】水面下降部分水的体积就是圆锥的体积，根据圆锥的体积公式先计算出圆锥体铁块的体积，也就是水面下降部分水的体积。

用水面下降部分水的体积除以杯子的底面积即可求出水面下降的高度。

2．一个圆锥体形的沙堆，底面周长是25.12米，高1.8米，用这堆沙在8米宽的公路上铺5厘米厚的路面，能铺多少米？【答案】解：5厘米＝0.05米沙堆的底面半径：25.12÷（2×3.14）＝25.12÷6.28＝4（米）沙堆的体积： ×3.14×42×1.8＝3.14×16×0.6＝3.14×9.6＝30.144（立方米）所铺沙子的长度：30.144÷（8×0.05）＝30.144÷0.4＝75.36（米）．答：能铺75.36米。

【解析】【分析】根据1米=100厘米，先将厘米化成米，除以进率100，然后求出沙堆的底面半径，用公式：C÷2π=r，要求沙堆的体积，用公式：V=πr2h，最后用沙堆的体积÷（公路的宽×铺沙的厚度）=铺沙的长度，据此列式解答.3．一个酒瓶里面深30cm，底面内直径是10cm，瓶里酒深15cm。

把瓶口塞紧后使其瓶口向下倒立，这时酒深25cm。

求酒瓶的容积。

【答案】解：3.14×（10÷2）2×[15+(30-25)]=1570(cm3)答：酒瓶的容积是1570 cm3。

北师大版六年级数学下册知识点第一单元《圆柱与圆锥》知识点点动成线，线动成面，面动成体。

圆柱的上、下两个面叫做圆柱的底面。

它们是大小相等的两个圆。

侧面是一个曲面。

沿圆柱的高剪开，圆柱的侧面展开图是一个长方形或正方形（底面周长和高相等时，展开是一个正方形），如果斜着剪，圆柱的侧面展开图是平行四边形。

圆柱两个底面之间的距离叫做高，圆柱有无数条高。

圆锥只有一个底面，是一个圆形。

侧面是一个曲面，圆锥侧面展开是一个扇形。

圆锥的顶点到底面圆心的距离是圆锥的高，圆锥只有一条高。

把圆柱沿底面直径切开，切面是长方形或正方形。

当底面直径与高相等时是正方形。

把圆柱垂直于高切下去，切面是个圆形。

把圆锥沿高切下去，切面是个三角形。

圆柱的侧面积＝底面周长×高，字母公式是S=Ch=πdh=2πrh 。

C=S ÷h h=S ÷C圆柱的表面积=侧面积+底面积，在计算时要注意它有几个底面。

圆柱的体积＝底面积×高，字母公式是V=Sh=πr 2 h S=V ÷h h=V ÷S圆柱的体积等于和它等底等高的圆锥体积的3倍。

圆锥体积=31×底面积×高 V=31Sh S=V ×3÷h h=V ×3÷S第二单元《比例》知识点表示两个比相等的式子叫作比例。

两端的两项叫作比例的外项，中间的两项叫作比例的内项在比例里，两个内项的积等于两个外项的积。

图上距离和实际距离的比，叫作这幅图的比例尺。

比例尺是一个最简单的整数比，它没有计量单位，也不能是一个具体的数。

图上距离︰实际距离=比例尺 图上距离=实际距离×比例尺实际距离=图上距离÷比例尺比例尺的分类：按形式分，分为线段比例尺和数值比例尺。

按用途分，分为缩小比例尺和放大比例尺。

图形放大前后对应线段长的比相等。

图形缩小前后对应线段长的比相等。

放大或者缩小，只改变图形的大小，不改变图形的形状。

六年级下册数学圆柱与圆锥的重难点题型一、高的变化引起表面积的变化底面积不变，圆柱高的变化引起表面积的变化，由于底面积没有变，所以实际上发生变化的是侧面积，由此可以求出底面周长，进而求出表面积。

【例题】一个圆柱被截去10厘米后(如下图)，圆柱的表面积减少了628平方厘米，原来圆柱的表面积是多少平方厘米?(π取3.14)2、一个圆柱，如果把它的高截短3m，它的表面积就会减少94.2m²，那么这个圆柱的体积减少多少立方米?【练习】1、一个圆柱体，高减少2厘米，表面积就减少了50.24平方厘米，圆柱的底面积是多少平方厘米?2、一个圆柱的底面直径为4厘米，如果高增加1厘米，表面积增加多少平方厘米。

一个圆柱的底面周长和高相等，如果高缩短了2厘米，表面积就减少12.56平方厘米，求这个圆柱体原来的表面积?二：圆柱竖切引起的表面积变化垂直于底面切(竖切)：多出的两个面是长方形，即以底面圆的直径为长，以圆柱的高为宽的长方形。

【例题】工人把一根高是1米的圆柱形木料，沿底面直径平均分成两部分，这时两部分的表面积之和比原来增加了0.8平方米。

求这根木料原来的表面积。

【练习】1、一个底面半径4cm，高5cm的圆柱，如果沿底面直径把它平均切成两半，它的表面积增加了多少平方厘米?2、把一个半径2分米、长1米的圆木平均截成3段，表面积共增加多少平方分米?3、把一个底面半径是40cm，长是12分米的圆柱形木头锯成长短不同的4小段圆柱形木头，表面积增加了多少平方分米?4、把一根长为1.2米的圆柱形钢材截成3段，表面积增加了6.28平方分米，原来这根钢材的体积是多少?5、底面直径是20厘米的圆钢，将其截成两段同样的圆钢，两段表面积的和为7536平方厘米，原来圆钢的体积是多少立方厘米?【例题】把一个底面半径是6cm的圆柱切拼成一个近似的长方体后(如图)，表面积增加了180cm²，原来圆柱的体积是多少立方厘米?【练习】1、把一个高为1米的圆柱体切成底面是许多相等的扇形，再拼成一个近似的长方体，已知拼成后长方体表面积比原来圆柱表面积增加了40平方分米，原来圆柱体的体积是多少立方分米?2、把高5厘米的圆柱底面分成若干等份，把圆柱切开拼成一个近似的长方体，长方体表面积比圆柱增加20平方厘米。

（北师大版）六年级数学下册知识点归纳总结第一单元圆柱和圆锥1、“点、线、面、体”之间的关系是：点的运动形成线；线的运动形成面；面的旋转形成体。

2、圆柱的特征：（1）圆柱的两个底面是半径相等的两个圆，侧面是曲面。

（2）两个底面间的距离叫做圆柱的高。

（3）圆柱有无数条高，且高的长度都相等。

（4）圆柱是由长方形绕长或宽旋转360度得到的立方体，所以沿高线切割后的切面是长方形。

3、圆锥的特征：（1）圆锥的底面是一个圆，和底面相对的位置有一个顶点。

（2）圆锥的侧面是一个曲面。

（3）圆锥只有一条高。

（4）圆锥是由直角三角形绕一条直角边旋转360度得到的立方体，所以沿高线切割后的切面是等腰三角形。

4、沿圆柱的高剪开，圆柱的侧面展开图是一个长方形（或正方形）（如果不是沿高剪开，有可能还会是平行四边形）。

圆柱的侧面积=底面周长×高用字母表示为：S侧＝Ch。

圆柱的侧面积公式的应用：（1）已知底面周长和高，求侧面积，可运用公式：S侧＝ch；（2）已知底面直径和高，求侧面积，可运用公式：S侧＝πdh；（3）已知底面半径和高，求侧面积，可运用公式：S侧＝2πrh。

圆柱表面积的计算方法：如果用S侧表示一个圆柱的侧面积，S底表示底面积，d表示底面直径，r表示底面半径，h表示高，那么这个圆柱的表面积为：S表=S侧+2S底或S表=πdh+πd2/2 或S表=2πrh+2πr2圆柱表面积的计算方法的特殊应用：（1）圆柱的表面积只包括侧面积和一个底面积的，例如无盖水桶等圆柱形物体。

（2）圆柱的表面积只包括侧面积的，例如烟囱、油管等圆柱形物体。

5、圆柱的体积：一个圆柱所占空间的大小。

6、圆柱体积公式的推导：复习六年级上册圆的面积公式的推导：把圆等分的份数越多，拼成的图形就越接近平行四边形或长方形。

拼成的平行四边形的底相当于圆周长的一半，高相当于圆的半径；拼成的长方形的长相当于圆周长的一半，宽相当于圆的半径。

所以：圆的面积=π×半径×半径=π×半径²。

《圆柱与圆锥》单元整体设计一、单元主题解读（一）课程标准要求分析新课标关于本单元的要求，主要表现在“内容要求”“学业要求”“教学提示”三个方面。

内容要求:认识圆柱，了解圆柱的展开图，探索并掌握圆柱的体积和表面积的计算公式，认识圆锥，并探索其体积的计算公式，能用这些公式解决简单的实际问题。

在图形认识与测量的过程中，进一步形成量感、空间观念和几何直观。

学业要求：认识圆柱，能说出圆柱的特征，能辨认圆柱展开图，会计算圆柱体积和表面积；认识圆锥，能说出圆锥的特征，会计算圆锥的体积；能用相应公式解决简单的实际问题，形成空间观念和初步的应用意识。

教学提示:借助现实生活中的实物，引导学生通过观察、操作等活动，认识圆柱和圆锥等立体图形的特征，沟通立体图形之间的联系，如圆柱和圆锥的相同点和不同点，以及平图形和立体图形之间的关系，增添空间想象力。

引导学生经历体积单位的确定过程，通过操作、转化等活动，探索立体图形的体积和表面积的计算方法，让学生借助折叠纸盒等活动经验，认识立体图形有展开图，建立立体图形与展开后的平面图形之间的联系，培养空间观念和空间想象能力。

本单元培养学生核心素养主要表现为:分析能力、概括能力、抽象能力、推理能力、转化意识。

（二）单元教材内容分析本单元内容涉及圆柱和圆锥的形成及特点，圆柱的表面积、圆柱和圆锥的体积等知识，是图形与几何的知识。

主要培养学生的空间观念和转化思想。

本单元主要目的让学生认识圆柱和圆锥的特征，掌握圆柱的表面积和体积、圆锥的体积的计算方法，并能用它们的计算方法解决一些实际问题。

在探究知识的过程中，培养空间观念和空间想象能力。

教材在编排上多从学生的实际出发，通过动手操作、实验等方式获取知识，重点培养了学生动手操作能力。

单元学习前后内容联系：学习本单元内容之前，学生已经认识了圆柱的，掌握了长方体、正方体的特征，及表面积和体积的计算方法。

这为本单元的学习奠定了基础。

对于六年级学生，已经形成了一定空间观念和空间想象能力，但逻辑思维能力和动手操作能力有待提高。

圆柱与圆锥知识点归纳12?圆锥体的体积公式：rhs?一、32?rhs?二、圆柱体的体积公式：三、面积、体积单位的换算：1平方米=100平方分米=10000平方厘米610 =立方厘米=1000立方分米=1000000立方厘米1立方米=1立方厘米=1000立方厘米，1毫升=10001立方分米=1升毫升练习一、填空题）立方厘分米，体积是（、一个圆锥体的底面半径是6厘米，高是11 米。

）立方厘米，这个圆锥的高是（ 3厘米，体积是6.282、圆锥的底面半径是厘米。

，( )这个( )的长等于圆柱底面的3、把圆柱的侧面沿高剪开，得到一个( )，。

( )，所以圆柱的侧面积等于( )宽等于圆柱的立方分米立方米＝( )415平方厘米＝( )平方分米 4.54、）立方米 4070立方分米=（( ) 2.4立方分米＝( )升毫升）立方厘米立方分米40立方厘米＝（3 ）毫升）升（ 325 立方米＝（）立方分米， 538 升＝（平方分米的圆12分米正方体容器装满水后，倒入一个底面积是5、一个棱长是4 ）分米。

锥体容器里正好装满，这个圆锥体的高是（平方厘米，原钢20206、一根长厘米的圆钢，分成一样长的两段，表面积增加立方厘米。

材的体积是( ) ）面积是,厘米的圆柱侧面展开后得到一个（ 107、底面直径和高都是）立方厘米。

平方厘米，体积是（ ( )18、等底等高的圆柱体和圆锥体的体积比是（ )二、判断：1. 圆柱体的体积与圆锥体的体积比是3 ∶1。

（）2. 圆柱体的高扩大2倍，体积就扩大2倍。

（）3. 等底等高的圆柱和圆锥，圆柱的体积比圆锥的体积大2倍。

( )4. 圆柱体的侧面积等于底面积乘以高。

（）5. 圆柱体的底面直径是3厘米，高是9.42厘米，它的侧面展开后是一个正方形。

（）三、选择：（填序号）1. 圆柱体的底面半径扩大3倍,高不变,体积扩大（）。

A、3倍B、9倍C、6倍2.把一个棱长4分米的正方体木块削成一个最大的圆柱体，体积是（）立方分米。

北师大版数学六年级(下册)圆柱与圆锥经典易错题型一、圆柱与圆锥1.看图计算.(1)求圆柱的表面积(单位：dm)(2)求零件的体积(单位：cm)【答案】(1)解：3.14x10x20+3.14x (10“)2x2= 628+3.14x25x2= 628+157= 785 (平方分米)答：圆柱的表面积是785平方分米。

(2)解：x3.14x (2“)2x3+3.14x (2“)2x4=x3.14x1x3+3.14x1x4=3.14+12.56= 15.7 (立方厘米)答：零件的体积是15.7立方厘米。

【解析】【分析】(1)圆柱的表面积是两个底面积加上一个侧面积，根据圆面积公式计算出底面积，用底面周长乘高求出侧面积；1(2)圆柱的体积=底面积x高，圆锥的体积=底面积x高x ,根据公式计算，用圆柱的体积加上圆锥的体积就是总体积。

2.如图，一个内直径是20cm的纯净水水桶里装有纯净水，水的高度是22cm.将水桶倒放时，空余部分的高度是3cm,无水部分是圆柱形.这个纯净水水桶的容积是多少升?【答案】解：3.14x (20+2) 2x22+3.14x (20+2) 2x3=3.14x100x(22+3) =3.14x100x25=7850(立方厘米)7850立方厘米=7.85升答：这个纯净水水桶的容积是7.85升。

【解析】【分析】水桶的容积包括水的体积和空余部分的体积，根据圆柱的体积公式分别计算后再相加即可求出水桶的容积。

3.有一个底面直径为20厘米的装有一些水的圆柱形玻璃杯，已知杯中水面距杯口2.24厘米.若将一个半径为9厘米的圆锥形铅锤完全浸入水中，水会溢出314立方厘米.求铅锤的高.【答案】解：3.14x (20“)2x2.24+314= 3.14x100x2.24+314= 703.36+314= 1017.36 (立方厘米)，1017.36 + (3.14x92)= 1017.36x3+254.34= 3052.08+254.34=12 (厘米)，答：铅锤的高是12厘米。