吉林大学大学物理作业答案综合练习题(下)(二)页PPT文档

物理化学问答题第一定律部分1、 1、为什么第一定律数学表示式dU=δQ-δW 中内能前面用微分号d ， 而热量和功的前面用δ符号？答：因为内能是状态函数，具有全微分性质。

而热量和功不是状态函数，其微小改变值用δ表示。

2、 2、公式H=U+PV 中H > U,发生一状态变化后有ΔH =ΔU +Δ（PV ），此时ΔH >ΔU 吗？为什么？答：不一定。

因为Δ（PV ）可以为零、正数和负数。

3、 3、ΔH = Qp , ΔU = Qv 两式的适用条件是什么？答：ΔH = Qp 此式适用条件是：封闭系等压非体积功为零的体系。

ΔU = Qv 此式适用条件是：封闭系等容非体积功为零的体系。

4、 4、ΔU=dTCT Tv⎰21，ΔH=dTCp T T⎰21两式的适用条件是什么？答：ΔU=dTCT Tv⎰21此式适用条件是：封闭系等容非体积功为零的简单状态变化体系。

ΔH=dTCp T T ⎰21此式适用条件是：封闭系等压非体积功为零的简单状态变化体系。

5、 5、判断下列说法是否正确（1）状态确定后，状态函数的值即被确定。

答：对。

（2）状态改变后，状态函数值一定要改变。

答：不对。

如：理想气体等温膨胀过程，U 和H 的值就不变化。

（3）有一个状态函数值发生了变化，状态一定要发生变化。

答：对。

6、 6、理想气体绝热向真空膨胀，ΔU=0，ΔH=0对吗？答：对。

因理想气体绝热向真空膨胀过程是一等温过程。

7、恒压、无相变的单组分封闭体系的焓值当温度升高时是增加、减少还是不变？ 答：增加。

7、 7、在P Ø下，C （石墨）+O 2（g ）——>CO 2（g ）的反应热为Δr H θm ，对于下列几种说法，哪种不正确？（A ）Δr H θm 是CO 2的标准生成热，（B ）Δr H θm 是石墨的燃烧热，（C ）Δr H θm=Δr U m ，（D ）Δr H θm >Δr U m 答：D 不正确。

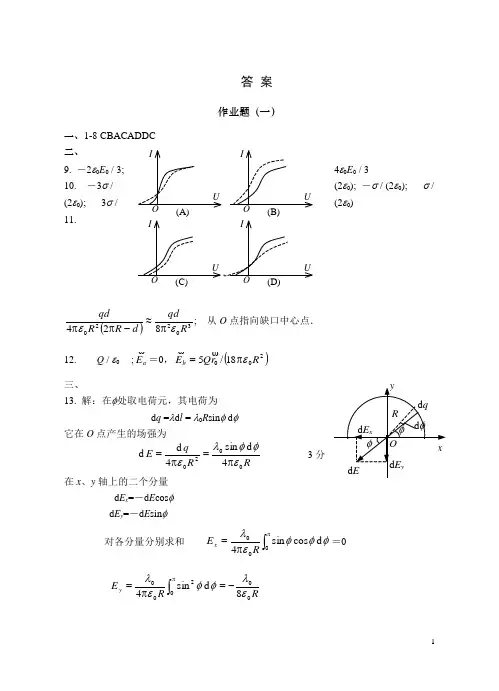
答案作业题 (一）一、1-8 CBACADDC 二、4ε0E 0 / 39. －2ε0E 0 / 3; 10. －3σ / (2ε0); －σ / (2ε0); σ / (2ε0); 3σ / (2ε0)11.()30220824Rqdd R R qd εεπ≈-ππ; 从O 点指向缺口中心点． 12. Q / ε0 ;a E ＝0，()20018/5R r Q E b επ=三、13. 解：在φ处取电荷元，其电荷为d q =λd l = λ0R sin φ d φ它在O 点产生的场强为R R qE 00204d sin 4d d εφφλεπ=π= 3分 在x 、y 轴上的二个分量 d E x =－d E cos φ d E y =－d E sin φ 对各分量分别求和 ⎰ππ=00d c o s s i n 4φφφελR E x ＝0RR E y 0002008d sin 4ελφφελ-=π=⎰π∴ j Rj E i E E y x008ελ-=+=14. 解:设坐标系如图所示．将半圆柱面划分成许多窄条．d l 宽的窄条的电荷线密度为θλλλd d d π=π=l R取θ位置处的一条，它在轴线上一点产生的场强为 θελελd 22d d 020RR E π=π=如图所示. 它在x 、y 轴上的二个分量为：d E x =d E sin θ , d E y =－d E cos θ对各分量分别积分 RR E x 02002d sin 2ελθθελππ=π=⎰ 0d cos 2002=π-=⎰πθθελRE y 场强 i Rj E i E E y x02ελπ=+=15. 解：在球内取半径为r 、厚为d r 的薄球壳，该壳内所包含的电荷为r r Ar V q d 4d d 2π⋅==ρ 在半径为r 的球面内包含的总电荷为403d 4Ar r Ar dV q rVπ=π==⎰⎰ρ (r ≤R)以该球面为高斯面，按高斯定理有 0421/4εAr r E π=π⋅ 得到()0214/εAr E =， (r ≤R )方向沿径向，A >0时向外, A <0时向里． 在球体外作一半径为r 的同心高斯球面，按高斯定理有 0422/4εAR r E π=π⋅ 得到 ()20424/r AR E ε=， (r >R )方向沿径向，A >0时向外，A <0时向里． 16. 解：设闭合面内包含净电荷为Q ．因场强只有x 分量不为零，故只是二个垂直于x 轴的平面上电场强度通量不为零．由高斯定理得：-E 1S 1+ E 2S 2=Q / ε0 ( S 1 = S 2 =S ) 3分则 Q = ε0S (E 2- E 1) = ε0Sb (x 2- x 1)= ε0ba 2(2a －a ) =ε0ba 3 = 8.85³10-12 C作业题（二）一、1-8 DBCDDACB 二、9. 10cm 10.⎪⎭⎫⎝⎛π∆-π20414R S R Q ε 11. Q / (4πε0R 2); 0 ; Q / (4πε0R ); Q / (4πε0r 2)12. 0d =⋅⎰Ll E单位正电荷在静电场中沿任意闭合路径绕行一周，电场力作功等于零 有势（或保守力）三、13. 解：将题中的电荷分布看作为面密度为σ的大平面和面密度为－σ的圆盘叠加的结果．选x 轴垂直于平面，坐标原点Ｏ在圆盘中心，大平面在x 处产生的场强为i x x E012εσ=圆盘在该处的场强为i x R x x E ⎪⎪⎭⎫ ⎝⎛+--=2202112εσ ∴ i x R xE E E 220212+=+=εσ该点电势为 ()22002202d 2x R R x R x x U x +-=+=⎰εσεσ14. 解: 由高斯定理可知空腔内E ＝0，故带电球层的空腔是等势区，各点电势均为U .在球层内取半径为r →r ＋d r 的薄球层．其电荷为d q = ρ 4πr 2d r该薄层电荷在球心处产生的电势为 ()00/d 4/d d ερεr r r q U =π= 整个带电球层在球心处产生的电势为 ()21220002d d 21R R r r U U R R -===⎰⎰ερερ 因为空腔内为等势区所以空腔内任一点的电势U 为 ()2122002R R U U -==ερ若根据电势定义⎰⋅=l E Ud 计算同样给分.15.解：设内球上所带电荷为Q ，则两球间的电场强度的大小为204r QE επ= (R 1＜r ＜R 2)两球的电势差⎰⎰π==212120124d R R R R r drQ r E U ε⎪⎪⎭⎫ ⎝⎛-π=210114R R Q ε ∴ 12122104R R U R R Q -π=ε＝2.14³10-9 C16. 解：设原点O 在左边导线的轴线上，x 轴通过两导线轴线并与之垂直．在两轴线组成的平面上，在R ＜x ＜(d －R )区域内，离原点距离x 处的P 点场强为()x d x E E E -π+π=+=-+0022ελελ 则两导线间的电势差 ⎰-=R d Rx E U d ⎰-⎪⎭⎫ ⎝⎛-+π=Rd Rx x d x d 1120ελ()[]R d Rx d x ---π=ln ln 20ελ⎪⎭⎫ ⎝⎛---π=R d R R R d ln ln 20ελ RRd -π=ln0ελ +λ作业题（三）一、1-8 CBBBDBCB 二、9. λ/(2πr )；λ/(2π ε0 εr r ) 10. ,1,r r εε11.1r ε;1rε12. 无极分子;电偶极子 三、13. 解：(1) 由静电感应，金属球壳的内表面上有感生电荷-q ，外表面上带电荷q +Q ．(2) 不论球壳内表面上的感生电荷是如何分布的，因为任一电荷元离O 点的距离都是a ，所以由这些电荷在O 点产生的电势为a dq U q 04επ=⎰-a q 04επ-=(3) 球心O 点处的总电势为分布在球壳内外表面上的电荷和点电荷q 在O 点产生的电势的代数和 q Q q q O U U U U +-++= r q 04επ=a q 04επ-b q Q 04επ++ )111(40b a r q +-π=εbQ04επ+14. 解：设导体球带电q ，取无穷远处为电势零点，则导体球电势：r qU 004επ=内球壳电势： 10114R q Q U επ-=2024R Q επ+二者等电势，即 r q04επ1014R q Q επ-=2024R Q επ+解得 )()(122112r R R Q R Q R r q ++=15. 解：(1) 令无限远处电势为零，则带电荷为q 的导体球，其电势为R qU 04επ=将d q 从无限远处搬到球上过程中，外力作的功等于该电荷元在球上所具有的电势能 q RqW A d 4d d 0επ== (2) 带电球体的电荷从零增加到Q 的过程中，外力作功为⎰⎰==QR q q A A 004d d πεR Q 028επ=16. 解：设内外圆筒沿轴向单位长度上分别带有电荷+λ和-λ, 根据高斯定理可求得两圆筒间任一点的电场强度为 rE r εελ02π=则两圆筒的电势差为 1200ln 22d d 2121R R r r r E U r R R r R R εελεελπ=π==⎰⎰⋅ 解得 120ln 2R R Ur εελπ=于是可求得Ａ点的电场强度为 A E )/l n (12R R R U== 998 V/m 方向沿径向向外A 点与外筒间的电势差： ⎰⎰=='22d )/ln(d 12RR R Rr rR R U r E U RR R R U212ln )/ln(= = 12.5 V作业题（四）一、1-8 C C D C B D B A 二、9. 1:1 10. 0; 0I μ- 11. 0I μ 12.Rihπ20μ 13. 解：(1) 圆柱形载流导体在空间的磁感强度的分布为⎪⎪⎩⎪⎪⎨⎧>π≤≤π=R r r I R r r RIB 202020μμ∴穿过ABCD 的Φ为 ⎰=R r Bl 0d Φ⎰+RRr Bl 2d 2ln 2400π+π=lI l I μμ(2) 圆筒载流导体在空间的磁感强度分布为R r R R r rIR R R r r I R r B ≤≤⎪⎪⎪⎩⎪⎪⎪⎨⎧>π--π<≈002020200220μμ 穿过 A 'B 'C 'D ' 的Φ为：⎥⎥⎦⎤⎢⎢⎣⎡+--π=⎰⎰R R RR r r r R R R r r l I 022022020d d 12μΦ=⎥⎦⎤⎢⎣⎡+--π2ln ln 2120202200R RR R R l I μ (3) 在题给条件下，筒壁中 0<B<μ0I /(2πR )，B 为有限值，当壁厚趋于零时壁截面上磁通量趋于零，即21ln 02220→-R R R R R ，可得 2ln 20π=lI μΦ14. 解：将导线分成1、2、3、4四部份，各部分在O 点产生的磁感强度设为B 1、B 2、B 3、B 4．根据叠加原理O 点的磁感强度为：4321B B B B B+++=∵ 1B 、4B 均为0，故 32B B B += 2分)2(4102RIB μ= 方向 ⊗ 2分2242)sin (sin 401203RIa IB π=-π=μββμ)2/(0R I π=μ 方向 ⊗其中 2/R a =， 2/2)4/sin(sin 2=π=β2/2)4/sin(sin 1-=π-=β∴ R I R I B π+=2800μμ)141(20π+=R I μ 方向 ⊗15. 解：由毕奥－萨伐尔定律可得，设半径为R 1的载流半圆弧在O 点产生的磁感强度为B 1，则 1014R IB μ=同理, 2024R IB μ=∵ 21R R > ∴ 21B B < 故磁感强度 12B B B -=204R I μ=104R I μ-206R Iμ=∴ 213R R = 16. 解：如图所示，圆筒旋转时相当于圆筒上具有同向的面电流密度i ，σωσωR R i =ππ=)2/(2 3分作矩形有向闭合环路如图中所示．从电流分布的对称性分析可知，在ab 上各点B 的大小和方向均相同，而且B的方向平行于ab ，在bc和fa 上各点B 的方向与线元垂直，在de , cd fe ,上各点0=B．应用安培环路定理∑⎰⋅=I l B 0d μ可得 ab i ab B 0μ=σωμμR i B 00== 圆筒内部为均匀磁场，磁感强度的大小为σωμR B 0=，方向平行于轴线朝右．作业题(五)一、1-8 ABAACBDB二、 9. 3R B πλω 10. aIB11.12. a l I 4/d 20μ三、13. 解：电子进入磁场作圆周运动，圆心在底边上．当电子轨迹 与上面边界相切时，对应最大速度，此时有如图所示情形． R R l =︒+45sin )(∴ l l R )12()12/(+=-=由 )/(eB m R v =，求出v 最大值为 mleBm eBR )12(+==v14. 解：考虑半圆形载流导线CD 所受的安培力 R IB F m 2⋅= 列出力的平衡方程式 T R IB 22=⋅ 故： IBR T = 15. 解：(1) S = ab =5³10-3 m 2p m = SI =1³10-2 (A ²m 2)，︒=60sin B p M m =4.33³10-2 N ²mβJ M =，β/M J ==2.16³10-3 kg ²m 2(2) 令从B 到m p的夹角为θ，∵ M 与角位移d θ 的正方向相反=-=⎰︒︒060d θM A ⎰︒︒-060d sin θθB p m=2.5³10-3J 16. 解：由安培环路定理：∑⎰⋅=i I l Hd0< r <R 1区域： 212/2R Ir rH =π212R Ir H π=， 2102R IrB π=μR 1< r <R 2区域： I rH =π2r I H π=2， rIB π=2μR 2< r <R 3区域： )()(22223222R R R r I I rH ---=π )1(22223222R R R r r IH ---π= )1(2222322200R R R r r IH B ---π==μμ r >R 3区域： H = 0，B = 0. O O ′ RR l45°C D作业题(六)一、1-8 D A B A B D D A 二、9. v BL sin θ ； a10. 225R B ω ; O 点11. dda b +πln 20μ12. 减小三、13. 解：大小： =⎪d Φ /d t ⎪= S d B / d t= S d B / d t =t B Oa R d /d )sin 2121(22θθ⋅-=3.68 mV方向：沿adcb 绕向．14. 解：(1) 设线圈转至任意位置时圆线圈的法向与磁场之间的夹角为θ，则通过该圆线圈平面的磁通量为θΦcos 2r B π=, nt t π==2ωθ∴ nt r B ππ=2cos 2Φ 在任意时刻线圈中的感应电动势为nt n r NB tNπππ=Φ-=2sin 2d d 2☜nt n BNr ππ=2sin 222 t ΤI nt R n NBr R i m π=ππ==22sin 2sin 22☜ 当线圈转过π /2时，t =T /4，则 987.0/22=π==2R NBn r I i m A(2) 由圆线圈中电流I m 在圆心处激发的磁场为==')2/(0r NI B m μ 6.20³10-4 T 方向在图面内向下，故此时圆心处的实际磁感强度的大小 500.0)(2/1220≈'+=B B B T方向与磁场B的方向基本相同．15. 解：由题意，大线圈中的电流Ｉ在小线圈回路处产生的磁场可视为均匀的．2/322202/32220)(2)(24x R IR x R IR B +=+ππ=μμ 故穿过小回路的磁通量为c22/32220)(2r x R IR S B π+==⋅μΦ 32202x RI r π≈μ 由于小线圈的运动，小线圈中的感应电动势为t x x IR r t i d d 23d d 4220π=Φ=μ☜v 422023x IR r π=μ 当x =NR 时，小线圈回路中的感应电动势为)2/(32420R N I r i v π=μ☜16. 解：动生电动势 ⎰⋅⨯=MNv l B MeN d )(☜为计算简单，可引入一条辅助线MN ，构成闭合回路MeNM , 闭合回路总电动势0=+=NM MeN ☜☜☜总 MN NM MeN ☜☜☜=-= 2分 x x I l B b a ba MN d 2d )(0⎰⎰⋅+-π-=⨯=μv v MN☜b a b a I -+π-=ln20v μ 负号表示MN ☜的方向与x 轴相反．ba ba I MeN -+π-=ln 20v μ☜ 方向N →Mba ba I U U MN N M -+π=-=-ln 20v μ☜作业题 (七)一、1-8 ACDCACCA 二、9. 2π (n -1) e / λ ； 4³103 10. (1) 使两缝间距变小． (2) 使屏与双缝之间的距离变大11. 2 ( n – 1) e – λ /2 或者2 ( n – 1) e + λ /212. 539.1 三、13. 解：已知：d ＝0.2 mm ，D ＝1 m ，l ＝20 mm依公式： λk l D dS ==∴ Ddlk =λ＝4³10-3 mm ＝4000 nm故当 k ＝10 λ1＝ 400 nm k ＝9 λ2＝444.4 nmk ＝8 λ3＝ 500 nm k ＝7 λ4＝571.4 nm k ＝6 λ5＝666.7 nm这五种波长的光在所给观察点最大限度地加强．14. 解：(1) ∆x ＝20 D λ / a ＝0.11 m (2) 覆盖云玻璃后，零级明纹应满足(n －1)e ＋r 1＝r 2设不盖玻璃片时，此点为第k 级明纹，则应有r 2－r 1＝k λ 所以 (n －1)e = k λ k ＝(n －1) e / λ＝6.96≈7 零级明纹移到原第7级明纹处15. 解：第四条明条纹满足以下两式：λλθ42124=+x ，即()θλ4/74=x2λλθ42124=+''x ，即()θλ'='4/74x 第4级明条纹的位移值为∆x =()()θθθθλ''-=-'4/744x x(也可以直接用条纹间距的公式算，考虑到第四明纹离棱边的距离等于3.5 个明纹间距．)16. 解：根据暗环半径公式有 R k r k λ=()R k r k λ1010+=+由以上两式可得 ()()λ10/2210k k r r R -=+ ＝4 m作业题(八) 答案一、1-8 B C B C C B D B 二、9. 1.2; 3.6 10. 4 第一暗 11. 一；三12. 6250Å (或625 nm)13. 解：(1) 由单缝衍射暗纹公式得111sin λθ=a 222sin λθ=a 由题意可知 21θθ= , 21sin sin θθ=代入上式可得 212λλ= (2) 211112sin λλθk k a == (k 1 = 1, 2, ……) a k /2sin 211λθ=222sin λθk a = (k 2 = 1, 2, ……) a k /sin 222λθ=若k 2 = 2k 1，则θ1 = θ2，即λ1的任一k 1级极小都有λ2的2k 1级极小与之重合． 14. 解：(1) 由单缝衍射明纹公式可知()111231221sin λλϕ=+=k a (取k ＝1 )()222231221sin λλϕ=+=k af x /tg 11=ϕ , f x /tg 22=ϕ 由于 11tg sin ϕϕ≈ , 22tg sin ϕϕ≈所以 a f x /2311λ=a f x /2322λ=则两个第一级明纹之间距为a f x x x /2312λ∆=-=∆=0.27 cm(2) 由光栅衍射主极大的公式 1111sin λλϕ==k d2221sin λλϕ==k d且有 f x /tg sin =≈ϕϕ所以d f x x x /12λ∆=-=∆=1.8 cm15. 解：(1) 由光栅衍射主极大公式得a +b =ϕλsin k =2.4³10-4 cm(2) 若第三级不缺级，则由光栅公式得()λϕ3sin ='+b a 由于第三级缺级，则对应于最小可能的a ，ϕ'方向应是单缝衍射第一级暗纹：两式比较，得 λϕ='sin aa = (a +b )/3=0.8³10-4 cm (3) ()λϕk b a =+sin ，(主极大)λϕk a '=sin ，(单缝衍射极小) (k ＇=1，2，3，......)因此 k =3，6，9，........缺级． 又因为k max =(a ＋b ) / λ=4, 所以实际呈现k=0，±1，±2级明纹．(k=±4在π / 2处看不到．)16. 解：由光栅衍射主极大公式得 111sin λϕk d = 222sin λϕk d =212122112132660440sin sin k k k k k k =⨯⨯==λλϕϕ 4分当两谱线重合时有 ϕ1= ϕ2即 69462321===k k ．．．．．．．两谱线第二次重合即是4621=k k ， k 1=6， k 2=4由光栅公式可知d sin60°=6λ160sin 61λ=d =3.05³10-3mm作业题 九一、选择题 1-8 ABBECBDC 二、填空题 9． 2；1/4 10． 2I 11．312． 完全（线）偏振光； 垂直于入射面； 部分偏振光 三、计算题13．解：设第二个偏振片与第一个偏振片的偏振化方向间的夹角为θ．透过第一个偏振片后的光强 I 1＝I 0 / 2． 透过第二个偏振片后的光强为I 2，由马吕斯定律，I 2＝(I 0 /2)cos 2θ 透过第三个偏振片的光强为I 3，I 3 ＝I 2 cos 2(90°－θ ) = (I 0 / 2) cos 2θ sin 2θ = (I 0 / 8)sin 22θ 由题意知 I 3＝I 2 / 16 所以 sin 22θ = 1 / 2， ()2/2sin 211-=θ＝22.5°14．解：(1) 透过第一个偏振片的光强I 1I 1＝I 0 cos 230° ＝3 I 0 / 4 透过第二个偏振片后的光强I 2， I 2＝I 1cos 260°＝3I 0 / 16 (2) 原入射光束换为自然光，则I 1＝I 0 / 2I 2＝I 1cos 260°＝I 0 / 8 15．解：由布儒斯特定律tg i 0＝1.33 得 i 0＝53.1° 16．解：(1) 设该液体的折射率为n ，由布儒斯特定律tg i 0＝1.56 / n 得 n ＝1.56 / tg48.09°＝1.40 (2) 折射角r ＝0.5π－48.09°＝41.91° (＝41°55' )作业题(十)一、1-8 D D A C C C B C 二、9. λ/hc ; λ/h ; )/(λc h10. 3.82³103 11. 5³1014 ;212. 0.0549 三、13. 解：(1) 由 A h U e a -=ν 得 e A e h U a //-=ν e h U a /d /d =ν (恒量) 由此可知，对不同金属，曲线的斜率相同．(2) h = e tg θ 1410)0.50.10(00.2⨯--=e =6.4³10-34 J ²s 14. 解：(1) )11(2n Rhc E -=∆75.12)11(6.132=-=n eVn =4 2分(2) 可以发出λ41、λ31、λ21、λ43、λ42、λ32六条谱线． 能级图如图所示．15. 解：(1) ==λν/hc h 2.86 eV ． (2) 由于此谱线是巴耳末线系，其 k =24.32/21-==E E K eV (E 1 =－13.6 eV) νh E n E E K n +==21/ 51=+=νh E E n K ． (3) 可发射四个线系，共有10条谱线． 见图 波长最短的是由n =5跃迁到n =1的谱线．λ43 λ42 λ41λ32λ31 λ21 n =4321=5=4 =3=2=1。