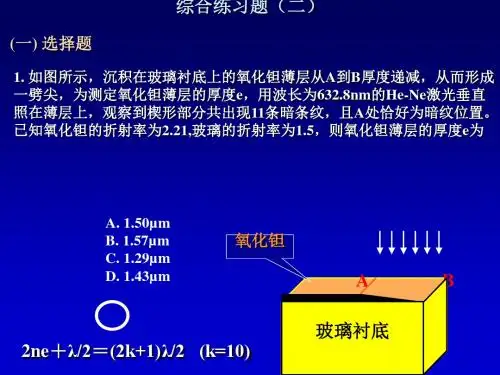
电磁波作业 吉林大学大物答案
- 格式:ppt
- 大小:718.00 KB
- 文档页数:8





3. 两根无限长平行直导线载有大小相等方向相反电流I, I以dI/dt的变化率增长,一矩形线圈位于导线平面内(如图,则A.线圈中无感应电流;B B.线圈中感应电流为顺时针方向;C C.线圈中感应电流为逆时针方向;D D.线圈中感应电流方向不确定。
4. 在通有电流I 无限长直导线所在平面内,有一半经r、电阻R 导线环,环中心距导线a,且a >> r。
当导线电流切断后,导线环流过电量为5.对位移电流,有下述四种说法,请指出哪一种说法是正确的A A.位移电流是由变化电场产生的B B.位移电流是由变化磁场产生的C C.位移电流的热效应服从焦耳-楞次定律D D.位移电流的磁效应不服从安培环路定理6.在感应电场中电磁感应定律可写成式中E K为感应电场的电场强度,此式表明A. 闭合曲线C 上E K处处相等B. 感应电场是保守力场C.感应电场的电场线不是闭合曲线D.感应电场不能像静电场那样引入电势概念1. 长直导线通有电流I ,与长直导线共面、垂直于导线细金属棒AB ,以速度V 平行于导线作匀速运动,问(1金属棒两端电势U A 和U B 哪个较高?(2若电流I 反向,U A 和U B 哪个较高?(3金属棒与导线平行,结果又如何?二、填空题U A =U BU A U B;三、计算题1.如图,匀强磁场B 与矩形导线回路法线 n 成60°角B = B = B = ktkt (k 为大于零的常数。
长为L的导体杆AB以匀速 u 向右平动,求回路中 t 时刻感应电动势大小和方向(设t = 0 时,x = 0。
解:S B mρρ⋅=φLvt kt ⋅=21dt d m i φε=221kLvt =kLvt =方向a →b ,顺时针。
ο60cos SB =用法拉第电磁感应定律计算电动势,不必再求动生电动势2. 在等边三角形平面回路ADCA 中存在磁感应强度为B 均匀磁场,方向垂直于回路平面,回路CD 段为滑动导线,它以匀速 v 远离A 端运动,并始终保持回路是等边三角形,设滑动导线CD 到A 端的垂直距离为x ,且时间t = 0 时,x = 0, 试求,在下述两种不同的磁场情况下,回路中的感应电动势和时间t 的关系。
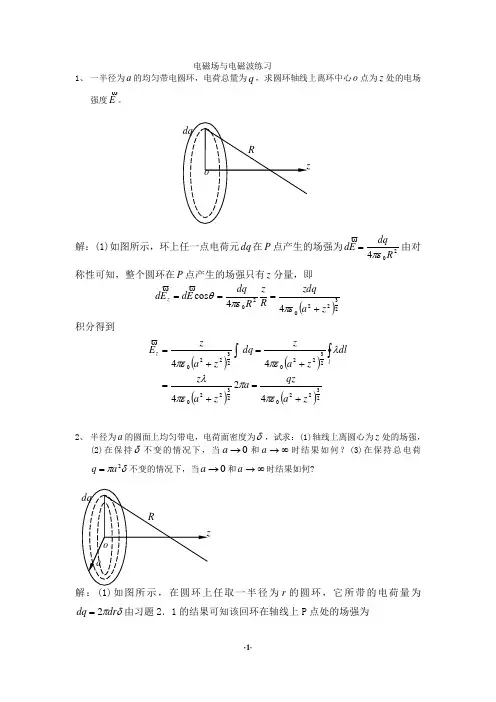
电磁场与电磁波练习1、 一半径为a 的均匀带电圆环,电荷总量为q ,求圆环轴线上离环中心o 点为z 处的电场强度E 。
解:(1)如图所示,环上任一点电荷元dq 在P 点产生的场强为204RdqE d πε=由对称性可知,整个圆环在P 点产生的场强只有z 分量,即()232202044cos z a zdq Rz R dq E d E d z +===πεπεθ 积分得到()()()()2322023220232202322042444za qza za z dlza z dq za z E lz +=+=+=+=⎰⎰πεππελλπεπε2、 半径为a 的圆面上均匀带电,电荷面密度为δ,试求:(1)轴线上离圆心为z 处的场强,(2)在保持δ不变的情况下,当0→a 和∞→a 时结果如何?(3)在保持总电荷δπ2a q =不变的情况下,当0→a 和∞→a 时结果如何?解:(1)如图所示,在圆环上任取一半径为r 的圆环,它所带的电荷量为δπdr dq 2=由习题2.1的结果可知该回环在轴线上P 点处的场强为()()23222322024zrrdrz zr zdq E d +=+=εδπε则整个均匀带电圆面在轴线上P 点出产生的场强为()⎪⎪⎭⎫⎝⎛+-=+=⎰220023220122z a zzr rdr z E a z εδεδ (2)若δ不变,当0→a 时,则0)11(20=-=εδz E ;当∞→a ,则002)01(2εδεδ=-=z E (3)若保持δπ2a q =不变,当0→a 时,此带电圆面可视为一点电荷。
则204z q E z πε=。
当∞→a 时,0→δ,则0=z E。
3、 有一同轴圆柱导体,其内导体半径为a ,外导体内表面的半径为b ,其间填充介电常数为ε的介质,现将同轴导体充电,使每米长带电荷λ。
试证明储存在每米长同轴导体间的静电能量为ab W ln 42πελ=。
证:在内外导体间介质中的电场为)(2b r a rE <<=πελ沿同轴线单位长度的储能为a b rdr r dVE dV D E W ln 4222221222πελππελεε=⎪⎭⎫⎝⎛==∙=⎰⎰⎰4、 在介电常数为ε的无限大约均匀介质中,有一半径为a 的带电q 的导体球,求储存在介质中的静电能量。