9矩阵桁架例题解析

第9章矩阵位移法习题解答习题9.1是非判断题（1）矩阵位移法既可计算超静定结构，又可以计算静定结构。

（）（2）矩阵位移法基本未知量的数目与位移法基本未知量的数目总是相等的。

（）（3）单元刚度矩阵都具有对称性和奇异性。

（）（4）在矩阵位移法中，整体分析的实质是建立各结点的平衡方程。

（）（5）结构刚度矩阵与单元的编号方式有关。

（）（6）原荷载与对应的等效结点荷载使结构产生相同的内力和变形。

（）【解】（1）正确。

（2）错误。

位移法中某些不独立的杆端位移不计入基本未知量。

（3）错误。

不计结点线位移的连续梁单元的单刚不具奇异性。

（4）正确。

（5）错误。

结点位移分量统一编码会影响结构刚度矩阵，但单元或结点编码则不会。

（6）错误。

二者只产生相同的结点位移。

习题9.2填空题（1）矩阵位移法分析包含三个基本环节，其一是结构的,其二是分析，其三是分析。

（2）已知某单元的定位向量为[3 5 6 7 8 9]七则单元刚度系数炫应叠加到结构刚度矩阵的元素中去。

（3）将非结点荷载转换为等效结点荷载，等效的原则是。

（4）矩阵位移法中，在求解结点位移之前，主要工作是形成矩阵和_________________ 列阵。

（5）用矩阵位移法求得某结构结点2的位移为4=[. V2 ft]T=[0.8 0.3 0.5]T,单元①的始、末端结点码为3、2,单元定位向量为尸＞=[0 0 0 3 4 5]T ,设单元与x轴之间的夹角为a =买，则2 尹＞ =O（6 ）用矩阵位移法求得平面刚架某单元在单元坐标系中的杆端力为F e =[7.5 -48 -70.9 -7.5 48 -121.09]T ,则该单元的轴力心=kN。

【解】（1）离散化，单元，整体；（2）灯8；（3）结点位移相等；（4）结构刚度，综合结点荷载；（5）[0 0 0 0.3 -0.8 0.5]。

（6）-7.5o离、空的值以及K ⑴中元素妍、愚、姒的值。

【解】各刚度系数的物理意义如习题解9.3图所示。

第二章 结构矩阵分析由于有限元方法起源于力学中的结构分析，本章的作用是通过三个典型问题说明有限元方法应用于结构分析时的一般步骤，并借此了解有限元方法的一些基本概念。

§2-1平面桁架（直接法，结构矩阵分析中常用的力法，处理静定问题，位移法，可处理静定&静不定）本节讨论的对象是图2-1所示的平面桁架。

组成桁架的各杆为等截面直杆，外载荷p 直接作用于杆的铰接点（结点）上。

为简单起见不妨设各杆的截面积均为Ａ，材料的弹性模量均为Ｅ。

我们可按下述步骤求得桁架的变形和内力。

１、结构的离散化 对结点及单元编号取组成桁架的每根杆为一个单元(该问题本身为一离散结构的力学问题)，以①, ②, ③ 加以编号；取杆的铰接点为结点，以１、２、３加以编号（总体结点序号）。

如图２－２所示，即：我们所讨论的桁架包括三个单元、三个结点。

各单元（杆）仅在结点处连接。

２、建立总体坐标系 并确定结点坐标和自由度为了描述结构的平衡需要建立一个坐标系，称为总体坐标系，以区别于以后出现的“局部坐标系”。

总体坐标系的选择原则上不受限制，但希望使用方便。

本节所选的总体坐标系示于图２－２，坐标原点与结点１重合。

以u, v 分别表示沿 x, y 方向的位移分量， p, q 分别表示力沿 x, y 轴的力分量（投影）。

在总体坐标系中各结点的坐标为：它们将作为程序的输入数据（几何参数）。

每个结点有两个自由度，对结点１、２、３分别为图２－１x 图２－２（x 1, y 1）=(0, 0 )、（x 2, y 2）=(a, a )、（x 3,若暂时不考虑支承约束条件，整个结构的结点自由度为 ３、单元分析（建立结点力与结点位移之间的关系） 取一个一般性的单元，设它的两个结点在结构中的编号为i, j （单元内部的结点序号）。

由材料力学可知，杆的轴向刚度为EA/L 。

其中Ｌ为杆的长度：（１）单元局部坐标系现选取一典型单元对其进行单元分析，对所分析的单元按如下方式建立一个坐标系： 原点：与结点i 重合, x ’轴：沿 i ,j 方向, y ’轴：与x ’轴垂直。

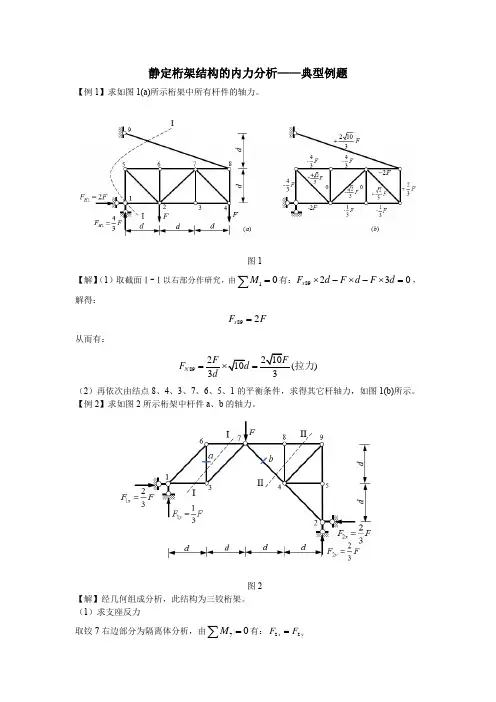
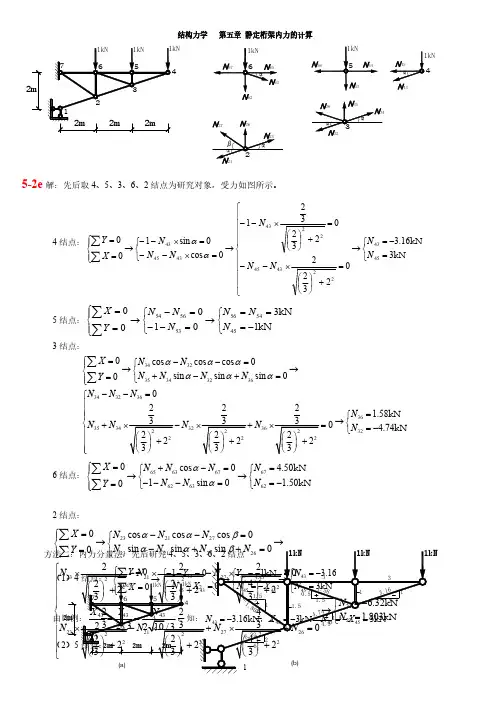
静定桁架结构的内力分析——典型例题【例1】求如图1(a)所示桁架中所有杆件的轴力。

图1【解】（1）取截面Ⅰ-Ⅰ以右部分作研究，由有：，解得：从而有：（2）再依次由结点8、4、3、7、6、5、1的平衡条件，求得其它杆轴力，如图1(b)所示。

【例2】求如图2所示桁架中杆件a 、b 的轴力。

图2【解】经几何组成分析，此结构为三铰桁架。

（1）求支座反力取铰7右边部分为隔离体分析，由有：10M =∑89230x F d F d F d ⨯-⨯-⨯=892x F F=892)3N F F d ==拉力70M =∑22x y F F =由整体平衡条件有：从而有： ， 再分别由整体平衡条件、有：， （2）作截面Ⅰ-Ⅰ，取左边作为隔离体研究，由得：（3）作截面Ⅱ-Ⅱ，取右边作为隔离体研究，由有：，解得： 从而得：。

【例3】求如图3所示桁架中杆件a 、b 的轴力。

图3【解】经几何组成分析，此结构为主从结构，截面Ⅰ-Ⅰ左边为附属部分，右边为基本部分。

杆件58、78为零杆。

（1）作截面Ⅰ-Ⅰ，取左边作为隔离体研究，由得：10M =∑2224x y F d F d F d ⨯+⨯=⨯()223x F F =←()223y F F =↑0x F =∑0y F =∑()123x F F =→()113y F F =↑0y F =∑()13Na F F =-压力80M =∑222xb x y F d F d F d ⨯+⨯=⨯23xb F F =-()Nb F =压力0y F =∑()1V F F =↑由整体平衡条件得 ，由有 （2）作截面Ⅱ-Ⅱ，取右边作为隔离体研究研究 由有：，从而得： 由有：，从而得：【例4】求如图5-7所示桁架中杆件a 、b 的轴力。

图4【解】（1）取截面Ⅰ-Ⅰ以上部分为隔离体分析，由有：，从而得：（2）取截面Ⅱ-Ⅱ以左部分为隔离体，由有：，从而得：【例5】求如图5(a)所示桁架中杆件a 、b 的轴力。

优化设计是工程设计的一种重要的科学设计方法。

本文结合优化模型及优化方法对简单的桁架优化设计问题进行了分析。

如图所示，两杆桁架结构，40cm, =30cm, F=1.2 MN s b =。

两杆的许用应力均为2[]16,000 N/cm σ=，两杆的应力应满足12[]; []σσσσ≤≤。

杆的横截面形状不限，现欲寻求该结构的最轻重量设计。

假设两杆的截面积分别为11x A =，22x A =（2cm ），欲求最轻重量即求最小总体积。

结构的总体积为2122114050A A V x x l l +=+=（3cm ） 对节点处的受力分析图如下：1.2F =2F 1= 1.6F 2=求得两杆上的受力分别为2MN F 1=， 1.6MN F 2=，由应力条件][A F 111σσ≤=，][A F 222σσ≤=，得约束条件125][11=≥σF x ，100][22=≥σF x 。

故优化模型⎪⎩⎪⎨⎧≤+-=≤+-=+=0100)(0125)(..4050),(min 22112121x x g x x g t s x x x x fsb(1)(2)F对优化模型绘出MATLAB 函数图像即可得到其设计空间，此即一线性规划问题，得到最优解为1251=x ，1002=x 时取得。

作Lagrange 函数：)100()125(4050),,,(2211212121-+-++=x x x x x x L λλλλ其KKT 条件为0)50(,0,0501111111=+=∂∂≥≤+=∂∂λλx x L x x x L 0)40(,0,0402222222=+=∂∂≥≤+=∂∂λλx x L x x x L 0)125(,0,01251111111=-=∂∂≥≥-=∂∂x x L x x L λλλ 0)100(,0,01002222222=-=∂∂≥≥-=∂∂x x L x x L λλλ 解得501-=λ，402-=λ，1251=x ，1002=x通过建模，KKT 条件分析及编程求解，得出桁架的最优设计：当（1）杆截面积1252cm ，（2）杆截面积1002cm 时的方案是最优的。

§9-6 忽略轴向变形时矩形 轴向变形 刚架的整体分析 单元定位向量 xT T0 1A 22{λ }1 = [1 {λ } = [120 2 1 0 3]3 C2 1 1 C1 1 4 03 D010 2 0 0 0]0 4 0 0 0]y{λ }3= [11 1 0 2 2 30 0B0 0T01 1 1 2 0 3 4 4 0 5 0 6 0 0 2 4 300 41 1 0 2 2 3 1 4 0 5 3 61 40 53 61 1 1 0 2 2 3 0 4 0 5 0 60 22 30 40 50 60 50 6k1k2k31 1 0 2 2 3 1 4 0 5 3 61 10 22 31 40 53 61 1 1 0 2 2 3 0 4 0 5 0 60 22 30 40 50 6 1 2 0 3 4 4 0 5 0 6 01 10 24 30 40 502 6k11 2k220 0 0 0k340 0 0 010 0 0 030 0 0 0[K]=3 4§9-7 桁架及组合结构的整体分析 一、桁架X1eX131u1e2u2X 2eY1X1 α⎡ EA ⎧ X1 ⎫ ⎢ l ⎨ ⎬ = ⎢ EA ⎩ X 2 ⎭ ⎢− ⎣ lEA ⎤ − l ⎥ ⎧u1 ⎫ EA ⎥ ⎨u2 ⎬ ⎥⎩ ⎭ l ⎦eye ⎡ ⎡ 1cos α− 1 0 ⎧ X1 ⎫ ⎢ ⎪ e ⎪ EA ⎢ ⎢ α sinα cos 0 0 Y1 = [⎪ ] ⎪ = EA ⎢ 0 2 k ⋅ ⎨ ⎬ l ⎢ − cos α l ⎢− 1 0 1 ⎪X 2 ⎪ ⎢⎢ ⎪ Y2 ⎪ ⎩ ⎭ ⎢− cosα sinα ⎣⎣ 0 0 02Y2⎧ X1 ⎫ ⎪Y ⎪ {F }e= ⎪ 1 ⎪ ⎨ ⎬ X2 ⎪X2 ⎪ xT e X2 e [ k] = [T ] ⎡k ⎤ [T ] ⎪ Y2 ⎪ ⎣ ⎦ ⎩ ⎭x⎧ u1 ⎫ ⎪v ⎪ e ⎪ 1⎪ {Δ} = ⎨ ⎬ ⎪u2 ⎪ ⎪ v2 ⎪ ⎩ ⎭e− cos α − cosα sinα ⎤ 0 2 0 ⎥⎤ 0⎤ ⎧u1 ⎫ 2 ⎡ cos α sin α − sin α 0 ⎥ ⎥ ⎪ ⎢ −− cosα sinα 0⎥ ⎪ vsin α sin α cos α 0 ⎥ ⎪ 1 ⎪ [T ] = ⎢ ⎥ 2 ⎬ ⎨cosα sinα cosα sin ⎥ ⎥⎪ 0− u 2 ⎪ cos α sinα α ⎥ ⎢ 0 cos α 0 ⎥⎥ ⎥ ⎪ 0⎦ ⎪v2 sin2 α ⎢ cosα sin0 − sin α2 α α ⎦ 0 cos ⎥ ⎩− ⎭ α sin ⎣ ⎦2cosα sinα e例：试用后处理法计算图示桁架各杆内力，设各杆EA为常数。