2015届高三数学一轮复习备考试题统计(含答案)

解答题规范专练(三) 数 列1．已知数列{a n }中，a 1＝2，a 2＝4，a n ＋1＝3a n －2a n －1(n ≥2，n ∈N *)．(1)证明数列{a n ＋1－a n }是等比数列，并求出数列{a n }的通项公式；(2)记b n ＝2(a n －1)a n(n ∈N *)，数列{b n }的前n 项和为S n ，求使S n >2 013成立的n 的最小值．2．已知数列{a n }满足a n ＋1＝2a n a n ＋2，且a 1＝2. (1)判断数列⎩⎨⎧⎭⎬⎫1a n 是否为等差数列，若是，请给予证明，若不是，请说明理由； (2)若b n ＝2＋a n a n ·⎝⎛⎭⎫12n ，求数列{b n }的前n 项和T n .3．(2014·皖南八校联考)将数列{a n }中所有的项按每一行比上一行多一项的规则排成如下数表：a 1a 2 a 3a 4 a 5 a 6a 7 a 8 a 9 a 10……记表中的第1列数a 1，a 2，a 4，a 7，…构成的数列为{b n }，b 1＝a 1＝1，S n 为数列{b n }的前n 项和，且满足2b n b n S n －S 2n＝1(n ≥2，n ∈N *)． (1)证明数列⎩⎨⎧⎭⎬⎫1S n 是等差数列，并求数列{b n }的通项公式； (2)上表中，若从第3行起，每一行中的数按从左到右的顺序均构成等比数列，且公比为同一个正数．当a 81＝－491时，求上表中第k (k ≥3)行所有项的和．答 案1．解：(1)证明∵a n ＋1＝3a n －2a n －1(n ≥2，n ∈N *)，∴a n ＋1－a n ＝2(a n －a n －1)(n ≥2，n ∈N *)．∵a 1＝2，a 2＝4，∴a 2－a 1＝2≠0，∴a n －a n －1≠0(n ≥2，n ∈N *)，故数列{a n ＋1－a n }是首项为2，公比为2的等比数列，∴a n ＋1－a n ＝2， ∴a n ＝(a n －a n －1)＋(a n －1－a n －2)＋(a n －2－a n －3)＋…＋(a 2－a 1)＋a 1＝2n －1＋2n －2＋2n －3＋…＋21＋2＝2×(1－2n －1)1－2＋2＝2n (n ≥2，n ∈N *)， 又a 1＝2也满足上式，∴a n ＝2n (n ∈N *)．(2)由(1)知b n ＝2(a n －1)a n ＝2⎝⎛⎭⎫1－1a n ＝2⎝⎛⎭⎫1－12n ＝2－12n －1(n ∈N *)， ∴S n ＝2n －⎝⎛⎭⎫1＋121＋122＋…＋12n －1＝2n －1－12n 1－12＝2n －2⎝⎛⎭⎫1－12n ＝2n －2＋12n －1， 由S n >2 013得，2n －2＋12n －1>2 013，即n ＋12n >2 0152， ∵n ∈N *，∴n ＋12n 的值随n 的增大而增大， ∴n 的最小值为1 008.2．解：(1)数列⎩⎨⎧⎭⎬⎫1a n 是等差数列，理由如下： ∵a n ＋1＝2a n a n ＋2，a n ≠0，∴1a n ＋1＝1a n ＋12， ∴数列⎩⎨⎧⎭⎬⎫1a n 是首项为12，公差为12的等差数列． (2)由(1)知，1a n ＝12＋(n －1)·12＝n 2， b n ＝2＋a n a n ·⎝⎛⎭⎫12n ＝⎝⎛⎭⎫2a n ＋1·⎝⎛⎭⎫12n ＝(n ＋1)·⎝⎛⎭⎫12n ， ∴T n ＝2×12＋3×⎝⎛⎭⎫122＋4×⎝⎛⎭⎫123＋…＋(n ＋1)·⎝⎛⎭⎫12n ，① 12T n ＝2×⎝⎛⎭⎫122＋3×⎝⎛⎭⎫123＋4×⎝⎛⎭⎫124＋…＋(n ＋1)·⎝⎛⎭⎫12n ＋1.② ①－②得12T n ＝1＋⎝⎛⎭⎫122＋⎝⎛⎭⎫123＋…＋⎝⎛⎭⎫12n －(n ＋1)·⎝⎛⎭⎫12n ＋1＝1＋14⎣⎡⎦⎤1－⎝⎛⎭⎫12n －11－12－(n ＋1)⎝⎛⎭⎫12n ＋1＝ 32－n ＋32n ＋1，∴T n ＝3－n ＋32n . 3．解：(1)由已知，当n ≥2时，2b n b n S n －S 2n＝1， 又b n ＝S n －S n －1，所以2(S n －S n －1)(S n －S n －1)S n －S 2n＝1， 即2(S n －S n －1)－S n －1S n＝1，所以1S n －1S n －1＝12. 又S 1＝b 1＝a 1＝1，所以数列⎩⎨⎧⎭⎬⎫1S n 是首项为1，公差为12的等差数列． 故1S n ＝1＋12(n －1)＝n ＋12，即S n ＝2n ＋1. 所以当n ≥2时，b n ＝S n －S n －1＝2n ＋1－2n ＝－2n (n ＋1).因此b n ＝⎩⎪⎨⎪⎧ 1，n ＝1，－2n (n ＋1)，n ≥2.(2)设表中从第3行起，每行的公比都为q ，且q >0.因为1＋2＋…＋12＝12×132＝78， 所以表中第1行至第12行含有数列{a n }中的前78项，故a 81在表中第13行第3列，因此a 81＝b 13·q 2＝－491.又b 13＝－213×14， 所以q ＝2(舍去负值)．记表中第k (k ≥3)行所有项的和为S ，则S ＝b k (1－q k )1－q ＝－2k (k ＋1)·1－2k 1－2＝2k (k ＋1)·(1－2k )(k ≥3)．。

高考数学一轮复习《统计》练习题（含答案）一、单选题1．已知条件p ：11x -<<，q ：x >m ，若p 是q 的充分不必要条件，则实数m 的取值范围是（ ） A ．[)1,-+∞B ．(),1-∞-C ．()1,0-D ．(],1-∞-2．下表为随机数表的一部分：08015 17727 45318 22374 21115 78253 77214 77402 43236 00210 45521 64237已知甲班有60位同学，编号为00~59号，规定：利用上面的随机数表，从第1行第4列的数开始，从左向右依次读取2个数，则抽到的第8位同学的编号是（ ） A ．11B ．15C ．25D ．373．一组数据的方差为()20S S ≥，将该组数据都乘以2，所得到的一组新数据的标准差为（ ）A ．22S B ．SC ．2SD ．2S4．甲、乙两所学校的男女生比例如图所示，已知甲校学生总数为1500，乙校学生总数为1000，下列结论错误的是（ ）A ．甲校女生比乙校女生多B ．乙校男生比甲校男生少C ．乙校女生比甲校男生少D ．甲校女生比乙校男生少5．某校共有学生3000人，为了解学生的身高情况，用分层抽样的方法从三个年级中抽取容量为100的样本，其中高一抽取40人，高二抽取30人，则该校高三学生人数为（ ） A ．600B ．800C ．900D ．12006．设某高中的男生体重y （单位：kg ）与身高x （单位：cm ）具有线性相关关系，根据一组样本数据()(12)i i x y i n =,，，，，用最小二乘法建立的回归方程为ˆ0.8580.71y x =-，则下列结论中不正确的是（ ） A ．y 与x 有正的线性相关关系B ．回归直线过样本点的中心(),x yC ．若该高中某男生身高增加1cm ，则其体重约增加0.85kgD ．若该高中某男生身高为170cm ，则可断定其体重必为63.79kg 7．x 是12100,,,x x x 的平均值，5为4120,,,x x x 的平均值，10为4142100,,,x x x 的平均值，则x =（ ） A ．8B ．9C ．15D ．1528．某学校有男生400人，女生600人．为调查该校全体学生每天睡眠时间，采用分层抽样的方法抽取样本，计算得男生每天睡眠时间均值为7.5小时，方差为1，女生每天睡眠时间为7小时，方差为0.5．若男、女样本量按比例分配，则可估计总体方差为（ ）． A ．0.45B ．0.62C ．0.7D ．0.769．某样本点)()(,1,2,,i i x y i n =⋅⋅⋅的经验回归方程为ˆ0.50.7yx =+，当8x =时，y 的实际值为4.5，则当8x =时，预测值与实际值的差值为（ ）． A ．0.1B ．0.2C ．0.3D ．0.410．若数据9，m ，6，n ，5的平均数为7，方差为2，则数据11，9，21m -，17，21n -的平均数和方差分别为（ ） A ．13，4B ．14，4C ．13，8D ．14，811．2021年起，我市将试行“3+1+2”的普通高考新模式，即除语文、数学、外语3门必选科目外，考生再从物理、历史中选1门，从化学、生物、地理、政治中选2门作为选考科目.为了帮助学生合理选科，某中学将高一每个学生的六门科目综合成绩按比例均缩放成5分制，绘制成雷达图.甲同学的成绩雷达图如图所示，下面叙述一定不正确的是（ ）A ．甲的化学成绩领先年级平均分最多.B ．甲有2个科目的成绩低于年级平均分.C ．甲的成绩最好的前两个科目是化学和地理.D ．对甲而言，物理、化学、地理是比较理想的一种选科结果.12．冬末春初，乍暖还寒，人们容易感冒发热，若发生群体性发热，则会影响到人们的身体健康，干扰正常工作生产，某大型公司规定：若任意连续7天，每天不超过5人体温高于37.3℃，则称没有发生群体性发热，下列连续7天体温高于37.3℃人数的统计特征数中，能判定该公司没有发生群体性发热的为（ ）（1）中位数为3，众数为2 （2）均值小于1，中位数为1（3）均值为3，众数为4 （4）均值为2 A ．（1）（3）B ．（3）（4）C ．（2）（3）D ．（2）（4）二、填空题13．某校高一、高二、高三年级的学生人数之比为5:5:4，现按年级用分层抽样的方法抽取若干人，若抽取的高三年级的学生人数为20，则抽取的样本容量为______.14．已知具有线性相关的变量x 、y ，设其样本点为()(1,2,,,8)i i i A x y i =，回归直线方程为1ˆ2yx b =+，若128(6,2)OA OA OA +++=(O 为原点），则b =_______.15．已知一组数据按顺序排列为：12，16，20，n ，46，51，58，60.若这组数据的第30百分位数的两倍与这组数据的第50百分位数相等，则n 的值为___________.16．某工厂为了对新研发的一种产品进行合理定价，将该产品按事先拟定的价格进行试销，得到如下数据：由表中的数据得线性回归方程为y bx a =+，其中20b =-，预测当产品价格定为9.5(元)时，销量约为__________件．三、解答题17．某区政府组织了以“不忘初心，牢记使命”为主题的教育活动，为统计全区党员干部一周参与主题教育活动的时间，从全区的党员干部中随机抽取n 名，获得了他们一周参与主题教育活动时间（单位：h ）的频率分布直方图如图所示，已知参与主题教育活动时间在(]12,16内的人数为92．(1)求n 的值；(2)以每组数据所在区间的中点值作为本组的代表，估算这些党员干部参与主题教育活动时间的中位数（中位数精确到0.01）．(3)如果计划对参与主题教育活动时间在(]16,24内的党员干部给予奖励，且在(]16,20，(]20,24内的分别评为二等奖和一等奖，那么按照分层抽样的方法从获得一、二等奖的党员干部中选取5人参加社区义务宣讲活动，再从这5人中随机抽取2人作为主宣讲人，求这2人均是二等奖的概率．18．由于疫情影响，今年我们学校开展线上教学，高一年级某班班主任为了了解学生上网学习时间，对本班40名学生某天上网学习时间进行了调查，将数据（取整数）整理后，绘制出如图所示频率分布直方图，已知从左到右各个小组的频率分别是0.15，0.25，0.35，0.20，0.05，则根据直方图所提供的信息：（1）这一天上网学习时间在100~119分钟之间的学生有多少人？（2）估计这40位同学的线上平均学习时间（同一组中的数据用该组区间的中点值为代表）以及中位数分别是多少？（精确到0.1）（3）如果只用这40名学生这一天上网学习时间作为样本去推断该校高一年级全体学生该天的上网学习时间，这样推断是否合理？为什么？19．省政府坚持以习近平新时代中国特色社会主义思想为指导，落实全国、全省教育大会部署，坚持社会主义办学方向，落实立德树人根本任务，发展素质教育，推进育人方式变革，引导全社会树立科学的教育质量观和人才培养观，切实减轻有损中小学生身心健康的过重学业负担，遵循教育教学规律，促进中小学生健康成长，培养德智体美劳全面发展的社会主义建设者和接班人．从某市抽取1000名一年级小学生进行调查，统计他们每周做作业的时长（单位：小时），根据结果绘制的频率分布直方图如下：（1）根据频率分布直方图，求所有被抽查小学生每周做作业的平均时长和中位数；（同一组中的数据用该组区间的中点值作代表）（2）①为了进一步了解，现采用分层抽样的方法从[8,10]和[10,12]组中抽取50名学生，则两组各抽取多少人？②再利用分层抽样从抽取的50人中选5人参加一个座谈会．现从参加座谈会的5名学生中随机抽取两人发言，求[8,10]小组中恰有2人发言的概率？20．为了调查某地区高中女生的日均消费情况，研究人员随机抽取了该地区5000名高中女生作出调查，所得数据统计如下图所示．(1)求a 的值以及这5000名高中女生的日均消费的平均数（同一组数据用该组区间的中间值代替）；(2)在样本中，现按照分层抽样的方法从该地区消费在[)15,20与[)20,25的高中女生中随机抽取9人，若再从9人中随机抽取3人，记这3人中消费在[)15,20的人数为X ，求X 的分布列以及数学期望．21．道德与法律的联系：法律､道德都是行为规范，都是为规范人们的行为而规定的行动准则.1.法律需要道德的奠基和撑持；2.道德的实施需要法律的强制保障.某校进行了一次道德与法律的相关测试（满分：100分），并随机抽取了50个统计其分数，得到的结果如下表所示： 成绩/分 [)0,20[)20,40[)40,60[)60,80[)80,100人数/个 44102210(1)若同一组数据用该区间中点值作代表，试估计这次测试的平均分和中位数（所得结果四舍五入保留整数）；(2)假设处于[)20,40的4个人的成绩分别为20，26，35，38，求表中成绩的10%分位数； (3)以频率估计概率，若在这个学校中，随机挑选3人，记3人的成绩在[)80,100间的数量为随机变量X ，求X 的分布列和数学期望()E X .22．某校从高三年级学生中随机抽取100名学生的某次数学考试成绩，将其成绩分成[)50,60，[)60,70，[)70,80，[)80,90，[]90,100的5组，制成如图所示的频率分布直方图.(1)求图中x 的值；(2)估计这组数据的平均数；(3)若成绩在[)50,60内的学生中男生占40%.现从成绩在[)50,60内的学生中随机抽取2人进行分析，求2人中恰有1名女生的概率.23．某校从高三学生中选取了50名学生参加数学质量检测，成绩（单位：分）分组及各组的频数如下：[40,50)，2；[50,60)，3；[60,70)，10；[70,80)，15；[80,90)，12；[90,100]，8．(1)列出频率分布表；(2)画出频率直方图及频率折线图．24．某农业科学研究所为检验某农作物种子的培育有效率，进行了如下试验：一是对该农作物的10000粒种子进行培育，发现有20粒种子未发芽；二是将未进行培育的该农作物的2500粒种子种植在5块试验田中，各试验田种植的种子数及未发芽数如下表：（1）求y 关于x 的回归直线方程； （2）在上述试验下，若以1nN-表示该农作物种子的培育有效率，其中n 为进行培育的10000粒种子的未发芽数，N 为依据上述回归方程估算的未进行培育的10000粒种子的未发芽数，请估计该农作物种子的培育有效率（结果保留3位有效数字）．参考公式；在回归方程ˆˆˆy bx a =+中，1221ˆni ii nii x y nx ybxnx==-⋅=-∑∑，ˆˆa y bx=-参考答案1．D2．A3．D4．D5．C6．D7．A8．D9．B10．C11．A12．D 13．7014．18-##-0.12515．34 16．6017．（1）由已知可得，0.25(0.02500.04750.05000.0125)0.1150a =-+++=． 则0.1150492n ⨯⨯=，得922000.11504n ==⨯．（2）设中位数为x ，则0.050040.01254(16)0.11500.5x ⨯+⨯+-⨯=，得13.83x ≈．（3）按照分层抽样的方法从(16，20]内选取的人数为0.050540.05000.0125⨯=+，从(20，24]内选取的人数为0.0125510.05000.0125⨯=+．记二等奖的4人分别为a ，b ，c ，d ，一等奖的1人为A ，事件E 为“从这5人中抽取2人作为主宣讲人，且这2人均是二等奖”．从这5人中随机抽取2人的基本事件为(,)a b ，(,)a c ，(,)a d ，(,)a A ，(,)b c ，(,)b d ，(,)b A ，(,)c d ，(,)c A ，(,)d A ，共10种，其中2人均是二等奖的情况有(,)a b ，(,)a c ，(,)a d ，(,)b c ，(,)b d ，(,)c d ，共6种， 由古典概型的概率计算公式得()63105P E ==． 18．（1）因为频数=样本容量⨯频率，一天上网学习时间在100119分钟之间的学生所占频率为0.35，所以一天上网学习时间在100~119分钟之间的学生人数为400.3514⨯=（人） （2）40位同学的线上学习时间估计值为：0.1569.90.2589.90.35109.90.20129.90.05149.9104.9⨯+⨯+⨯+⨯+⨯=分钟在中位数左边和右边的小长方形的面积和是相等的，设在99.9~119.9靠近左侧长度为x ,则0.15+0.25+0.350.5x =解得0.27x ≈； 所以中位数估计值是99.9+0.27=100.17100.2≈（3）因为该样本的选取只在高一某班，不具有代表性，所以这样推断不合理. 19．（1）设抽查学生做作业的平均时长为x ，中位数为y ，0.0510.130.2550.370.1590.1110.0513 6.8x =⨯+⨯+⨯+⨯+⨯+⨯+⨯=， 0.050.10.250.15(6)0.5y y =+++⨯-=，解得203y =即抽查学生做作业的平均时长为6.8，中位数为203． （2）①[8,10]组的人数为10000.15150⨯=人，设抽取的人数为a ，[]10,12组的人数为10000.1100⨯=人， 设抽取的人数为b ，则50150100250a b ==，解得30a =，20b = 所以在[8,10]和[]10,12两组中分别抽取30人和20人，②再抽取5人，其中[8,10]和[]10,12两组中分别抽取3人和2人，将[8,10]组中被抽取的工作人员标记为1A ，2A ，3A ，将[]10,12中的标记为1B ，2B ． 设事件C 表示从[8,10]小组中恰好抽取2人，则抽取的情况如下：{}12,A A ，{}13,A A ，{}11,A B ，{}12,A B ，{}23,A A ，{}21,A B ，{}22,A B ，{}31,A B ，{}32,A B ，{}12,B B 共10种情况；其中在[8,10]中恰好抽取2人有3种，则3()10P C =． 20．（1）由题意得，()20.040.080.0651a +++⨯=，解得0.01a =，故所求平均数为17.50.427.50.332.50.0537.50.0524.25⨯0.2+22.5⨯+⨯+⨯++=（元）； （2）由题意得，消费在[)15,20，[)20,25的高中女生分别有3人和6人，故X 的可能取值为0，1，2，3，∴()6033395021C C P X C ===，()21633915128C C P X C ===，()1263393214C C P X C ===，()0363391384C C P X C ===， 故X 的分布列为：∴()515310123121281484E X =⨯+⨯+⨯+⨯=； 故答案为：1. 21．(1)估计这次测试的平均分为1043045010702290106250x ⨯+⨯+⨯+⨯+⨯==（分）；设这次测试的中位数为0x ，显然()060,80x ∈，则060441022200.550x -+++⋅=，解得066x ≈（分）. 即估计这次测试的中位数为66.(2)由于5010%5⨯=，所以表中成绩的10%分位数为2026232+=. (3)X 所有可能取值为0，1，2，3.由表中数据可知，任意挑选一人，成绩在[)80,100间的概率为101505=. 所以()346405125P X ⎛⎫=== ⎪⎝⎭，()21341481C 55125P X ⎛⎫=== ⎪⎝⎭， ()122341122C 55125P X ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭，()31135125P X ⎛⎫=== ⎪⎝⎭， 故X 的分布列为故X 的数学期望()6448121301231251251251255E X =⨯+⨯+⨯+⨯=. 22．(1)由频率分布直方图得()0.0050.0350.0300.010101x ++++⨯=，解得0.020x =， 所以图中x 的值是0.020.(2)由频率分布直方图得这组数据的平均数： (550.005650.020750.03585x =⨯+⨯+⨯+⨯)0.030950.0101077+⨯⨯=， 所以这组数据的平均数为77.(3)数学成绩在[)50,60内的人数为0. 005101005⨯⨯=(人)，其中男生人数为540%2⨯=(人)，则女生人数为3人，记2名男生分别为1A ，2A ，3名女生分别为1B ，2B ，3B ，从数学成绩在[)50,60内的5人中随机抽取2人进行分析的基本事件为：121112132122A A A B A B A B A B A B ,,,,,,23121323A B B B B B B B ,,,，共10个不同结果，它们等可能， 其中2人中恰有1名女生的基本事件为111213212223,,,,,A B A B A B A B A B A B ，共6种结果， 所以2人中恰有1名女生的概率为为63105=. 23．（1）解：频率分布表如下：（2） 频率直方图及频率折线图如图所示．24． (1)依题意，3004005006007005005x ++++==，2466755y ++++==， 513002400450066006700713700ii i x y ==⋅+⋅+⋅+⋅+⋅=∑， 52222221(34567)100001350000i i x==++++⋅=∑， 于是得512252113700550051200ˆ0.01213500005500100000i ii i i x y nx y b x nx==-⋅-⋅⋅====-⋅-∑∑，ˆˆ50.0125001ay bx =-=-⨯=-， 所以y 关于x 的回归直线方程为ˆ0.0121yx =-； (2)由(1)知，估计未进行培育的10000粒种子的未发芽数N 约为：ˆ0.012100001119y =⨯-=，而已培育的10000粒种子有20粒种子未发芽，即20n =， 所以该农作物种子的培育有效率为209910832119119-=≈。

2015届高三一轮复习测试卷三文科数学考查范围：集合、逻辑、函数、导数、复数 时间：2014年6月19日第Ⅰ卷2．集合{}2|20A x x x =+-≤,B ={}0x x <,则AB =（ ）A ．[)2,0-B ．(,1]-∞C ．[1,2]D ．[1,)+∞3．函数1lg(2)y x =-的定义域是（ ）A. []12，B. [)12，C. ()12，D. (]12，4．已知幂函数)(x f y =的图象经过点，则1()9f 的值为( )A ．3B ．13C ．18D ．145．已知()1+x f =x x 62+，则()x f 的表达式是（ ）A ．542-+x x B ．782++x x C ．522-+x x D ．1062-+x x6．定义在R 上的偶函数f (x )，对任意x 1，x 2∈[0，＋∞)(x 1≠x 2)，有f (x 2)－f (x 1)x 2－x 1>0，则( )．A ．f (3)<f (－2)<f (1)B ．f (1)<f (－2)<f (3)C ．f (－2)<f (1)<f (3)D ．f (3)<f (1)<f (－2)7．设a ＝20.4，b ＝0.43，c ＝4log 0.3，则a ，b ，c 的大小关系为( )．A ．a <b <cB ．b <c <aC ．c <a < bD ．a <c <b 8. 函数3()233f x x x =+-的零点所在的区间为( )A ．(-1,0)B ．( 0,1)C ．(1,2)D ．(2,3) 9.已知)1('),1('3)(2f xf x x f 则+==（ ）A ．-1B ．0C ．1D ．210.已知函数()f x 的导函数()f x '的图象如图所示，那么函数()f x 的图象最有可能的是（ ）11. 已知函数f (x )＝x 3＋ax 2＋(a ＋6)x ＋1有极大值和极小值，则实数a 的取值范围是( )．A ．[－1,2]B ．(－∞，－3)∪(6，＋∞)C ．[－3,6]D ．(－∞，－1)∪(2，＋∞)12.已知函数()y f x =的周期为2,当[1,1]x ∈-时2()f x x =,那么函数()y f x =的图象与函数5log y x =的图象的交点共有( )A.2个B.4个C.6个D.8个第Ⅱ卷二、填空题：本大题共4小题，每小题4分，共16分.将答案填在答题卷相应位置上.13．已知函数y ＝loga (x ＋b )的图象如图所示， 则a +b ＝________.14．已知2x ＝3y＝6，则1x ＋1y＝________.15．设函数()2sin 1f x x x =+,若()10f a =,则()f a -= .16．函数f (x )＝|log 3 x |在区间[a ，b ]上的值域为[0,1]，则b －a 的取值范围为三、解答题(本大题共6小题，满分74分．解答须写出文字说明、证明过程和演算步骤.) 17. (本题满分l2分)计算：(1) )121023170.0272179--⎛⎫⎛⎫--+- ⎪ ⎪⎝⎭⎝⎭(2) lg 2lg 50＋lg 5lg 20－lg100lg 5lg 2；18．（本小题满分12分）记函数()f x =的定义域为集合A ，函数()()lg 12x g x =-的定义域为集合B ．（1）求集合B ；（2）若A B A =，求实数a 的取值范围．19．（本小题满分12分）已知函数f (x )＝ax 2＋23x ＋b是奇函数，且f (2)＝53.(1)求实数a ，b 的值；(2)求函数f (x )在(－∞，0)上的极值．20. （本小题满分12分)已知函数)()(2R a ax e x f x∈-=.（Ⅰ）求函数)(x f 在点()0,1P 处的切线方程；（Ⅱ）若函数)(x f 为()0,+∞上的单调递增函数，试求a 的取值范围.21．（本小题满分12分)某化工厂引进一条先进生产线生产某种化工产品，其生产的总成本y (万元)与年产量x (吨)之间的函数关系式可以近似地表示为y ＝x 25－48x ＋8 000，已知此生产线年产量最大为210吨．(1)求年产量为多少吨时，生产每吨产品的平均成本最低，并求最低成本；(2)若每吨产品平均出厂价为40万元，那么当年产量为多少吨时，可以获得最大利润？最大利润是多少？22．（本小题满分14分)已知函数2()ln(1)()f x x ax a x a =---∈R ． (1) 当1a =时，求函数()f x 的最值； (2) 求函数()f x 的单调区间；(3) 试说明是否存在实数(1)a a ≥使()y f x =的图象与5ln 28y =+无公共点．答案：DACBA BCBAA BD 13．6； 14．1； 15．-8； 16．28,33⎡⎤⎢⎥⎣⎦17．(1)-45;(2)118．（本小题满分12分）记函数()f x =的定义域为集合A ，函数()()lg 12x g x =-的定义域为集合B ．（1）求集合B ；（2）若A B A =，求实数a 的取值范围． 解：（1）由已知得：{}{}|120|0x B x x x =->=<（2）由已知得：()(){}{}|0|1111A x x x a x x a a x a ==-+--≥≤-≥+或 ∵ AB A =B A ∴⊆， 10a ∴-≥所以，实数a 的取值范围为[)1,+∞19．（本小题满分12分）已知函数f (x )＝ax 2＋23x ＋b是奇函数，且f (2)＝53.(1)求实数a ，b 的值；(2)求函数f (x )在(－∞，0)上的极值．解 (1)即a ＝2，b ＝0，此时f (x )＝2x 2＋23x.(2)由(1)知f (x )＝2x 2＋23x ＝23x ＋23x，f (x )在(－∞，－1]上是增函数，在(－1,0)上是减函数，所以，f (x )在1x =-取得极大值为()413f -=-，无极小值.20. （本小题满分12分)已知函数)()(2R a ax e x f x ∈-=.（Ⅰ）求函数)(x f 在点()0,1P 处的切线方程；（Ⅱ）若函数)(x f 为()0,+∞上的单调递增函数，试求a 的取值范围.解：（Ⅰ）ax e x f x2)(-=' ，(0)1f '∴=…………………3分所以)(x f 在点)1,0(P 处的切线方程为x f f y )0()0('=-，即1+=x y .……6分 （Ⅱ）由题意02)(≥-='ax e x f x 恒成立………………7分因为0>x ，所以x e a x ≤2，令x e x g x=)(，则2)1()(x x e x g x -='，由0)(='x g 得1=x ，1>x 时0)(>'x g ，1<x 时0)(<'x g .e g x g ==∴)1()(min ,2ea ≤∴；…………… 10分 综上，若函数)(x f 为R 上的单调递增函数，则20ea ≤<.………………12分21．（本小题满分12分)某化工厂引进一条先进生产线生产某种化工产品，其生产的总成本y (万元)与年产量x (吨)之间的函数关系式可以近似地表示为y ＝x 25－48x ＋8 000，已知此生产线年产量最大为210吨．(1)求年产量为多少吨时，生产每吨产品的平均成本最低，并求最低成本；(2)若每吨产品平均出厂价为40万元，那么当年产量为多少吨时，可以获得最大利润？最大利润是多少？解： (1)每吨平均成本为y x (万元)．则（方法一）y x ＝x 5＋8 000x －48)0(>x ，----2分设4880005)(-+=x x x f ，2800051)(xx f -='， 令2800051)(xx f -='=0，得x ＝200（舍去负值），----4分 )200,0(∈x 时，0)(<'x f ，),200(+∞∈x 时，0)(>'x f ，)(x f ∴在x ＝200处取得极小值也是最小值--------5分∴年产量为200吨时，每吨平均成本最低为32万元．------6分 （方法二） y x ＝x 5＋8 000x－48≥2 x 5·8 000x－48＝32，)0(>x -------4分 当且仅当x 5＝8 000x，即x ＝200时取等号．---------5分∴年产量为200吨时，每吨平均成本最低为32万元．------6分 (2)设年获得总利润为R (x )万元， 则R (x )＝40x －y ＝40x －x 25＋48x －8 000＝－x 25＋88x －8 000＝－15(x －220)2＋1 680(0≤x ≤210)．------9分∵R (x )在[0,210]上是增函数，∴x ＝210时，R (x )有最大值为 －15(210－220)2＋1 680＝1 660.--------11分 ∴年产量为210吨时，可获得最大利润1 660万元．-----12分22．（本小题满分14分)已知函数2()ln(1)()f x x ax a x a =---∈R ． (1) 当1a =时，求函数()f x 的最值； (2) 求函数()f x 的单调区间；(3) 试说明是否存在实数(1)a a ≥使()y f x =的图象与5ln 28y =+无公共点． 解：（1） 函数2()ln(1)()f x x ax a x a =---∈R 的定义域是()1,+∞．当1a =时，'32()12()2111x x f x x x x -=--=--，所以()f x 在3(1,)2为减函数 ,在3(,)2+∞为增函数，所以函数f (x )的最小值为3()2f =3ln 24+． (2) '22()2()2,11a x x a f x x a x x +-=--=-- 若0a ≤时，则21,2a +≤f '(x )22()21a x x x +-=-0>在()1,+∞恒成立， 所以()f x 的增区间为()1,+∞．若0a >，则21,2a +>故当21,2a x +⎛⎤∈ ⎥⎝⎦，'()f x 22()21a x x x +-=-0≤， 当2,2a x +⎡⎫∈+∞⎪⎢⎣⎭时，f (x ) 22()21a x x x +-=-0≥, 所以0a >时()f x 的减区间为21,2a +⎛⎤ ⎥⎝⎦，()f x 的增区间为2,2a +⎡⎫+∞⎪⎢⎣⎭． (3) 1a ≥时，由（2）知()f x 在()1,+∞上的最小值为22()1ln 242a a af a +=-+-， 由2()()2ag a f +=21ln 42a aa =-+-在 [)1,+∞上单调递减， 所以max 3()(1)ln 2,4g a g ==+则max 51()(ln 2)88g a -+=0>， 因此存在实数()1a a ≥使()f x 的最小值大于5ln 28+，故存在实数()1a a ≥使()y f x =的图象与5ln 28y =+无公共点．。

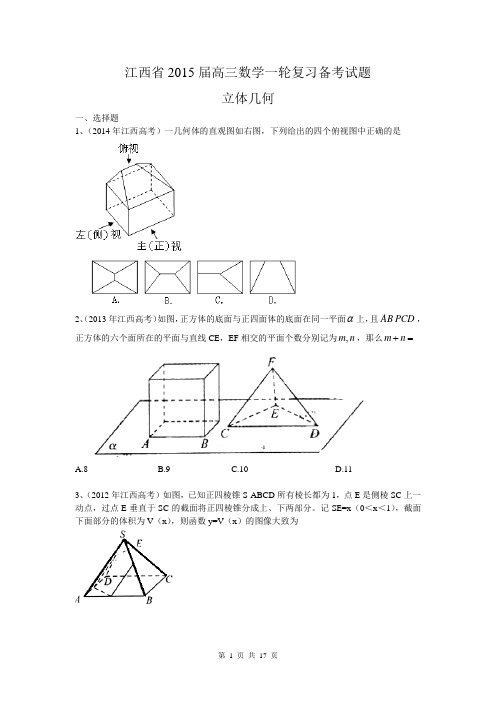
江西省2015届高三数学一轮复习备考试题立体几何一、选择题 1、（2014年江西高考）一几何体的直观图如右图，下列给出的四个俯视图中正确的是2、（2013年江西高考）如图，正方体的底面与正四面体的底面在同一平面α上，且AB CD ，正方体的六个面所在的平面与直线CE ，EF 相交的平面个数分别记为,m n ，那么m n +=A.8B.9C.10D.11 3、（2012年江西高考）如图，已知正四棱锥S-ABCD 所有棱长都为1，点E 是侧棱SC 上一动点，过点E 垂直于SC 的截面将正四棱锥分成上、下两部分。

记SE=x （0＜x ＜1），截面下面部分的体积为V （x ），则函数y=V （x ）的图像大致为4、（红色六校2015届高三第一次联考）已知正方体被过一面对角线和它对面两棱中点的平面截去一个三棱台后的几何体的主（正）视图和俯视图如下，则它的左（侧）视图是( )5、（2014届江西省高三4月模拟）已知某几何体的三视图如图所示，则该几何体的体积为A.233B.223C.203D.1436、（吉安一中2014届高三下学期第一次模拟）如图，正四面体ABCD 的顶点A ，B ，C 分别在两两垂直的三条射线,,Ox Oy Oz 上，则在下列命题中，错误．．的为（ ）A. O-ABC 是正三棱B. 直线OB ∥平面ACDC. 直线AD 与OB 所成的角是45°D. 二面角D-OB-A 为45°7、（南昌三中2014届高三第七次考试）M 是正方体1111ABCD A B C D -的棱1DD 的中点，给出下列命题：①过M 点有且只有一条直线与直线AB 、11B C 都相交； ②过M 点有且只有一条直线与直线AB 、11B C 都垂直； ③过M 点有且只有一个平面与直线AB 、11B C 都相交；④过M 点有且只有一个平面与直线AB 、11B C 都平行.其中真命题是（ ） A ．②③④ B ．①③④ C ．①②④ D ．①②③ 8、设a ，b 是不同的直线，α，β是不同的平面，则下列命题：①若a ⊥b ，a ⊥α，则b ∥α； ②若a ∥α，α⊥β则a ⊥β； ③若a ⊥β，α⊥β，则a ∥α；④若a ⊥b ，a ⊥α，b ⊥β则a ⊥β． 其中正确命题的个数是A ．0B ．1C ．2D ．39、将正方体(如图(a)所示)截去两个三棱锥，得到图(b)所示的 几何体，则该几何体的侧视图为10、设m 、n 是两条不同的直线，α、β是两个不同的平面，考查下列命题，其中正确的命题是A 、n n αβαβ⊥,⇒⊥∥,m ∥mB 、,,m n m n αβαβ⊥⊂⊥⇒⊥C 、,,m n m n αβαββ⊥=⊥⇒⊥ D 、,,m n n αβαβ⊥⊥⇒⊥∥m11、平面四边形ABCD 中，1===CD AD AB ，CD BD BD ⊥=,2，将其沿对角线BD 折成四面体BCD A -'，使平面⊥BD A '平面BCD ，若四面体BCD A -'顶点在同一个球面上，则该球的体积为( )A.π23 B. π3 C. π32 D. π2 12、如右图所示是一个几何体的三视图，则该几何体的体积为( )A ．1B ．12C ．34D ．32二、解答题1、（2014年江西高考）如图，四棱锥ABCD P -中，ABCD 为矩形，平面⊥PAD 平面ABCD .（1）求证：;PD AB ⊥ （2）若,2,2,90===∠PC PB BPC 问AB 为何值时，四棱锥ABCD P -的体积最大？并求此时平面PBC 与平面DPC 夹角的余弦值.2、（2013年江西高考）如图，四棱锥P ABCD -中，PA ,ABCD E BD ⊥平面为的中点，G PD 为的中点，3,12DAB DCB EA EB AB PA ∆≅∆====，，连接CE 并延长交AD 于F .(1) 求证：AD CFG ⊥平面；(2)求平面BCP 与平面DCP 的夹角的余弦值.3、（2012年江西高考）在三棱柱ABC-A 1B 1C 1中，已知AB=AC=AA 1BC=4，在A 1在底面ABC 的投影是线段BC 的中点O 。

浙江省宁波市2015届高三一轮复习阶段性考试数学理试题本试题卷分选择题和非选择题两部分．全卷共4页, 选择题部分1至2页, 非选择题部分3至4页．满分150分, 考试时间120分钟．请考生按规定用笔将所有试题的答案涂、写在答题纸上．第Ⅰ卷（选择题部分 共50分）一、选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的． 1．设集合M ={x |1122x -<<}，N ={x | x 2 ≤ x }，则M ∩N = （A ）1[1,)2- （B ）1(,1]2-（C ）1[0,)2 （D ）1(,0]2-2．设a ＞1＞b ＞0，则下列不等式中正确的是 （A ）(-a )7＜(-a )9 （B ）b - 9＜b - 7（C ）11lg lg a b > （D ）11ln ln a b>3．已知R α∈，cos 3sin αα+，则tan 2α=（A ）43 （B ）34 （C ）34- （D ）43-4．若某程序框图如图所示，则输出的n 的值是（A ）3 （B ）4 （C ）5 （D ）6(第4题图)5．设,m n 是两条不同的直线，,αβ是两个不同的平面，则下列命题中正确．．的是 （A ）若//,m n αβ⊥且αβ⊥，则m n ⊥ （B ）若,m n αβ⊥⊥且m n ⊥，则αβ⊥ （C ）若/,/n m αβ⊥且n β⊥，则//m α （D ）若,m n αβ⊂⊂且//m n ，则//αβ6．已知某锥体的三视图（单位：cm ）如图所示，则该锥体的体积为 （A ）23cm （B ）43cm （C ）63cm （D ）83cm 7．251(1)(2)x x--的展开式的常数项是（A ）48 （B ）﹣48 （C ）112 （D ）﹣1128．袋子里有3颗白球，4颗黑球，5颗红球．由甲、乙、丙三人依次各抽取一个球，抽取后不放回．若每颗球被抽到的机会均等，则甲、乙、丙三人所得之球颜色互异的概率是 （A ）14 （B ）13 （C ）27 （D ）3119．已知实系数二次函数()f x 和()g x 的图像均是开口向上的抛物线，且()f x 和()g x 均有两个不同的零点．则“()f x 和()g x 恰有一个共同的零点”是“()()f x g x +有两个不同的零点”的（A ）充分不必要条件 （B ）必要不充分条件 （C ）充分必要条件（D ）既不充分也不必要条件10．设F 1、F 2是椭圆Γ的两个焦点，S 是以F 1为中心的正方形，则S 的四个顶点中能落在椭圆Γ上的个数最多有（S 的各边可以不与Γ的对称轴平行）（A ）1个 （B ）2个 （C ）3个 （D ）4个（第6题图）正视图侧视图俯视图第Ⅱ卷（非选择题部分 共100分)二、填空题：本大题共7小题, 每小题4分, 共28分． 11．已知复数z 满足22z z +-= i （其中i 是虚数单位），则z = ▲ ． 12．设25z x y =+，其中实数,x y 满足68x y ≤+≤且20x y -≤-≤，则z 的取值范围是▲ ．13．已知抛物线23x y =上两点,A B 的横坐标恰是方程2510x x ++=的两个实根，则直线AB 的方程是 ▲ ．14．口袋中装有大小质地都相同、编号为1，2，3，4，5，6的球各一只．现从中一次性随机地取出两个球，设取出的两球中较小的编号为X ，则随机变量X 的数学期望是 ▲ ．15．已知直线10x y --=及直线50x y --=截圆C 所得的弦长均为10，则圆C 的面积是 ▲ ．16．在△ABC 中，∠C=90︒，点M 满足3BM MC =，则sin ∠BAM 的最大值是 ▲ ． 17．已知点O 是△ABC 的外接圆圆心，且AB=3，AC=4．若存在非零实数．．．．x 、y ，使得AO x AB y AC =+，且21x y +=，则cos ∠BAC = ▲ ．三、解答题：本大题共5小题，共72分．解答应写出文字说明、证明过程或演算步骤． 18．（本题满分14分） 在ABC ∆中，内角,,A B C 的对边分别为,,a b c ，且sin 5B c =，11cos 14B =．（I ）求角A 的大小；（II ）设BC 边的中点为D ，AD =ABC ∆的面积． 19．（本小题满分14分）设等差数列{}n a 的前n 项和为n S ，且248,40a S ==错误！未找到引用源。

江西省2015届高三数学一轮复习备考试题不等式一、选择题1、（2014年江西高考）对任意,x y R ∈,111x x y y -++-++的最小值为 A.1 B.2 C.3 D.42、（2013年江西高考）在实数范围内，不等式211x --≤的解集为3、（2012年江西高考）在实数范围内，不等式|2x-1|+|2x+1|≤6的解集为___________。

4、（崇义中学2015届高三上学期第一次月考）设变量x ，y 满足|3|2,43:y x z x y x xy -=⎪⎩⎪⎨⎧-≥≤+≥则的最大值为( ) A ．8B ．3C ．413 D ．29 5、（红色六校2015届高三第一次联考）若关于x 的不等式21321x x a a -+-≤--在R 上的解集为∅，则实数a 的取值范围是（ ）A.13a a <->或B.03a a <>或C.13a -<<D.13a -≤≤ 6、（崇义中学2015届高三上学期第一次月考）已知不等式组⎩⎪⎨⎪⎧x ≤1，x ＋y ＋2≥0，kx －y ≥0表示的平面区域为Ω，其中k ≥0，则当Ω的面积最小 时的k 为________7、（乐安一中2015届高三上学期开学考试）定义在R 上的函数)(x f 满足1)1(=f ，且对任意R x ∈都有21)(<'x f ，则不等式21)(22+>x x f 的解集为（ ）A.(1，2)B.(0，1)C.),1(+∞D.(-1，1)8、（南昌三中2015届高三上学期第一次月考）若不等式4)2(2)2(2<-+-x a x a 的解集为R ,则实数a 的取值范围是9、（2014届江西省高三4月模拟）若不等式组10100x y x y y +-≤⎧⎪-+≥⎨⎪≥⎩表示的平面区域内的点都不．在圆2221()(0)2x y r r +-=>外，则r 的最小值是________10、（吉安一中2014届高三下学期第一次模拟）已知10a b c >>>>，对以下不等式①a b c c > ②11a bc c > ③11abc c ⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝⎭④1111abc c ⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝⎭⑤11log log c c a b>， 其中成立的是（ ） A. ①②⑤B. ②③④C. ②③⑤D. ③④⑤11、（南昌三中2014届高三第七次考试）设01,a b <<<则下列不等式成立的是( )A ．33a b >B ．11a b< C ．1b a >D ．()lg 0b a -<12、（南昌铁路一中2014届高三第二轮复习测试）不等式2|3||1|3x x a a +--≤-对任意实数x 恒成立,则正实数a 的取值范围______13、（上饶市2014届高三1月第一次高考模拟）若正数,x y 满足230x y +-=，则的最小值为14、设变量,x y 满足10,020,015,x y x y y -≤⎧⎪≤+≤⎨⎪≤≤⎩则23x y +的最大值为 ( ).A 20 .B 35 .C 45 .D 5515、已知变量,x y 满足1,2,0.x y x y ≥⎧⎪≤⎨⎪-≤⎩则x y +的最小值是A. 2B. 3C. 4D. 516、若R c b a ∈,,，b a >，则下列不等式成立的是 （ ）A ．b a 11< B ．1122+>+c bc a C ．22b a > D ．c b c a > 17、已知正数,x y 满足20x y xy +-=，则2x y +的最小值为（A ）8 （B ）4 （C ）2 （D ）0 18、已知011<<ba ，给出下列四个结论：①b a < ②ab b a <+ ③||||b a > ④2b ab < 其中正确结论的序号是A ．①②B ．②④C ．②③D ．③④19、设a,b 是两个实数，且a ≠b ，①,322355b a b a b a +>+②)1(222--≥+b a b a ，③2>+abb a 。

江西省2015届高三数学一轮复习备考试题三角函数一、选择、填空题1、（2014年江西高考）在ABC ∆中，内角A,B,C 所对的边分别是,,,c b a ，若,3,6)(22π=+-=C b a c 则ABC ∆的面积是A.3B.239 C.233 D.332、（2013年江西高考）函数2sin 2y x x =+的最小正周期为T 为3、（2012年江西高考）若tan θ+1tan θ=4,则sin2θ= A ．15 B. 14 C. 13 D. 124、（红色六校2015届高三第一次联考）函数()sin()f x A x ωϕ=+（其中A ＞0，ϕ＜π2的图象如图所示，为了得到()sin 3g x x =的图象，只需将()f x 的图象( )A.右平移π4个单位长度 B.左平移π4个单位长度C.右平移π12个单位长度D.左平移π12个单位长度5、（井冈山中学2015届高三第一次月考）定义在R 上的偶函数()f x 满足(2)()f x f x -=，且在[3,2]--上是减函数，,αβ是钝角三角形的两个锐角， 则(sin )f α与(cos )f β的大小关系是A ．(sin )(cos )f f αβ> B ．(sin )(cos )f f αβ< C ．(sin )(cos )f f αβ= D ．(sin )(cos )f f αβ≥6、（南昌二中2015届高三上学期第一次考）已知,135)4sin(-=+πx 则x 2sin 的值等于 ( ) A ．169120 B ．169119 C ．169120- D ．119169-7、（南昌市八一中学2015届高三8月月考）已知函数f （x ）=Acos （ωx+φ）的图象如图所示，f （）=﹣，则f （0）=（ ）A ．﹣B ． ﹣C ．D ．8、（遂川中学2015届高三上学期第一次月考）已知24sin 225α=-，(,0)4πα∈-，则sin cos αα+=（ ）A.－15B.15C.－75D.759、（吉安一中2014届高三下学期第一次模拟）已知函数()sin cos f x a x b x =-（a 、b 为常数，0,a x R ≠∈）在4x π=处取得最小值，则函数3()4y f x π=-是（ ） A. 奇函数且它的图象关于点3(,0)2π对称 B. 奇函数且它的图象关于点(,0)π对称 C. 偶函数且它的图象关于点(,0)π对称 D. 偶函数且它的图象关于点3(,0)2π对称 10、（南昌三中2014届高三第七次考试）已知函数)2,2(tan ππω-=在x y 内是减函数，则（ ） A ．0<ω≤1 B ．－1≤ω<0C ．ω≥1D ．ω≤－1二、解答题1、（2014年江西高考）已知函数()sin()cos(2)f x x a x θθ=+++，其中,(,)22a R ππθ∈∈-（1）当4a πθ==时，求()f x 在区间[0,]π上的最大值与最小值；(2)若()0,()12f f ππ==，求,a θ的值.2、（2013年江西高考）在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，已知cosC+（conA-sinA ）cosB=0.（1） 求角B 的大小；若a+c=1，求b 的取值范围3、（2012年江西高考）在△ABC 中，角A,B,C 的对边分别为a ，b ，c 。

课时跟踪检测(二十一) 函数y ＝A sin(ωx ＋φ)的图像及三角函数模型的简单应用(分Ⅰ、Ⅱ卷，共2页) 第Ⅰ卷：夯基保分卷1．(2014·滨州一模)把函数y ＝sin x 的图像上所有点的横坐标缩小到原来的一半，纵坐标保持不变，再把所得函数图像向左平移π4个单位，得到的函数图像的解析式是( )A ．y ＝cos 2xB ．y ＝－sin 2xC ．y ＝sin ⎝⎛⎭⎫2x －π4 D ．y ＝sin ⎝⎛⎭⎫2x ＋π4 2．(2013·全国大纲卷)若函数y ＝sin(ωx ＋φ)(ω>0)的部分图像如图，则ω＝( )A ．5B ．4C ．3D ．23．(2014·威海高三期末)函数f (x )＝sin(2x ＋φ)⎝⎛⎭⎫|φ|<π2的图像向左平移π6个单位后所得函数图像的解析式是奇函数，则函数f (x )在⎣⎡⎦⎤0，π2上的最小值为( ) A ．－32B ．－12C.12D.324．(2013·福建高考)将函数f (x )＝sin (2x ＋θ) ⎝⎛⎭⎫－π2<θ<π2的图像向右平移φ(φ>0)个单位长度后得到函数g (x )的图像，若f (x )，g (x )的图像都经过点P ⎝⎛⎭⎫0，32，则φ的值可以是( ) A.5π3 B.5π6C.π2D.π65.函数f (x )＝A sin(ωx ＋φ)(A ，ω，φ为常数，A ＞0，ω＞0)的部分图像如图所示，则f (0)的值是________．6．某城市一年中12个月的平均气温与月份的关系可近似地用三角函数y ＝a ＋A cos ⎝⎛⎭⎫π6(x －6) (x ＝1,2,3，…，12)来表示，已知6月份的月平均气温最高，为28℃，12月份的月平均气温最低，为18℃，则10月份的平均气温值为________℃.7．已知函数f (x )＝2sin ⎝⎛⎭⎫2x －π4＋1. (1)求它的振幅、最小正周期、初相； (2)画出函数y ＝f (x )在⎣⎡⎦⎤－π2，π2上的图像．8．已知函数f (x )＝23sin ⎝⎛⎭⎫x 2＋π4cos ⎝⎛⎭⎫x 2＋π4－sin(x ＋π)． (1)求f (x )的最小正周期；(2)若将f (x )的图像向右平移π6个单位，得到函数g (x )的图像，求函数g (x )在区间[0，π]上的最大值和最小值．第Ⅱ卷：提能增分卷1．(2014·长春调研)函数f (x )＝A sin(ωx ＋φ)A >0，ω>0，－π2<φ<π2，x ∈R 的部分图像如图所示．(1)求函数y ＝f (x )的解析式；(2)当x ∈⎣⎡⎦⎤－π，－π6时，求f (x )的取值范围．2．已知f (x )＝A sin(ωx ＋φ)(A >0，ω>0)的最小正周期为2，且当x ＝13时，f (x )的最大值为2.(1)求f (x )的解析式．(2)在闭区间⎣⎡⎦⎤214，234上是否存在f (x )的对称轴？如果存在求出其对称轴．若不正在，请说明理由．3．为迎接夏季旅游旺季的到来，少林寺单独设置了一个专门安排游客住宿的客栈，寺庙的工作人员发现为游客准备的一些食物有些月份剩余不少，浪费很严重，为了控制经营成本，减少浪费，就想适时调整投入．为此他们统计每个月入住的游客人数，发现每年各个月份来客栈入住的游客人数会发生周期性的变化，并且有以下规律：①每年相同的月份，入住客栈的游客人数基本相同；②入住客栈的游客人数在2月份最少，在8月份最多，相差约400人； ③2月份入住客栈的游客约为100人，随后逐月递增直到8月份达到最多． (1)试用一个正弦型三角函数描述一年中入住客栈的游客人数与月份之间的关系； (2)请问哪几个月份要准备400份以上的食物？答 案第Ⅰ卷：夯基保分卷1．选A 由y ＝sin x 图像上所有点的横坐标缩小到原来的一半，纵坐标保持不变，所得图像的解析式为y ＝sin 2x ，再向左平移π4个单位得y ＝sin 2⎝⎛⎭⎫x ＋π4，即y ＝cos 2x . 2．选B 由函数的图像可得T 2＝12·2πω＝⎝⎛⎭⎫x 0＋π4－x 0＝π4，解得ω＝4. 3．选A 由函数f (x )的图像向左平移π6个单位得f (x )＝sin ⎝⎛⎭⎫2x ＋φ＋π3的图像，因为是奇函数，所以φ＋π3＝k π，k ∈Z ，又因为|φ|<π2，所以φ＝－π3，所以f (x )＝sin ⎝⎛⎭⎫2x －π3. 又x ∈⎣⎡⎦⎤0，π20，π2，所以2x －π3∈⎣⎡⎦⎤－π3，23π， 所以当x ＝0时，f (x )取得最小值为－32. 4．选B 因为函数f (x )的图像过点P ，所以θ＝π3，所以f (x )＝sin ⎝⎛⎭⎫2x ＋π3；又函数f (x )的图像向右平移φ个单位长度后，得到函数g (x )＝sin ⎣⎡⎦⎤2(x －φ)＋π3， 所以sin ⎝⎛⎭⎫π3－2φ＝32，所以φ可以为5π6. 5．解析：由图可知：A ＝2，T 4＝7π12－π3＝π4，所以T ＝π，ω＝2πT ＝2，又函数图像经过点⎝⎛⎭⎫π3，0，所以2×π3＋φ＝π，则φ＝π3，故函数的解析式为f (x )＝2sin ⎝⎛⎭⎫2x ＋π3， 所以f (0)＝2sin π3＝62.答案：626．解析：依题意知，a ＝28＋182＝23，A ＝28－182＝5，∴y ＝23＋5cos ⎣⎡⎦⎤π6(x －6)， 当x ＝10时，y ＝23＋5cos ⎝⎛⎭⎫π6×4＝20.5. 答案：20.57．解：(1)振幅为2，最小正周期T ＝π，初相为－π4.(2)图像如图所示．8．解：(1)因为f (x )＝3sin ⎝⎛⎭⎫x ＋π2＋sin x ＝3cos x ＋sin x ＝2⎝⎛⎭⎫32cos x ＋12sin x ＝2sin ⎝⎛⎭⎫x ＋π3， 所以f (x )的最小正周期为2π.(2)∵将f (x )的图像向右平移π6个单位，得到函数g (x )的图像，∴g (x )＝f ⎝⎛⎭⎫x －π6＝ 2sin ⎣⎡⎦⎤⎝⎛⎭⎫x －π6＋π3＝2sin ⎝⎛⎭⎫x ＋π6. ∵x ∈[0，π]，∴x ＋π6∈⎣⎡⎦⎤π6，7π6， ∴当x ＋π6＝π2，即x ＝π3时，sin ⎝⎛⎭⎫x ＋π6＝1，g (x )取得最大值2. 当x ＋π6＝7π6，即x ＝π时，sin ⎝⎛⎭⎫x ＋π6＝－12，g (x )取得最小值－1. 第Ⅱ卷：提能增分卷1．解：(1)由题中图像得A ＝1，T 4＝2π3－π6＝π2，所以T ＝2π，则ω＝1.将点⎝⎛⎭⎫π6，1代入得sin ⎝⎛⎭⎫π6＋φ＝1，而－π2<φ<π2，所以φ＝π3，因此函数f (x )＝sin ⎝⎛⎭⎫x ＋π3. (2)由于－π≤x ≤－π6，－2π3≤x ＋π3≤π6，所以－1≤sin ⎝⎛⎭⎫x ＋π3≤12，所以f (x )的取值范围是⎣⎡⎦⎤－1，12. 2．解：(1)由T ＝2知2πω＝2得ω＝π.又因为当x ＝13时f (x )max ＝2，知A ＝2.且13π＋φ＝2k π＋π2(k ∈Z )， 故φ＝2k π＋π6(k ∈Z )．∴f (x )＝2sin ⎝⎛⎭⎫πx ＋2k π＋π6 ＝2sin ⎝⎛⎭⎫πx ＋π6， 故f (x )＝2sin ⎝⎛⎭⎫πx ＋π6. (2)存在．令πx ＋π6＝k π＋π2(k ∈Z )，得x ＝k ＋13(k ∈Z )．由214≤k ＋13≤234.得5912≤k ≤6512，又k ∈Z ，知k ＝5. 故在⎣⎡⎦⎤214，234上存在f (x )的对称轴， 其方程为x ＝163.3．解：(1)设该函数为f (x )＝A sin(ωx ＋φ)＋B (A >0，ω>0，0<|φ|<π)，根据条件①，可知这个函数的周期是12；由②可知，f (2)最小，f (8)最大，且f (8)－f (2)＝400，故该函数的振幅为200；由③可知，f (x )在[2,8]上单调递增，且f (2)＝100，所以f (8)＝500.根据上述分析可得，2πω＝12，故ω＝π6，且⎩⎪⎨⎪⎧ －A ＋B ＝100，A ＋B ＝500，解得⎩⎪⎨⎪⎧A ＝200，B ＝300.根据分析可知，当x ＝2时f (x )最小， 当x ＝8时f (x )最大， 故sin ⎝⎛⎭⎫2×π6＋φ＝－1， 且sin ⎝⎛⎭⎫8×π6＋φ＝1. 又因为0<|φ|<π，故φ＝－5π6.所以入住客栈的游客人数与月份之间的关系式为f (x )＝200sin ⎝⎛⎭⎫π6x －5π6＋300. (2)由条件可知，200sin ⎝⎛⎭⎫π6x －5π6＋300≥400，化简，得 sin ⎝⎛⎭⎫π6x －5π6≥12⇒2k π＋π6≤π6x －5π6≤2k π＋5π6，k ∈Z ， 解得12k ＋6≤x ≤12k ＋10，k ∈Z . 因为x ∈N *，且1≤x ≤12，故x＝6,7,8,9,10.即只有6,7,8,9,10五个月份要准备400份以上的食物．。

高三文科数学阶段质量检查试题(第2周) （考试时间：120分钟 满分100分） 拟题人：冯维丽 审题人：杨艳昌 2014.8.8一、选择题(本大题共10小题，每小题5分，共50分．每小题中只有一项符合题目要求)1、下列函数为偶函数的是（ ）A ．sin y x =B ．3y x =C ．x y e = D．y =2、幂函数()f x x α=的图像经过点)21,4(，则1()4f 的值为（ ）A ．4B ．3C ．2D ．13、函数1()ln(1)f x x =++ （ ）A ．[2,0)(0,2]-B ．(1,0)(0,2]-C ．[2,2]-D ．(1,2]-4、已知函数3log ,0()2,0xx x f x x >⎧=⎨≤⎩,则1(())9f f =( ) A.4 B.14 C.4- D.14- 5、函数()2xf x e x =+-的零点所在的一个区间是（ ）A ．(2,1)--B ．(1,0)-C ．(0,1)D ．(1,2)6、函数⎪⎩⎪⎨⎧≥-<=)0(12)0(2x x x y x 的图象大致是（ ）7、设2131og a =，3.02)21(3log ==c b ，，则（ ） A. a<b<c B. a<c<b C. b<c<a D. b<a<c8、利用计算器，列出自变量和函数值的对应值如下表：那么方程的一个根位于下列区间的（ ）.A.（0.6，1.0）B.（1.4，1.8）C.（1.8，2.2）D.（2.6，3.0） 9、已知函数()f x 是(,)-∞+∞上的偶函数，若对于0x ≥，都有(2()f x f x +=），且当[0,2)x ∈时，2()log (1f x x =+），则(2011)(2012)f f -+的值为（ ） A ．2- B ．1- C ．1 D ．210、设0x 是方程3log 3x x =-的根，且0(,1)x k k ∈+，则k =（ ）A ．（0，1）B ．（1，3）C ．（3，4）D ．（4，+∞）二、填空题(本大题共4小题，每小题5分，共20分，把答案填在题中横线上)11、已知函数3,1,(),1,x x f x x x ⎧≤=⎨->⎩若()2f x =，则x = .12、若函数()()2ln 1f x x ax =++是偶函数，则实数a 的值为 ．13、若函数()() y f x x R =∈满足()()2f x f x +=且[]1,1x ∈-时，()21f x x =-；函数()lg g x x = ，则函数()()()h x f x g x =-在区间[]5,5-内的零点的个数为＿＿＿＿14、已知()f x 为偶函数，且(1)(3),20,()3x f x f x x f x +=--≤≤=当时,则=)2011(f三、解答题(本大题共4小题，共50分，解答应写出文字说明、证明过程或演算步骤)15、（10分）计算： （1）0021)51(1212)4(2---+-+-（2）91log 161log 25log 532∙∙16、（13分）已知定义域为R 的函数ab x f x x+-=22)(是奇函数。

安徽省2015届高三数学（理）一轮复习参考试题：复数一 选择题【2014安徽（理）真题1】设i 是虚数单位，z 表示复数z 的共轭复数． 若,1i z +=则zi z i+⋅= （ ） A ．2- B ． i 2- C ． 2 D ． i 2 【答案】．C【2013安徽（理）真题1】设i 是虚数单位，_z 是复数z 的共轭复数，若|()>0I x f x =+2=2z zi ，则z =（ ）A ．1+iB ．1i -C ．1+i -D ．1-i - 【答案】．A【2012安徽（理）真题1】复数z 满足：()(2)5z i i --=；则z = （ ）()A 22i -- ()B 22i -+()C i 2-2 ()D i 2+2【答案】．D【2011安徽（理）真题1】设i 是虚数单位，复数aii 1+2-为纯虚数，则实数a 为 A ．2 (B) -2 (C) 1-2 (D) 12【答案】．A错误！未指定书签。

．（安徽省迎河中学2014届高三上学期第一次月考数学(理)试题）设复数z 满足(1-i)z=2 i,则z= （ ） A ．1-i B ．-1-i C ．1+i D ．-1+i 【答案】D错误！未指定书签。

．（安徽省望江四中2014届高三上学期第一次月考数学理试题）在复平面内,复数ii+-221对应的点的坐标为 （ ）A ．()1,0-B ．()1,0C ．⎪⎭⎫⎝⎛-53,54 D ．⎪⎭⎫⎝⎛53,54 【答案】A 原式=(12)(2)(2)(2)i i i i --+-=i -,所以,对应的坐标为(0,-1),选A>错误！未指定书签。

．（安徽省望江二中2014届高三复习班上学期第一次月考数学（理）试题）复数满足(1)2z i i +=,则复数Z 的实部与虚部之差为（ ）A ．2-B ．2C ．1D ．0【答案】D错误！未指定书签。

．（安徽省江南十校2014届新高三摸底联考数学理试题）若得利数z满足 (1+3)z=23i(i 为虚数单位),则z 的虚部是（ ） A ．32B ．-32C ．32i D ．-32i 【答案】A错误！未指定书签。