种群数量增长曲线

生物s型曲线
S型曲线（S-Curve）是生物学和生态学中常见的一种增长曲线，通常用于描述种
群数量随时间的变化。

在自然界中，由于资源、空间和其他因素的限制，种群不可能
按照“J”型曲线无限增长。

当种群在一个有限的环境中增长时，随着种群密度的上升，个体间由于有限的空间、食物和其他生活条件而引起的种内斗争必将加剧，以该种群
生物为食的捕食者的数量也会增加，这就会使这个种群的出生率降低，死亡率增高，
从而使种群数量的增长率下降。

当种群数量达到环境条件所允许的最大值时，种群数
量将停止增长，有时会在K值保持相对稳定。

在生物学和生态学研究中，S型曲线被广泛应用于描述种群数量的变化规律。

例如，在疾病传播模型中，S型曲线可以用来描述疾病的传播过程，随着时间的推移，
感染者的数量会逐渐增加，但当感染者数量达到一定水平后，由于免疫力的增强和防
控措施的实施，感染者的数量会逐渐减少。

此外，S型曲线还可以用于描述其他生物学现象，如种群竞争、资源利用等。

在
生态学中，S型曲线可以帮助我们了解物种的生存能力和适应性，以及物种之间的相
互作用和生态平衡。

S型曲线是一种重要的生物学和生态学模型，可以帮助我们更好地理解和描述生
物种群的变化规律。

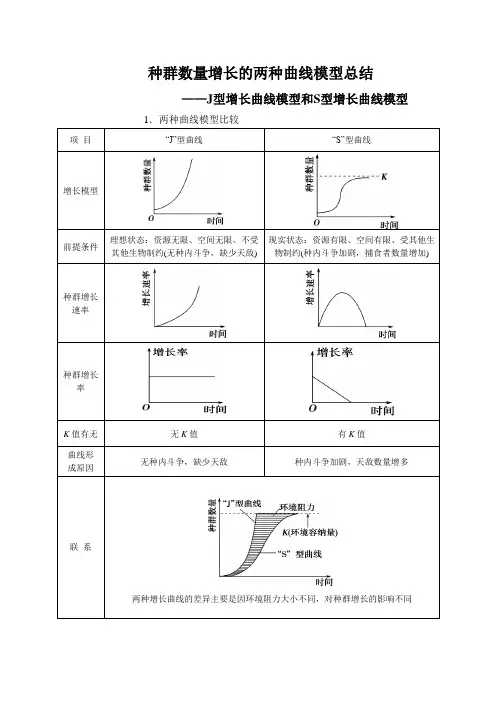
种群数量增长的两种曲线模型总结——J型增长曲线模型和S型增长曲线模型1．两种曲线模型比较两种增长曲线的差异主要是因环境阻力大小不同，对种群增长的影响不同2.K值与K2在实践中的应用例1：右图中种群在理想环境中呈“J”型曲线增长(如图中甲)；在有环境阻力的条件下呈“S”型曲线增长(如图中乙)。

下列有关种群增长曲线的叙述，正确的是()A、环境阻力对种群增长的影响出现在d点之后B、若此图表示蝗虫种群增长曲线，防治害虫应从c点开始C、一个物种引入新的地区后，开始一定呈“J”型增长D、若此图表示草履虫增长曲线，当种群数量达到e点后，增长率为0解析：环境阻力出现在“J”型曲线与“S”型曲线的分叉点（c点）。

c点种群的增长速度最快，所以不能在该点对害虫进行防治；b点蝗虫的数量开始增加，但增长速率还很低，应该从该点开始对害虫进行防治。

一个物种引入新的地区后，有可能不适应当地的环境，所以不一定呈“J”型增长。

【答案】D例2：某研究所调查发现：某种鱼迁入一生态系统后，其种群数量增长率随时间变化的曲线如图所示，请分析回答：t o t1t2 时间（1）在t0-t2时间内，种群数量增长曲线呈；若在t 2时种群的数量为N，则t1在时种群的数量为，t1时该种群年龄组成可能是。

（2）捕获该鱼的最佳时期为时，原因是。

（3）该鱼在t2时期后，种群数量，主要原因是答案（1）S型曲线N／2 增长型（2）T1 在T1时种群增长率最大，捕获该鱼获得的量最大且不影响该鱼类资源的再生（3）不增加种内斗争加剧捕食者数量增加解析:分析图中曲线可知：T0～T2时间内种群数量增长率由小变大，达到最大值后又逐渐变小，因而该种群数量增长呈S型曲线。

在T2时种群数量增长率为0，此时，种群的数量为N，即为最大值，而在T1.时种群数量增长率最大，则这时种群的数量为N／2，种群年龄组成为增长型。

当种群数量增长率最大时捕获该鱼获得的量最大且不影响该鱼类资源的再生，因而此时（T1）为捕获的最佳时期。

第2节种群数量的变化知识点一构建种群增长模型的方法1.数学模型概念,数学模型是用来描述一个系统或它的性质的数学形式，是为了某种目的用字母、数字及其他数学符号建立起来的方程式以及图表、图像等数学表达式。

2.意义,数学模型是联系实际问题与数学规律的桥梁，具有解释、判断、预测等重要作用。

知识点二种群数量的增长,1.种群的“J”型增长(1)“J”型曲线：自然界确有类似细菌在理想条件下种群数量增长的形式，如果以时间为横坐标，种群数量为纵坐标画出曲线来表示，曲线则大致呈“J”型。

(2)“J”型增长的原因：食物充足、没有天敌、气候适宜等，这一理想条件只有在实验室或某物种最初进入一条件非常适宜的环境时才会出现。

(3)“J”型增长的数学模型,模型假设：在食物和空间条件充裕、气候适宜、没有敌害等条件下，种群的数量以一定的倍数增长，第二年是第一年的λ倍。

增长速率不随种群密度的变化而变化。

,建立模型：,一年后该种群的数量应为：N1＝N0λ,两年后该种群的数量应为：N2＝N1×λ＝N0λ2,t年后该种群的数量应为：N t＝N0λt,N0：该种群的起始数量；t：时间；N t：t年后种群数量；λ：增长的倍数。

注：当时，种群数量上升；当λ＝1时，种群数量不变；当时，种群数量下降。

2.种群增长的“S”型曲线,(1)“S”型曲线出现的原因,自然资源是有限的，当种群密度增大时，使生存斗争加剧，种群的增长速率下降。

(2)实例：高斯的实验。

(3)“S”型曲线：种群经过一定时间的增长后，数量趋于稳定的增长曲线，呈“S”型。

①K值：在环境条件不受破坏的情况下，一定空间中所能维持的种群最大数量称为环境容纳量。

a.不同物种在同一环境中K值不同。

b.当环境改变时生物的K值改变。

②K/2值：K值的一半，是种群数量增长最快点。

③增长速率：可以看出种群的增长速率在K/2时最大，K/2之前不断增加，在K/2之后逐渐减小，当达到K值时增长速率为0。

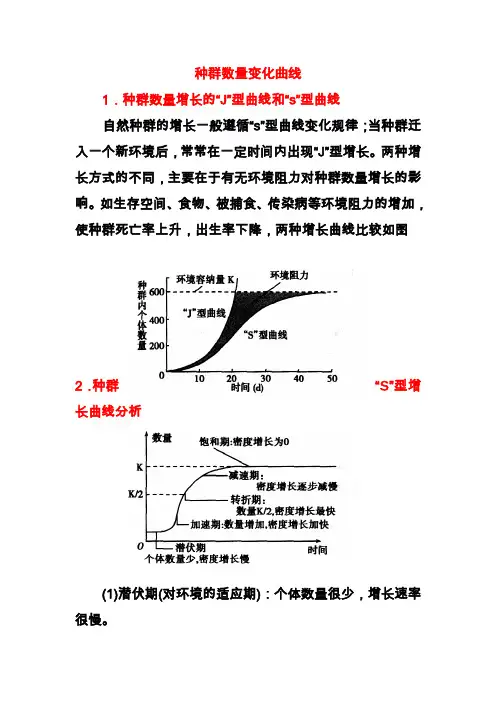
种群数量变化曲线
1．种群数量增长的“J”型曲线和“s”型曲线自然种群的增长一般遵循“s”型曲线变化规律；当种群迁入一个新环境后，常常在一定时间内出现“J”型增长。

两种增长方式的不同，主要在于有无环境阻力对种群数量增长的影响。

如生存空间、食物、被捕食、传染病等环境阻力的增加，使种群死亡率上升，出生率下降，两种增长曲线比较如图
2．种群“S”型增长曲线分析
(1)潜伏期(对环境的适应期)：个体数量很少，增长速率很慢。

(2)快速增长期(对数期)：个体数量快速增加，K／2时，增长率达到最高。

(3)稳定期(饱和期)：随着种群密度增加，个体因食物、空间和其他生活条件的斗争而加剧，同时天敌数量也增长。

种群实际增长率下降。

当数量达到环境条件允许的最大值(K)时，种群停止生长。

种群增长率为零，即出生率：死亡率，但种群数量达到最大。

到达K值后，仍是呈锯齿状波动。

应用：生产上的捕获期就确定在种群数量为K／2时最好。

但杀虫效果最好的时期在潜伏期。

3．种群数量变化曲线与种群增长率曲线的关系
(1)图乙的0f段相当于图甲的ac段。

(2)图乙的f点相当于图甲的c点。

(3)图乙的fg段相当于图甲的cd段。

(4)图乙的g点相当于图甲的de段。

高中生物选择性必修二 生物与环境 第一章 种群及其动态第2、3节 种群数量的变化及影响因素知识点总结一、构建种群增长模型的方法： 1、数学模型：用来描述一个系统或它的性质的数学形式。

2、构建步骤： ①观察研究对象，提出问题。

②提出合理的假设。

③根据实验数据，用适当的数学形式对事物的性质进行表达。

④通过进一步实验或观察等，对模型进行检验或修正。

3、表达形式：二、种群的“J”形增长：1、含义：自然界有类似细菌在理想条件下种群数量增长的形式，如果以时间为横坐标，种群数量为纵坐标画出曲线来表示，曲线则大致呈“J ”型。

2、模型假设（适用条件）：在食物和空间条件充裕、气候适宜、没有天敌和其他竞争物种等条件下。

●或以下情况之一：物种入侵早期阶段、没有环境阻力、理想条件下。

3、数学模型：N t ＝N 0λt其中： N 0为该种群的起始数量t 为时间N t 表示t 年后该种群的数量λ表示该年种群数量是上一年种群数量的倍数4、增长率：（1）定义：该年种群数量比上一年种群数量多了多少倍。

必修1相关知识链接： 模型1、模型定义：是人们为了某种特定的目的而对认识对象所作的一种简化的概括性的描述。

2、模型形式：物理模型、概念模型、数学模型。

3、物理模型：以实物或图画形式直观地表达认识对象的特征。

●注意：拍摄的实物照片与视频不是模型。

4、概念模型：是指以文字表达来抽象概括出事物本身特征的模型。

（2）增长率与λ的关系：增长率=λ-1。

①λ>1，增长率>0，种群数量上升，该种群年龄结构为增长型。

②λ=1，增长率=0，种群数量不变，该种群年龄结构为稳定型。

③λ<1，增长率<0，种群数量下降，该种群年龄结构为衰退型。

（3）“J”型曲线增长率：由于“J”型曲线的λ是常数，值不变，所以其增长率不变。

5、增长速率（看斜率）：（1）定义：单位时间内增加的个体数。

（2）计算方法：（3）“J”型曲线增长率：持续增加。

生物种类数量增长曲线
生物种类数量增长曲线通常指的是种群数量随时间变化的图形表示。

主要类型有两种：
1. J型增长曲线：在理想条件下（无限空间、充足食物、无疾病、无天敌等），种群数量会以恒定的倍数增长，形似字母J，表现为指数增长，开始时增长较慢，随后增速加快。

2. S型增长曲线：在自然环境下，种群受到资源限制时，数量增长先是迅速上升，到达一定密度后增长速率逐渐下降，最终趋于环境容纳量（K值），形成类似英文字母S的曲线。

在种群数量达到K/2时，增长速率最快。

此曲线反映了现实生态系统的种群动态，体现了种群数量与资源、竞争压力之间的关系。

种群数量增长的S型曲线中增长率和增长速率的区分
在学习种群的数量增长曲线时，很多学生对增长率和增长速率不理解，而在习题中也往往将二者混为一谈，实际上二者是有区别的，现将二者区别总结如下。

1.增长率：增长率是指单位时间种群增长数量，[增长率＝出生率—死亡率＝出生数－死亡数）/（单位时间×单位数量）]。

在“J”型曲线增长的种群中，增长率保持不变；而在“S”型增长曲线中增长率越来越小。

2.增长速率：增长速率是指单位时间内种群数量变化率，[增长速率＝（出生数－死亡数）/单位时间]。

种群增长速率就是曲线上通过每一点的切线斜率，不论是“J”型曲线还是“S”型曲线上的斜率总是变化着的。

在“J”型曲线增长的种群中，增长速率是逐渐增大。

在“S”型曲线增长的种群中，“增长速率”是该曲线上“某点”的切线的斜率，斜率越大，增长速率就越大，且斜率最大时在“ 1/2K”。

之后增长变慢，增长速率是逐渐减小。

在“S”曲线到达K值时，增长速率就为0。

在“J”型增长曲线中，每年的增长率不变；由于“J”型增长曲线的斜率是在不断变化的，逐渐增大，直至无穷，所以其增长速率也就不断增大。

在“S”型增长曲线中，每年的增长率由最初的最大值，在环境阻力（空间压力、食物不足等）的作用下，导致出生率下降、死亡率上升，种群数量到达最大值（K值），其增长率不断下降至0，故在“K”时，其增长率为0；而增长速率会有先升后降的变化过程，呈现钟罩形变化曲线，即在“S”型曲线中，开始时斜率为0，斜率逐渐增大，增长速率也就越大，且斜率在1/2K时最大，即在“ 1/2K”时增长速率最大，过后，斜率下降，在K值时降至为0，故在“K”时，其增长速率为0。

种群的数量增长规律学习目标⑴举例说明种群增长的“J”型曲线，以及形成条件、数量变化规律⑵举例说明种群增长的“S”型曲线，以及形成条件、数量变化规律⑶阐明研究种群数量变动的意义⑷探究培养液中酵母菌种群数量的变化课前导学一、种群数量的增长规律1．数学在生物科学中应用的一种主要形式就是建立，主要包括和两个过程。

2．种群增长的“Ｊ”型曲线“Ｊ”型增长的数学模型是在和条件充裕、和等理想条件下，种群的数量增长，第二年的数量是第一年的λ倍。

ｔ年后种群数量可表示为。

Ｎ０为该种群的起始数量，Ｎｔ表示第t代的数量，λ表示该种群数量是一年前种群数量的λ。

3．种群增长的“Ｓ”型曲线种群在一个的环境中，随着种群密度的上升，不仅将加剧，以该种群生物为食的的数量也会增加。

当种群内个体数量达到环境条件所允许的（）时，种群个体数量将不再增加。

5．研究意义：⑴有利于野生生物资源的合理利用和保护；⑵为人工养殖及种植业中合理控制种群数量、适时捕捞、采伐等提供理论依据。

⑶通过研究种群数量变动规律，为害虫的预测及防治提供科学依据。

二、探究培养液中酵母菌种群大小的动态变化1．提出问题：培养一种酵母菌种群的数量是怎样随时间变化的？2．作出假设：酵母菌种群的数量随时间呈____________型增长变化。

3．实验原理：种群的数量变化有一定的规律。

在理想条件下，种群呈“”型增长，在有限的环境下，种群呈“”型增长。

4．设计实验⑴培养液配制：配制质量分数为5%的葡萄糖溶液（葡萄糖50g，1000 mL水）。

⑵分装：在7支试管中各注入10 mL培养液，加棉塞。

⑶灭菌：用高压蒸汽灭菌锅将培养液和取样、计数时所用的滴管分别灭菌。

贴标签。

⑷接种：接种时要在酒精灯附近，用灭菌干净的1mL刻度吸管每次吸取0.1mL酵母菌母液，分别加入每支试管中。

（注意滴加量不要太多，避免初始菌数过多。

）⑸培养：将7支试管置于 20℃的恒温箱中培养。

⑹抽样检测：每天取样时间大体一致，并要遵守无菌操作规范。

班级：___________ 姓名：___________第一节第2课时种群数量的增长规律【学习目标】1．通过探究培养液中酵母菌种群数量的变化，尝试建构种群增长的数学模型。

2．关注人类活动对种群数量变化的影响。

【学习过程】一、建构种群增长模型的方法数学模型是用来描述______________或______________的数学形式。

建立数学模型的研究方法一般包括__________________、__________________、__________________________和______________________________________四个步骤。

特点提醒：针对具体事例理解数学模型的建立过程，要同时联系实验设计的步骤。

二、种群数量的变化条件______________________________________1．“J”型曲线公式______________________________________特点______________________________________条件_____________________________________2. “S”型曲线：特点_____________________________________课堂合作探究种群增长的两种曲线比较1．相同点：它们都表示种群数量随时间变化而变化的关系且都只研究种群数量变化中的增长问题2．不同点1.图中阴影部分代表那些个体？2.S型曲线增长率怎么变化？在左图画出J型曲线的增长率特别注意：①种群数量变化包括增长、波动、稳定、下降等，而“J”型曲线和“S”型曲线都只研究了种群数量增长的规律。

②“J”型曲线反映的种群增长率是一定的；而“S”型曲线所反映的种群增长率是变化的，不能认为“S”型曲线的开始部分是“J”型曲线。

③两种增长方式的差异，主要在于环境阻力的作用。

巩固练习1．在一个玻璃容器内，装入一定量的适合小球藻生活的营养液，接种少量的小球藻，每隔一段时间测定小球藻的个体数量，绘制成曲线，如图所示。