一元二次方程实根分布第九周第五次作业

二次函数与一元二次方程根的分布讲义及作业二次函数与一元二次方程根的分布1. 二次函数的解析式的三种形式2b b 4ac -b 一般式:y =ax +bx +c (a ≠0) ；对称轴方程是x =-；顶点为(-, ) ；2a 2a 4a2两点式：y =a (x -x 1)(x -x 2) ；对称轴方程是；与x 轴的交点为； y =a (x -k ) 2+h ；对称轴方程是；，求f （x ）的表达式顶点式：例1. 设二次函数f （x ）满足f （x －2）=f （－x －2），且图象在y 轴上的截距为1，在x 轴上截得的线段长为2. 一元二次函数的单调性：当a>0时：在为减函数；当a在区间；C.上是减函数，那么（）；D..；B.例2. 如果二次函数例3 二次函数f （x ）的二次项系数为正，且对任意实数x 恒有f （2+x ）=f （2－x ），若f （1－2x ）（1）f(x)=ax+bx+c（a ≠0）的图像与x 轴交点的横坐标是方程_______________的实根（2）若222x 1x 2为f(x)=0的实根，则f(x)在x 轴上截得的线段长应为|x 1-x2|=_________________________(3)当_________________时，恒有f(x)>0;当____________________时，恒有f(x)例4已知f (x ) 是二次函数，不等式f (x )14. 常见的实根分布情况况分两个负根即两根都小于0 两个正根即两根都大于0 一正根一负根即一个根小于0，一布情大致图象（a >0）得出的结论（a）大致图象得出的结论（不讨论综a 合）结论情况大致图象（a >0）得出的结论(x 10⎪⎪⎪-b⎪2a ⎪⎪f (0)>0⎪⎪∆>0⎪⎪-b 0⎪⎪-b a 0两根都小于k 即x 1⎪⎪∆>0⎪⎪-b 0(x 1>0, x 2>0) 个大于0 (x 1⎪⎪∆>0f (0)⎪⎪-b >0 ⎪2a ⎪⎪f (0)>0⎪⎪∆>0f (0)>0⎪⎪-b 2a >0 ⎪⎪⎪f (0)0a ⋅f (0)⎪⎪-b >0 ⎪2a ⎪⎪a ⋅f (0)>0一个根小于k ，一个大于两根都大于k 即k 即x 1>k , x 2>kx 1kk⎪⎪∆>0⎪⎪-b 2a >k f ⎪(k )⎪⎪f (k )>02大致图象（a）得出的结论⎪∆>0⎪b ⎪0⎪b ⎪⎪∆>0⎪b ⎪>k ⎪-2a ⎪⎪⎪f (k )0⎪b ⎪>k ⎪-2a ⎪⎪⎪a ⋅f (k )>0 f (k )>0综）合结论（不讨论a表三：分布情况大致图象（a >0）得出的结论大致图象（a）3a ⋅f (k )两根有且仅有一根在两根都在(m , n )内种）(m , n )内一根在(m , n )内，另一根在（图象有两种情况，只画了一(p , q )内，m⎪∆>0⎪⎪f (m )>0⎪⎪f (n )>0 ⎪b ⎪m2a ⎪⎪f (m )⋅f (n )⎪f (m )>0⎪⎪f (n )⎪f (m )f (n )f p 0⎪得出的结论⎪∆>0⎪⎪f (m )⎪f (n )2a ⎪⎪f (m )⋅f (n )⎪f (m )⎪⎪f (n )>0⎪⎪f (m )f (n )或⎪⎪f p >0f p f q⎪f (m )f (n )⎪⎪⎪f (p )f (q )综）合结论（不讨论a例5. 对于关于x 的方程x +（2m-1）x+4-2m=0 求满足下列条件的m 的取值范围（1）两个正根（2）有两个负根（3）两个根都小于-1（4）两个根都大于1/2 （5）一个根大于2，一个根小于2 （6）两个根都在（0 ，2）内（7）两个根有且仅有一个在（0 . 2）内（8）一个根在（-2 .0）内，另一个根在（1 . 3）内（9）一个正根，一个负根且正根绝对值较大（10）一个根小于2，一个根大于44——————f (m )⋅f (n )29.4课后作业一1. 函数的图象的对称轴为x ＋2=0，则m ；顶点坐标为递减区间为 .22. 已知函数f(x)=ax+2ax+4(a>0),若x 1A .f(x1)f(x2) D.f(x1) 与f(x2) 的大小不能确定3一元二次方程ax 2+2x +1=0,(a ≠0) 有一个正根和一个负根的充分不必要条件是：（） A．a4已知二次函数>0 C ．a 1f (x ) =ax 2+bx +c ，满足条件f (2+x ) =f (2-x ) ，其图象的顶点为A ，又图象与x 轴交于点B 、C ，其中B点的坐标为(-1,0) ，∆ABC 的面积S =54，试确定这个二次函数的解析式．5⑴关于x 的方程x⑵关于x 的方程x⑶关于x 的方程x⑷关于x 的方程mx2222+2(m +3) x +2m +14=0有两实根，且一个大于1，一个小于1，求m 的取值范围；+2(m +3) x +2m +14=0有两实根在[0, 4)内，求m 的取值范围；+2(m +3) x +2m +14=0有两实根在[1, 3]外，求m 的取值范围；+2(m +3) x +2m +14=0有两实根，且一个大于4，一个小于4，求m 的取值范围．5课后作业参考答案1. －2，（－2，3）；（－∞，－2），（－2，+∞）2.A3.C4.5解：令f(x)= x2y =2(x -2) 2-18或y =-2(x -2) 2-18+2(m +3) x +2m +14，2⑴ ∵ 对应抛物线开口向上，∴ 方程有两实根，且一个大于1，一个小于1，等价于f(1)+2(m +3) ∙1+2m +1421． 4⎪f (0) ≥0⎪2m +14≥0⎪f (4) >0⎪16+8(m +3) +2m +14>0⎪27⎪⎪⇔⇔-⎪⎪2⎪m ≤-5或m ≥1⎪∆=4(m +3) -4(2m +14) ≥0⎪⑶ 由图知，原命题等价于21⎪m4⎪f (3)⎪8⎪⎪m >0⎪m或⎪⑷令g(x)= mx +2(m +3) x +2m +14 ，据题意得⎪g (4) 0⎪⎪2可以解得 -19例1. 解：∵f （x －2）=f （－x －2）∴f （x ）的对称轴为x=－2设f （x ）=a（x +2）+c ∵图象在y 轴上的截距为1∴f （0）=4a+c=1 f （x ）=0即ax +4ax+4a+c=0的两个根为x 1、x 2则|x1－x 2|=又∵x 1+x2=－4，x 1x 2=解得：a=c=－1 ∴2222∴|x1－x 2|=例3解析：由f （2+x ）=f （2－x ）知x =2为对称轴，由于距对称轴较近的点的纵坐标较小，∴|1－2x －2|＜|1+2x －x －2|，∴－2＜x ＜0。

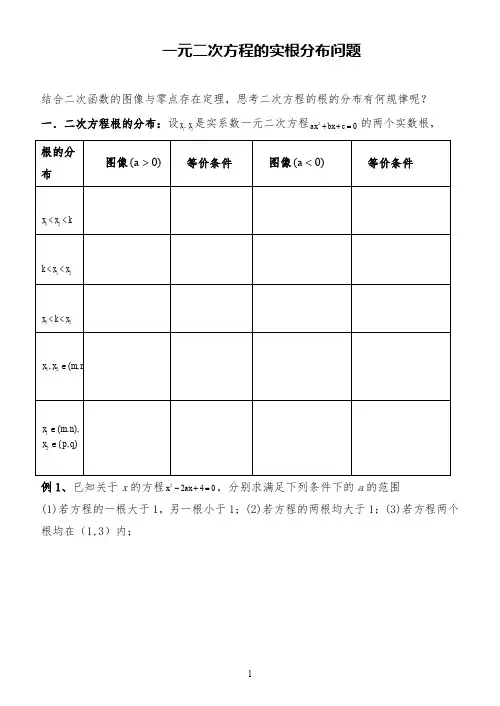
一元二次方程的实根分布问题结合二次函数的图像与零点存在定理，思考二次方程的根的分布有何规律呢？一．二次方程根的分布：设21,x x 是实系数一元二次方程20ax bx c ++=的两个实数根，例1、已知关于x 的方程0422=+-ax x ，分别求满足下列条件下的a 的范围(1)若方程的一根大于1，另一根小于1；(2)若方程的两根均大于1；(3)若方程两个根均在（1,3）内；(4)若方程的一个根在区间（0,1）内，另一个根在区间（2,5）内；思考、二次方程0)(2=++=c bx ax x f 的区间根一般从几个方面考虑？.___________________________例2、已知关于x 的方程03)12(2=-+-x k kx(1)若方程在(—1,1)和(1,3)内各有一个实根，求实数k 的取值范围；(2)若方程有一个根小于1，另一个根大于1，求实数k 的取值范围；(3)若方程在（—1,1）内有两个实数根，求实数k 的取值范围例3、如果函数()m x f x x --=222)(在区间[]1,1-上存在零点，求实数m 的取值范围巩固练习：1若关于x 的一元二次方程07)1(82=-+++m x m x 有两个负数根，求实数m 的取值范围;2若方程0122=+-+m mx x 的两个根一个小于0，另一个大于1，试求m 的取值范围3.已知关于x 的二次方程01222=+++m mx x 的两个的两根，其中一根在区间（－1,0）内，另一根在区间（1,2）内，求实数m 的取值范围4..若关于x 的方程022=+-a x x 的，求a 为何值时（1）方程一根大于1，一根小于1；（2）方程一个根在（—1,1）内，另一个根在（2,3）内；（3）方程的两个根都大于零？。

第二讲：一元二次方程实根分布符号介绍：一般情况下，我们可以把关于x 的函数“y =关于x 的表达式”，记为“()f x =关于x 的表达式”．例如：二次函数22y x x =-可以记为2()2f x x x =-．符号(1)f 表示：当1x =时的函数值．例如：2()2f x x x =-，则2(1)1211f =-⨯=-.1．已知关于x 的方程2220x mx m -++=，(1)有一个根大于1，另一个根小于1，求m 的取值范围．解: 方法一：设原方程的两个根分别是12,x x ， 22(2)4(2)4480m m m m ∆=-+=-->220m m -->，(2)(1)0m m -+>解得：2m >或1m <-． 12122,2x x m x x m +==+121212(1)(1)()10x x x x x x --=-++<2210m m +-+<，解得3m >．综上所述: 3m >．方法二：记()f x =222x mx m -++．(1)0f <，1220m m -++<，解得3m >．总结：若20(0)ax bx c a ++=>的一个根大于r ，另一个根小于r 的等价条件为()0f r <．(2)两个不等实根都大于1，求m 的取值范围．22(2)4(2)4480m m m m ∆=-+=-->220m m -->，(2)(1)0m m -+>解得：2m >或1m <-． (1)0f >，1220m m -++>，解得3m <．对称轴1m >．综上所述：23m <<．总结：若20(0)ax bx c a ++=>的两个不等实根都大于r 的等价条件为0()02f r b r a⎧⎪∆>⎪>⎨⎪⎪->⎩．(3)两个不等实数根都大于1且小于2，求m 的取值范围．22(2)4(2)4480m m m m ∆=-+=-->220m m -->，(2)(1)0m m -+>解得：2m >或1m <-． (1)0f >，解得3m <．(2)0f >，4420m m -++>，解得2m <．对称轴：12m <<．所以，此题无解。

一元二次函数根的分布（20130924）姓名成绩1．设有一元二次方程x2+2(m-1)x+(m+2)＝0．试问：(1)m为何值时，有一正根、一负根．(2)m为何值时，有一根大于1、另一根小于1．(3)m为何值时，有两正根．(4)m为何值时，有两负根．(5)m为何值时，仅有一根在[1，4]内？2. 当m为何值时，方程有两个负数根？3. m取何实数值时，关于x的方程x2+（m-2）x＋5-m=0的两个实根都大于2？4.(1)已知关于x方程：x2-2ax＋a＝0有两个实根α，β，且满足0＜α＜1，β＞2，求实根a的取值范围．(2)m为何实数时，关于x的方程x2+（m-2）x＋5-m=0的一个实根大于2，另一个实根小于2.5．已知函数的图象都在x轴上方，求实数k的取值范围．6．已知关于x的方程（m-1）x2-2mx＋m2+m-6=0有两个实根α，β，且满足0＜α＜1＜β，求实数m 的取值范围．7．已知关于x的方程3x2-5x＋a=0的有两个实根α，β，满足条件α∈（-2，0），β∈（1，3），求实数a的取值范围．8.选择题(1)已知方程(m-1)x2+3x-1=0的两根都是正数，则m的取值范围是（）A．B．C．D．(2)方程x2+(m2-1)x+(m-2)=0的一个根比1大，另一个根比-1小，则m的取值范围是（）A．0＜m＜2 B．-3＜m＜1 C．-2＜m＜0 D．-1＜m＜1(3).已知方程有两个不相等的实数根，则k的取值范围是（）A．B．C．D．9．已知关于x的方程3x2+（m-5）x＋7=0的一个根大于4，而另一个根小于4，求实数m的取值范围．10．已知关于x 的方程x 2＋2mx ＋2m ＋3=0的两个不等实根都在区间（0，2）内，求实数m 的取值范围．11：求下列函数的值域（1）y ＝3x 2＋12x 2 （2）y ＝x ＋1x12：已知54x <，求函数14245y x x =-+-的最大值。

处理一元二次方程实根分布情况下求参问题
的4个方法
一元二次方程是中学数学中的重点难点之一，而处理实根分布情况下的求参问题更是有一定难度。

本文将介绍4种处理实根分布情况下求参问题的方法。

第一种方法是配方法。

这种方法的关键在于化简一元二次方程，使其变成可以用求根公式求解的形式。

如果方程中含有二次项和常数项，但一次项系数为0，那么我们就可以使用配方法将其转化为完全平方的形式。

如果方程中不含常数项，则将其化为ax^2+bx=0的形式。

然后就可以使用求根公式求解。

第二种方法是图像法。

如果一元二次方程表示的是二次函数，那么我们就可以通过观察二次函数的图像得到方程的解。

如果二次函数的顶点在x轴上方，则方程有两个实数根；若顶点在x轴上，则方程有唯一一个实数根；若顶点在x轴下方，则方程没有实数根。

第三种方法是代数法。

对于一元二次方程，我们可以将其写成a(x-p)^2+q=0的形式。

其中p为顶点的x坐标，q为顶点的y坐标。

我们可以根据顶点坐标以及任意点的坐标求出a的值，然后化简得到方程的解。

第四种方法是因式分解法。

有些一元二次方程有明显的因式，可以通过因式分解求解。

例如x^2-4x+3=0，可以分解为(x-1)(x-3)=0，解得x=1或x=3。

以上是处理实根分布情况下求参问题的4种方法。

在实际应用中，我们需要根据具体问题来选择合适的方法。

同时需要注意，一元二次方程有可能没有实数根，这时我们需要使用复数来表示。

二次函数与一元二次方程根的分布【学习目标】1.理解二次函数的概念。

2.熟练掌握二次函数的图像与性质，从而能判断一元二次方程根的存在性及根的个数。

3.体会高中数学中数形结合的思想。

4.以极度的热情投入学习，体会成功的快乐。

【学习重点】基本初等函数的图像及性质。

【学习难点】基本初等函数的图像及性质，基本函数图像的综合运用。

[自主学习]1.二次函数的解读式的三种形式一般式:；对称轴方程是；顶点为；两点式：；对称轴方程是；与轴的交点为；顶点式：；对称轴方程是；顶点为；2.一元二次函数的单调性：当时：为增函数；为减函数；当时：为增函数；为减函数；3.二次函数与一元二次方程，一元二次不等式之间的内在联系<1）f(x>=ax2+bx+c<a≠0）的图像与x轴交点的横坐标是方程_______________的实根b5E2RGbCAP<2）若为f(x>=0的实根，则f(x>在x轴上截得的线段长应为||=__________________________________________________p1Eanq FDPw(3>当_________________时，恒有f(x>>0;当____________________时，恒有f(x><0DXDiTa9E3d4.常见的实根分布情况设为f(x>=0<a>0）的两个实根。

<1）<2）当在区间<m,n）有且只有一个实根时，则有：________________________________________________________________ ___________RTCrpUDGiT(3>当在区间<m,n）有两个实根时，则有：________________________________________________________________ ___________5PCzVD7HxA(4>当在两个区间中各有一个实根时，则有________________________________________________________________ ___________jLBHrnAILg[典型例析]例1.对于关于x的方程x2+<2m-1）x+4-2m=0 求满足下列条件的m的取值范围<1）两个正根 <2）有两个负根<3）两个根都小于-1 <4）两个根都大于1/2<5）一个根大于2，一个根小于2 <6）两个根都在<0 ， 2）内<7）两个根有且仅有一个在<0 . 2）内<8）一个根在<-2 .0）内，另一个根在<1 . 3）内<9）一个正根，一个负根且正根绝对值较大<10）一个根小于2，一个根大于4反思小结：[当堂检测]1. 若关于x的不等式对任意x∈恒成立, 则 m的范围_________________2. 不等式的解集是, 则=____________________3. 已知x 2, 是一次函数且为增函数, 若则.4. 若、是关于x的方程的两个实根, 则的最小值为.5设方程2sin2x-4asinx+1-a=0 在[0, p]上有两个不同的解,实数a的取值范围______________________________xHAQX74J0X6若不等式2sin2x-4asinx+1-a>0 在[0, p]上恒成立, 实数a的取值范围________________________________.LDAYtRyKfE7已知二次函数满足, 其图象顶点为A, 图象与x轴交于点B和C点, 且△ABC的面积为18, 写出此二次函数的解读式. [学后反思]___________________________________________________________Zz z6ZB2Ltk_____________________________________________________________dvz fvkwMI1_____________________________________________________________rqy n14ZNXI申明：所有资料为本人收集整理，仅限个人学习使用，勿做商业用途。

根分布例题选讲例１．设关于x 的方程∈=--+b b x x (0241R ），（1）若方程有实数解，求实数b 的取值范围；（2）当方程有实数解时，讨论方程实根的个数，并求出方程的解。

例２．已知二次函数f (x )=ax 2+bx +c (a ≠0).若方程f (x )=x 无实根，求证：方程f [f (x )]=x 也无实根．例３．设[2,4)A =-，2{40}B x x ax =--≤，若B A ⊆，求实数a 的取值范围．变式：已知方程x 2 + (3m -1)x + (3m -2)=0的两个根都属于( -3, 3)，且其中至少有一个根小于1，求m 的取值范围．例４．已知方程)(0)32()1(242R m m x m x ∈=++-+有两个负根，求m 的取值范围．例５．求实数m 的范围，使关于x 的方程062)1(22=++-+m x m x ．（１）有两个实根，且一个比２大，一个比２小．（２）有两个实根βα,，且满足410<<<<βα．（３）至少有一个正根．例６． 已知关于x 的二次方程x 2+2mx +2m +1=0.(1) 若方程有两根，其中一根在区间(－1，0)内，另一根在区间(1，2)内，求m 的范围.(2) 若方程两根均在区间(0，1)内，求m 的范围.变式：已知方程2x 2 – 2(2a -1)x + a +2=0的两个根在-3与3之间，求a 的取值范围．例７．已知二次方程02)12(2=+--+m x m mx 的两个根都小于1，求m 的取值范围．变式：如果二次函数y =mx 2+(m －3)x +1的图象与x 轴的交点至少有一个在原点的右侧，试求m 的取值范围.例８．已知a 是实数，函数2()223f x ax x a =+--，如果函数()y f x =在区间[]11-，上有零点，求a 的取值范围．二次方程实根分布的一些方法除了直接用于判别二次方程根的情况，在其它的一些场合下也可以适当运用．下面再举两个例子：例９．求函数y = x +1x 2-3x +2(1<x <2)的值域．例10．已知抛物线y = 2x 2-mx +m 与直角坐标平面上两点(0,0), (1,1)为端点的线段（除去两个端点）有公共点，求m 的取值范围．练习题：1．已知二次方程04)32()13(2=+-++-m x m x m 有且只有一个实根属于( -1, 1)，求m 的取值范围．2．已知方程02)12(22=+⋅-+⋅m m m x x 在)1,(-∞上有两个根，求m 的取值范围．3．已知二次方程0)1(2)12(2=-+-+m mx x m 有且只有一个实根属于（1，2），且2,1==x x 都不是方程的根，求m 的取值范围．4．已知二次方程0)1()43()1(2=++++-m x m x m 的两个根都属于（–1，1），求m 的取值范围．5．若关于x 的方程x 2+(a -1)x +1=0有两相异实根，且两根均在区间[0,2]上，求实数a 的取值范围．小测：校园伤害事故的基本法律原则返回本次得分为：6.00/6.00, 本次测试的提交时间为：2018-03-09, 如果你认为本次测试成绩不理想，你可以选择再做一次。

一元二次方程实根分布1、若对所有的实数x ，a ax x ++2恒为正，则（ ）A. a > 0B. a > 4C. a < 0或a > 4D. 0 < a < 42、方程02223=+-x x 的正根的个数是___________个.3、抛物线c bx ax y ++=2的顶点为)11,4(-，且与x 轴的两个交点的横坐标为一正一负，则a ，b ，c 中为正数的（ ）A. 只有aB. 只有bC. 只有cD. 有a 和b4、抛物线14)1(44)(2-++-==k x k x x f y 与x 轴相交于)0,(),0,(21x x 两点，且 21021<<<<x x ，则k 的取值范围是___________________.5、方程)(02)13(722为实数R R R x R x =--++-有两个实根α，β，且0<α<1，1<β<2，则R 的取值范围是_________________________.6、若方程05322=++m x x 的一根大于1，另一根小于1，则m 的取值范围是____________.7、设m 是整数，且方程0232=-+mx x 的两根都大于59-而小于73，则m 等于__________.8、函数2008||20062+-=x x y 的图象与x 轴交点的横坐标之和等于_______________.9、已知抛物线c bx ax y ++=2与直线y = 25 有交点，且仅当3121<<-x 时它在x 轴上方，求a ，b ，c 的取值范围.10、已知m ，n 均为正整数，若关于x 的方程0242=+-n mx x 的两个实数根都大于1且小于2，求m ，n 的值.11、已知抛物线q px x y ++=2上有一点),(00y x M 位于x 轴下方.（1）求证：此抛物线与x 轴交于两点；（2）设此抛物线与x 轴的交点为)0,(1x A ，)0,(2x B ，且21x x <，求证：201x x x <<.12、已知b ，c 为正整数，方程052=++c bx x 的两根都大于1-且小于0，求b ，c 的值.答案：1．D 2. 0 3.a 4.4741<<k 5.12-<<-R 或43<<R 6.1-<m 7.4 8.0 9.24,24,144≥-≤-≤c b a 10.9,6==n m 11.略 12.1,5==c b。

（一元二次方程的有关概念）作业（2）把下列方程化为一般形式，并写出它的二次项系数，一次项系数及常数项①-2x²+2x=x+1 ②(y+2)(y-2)+3y=4（3）一元二次方程a(x+1)²+bx-c=0化为一般形式为4x²+3x+1=0 ,求（2a+b)c的值（4）已知a是方程x²＋x－1=0的一个根，求a²＋a的值（5）已知关于x的一元二次方程（m-3)x²＋2mx＋m²－9=0 的一个根是0，求m的值（用直接开平方法解方程）作业1：用直接开平方法解下列方程（1）x²-4=0 (2) (x-1)²-2=0(3)(2x+3)²-25=0 (4) (x-1)²=(2x+3)²2:在实数范围内定义一种运算★，其规则为a★b=a²-b²,根据这个规则，求方程（x+2)★5=0的解（用因式分解法解方程）作业1：用因式分解法解下列方程（1）-x²=3x (2) 3x(x-2)=2(2-x)(4)2(x-3)²=x²-9 (4) (x-2)²-2(x-2)+1=0(5)(x+1)²-25=0 (6）4x²+x-3=0(7）(x+1）²-6(x+1)+5=02：一个等腰三角形的两条边长分别是方程x²-7x=－10的两个根，求该等腰三角形的周长和面积3：三角形的两条边长分别是3和6，第三边长是方程（配方法解方程）作业1：用配方法解下列方程（1）x²（5）3x²-2x+1=x-22:试用配方法说明，无论x取何值，代数式x²-4x+5 的值总是正数，并指出当x取何值时，这个代数式的值最小，最小值是多少？3：试用配方法说明，无论x取何值，代数式－x²-x-1 的值总是负数，并指出当x取何值时，这个代数式的值最大，最大值是多少？4:试用配方法说明，无论x，y取何值，代数式4x²+y²-4x+6y+11的值总是正数，并指出当x，y取何值时，这个代数式的值最小，最小值是多少？（公式法解方程）作业1：用公式法解下列方程(7)5x²-4x-1=0 (8) 3x²+5(2x+1)=0（一元二次方程解法复习）作业1：运用合适的方法解下列方程（1）x²-6x=-2 (2) x²+3=-5x (3)x3-2x²-3x=0 (4) 3y(2y+1)=4y+2 2:已知2（x²+y²）²-7(x²+y²)+6=0 求x²+y²的值3: 已知3（x²+y²）²+7(x²+y²)-6=0 求x²+y²的值4：已知5（x+y）²+3(x+y)-2=0 求x+y的值6 ：解方程x 4-5x²+4=05：解方程x2-▏x-1▏-1=0(根的判别式)作业1:不解方程，判定下列方程根的情况（1）16x²+8x=-3 (2) 9x²+1=-6x(3） x²+mx-m²=0 (4) x²-7x=182:2k的取值范围．3已知一元二次方程kx2+6x+1=0有实根，求k的取值范围．5：已知关于x的方程kx²-6x+9=0问k为何值时，这个方程（1）有两个不相等的实数根（2）有两个相等的实数根（3）无实数根6：已知关于x的一元二次方程(a+c）x²+2bx+(a-c)=0,其中a,b,c分别是△ABC的三边长，若该方程有两个相等的实数根，试判定△ABC的形状，并说明理由？7：已知关于x的方程mx²-2(m+2)x+m+5=0没有实数根，试判定关于x的方程（m-5)x²-2(m-1)x+m=0的根的情况1：a,b,c为常数，且（a-c)²＞a²+c²试判定关于x的方程ax²+bx+c=0的根的情况2：若关于x的一元二次方程（k-1)x²+4x+1=0有两个不等的实数根，求k的取值范围3：已知一次函数y=kx+b的图象经过一，三，四象限，试判定关于x的方程x²-2x+kb+1=0 根的情况1：已知25x²-(k-1)x+1是一个完全平方式,求k的值2关于x的方程（k-1)x²＋kx＋1=0有实根，求k的取值范围3:已知m为非负整数，且关于x的一元二次方程：（m-2)x²-(2m-3)x+m+2=0有两个实数根，求m的值4:已知关于x的一元二次方程：x²+2x+2k-2=0有两个不相等的实数根，（1）求k的取值范围（2）若k是正整数，求该方程的根5:已知关于x的一元二次方程（m-1）x²-2mx+m+1=0 （1）求出方程的两根（2）m为何整数时，此方程的两根都是正整数6(1)求证：无论k为何值，这个方程总有实数根(2)若等腰三角形ABC的一边长a=4,另两边b,c恰好是这个方程的两根，求△ABC的周长（根与系数的关系）作业2：已知关于x的方程5x²+kx-6=0的一根是2，求k的值及另一个根3: 设a,b是方程x²+2x-2019=0的两个不相等的实数根，代数式a²+3a+b的值4：已知关于x的方程:x²-6x+k=0的两根分别为x1 ,x2(1)若x1=2 ,求x2的值(2)若k=4 ,且x1,x2分别是Rt△ABC的两条直角边的长求Rt△ABC 的面积（利润问题）作业1：某商场销售一批名牌衬衫,现在平均每天能售出20件,每件盈利40元.为了尽快减少库存,商场决定采取降价措施.经调查发现:如果这种衬衫的售价每降低1元时,平均每天能多售出2件.（1）商场要想平均每天盈利1200元,每件衬衫应降价多少元?（2）每件衬衫应降价多少元时，商场平均每天盈利最多，最多是多少？2：某商店以每件16元的价格购进一批商品，物价局限定每件商品的利润不得超过30%．（1）根据物价局规定，此商品每件售价最高可定为多少元？（2）若每件商品售价定为x元，则可卖出（170-5x）件，商店预期要盈利280元，那么每件商品的售价应定为多少元？3：天山旅行社为吸引游客组团去某风景区旅游，推出了如下收费标准：（1）如果人数不超过25人，人均旅游费用为1000元（2）如果人数超过25人，每超1人，人均旅游费用降低20元，但人均旅游费用不低于700元某单位组织员工去某风景区旅游，共支付给旅行社旅游费用27000元，请问该单位这次共有多少名员工去该风景区旅游？1：（2014巴中）某商店准备进一批季节性小家电，单价40元．经市场预测，销售定价为52元时，可售出180个，定价每增加1元，销售量净减少10个；定价每减少1元，销售量净增加10个．因受库存的影响，每批次进货个数不得超过180个，⑴商店若将准备获利2000元，则应进货多少个？定价为多少元？（2）请你为商店估算一下，当定价为多少元时，获得的利润最大？并求最大利润2：某水果批发商场经销一种高档水果,如果每千克盈利10元,每天可售出500千克,经市场调查发现,在进价不变的情况下,若每千克涨价1元,日销售量将减少20千克,现该商场要保证每天盈利6000元,同时又让顾客得到实惠,那么每千克应涨价多少元?3：某市场销售一批名牌衬衫，平均每天可销售20件，每件赢利40元。