(完整版)一元二次方程根的分布练习及答案

微专题12 一元二次方程根的分布问题4种常考题型总结题型1 一元二次方程根在R 上的分布题型2 一元二次方程根的零分布题型3 一元二次方程根的k 分布题型4 一元二次方程根在区间上的分布一、二次函数相关知识对于形如()20=++¹y ax bx c a 的二次函数，有以下性质：1、判别式：ac b 42-=∆；求根公式：aacb b x 242-±-=；2、韦达定理：a b x x -=+21，a cx x =21；3、二次函数对称轴a b x 2-=，定点坐标（a b 2-，acb ac 442-）．二、一元二次方程根的0分布方程的根相对于零的关系。

比如二次方程有一正根，有一负根，其实就是指这个二次方程一个根比零大，一个根比零小，或者说，这两个根分布在零的两侧.0分布结合判别式，韦达定理以及0处的函数值列不等式，即可求出参数的取值范围。

三、一元二次方程根的k 分布分布情况两根都小于k 即k x k x <<21,两根都大于k 即kx k x >>21,一根小于k ，一大于k 即21x k x <<大致图象（a >0）得出的结论()020b k a f k ∆>ìïï-<íï>ïî()020b k a f k ∆>ìïï->íï>ïî()0<k f kkk大致图象（a <0）得出的结论()020b k a f k ∆>ìïï-<íï<ïî()020b k a f k ∆>ìïï->íï<ïî()0>k f 综合结论（不讨论a ）()020b k a a f k ∆>ìïï-<íï×>ïî()020b k a a f k ∆>ìïï->íï×>ïî()0<×k f a 四、一元二次方程根在区间的分布分布情况两根都在()n m,内两根仅有一根在()nm,内（图象有两种情况，只画了一种）一根在()n m ,内，另一根在()q p ,内，qp n m <<<大致图象（0>a ）得出的结论()()0002f m f n b m na ∆>ìï>ïï>íïï<-<ïî()()0<×n f m f ()()()()0000f m f n f p f q ì>ï<ïí<ïï>î或()()()()00f m f n f p f q <ìïí<ïî大致图象（0<a ）得出的结论()()2f mf nbm na∆>ìï<ïï<íïï<-<ïî()()0<×nfmf()()()()f mf nf pf qì<ï>ïí>ïï<î或()()()()f m f nf p f q<ìïí<ïî综合结论（不讨论a）——————()()0<×nfmf()()()()ïîïíì<<qfpfnfmf五、一元二次方程根的分布应用示例在处理参数范围问题时，有时会需要限制一元二次方程的根位于指定范围，这就是一元二次方程根的分布问题．一、方程f(x)＝0有一根大于k，另一根小于k的条件是f(k)＜0示例1:方程8x2－(m－1)x＋m－7＝0两实根一个大于2，另一个小于2，求实数m的取值范围．【解析】设f(x)＝8x2－(m－1)x＋m－7，符合题意的f(x)如图．方程一根大于2，另一根小于2，等价于f(2)＜0，即8·22－(m－1)·2＋m－7＝27－m＜0.解得m的取值范围是m＞27.注：用于限制一元二次方程根的分布的工具有三个：①判别式Δ；②对称轴；③区间端点函数值的符号，但不一定每次每个工具都用到，同学可以结合图形按需取用．二、方程f(x)＝0的一根小于k1，另一根大于k2且k1＜k2的条件是{f(k1)＜0，f(k2)＜0示例2：方程x2－(m－1)x＋m－7＝0两根x1，x2满足x1<－1，x2>2，求实数m的取值范围．【解析】设f(x)＝x2－(m－1)x＋m－7.符合题意的f(x)图象如图．两根x 1，x 2满足x 1<－1，x 2>2，则{f (－1)＜0，f (2)＜0， 即{(－1)2－(m －1)(－1)＋m －7＜0，22－2(m －1)＋m －7＜0，解得m ∈(－1，72).注：如果求出两根：x 1x 2{x 1<－1，x 2>2显然比本例解法要麻烦得多．三、方程f (x )＝0在区间(k ，＋∞)内有两个实根的条件是{Δ≥0，－b2a ＞k ，f (k )＞0示例3：方程8x 2－(m －1)x ＋m －7＝0的两实根都大于1，求实数m 的取值范围．【解析】方法一　设函数f (x )＝8x 2－(m －1)x ＋m －7，作其草图，如图．若两实根均大于1，需{Δ＝(m －1)2－32(m －7)≥0，f (1)＞0，m －116＞1，即{m ≥25或m ≤9，m ∈R ，m ＞17，解得m ≥25.方法二　设方程两根分别为x 1，x 2，则x 1＋x 2＝m －18，x 1x 2＝m －78，因为两根均大于1，所以x 1－1＞0，x 2－1＞0，故有{Δ＝(m －1)2－32(m －7)≥0，(x 1－1)＋(x 2－1)＞0，(x 1－1)(x 2－1)＞0，即{(m －1)2－32(m －7)≥0，m －18－2＞0，m－78－m －18＋1＞0，解得所以m ≥25.【反思与感悟】在方法一中，如果少了条件Δ≥0，就会有导致范围扩大．同学可以自行考虑如果少了条件2，条件3会怎样．在方法二中，{x 1＞1，x 2＞1 ⇒{x 1＋x 2>2，x 1x 2>1， 但{x 1＋x 2>2，x 1x 2>1 ⇏{x 1>1，x 2>1.例如x 1＝4，x 2＝12.所以{Δ≥0，x 1＋x 2＞2，x 1x 2＞1不是等价条件．四、方程f (x )＝0在区间(k 1，k 2)内有两个实根的条件是{Δ≥0，k 1＜－b2a＜k 2，f (k 1)＞0，f (k 2)＞0示例4：方程8x 2－(m －1)x ＋m －7＝0两实根都在区间(1,3)内，求实数m 的取值范围．【解析】　设f (x )＝8x 2－(m －1)x ＋m －7，符合题意的f (x )图象如图则{Δ≥0，f (1)＞0，f (3)＞0，1＜m －116＜3， 即{m ≥25或m ≤9，m ∈R ，m ＜34，17＜m ＜49，所以25≤m ＜34.注：本例中四个限制条件缺一不可，同学可以思考如果去掉其中一个条件会怎样．如去掉对称轴的限制，则会包含两根均小于1或均大于3的情形．其本质是用零点存在定理限制区间(1，m －116)，(m －116，3)上各有一个零点．题型1 一元二次方程根在R 上的分布【例1】“m>2”是“关于x 的方程2210x mx -+=有两个不等实根”的（）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件【答案】D【解析】因为关于x 的方程2210x mx -+=有两个不等实根，所以280m ∆=-＞，解得m -＜m ＞所以“m>2”是“关于x 的方程2210x mx -+=有两个不等实根” 既不充分也不必要条件.故选：D【变式1】已知命题:p “x $ÎR ，关于x 的一元二次方程20x m -+=有实数根”是真命题，则实数m 的取值范围是 .【答案】3m £【解析】因为x $ÎR ，关于x 的一元二次方程20x m -+=有实数根，所以2(40m ∆=--³，解得3m £，故答案为：3m £【变式2】x 的一元二次方程210x kx k +++=没有实数根，则k 的取值范围是___.【答案】(22-+.【解析】∵关于x 的一元二次方程210x kx k +++=没有实数根∴()2Δ410k k =-+<∴2440k k --<解得：22k -<<+【变式3】若下列两个方程：24430x ax a +-+=，2220x ax a +-=至少有一个方程有实根，则实数a 的取值范围为.【答案】32a £-或0a ³.【解析】24430x ax a +-+=有实根，则()2164430a a ∆=--+³，解得12a ³或32a £-，2220x ax a +-=有实根，则2480a a ∆=+³，解得0a ³或2a £-，故实数a 的取值范围是12a a ì³íî或32a ü£-ýþU {0a a ³或}2a £-32a a ì=£-íî或}0a ³.故答案为：32a £-或0a ³.题型2 一元二次方程根的零分布【例2】关于x 的一元二次方程2(2)20x m x m +--=有两个不相等的正实数根，则m 的取值范围是（ ）A ．(,2)(2,0)-¥--UB ．(,2)-¥C ．(0,2)(2,)È+¥D ．(2,)-+¥【答案】A【解析】因为方程2(2)20x m x m +--=有两个不相等的正实数根，所以()22802020m m m m ì-+>ï-+>íï->î，解得0m <且2m ¹-.故选：A.【变式1】关于x 的一元二次方程280x qx q ++-=有两个正实数根，则q 的取值范围是（ ）A ．8q >B ．4q <-C ．8q >或4q <-D ．8q <-【答案】D【解析】因为一元二次方程280x qx q ++-=有两个正实数根，所以2Δ=4(8)>0>08>0q q q q ----ìïíïî，解得8q <-，故选：D【变式2】若一元二次方程2240ax x --=（a 不等于0）有一个正根和一个负根，则实数a 的取值范围为（ ）A ．0a >B ．2a >C ．1a >D ．1a >-【答案】A【解析】因为一元二次方程2240ax x --=（a 不等于0）有一个正根和一个负根，设两根为12,x x ，则()()212Δ244040a x x a ì=--´´->ïí=-<ïî，解得0a >，故选：A 【变式3】一元二次方程()25400ax x a ++=¹有一个正根和一个负根的一个充要条件是（ ）A ．a<0B ．0a >C ．2a <-D ．1a >【答案】A【解析】因为一元二次方程()25400ax x a ++=¹有一个正根和一负根，设两根为1x 和2x ，所以212Δ544040a x x a ì=-´>ïí=<ïî，解得25160a a ì<ïíï<î，故a<0.故选：A.【变式4】关于x 的方程24260x mx m -++=至少有一个负根的充要条件是（ ）A ．32m ³B ．1m £-C ．32m ³或1m £-D ．3m £-【答案】B【解析】当方程没有根时，2168240m m ∆=--<，即2230m m --<，解得312m -<<；当方程有根，且根12,x x 都不为负根时，可得21212Δ16824040260m m x x m x x m ì=--³ï+=³íï=+³î，解得32m ³，综上可知1m >-，即关于x 的方程24260x mx m -++=没有一个负根时，1m >-，所以24260x mx m -++=至少有一个负根的充要条件是1m £-.故选：B题型3 一元二次方程根的k 分布【例3】已知二次函数()()222433y m x m x m =+-+++与x 轴有两个交点，一个大于1，一个小于1，则m可能为（ ）A ．2-B ．1-C ．0D ．1【答案】B【解析】令()f x =()()222433m x m x m +-+++，则()12243321f m m m m =+--++=+，由题可知，2m ¹-，且()()210m f +<，即()()2210m m ++<，解得12, 2m æöÎ--ç÷èø，故所有选项中满足题意的m 的值是：1-.故选：B.【变式1】已知方程2(2)50x m x m +-+-=有两个不相等的实数根，且两个实数根都大于2，则实数m 的取值范围是（ ）A ．(5,4)(4,)--+¥UB ．(5,)-+¥C ．(5,4)--D ．(4,2)(4,)--+¥U 【答案】C【解析】令()2(2)5mf x m x x =+-+-由题可知：()()()()2Δ02450442222242250520m m m m m m m m m m f >ìì--´->><-ìïï-ïï>Þ<-Þ<-íííïïï+-´+->>-î>îïî或则54m -<<-，即(5,4)m Î--故选：C【变式2】关于x 的方程22190x x aæö+++=ç÷èø有两个不相等的实数根12,x x 且121x x <<，那么a 的取值范围是（ ）A ．22,75æö-ç÷èøB ．2,5æö+¥ç÷èøC ．2,7æö-¥-ç÷èøD ．2,011æö-ç÷èø【答案】D【解析】设()2219f x x x a æö=+++ç÷èø，则()22Δ136021110a f a ìæö=+->ïç÷ïèøíï=+<ïî，解得：2011a -<<，即a 的取值范围为2,011æö-ç÷èø.故选：D.【变式3】已知方程240x x a -+=的两根都大于1，则a 的取值范围是（ ）A ．34a <£B ．14a <£C ．1a >D ．4a £【答案】A【解析】设方程240x x a -+=的两根为12,x x ，依题意有：121216404a x x x x a ∆=-³ìï+=íï=î，因12,x x 都大于1，则122x x +>，且12()1(1)0x x ->-，显然122x x +>成立，由12()1(1)0x x ->-得1212()10x x x x -++>，则有410a -+>，解得3a >，由1640a ∆=-³解得：4a £，于是得34a <£，所以a 的取值范围是34a <£.故选：A【变式4】已知关于x 的方程 ()221260x m x m +-++=，当方程的根满足下列条件时，求m 的取值范围.(1)有两个实数根，且一个比2大，一个比2小；(2)至少有一个正根.【答案】(1)1m <-；(2)1m £-【解析】（1）设2()2(1)26f x x m x m =+-++，则由题意可得(2)660f m =+<，解得1m <-.（2）关于x 的方程22(1)260x m x m +-++=无实数根时，()()2414260m m --+<，解得15m -<<，关于x 的方程22(1)260x m x m +-++=有两个负实数根时，()()()2414260210260m m m m ì--+³ï--<íï+>î，解得5m ³，所以关于x 的方程22(1)260x m x m +-++=无实数根时或有两个负实数根时1m >-，可得关于x 的方程22(1)260x m x m +-++=至少有一个正实数根，则1m £-.【变式5】已知a 、b 、R c Î，关于x 不等式22ax bx c x ++<的解集为()1,3．(1)若方程20ax bx c ++=一根小于1-，另一根大于1-，求a 的取值范围；(2)在（1）条件在证明以下三个方程：24430x ax a +-+=，()2210x a x a +-+=，2220x ax a +-=中至少有一个方程有实数解．【答案】(1)1(0,)4；(2)证明见解析【解析】（1）因为关于x 不等式22ax bx c x ++<的解集为()1,3， 即2(2)0ax b x c +-+<的解集为()1,3，故0a >，且1，3为2(2)0ax b x c +-+=的两根，则213,13b ca a-+=-´=，即42,3b a c a =-+=，又方程20ax bx c ++=一根小于1-，另一根大于1-，设2()f x ax bx c =++，而0a >，则(1)0f a b c -=-+<，即14230,4a a a a +-+<\<，结合0a >，可得a 的取值范围为1(0,)4.（2）证明：假设24430x ax a +-+=，()2210x a x a +-+=，2220x ax a +-=都没有实数解，则它们的判别式都小于0，即()2222164(43)0140480a a a a a a ì--+<ïï--<íï+<ïî，即312211320a a a a ì-<<ïïï><-íï-<<ïïî或，解得312a -<<-，这与a 的取值范围为1(0,)4矛盾，故24430x ax a +-+=，()2210x a x a +-+=，2220x ax a +-=中至少有一个方程有实数解．题型4 一元二次方程根在区间上的分布【例4】已知关于x 的方程20x x m ++=在区间()1,2内有实根，则实数m 的取值范围是（ ）A ．[6,2]--B ．(6,2)--C ．(,6][2,)-¥-È-+¥D ．(,6)(2,)-¥--+¥U 【答案】B【解析】因为关于x 的方程20x x m ++=在区间()1,2内有实根，所以2m x x =--在区间()1,2内有实根，令()2f x x x =--，()1,2x Î，所以()f x 在()1,2上单调递减，所以()()()21f f x f <<，即()()6,2f x Î--，依题意y m =与()y f x =在()1,2内有交点，所以()6,2m Î--.故选：B【变式1】关于x 的方程()22210x m x m +-+-=恰有一根在区间()0,1内，则实数m 的取值范围是（ ）A ．13,22éùêúëûB ．12,23æùçúèûC ．1,22éö÷êëøD．{12,623æùÈ-çúèû【答案】D【解析】方程2(2)210x m x m +-+-=对应的二次函数设为：()2(2)21f x x m x m =+-+-因为方程2(2)210x m x m +-+-=恰有一根属于(0,1)，则需要满足：①()()010f f ×<，()()21320m m --<，解得：1223m <<；②函数()f x 刚好经过点()0,0或者()1,0，另一个零点属于(0,1)，把点()0,0代入()2(2)21f x x m x m =+-+-，解得：1=2m ，此时方程为2302x x -=，两根为0，32，而()30,12Ï，不合题意，舍去把点()1,0代入()2(2)21f x x m x m =+-+-，解得：23m =，此时方程为23410x x -+=，两根为1，13，而()10,13Î，故符合题意；③函数与x 轴只有一个交点，()22840m m ∆=--+=，解得6m =±经检验，当6m =- (0,1) 内;综上：实数m的取值范围为{12,623æùÈ-çúèû故选：D【变式2】已知一元二次方程210x mx -+=的两根都在(0,2)内，则实数m 的取值范围是（ ）A ．52,2æöç÷èøB ．52,2éö÷êëøC ．(]5,22,2¥éö--È÷êëøD ．(]5,22,2¥æö--Èç÷èø【答案】B【解析】设()21f x x mx =-+，由题意可得()()2Δ400220102250m m f f m ì=-³ïï<<ïíï=>ï=-+>ïî，解得522m £<.因此，实数m 的取值范围是52,2éö÷êëø.故选：B.【变式3】若关于x 的方程2220x ax a -++=在区间()2,1-上有两个不相等的实数解，则a 的取值范围是（ ）A ．6,15æ--öç÷èøB ．6,15æö-ç÷èøC ．()6,1,5æö-¥--+¥ç÷èøU D ．()6,1,5æö-¥-+¥ç÷èøU 【答案】A【解析】令()222g x x ax a =-++，因为方程2220x ax a -++=在区间()2,1-上有两个不相等的实数解，所以()()Δ0212010a g g >ìï-<<ïí->ïï>î，即()2Δ44202144201220a a a a a a a ì=-+>ï-<<ïí+++>ïï-++>î，解得615a -<<-，所以a 的取值范围是6,15æ--öç÷èø．故选：A ．【变式4】已知关于x 的方程()22140x m x m -++=的两根分别在区间()01，，()12，内，则实数m 的取值范围为 ．【答案】104æöç÷èø，【解析】令()()2214f x x m x m =-++，根据题意得()()()()()22200401011402042140f m f m m f m m ìì>>ïï<Þ-++<ííïï>-++>îî①②③，由①得：0m ¹，由②得：104m <<，由③得：x ÎR ，求交集得：104m <<故m 的取值范围为10,4æöç÷èø.故答案为：10,4æöç÷èø【变式5】设m 为实数，若二次函数2y x x m =-+在区间()1¥-，上有两个零点，则m 的取值范围是 .【答案】10,4æöç÷èø【解析】二次函数2y x x m =-+的对称轴为12x =，且开口向上，因为二次函数2y x x m =-+在区间()1¥-，上有两个零点，所以方程20x x m -+=在区间()1¥-，内有两个不同的根，记方程20x x m -+=的两根为12,x x ，则()()()()()1212121212Δ140112120111110m x x x x x x x x x x m ì=->ï-+-=+-=-<íï-×-=-++=-+>î，解得104m <<，所以104m æöÎç÷èø，.故答案为：104æöç÷èø，【变式6】关于x 的方程2(3)0x m x m +-+=满足下列条件，求m 的取值范围．(1)有两个正根；(2)一个根大于1，一个根小于1；(3)一个根在(2,0)-内，另一个根在(0,4)内；(4)一个根小于2，一个根大于4；(5)两个根都在(0,2)内．【答案】(1)01m <£(2)1m <(3)405m -<<(4)45<-m (5)213m <£【分析】根据二次方程根的分布的性质逐一解决每个小问.【详解】（1）令2()(3)f x x m x m =+-+，设()0f x =的两个根为12,x x .由题得()12122300Δ340x x m x x m m m ì+=->ïï=>íï=--³ïî，解得01m <£.（2）若方程2(3)0x m x m +-+=的一个根大于1，一个根小于1，则(1)220f m =-<，解得1m <（3）若方程2(3)0x m x m +-+=一个根在(2,0)-内，另一个根在(0,4)内，则(2)100(0)0(4)540f m f m f m -=->ìï=<íï=+>î，解得405m -<<（4）若方程2(3)0x m x m +-+=的一个根小于2，一个根大于4，则(2)320(4)540f m f m =-<ìí=+<î，解得45<-m （5）若方程2(3)0x m x m +-+=的两个根都在(0,2)内，则()()()22320003022Δ340f m f m m m m ì=->ï=>ïï-í<-<ïï=--³ïî，解得213m <£。

微专题11二次函数根的分布问题【方法技巧与总结】1、实系数一元二次方程20(0)ax bx c a ++=≠的实根符号与系数之间的关系（1）方程有两个不等正根12,x x ⇔212124000b ac b x x a c x x a ⎧⎪∆=->⎪⎪+=->⎨⎪⎪=>⎪⎩（2）方程有两个不等负根12,x x ⇔212124000b ac b x x a c x x a ⎧⎪∆=->⎪⎪+=-<⎨⎪⎪=>⎪⎩（3）方程有一正根和一负根，设两根为12,x x ⇔120cx x a=<2、一元二次方程20(0)ax bx c a ++=≠的根的分布问题一般情况下需要从以下4个方面考虑：（1）开口方向；（2）判别式；（3）对称轴2bx a=-与区间端点的关系；（4）区间端点函数值的正负．设12,x x 为实系数方程20(0)ax bx c a ++=>的两根，则一元二次20(0)ax bx c a ++=>的根的分布与其限定条件如表所示．根的分布图像限定条件12m x x <<02()0b m a f m ∆>⎧⎪⎪->⎨⎪⎪>⎩12x m x <<()0f m <12x x m<<02()0b m a f m ∆>⎧⎪⎪-<⎨⎪⎪>⎩在区间(,)m n 内没有实根∆<12120x x m x x m∆==≤=≥或02()0b m a f m ∆>⎧⎪⎪-<⎨⎪⎪≥⎩02()0b n a f n ∆>⎧⎪⎪->⎨⎪⎪≥⎩()0()0f m f n ≤⎧⎨≤⎩在区间(,)m n 内有且只有一个实根()0()0f m f n >⎧⎨<⎩()0()0f mf n<⎧⎨>⎩在区间(,)m n内有两个不等实根2()0()0bm naf mf n∆>⎧⎪⎪<-<⎪⎨⎪>⎪>⎪⎩【题型归纳目录】题型一：正负根问题题型二：根在区间的分布问题题型三：整数根问题题型四：范围问题【典型例题】题型一：正负根问题例1．（2022·河南·郑州市回民高级中学高一阶段练习）已知m为实数，命题甲：关于x的不等式240mx mx+-<的解集为R；命题乙：关于x的方程22200x mx m-++=有两个不相等的负实数根．若甲、乙至少有一个为真命题，求实数m的取值范围为_______．【答案】(20,0]-【解析】由命题甲：关于x的不等式240mx mx+-<的解集为R，当0m=时，不等式40-<恒成立；当0m≠时，则满足2160mm m<⎧⎨∆=+<⎩，解得160m-<<，综上可得160m-<≤．由命题乙：关于x的方程22200x mx m-++=有两个不相等的负实数根，则满足2121244(20)020200m m x x m x x m ⎧∆=-+>⎪+=<⎨⎪=+>⎩，整理得2200020m m m m ⎧-->⎪<⎨⎪>-⎩，所以45020m m m m <->⎧⎪<⎨⎪>-⎩或，解得204m -<<-．所以甲、乙至少有一个为真命题时，有160m -<≤或204m -<<-，可得200m -<≤，即实数m 的取值范围为(20,0]-．故答案为：(20,0]-．例2．（2022·全国·高一单元测试）关于x 的方程2210ax x ++=的实数根中有且只有一个负实数根的充要条件为____________.【答案】0a ≤或1a =【解析】若方程2210ax x ++=有且仅有一个负实数根，则当0a =时，12x =-，符合题意.当0a ≠时，方程2210ax x ++=有实数根，则440a ∆=-≥，解得1a ≤，当1a =时，方程有且仅有一个负实数根1x =-，当1a <且0a ≠时，若方程有且仅有一个负实数根，则10a<，即0a <.所以当0a ≤或1a =时，关于x 的方程2210ax x ++=的实数根中有且仅有一个负实数根.综上，“关于x 的方程2210ax x ++=的实数根中有且仅有一个负实数根”的充要条件为“0a ≤或1a =”.故答案为：0a ≤或1a =.例3．（2022·甘肃·兰化一中高一阶段练习）若一元二次方程2330kx kx k ++-=的两根都是负数，求k 的取值范围为___________.【答案】125k ≤-或3k >【解析】首先0k ≠，设方程2330kx kx k ++-=的两根为12,x x ，则12121200,00x x x x x x +<⎧<<⇔⎨>⎩，所以2Δ94(3)03030k k k kkk k⎧⎪=--≥⎪⎪-<⎨⎪-⎪>⎪⎩，又0k ≠，解得125k ≤-或3k >．故答案为：125k ≤-或3k >．例4．（2022·全国·高一专题练习）已知关于x 的二次方程2(21)210m x mx m +-+-=有一正数根和一负数根，则实数m 的取值范围是_____．【答案】112m -<<【解析】由题意知，二次方程有一正根和一负根，得2101021m m m +≠⎧⎪-⎨<⎪+⎩，解得112m -<<.故答案为：112m -<<例5．（2022·河南·高一阶段练习）（1）若不等式210ax bx +-<的解集是113x x ⎧⎫-<<⎨⎬⎩⎭∣，求,a b 的值；（2）若31b a =--，且关于x 的方程210+-=ax bx 有两个不同的负根，求a 的取值范围.【解析】（1）由题意可得1-和13是方程210+-=ax bx 的两个实根，则11,31113b a a ⎧-+=-⎪⎪⎨-⎪-⨯=⎪⎩解得3,2a b ==.（2）因为31b a =--，所以()23110ax a x -+-=，由题可知Δ0>，则1a <-或19a >-，由题意，方程有两个负根，即310,10,a a a +⎧<⎪⎪⎨-⎪>⎪⎩解得103-<<a .综上，实数a 的取值范围是109aa ⎧⎫-<<⎨⎬⎩⎭∣.例6．（2022·辽宁·沈阳市第八十三中学高一阶段练习）已知1x ､2x 是一元二次方程24410kx kx k -++=的两个实数根．(1)若1x ､2x 均为正根，求实数k 的取值范围；(2)是否存在实数k ，使得()()12123222x x x x --=-成立？若存在，求出k 的值；若不能存在，请说明理由．【解析】（1）由题意，一元二次方程有两个正根1x ､2x 故20,(4)16(+1)0k k k k ≠∆=-≥，即0k ≤，且121210104x x k x x k +=>⎧⎪+⎨=>⎪⎩，解得：1k <-．（2）由题意，当0∆≥，即0k ≤时，有121211,4k x x x x k++==()()2221212121212129(1)93222+252()92442k k x x x x x x x x x x x x k k ++--=-=+-=-=-=-解得：95k =，与0k ≤矛盾.故不存在实数k ，使得()()12123222x x x x --=-成立题型二：根在区间的分布问题例7．（2022·全国·高一专题练习）已知一元二次方程x 2＋ax ＋1＝0的一个根在(0，1)内，另一个根在(1，2)内，则实数a 的取值范围为________．【答案】5(,2)2--【解析】设f (x )＝x 2＋ax ＋1，由题意知(0)10(1)20(2)520f f a f a =>⎧⎪=+<⎨⎪=+>⎩，解得－52<a <－2.故答案为：5(,2)2--.例8．（2022·全国·高一课时练习）已知关于x 的方程220x x a -+=．(1)当a 为何值时，方程的一个根大于1，另一个根小于1？(2)当a 为何值时，方程的一个根大于1-且小于1，另一个根大于2且小于3？(3)当a 为何值时，方程的两个根都大于0？【解析】（1）二次函数22y x x a =-+的图象是开口向上的抛物线，故方程220x x a -+=的一个根大于1，另一个根小于1，则2120a -+<，解得1a <，所以a 的取值范围是{}1a a <．（2）方程220x x a -+=的一个根大于1-且小于1，另一个根大于2且小于3，作满足题意的二次函数22y x x a =-+的大致图象，由图知，120120440960a a a a ++>⎧⎪-+<⎪⎨-+<⎪⎪-+>⎩，解得30a -<<．所以a 的取值范围是{}30a a -<<．（3）方程220x x a -+=的两个根都大于0，则Δ4400a a =-≥⎧⎨>⎩，解得01a <≤，所以a 的取值范围是{}01a a <≤．例9．（2022·全国·高一专题练习）已知关于x 的一元二次方程2220x ax a -++=，当a 为何值时，该方程：有不同的两根且两根在(1,3)内．【解析】令2()22f x x ax a =-++，因为方程2220x ax a -++=有不同的两根且两根在(1,3)内，所以213Δ44(2)0(1)30(3)1150a a a f a f a <<⎧⎪=-+>⎪⎨=->⎪⎪=->⎩，解得1125<<a ，故答案为：112,5⎛⎫⎪⎝⎭例10．（2022·江苏·高一专题练习）已知二次函数()2221R y x tx t t =-+-∈.(1)若该二次函数有两个互为相反数的零点，解不等式22210x tx t -+-≥；(2)若关于x 的方程22210x tx t -+-=的两个实根均大于2-且小于4，求实数t 的取值范围．【解析】（1）设二次函数()2221y x tx t t =-+-∈R 的两个零点分别为1x ，2x ，由已知得120x x +=，而122x x t +=，所以20t =，故0=t ，不等式22210x tx t -+-≥即210x -≥，解得1≥x 或1x ≤-，故不等式的解集为{1x x ≥或}1≤-x .（2）因为方程22210x tx t -+-=的两个实根均大于2-且小于4，所以()()()()222222Δ2t 4t 102t 422t 2t 1042t 4t 10⎧=---≥⎪⎪-<<⎨⎪--⨯-+->⎪-⨯+->⎩，即2240244308150t t t t t ≥⎧⎪-<<⎪⎨++>⎪⎪-+>⎩，解得：13t -<<，即实数t 的取值范围为{}13t t -<<.例11．（2022·全国·高一单元测试）求实数m 的范围，使关于x 的方程()221 260.x m x m +-++=(1)有两个实根，且一个比2大，一个比2小；(2)有两个实根 αβ，，且满足014αβ<<<<；(3)至少有一个正根.【答案】(1)1m <-(2)7554m -<<-(3)1m ≤-【分析】设()()22126y f x x m x m ==+-++，一元二次方程根的分布主要从对称轴、判别式、端点值、开口方向这几个方面来确定.（1）设()()22126y f x x m x m ==+-++．依题意有()20f <，即()441260m m +-++<，得1m <-．（2）设()()22126y f x x m x m ==+-++．依题意有()()()02601450410140f m f m f m ⎧=+>⎪=+<⎨⎪=+>⎩，解得7554m -<<-．（3）设()()22126y f x x m x m ==+-++．方程至少有一个正根，则有三种可能：①有两个正根，此时可得()()Δ0002102f m ⎧⎪≥⎪⎪>⎨⎪-⎪>⎪-⎩，即153.311m m m m m ≤-≥⎧⎪>-∴-<≤-⎨⎪<⎩或．②有一个正根，一个负根，此时可得()00f <，得3m <-．③有一个正根，另一根为0，此时可得()6203210m m m +=⎧∴=-⎨-<⎩，．综上所述，得1m ≤-．例12．（2022·上海市七宝中学高一阶段练习）方程()2271320x a x a a -++--=的一个根在区间()0,1上，另一个根在区间()1,2上，则实数a 的取值范围为___________.【答案】()()2,13,4--【解析】令()()227132f x x a x a a =-++--，因为程()2271320x a x a a -++--=的一个根在区间()0,1上，另一个根在区间()1,2上，所以()()()001020f f f ⎧>⎪<⎨⎪>⎩，即()22220713202821320a a a a a a a a ⎧-->⎪--+--<⎨⎪-++-->⎩，解得21a -<<-或34a <<，所以实数a 的取值范围为()()2,13,4--.故答案为：()()2,13,4--.例13．（2022·全国·高一专题练习）关于x 的方程()2140x a x --+=在区间[]1,3内有两个不等实根，则实数a 的取值范围是_____．【答案】16(5,]3【解析】关于x 的方程()2140x a x --+=在区间[]1,3内有两个不等实根，令()()214f x x a x =--+，则有()()()2Δ1160113216031630a a f a f a ⎧=-->⎪-⎪<<⎪⎨⎪=-≥⎪=-≥⎪⎩，解得1653a <≤，所以实数a 的取值范围是16(5,]3.故答案为：16(5,]3例14．（2022·全国·高一单元测试）方程()2250x a x a --+-=的两根都大于2，则实数 a 的取值范围是_____．【答案】54a -<≤-【解析】由题意，方程()2250x a x a +=－－－的两根都大于 2，令()()225f x x a x a =+－－－，可得()020222f a⎧⎪≥⎪>⎨⎪-⎪>⎩，即2165024a a a ⎧≥⎪+>⎨⎪->⎩，解得54a <≤－－．故答案为：54a -<≤-.例15．（2022·全国·高一专题练习）已知关于x 的方程220ax x ++=的两个实根一个小于0，另一个大于1，则实数a 的取值范围是_____．【答案】()3,0-【解析】显然0a ≠，关于x 的方程220ax x ++=对应的二次函数()22f x ax x =++当0a >时，二次函数()22f x ax x =++的图象开口向上，因为220ax x ++=的两个实根一个小于0，另一个大于1等价于二次函()22f x ax x =++的图象与x 轴的两个零点一个小于0，另一个大于1，所以()()0010f f ⎧<⎪⎨<⎪⎩，即2030a <⎧⎨+<⎩，解得a ∈∅；②当0a <时，二次函数()22f x ax x =++的图象开口向下，因为220ax x ++=的两个实根一个小于0，另一个大于1等价于二次函()22f x ax x =++的图象与x 轴的两个零点一个小于0，另一个大于1，所以()()0010f f ⎧>⎪⎨>⎪⎩，即2030a >⎧⎨+>⎩，解得30a -<<．；综上所述，实数a 的范围是()3,0-．故答案为：()3,0-．例16．（2022·全国·高一专题练习）已知方程()()22110x a x a a -+++=的两根分别在区间()0,1，()1,3之内，则实数a 的取值范围为______．【答案】()0,1.【解析】方程()()()()2211010x a x a a x a x a ⎡⎤+++=⇒--+=⎣⎦－∴方程两根为12,1x a x a ==+，若要满足题意，则01113a a <<⎧⎨<+<⎩，解得01a <<，故答案为：()0,1.例17．（2022·上海·高一专题练习）方程2240x ax -+=的两根均大于1，则实数a 的取值范围是_______【答案】5[2,)2【解析】2240x ax -+=的两个根都大于121520Δ4160a a a >⎧⎪∴->⎨⎪=-≥⎩，解得522a ≤<可求得实数a 的取值范围为5[2,2故答案为：5[2,)2例18．（2022·湖北·华中师大一附中高一开学考试）关于x 的方程()2290ax a x a +++=有两个不相等的实数根12,x x ，且121x x <<，那么a 的取值范围是（）A ．2275a -<<B ．25a >C ．27a <-D ．2011a -<<【答案】D【解析】当0a =时，()2290ax a x a +++=即为20x =，不符合题意；故0a ≠，()2290ax a x a +++=即为22190x x a ⎛⎫+++= ⎪⎝⎭，令2219y x x a ⎛⎫=+++ ⎪⎝⎭，由于关于x 的方程()2290ax a x a +++=有两个不相等的实数根12,x x ，且121x x <<，则()229y ax a x a =+++与x 轴有两个交点，且分布在1的两侧，故1x =时，0y <，即211190a ⎛⎫++⨯+< ⎪⎝⎭，解得211a<-，故2011a -<<，故选：D例19．（2022·全国·高一课时练习）关于x 的方程()22210x m x m +-+-=恰有一根在区间()0,1内，则实数m 的取值范围是（）A ．13,22⎡⎤⎢⎥⎣⎦B ．12,23⎛⎤ ⎥⎝⎦C ．1,22⎡⎫⎪⎢⎣⎭D．{12,623⎛⎤⋃- ⎥⎝⎦【答案】D【解析】方程2(2)210x m x m +-+-=对应的二次函数设为：()2(2)21f x x m x m =+-+-因为方程2(2)210x m x m +-+-=恰有一根属于(0,1)，则需要满足：①()()010f f ⋅<，()()21320m m --<，解得：1223m <<；②函数()f x 刚好经过点()0,0或者()1,0，另一个零点属于(0,1)，把点()0,0代入()2(2)21f x x m x m =+-+-，解得：12m =，此时方程为2302x x -=，两根为0，32，而()30,12∉，不合题意，舍去把点()1,0代入()2(2)21f x x m x m =+-+-，解得：23m =，此时方程为23410x x -+=，两根为1，13，而()10,13∈，故符合题意；③函数与x 轴只有一个交点，横坐标属于(0,1)，()2(2)4210m m ∆=---=，解得6m =±当6m =+2(2)210x m x m +-+-=的根为2-若6m =-2(2)210x m x m +-+-=2，符合题意综上：实数m的取值范围为{12,623⎛⎤⋃- ⎥⎝⎦故选：D题型三：整数根问题例20．（2022·上海市实验学校高一开学考试）已知12,x x 是一元二次方程24410kx kx k -++=的两个实数根.(1)是否存在实数k ，使得()()12123222x x x x --=-成立？若存在，求出k 的值；若不存在，请说明理由；(2)求使12212x x x x +-的值为整数的实数k 的整数值.【解析】（1）假设存在实数k ，使得()()12123222x x x x --=-成立，一元二次方程24410kx kx k -++=的两个实数根，()2400Δ(4)441160k k k k k k ≠⎧∴⇒<⎨=--⋅+=-⎩，(不要忽略判别式的要求)，由韦达定理得1212114x x k x x k +=⎧⎪+⎨=⎪⎩，()()()()2221212121212129322252942k x x x x x x x x x x x x k +∴--=+-=+-=-=-，95k ⇒=但0k <，∴不存在实数k ，使得()()12123222x x x x --=-成立.（2）()22212121221121244224411x x x x x x k x x x x x x k k +++-==-=-=-++，∴要使其值是整数，只需要1k +能被4整除，故1124k +=±±±，，，即021335k =---，，，，，，0k <，235k ∴=---，，.例21．（2022·上海·高三专题练习）已知,a Z ∈关于x 的一元二次不等式260x x a -+≤的解集中有且仅有3个整数，则所有符合条件的a 的值之和是（）A ．13B ．18C ．21D ．26【答案】C【解析】设2()6f x x x a =-+，其图象为开口向上，对称轴为3x =的抛物线，根据题意可得，3640a ∆=->，解得9a <，因为()0f x ≤解集中有且仅有3个整数，结合二次函数的对称性可得(2)0(1)0f f ≤⎧⎨>⎩，即4120160a a -+≤⎧⎨-+>⎩，解得58a <≤，又,a Z ∈所以a =6，7，8，所以符合题意的a 的值之和6+7+8=21.故选：C例22．（多选题）（2022·全国·高一课时练习）已知a ∈Z ，关于x 的一元二次不等式x 2－6x ＋a ≤0的解集中有且仅有3个整数，则a 的值可以是（）A ．5B ．6C ．7D ．9【答案】BC【解析】设()26f x x x a =-+，函数图象开口向上，且对称轴为3x =，因此关于x 的一元二次不等式x 2－6x ＋a ≤0的解集中有且仅有3个整数时，需满足()()2010f f ⎧≤⎪⎨>⎪⎩，即2226201610a a ⎧-⨯+≤⎨-⨯+>⎩，解得58a <≤，又因为a ∈Z ，所以6a =或7或8，故选：BC.例23．（2022·全国·高一专题练习）若方程()22460x kx x --+=有两个不相等的实根，则k 可取的最大整数值是______.【答案】1【解析】方程化为()221860k x x --+=，由()Δ6424210k =-->，12k ≠解得116k <，所以k 最大整数值是1.故答案为：1.题型四：范围问题例24．（2022·上海·高一专题练习）已知t 是实数，若a ，b 是关于x 的一元二次方程2210x x t -+-=的两个非负实根，则()()2211a b --的最小值是___________.【答案】3-【解析】a ，b 是关于x 的一元二次方程2210x x t -+-=的两个非负实根，∴可得2a b +=，10ab t =-≥，1t ∴≥，又()4410t ∆=--≥，可得2t ≤，12t ∴≤≤，又()()()()()()222222211121a b ab a b ab a b ab --=-++=-+++()()()()2221114211a b t t ∴--=--+-+，24t =-，又12t ≤≤，2340t ∴-≤-≤，故答案为：3-．例25．（2022·吉林省实验中学高一阶段练习）设方程240x mx m -+=的两实根分别为12,x x .(1)当1m =时，求1211+x x 的值；(2)若120,0x x >>，求实数m 的取值范围及124x x +的最小值.【解析】（1）当1m =时，方程为2410x x -+=，2(4)4120∆=--=>，所以12124,1x x x x +=⋅=，122112114x x x x x x ∴+⋅+==.（2）因为240x mx m -+=两根120,0x x >>，所以21212Δ1640400m m x x m x x m ⎧=-≥⎪+=>⎨⎪⋅=>⎩，解得14m ≥.因为12124x x x x +=，120,0x x >>，所以12114x x +=，所以211212121241111194(4)()(5)54444x x x x x x x x x x ⎛⎫+=++=++≥+= ⎪ ⎪⎝⎭，当且仅当21124x x x x =，即1233,48x x ==时等号成立，此时91324m =>符合题意，124x x ∴+的最小值为94.例26．（2022·北京海淀·高一期末）已知函数()22f x x bx c =++（b ，c 为实数），()()1012f f -=.若方程()0f x =有两个正实数根1x ，2x ，则1211+x x 的最小值是（）A ．4B ．2C ．1D ．12【答案】B【解析】因为函数()22f x x bx c =++（b ，c 为实数），()()1012f f -=，所以1012200288b c b c +=++-，解得4b =-，所以()224f x x x c -+=，因为方程()0f x =有两个正实数根1x ，2x ，所以()Δ168000c f c =-≥⎧⎨=>⎩，解得02c <≤，所以121212112422x x c x x x x c =++==≥，当c =2时，等号成立，所以其最小值是2，故选：B例27．（2022·江苏·高一）已知关于x 的方程230x kx k -++=有两个正根，那么两个根的倒数和最小值是（）A ．-2B ．23C ．89D ．1【答案】B【解析】由题意可得∆2()4(3)0k k =--+ ，解得6k 或2k ≤-，设两个为1x ，2x ，由两根为正根可得12120·30x x k x x k +=>⎧⎨=+>⎩，解得0k >，综上知，6k .故两个根的倒数和为12121211x x x x x x ++=1331k k k==++，6k ，∴1106k < ，3102k < ，故33112k <+，∴12331k+，故两个根的倒数和的最小值是23.故选：B例28．（2022·上海·华师大二附中高一期中）已知实数a b <，关于x 的不等式()210x a b x ab -+++<的解集为()12,x x ，则实数a 、b 、1x 、2x 从小到大的排列是()A ．12a x x b <<<B ．12x a b x <<<C ．12a x b x <<<D ．12x a x b<<<【答案】A【解析】由题可得：12x x a b +=+，121x x ab =+.由a b <，12x x <，设1x a m =+，则2x b m =-.所以212()()()1a m b m ab m b a m ab x x =+-=+--=+，所以2()1m b a m --=，21m m b a+=-.又a b <，所以0b a ->，所以0m >.故1x a >，2x b <.又12x x <，故12a x x b <<<.故选：A.例29．（2022·福建厦门·高一期末）已知函数()()11f x x x a =-⋅--，a R ∈．(1)若0a =，解不等式()1f x <；(2)若函数()f x 恰有三个零点1x ，2x ，3x ，求123111x x x ++的取值范围．【解析】(1)当0a =时，原不等式可化为()120x x -⋅-<…①．（ⅰ）当0x ≥时，①式化为220x x --<，解得12x -<<，所以02x ≤<；（ⅱ）当0x <时，①式化为220x x -+>，解得x ∈R ，所以0x <．综上，原不等式的解集为(),2-∞．(2)依题意，()()()2211,11,x a x a x af x x a x a x a ⎧-++--<⎪=⎨-++-≥⎪⎩．因为()10f a =-<，且二次函数()211y x a x a =-++-开口向上，所以当x a ≥时，函数()f x 有且仅有一个零点．所以x a <时，函数()f x 恰有两个零点．所以()()()21,21410,10.a a a a f a +⎧<⎪⎪⎪=+-+>⎨⎪=-<⎪⎪⎩解得3a >．不妨设123x x x <<，所以1x ，2x 是方程()2110x a x a -++--=的两相异实根，则12121,1x x a x x a +=+⎧⎨=+⎩，所以121212111x x x x x x ++==．因为3x 是方程()2110x a x a -++-=的根，且312a x +>，由求根公式得3x =因为函数()g a ()3,+∞上单调递增，所以()332x g >=31012x <<-．所以123111x x x ++．所以a 的取值范围是21,22⎛- ⎝⎭．【过关测试】一、单选题1．（2022·江苏·高一专题练习）已知p ：a m <（其中R a ∈，m ∈Z ），q ：关于x 的一元二次方程2210ax x ++=有一正一负两个根.若p 是q 的充分不必要条件，则m 的最大值为（）A ．1B ．0C ．1-D ．2【答案】C【解析】因为2210ax x ++=有一正一负两个根，所以224010a a ⎧∆=->⎪⎨<⎪⎩，解得0a <.因为p 是q 的充分不必要条件，所以0m <，且m ∈Z ，则m 的最大值为1-.故选：C2．（2022·江苏·高一专题练习）已知方程2(2)50x m x m +-+-=有两个不相等的实数根，且两个实数根都大于2，则实数m 的取值范围是（）A ．(5,4)(4,)--+∞B ．(5,)-+∞C ．(5,4)--D ．(4,2)(4,)--+∞【答案】C【解析】令()2(2)5mf x m x x =+-+-由题可知：()()()()2Δ02450442222242250520m m m m m m m m m m f >⎧⎧--⨯->><-⎧⎪⎪-⎪⎪>⇒<-⇒<-⎨⎨⎨⎪⎪⎪+-⨯+->>-⎩>⎩⎪⎩或则54m -<<-，即(5,4)m ∈--故选：C3．（2021·北京·北师大实验中学高一期中）设方程2610x x -+=的两个不等实根分别为12,x x ，则12||x x -=（）A ．3B ．6C．D．【答案】D【解析】2610x x -+=，364320∆=-=>，故121261x x x x +=⎧⎨=⎩，12||x x -===.故选：D.4．（2021·江苏·高一课时练习）设a 为实数，若方程220x ax a -+=在区间(1,1)-上有两个不相等的实数解，则a 的取值范围是（）.A ．(,0)(1,)-∞⋃+∞B ．(1,0)-C ．1,03⎛⎫- ⎪⎝⎭D ．1,0(1,)3⎛⎫-+∞ ⎪⎝⎭【答案】C【解析】令2()2g x x ax a =-+，由方程220x ax a -+=在区间(1,1)-上有两个不相等的实数解可得244011(1)0(1)0a a a g g ⎧∆=->⎪-<<⎪⎨->⎪⎪>⎩，即011131a a a a <⎧⎪-<<⎪⎪⎨>-⎪⎪<⎪⎩或111131a a a a >⎧⎪-<<⎪⎪⎨>-⎪⎪<⎪⎩，解得103-<<a ，故选：C5．（2022·全国·高一课时练习）一元二次方程()22100ax x a ++=≠有一个正实数根和一个负实数根的一个充分不必要条件是()A ．0a <B ．0a >C ．1a <-D ．2a <【答案】C【解析】由题意，不妨设2()21f x ax x =++，因为(0)10=>f ，且()22100ax x a ++=≠有一个正实数根和一个负实数根，所以2()21f x ax x =++的图像开口向下，即0a <，故对于选项ABCD ，只有C 选项：1a <-是0a <的充分不必要条件.故选：C.6．（2021·四川·树德中学高一阶段练习）设集合{}2320A x x x =-+<，集合{}2210B x ax x =--=，若A B ⋂≠∅，则实数a 的取值范围是（）A ．34,43⎡⎫⎪⎢⎣⎭B ．5,34⎛⎫ ⎪⎝⎭C ．3,4⎡⎫+∞⎪⎢⎣⎭D ．(1,)+∞【答案】B【解析】由题意，{}2320{|12}A x x x x x =-+<=<<若AB ⋂≠∅，即方程2210ax x --=存在根在区间(1,2)（1）若102102a x x =∴--=∴=-，不成立；（2）若0a ≠，由于0x =不为方程的根，故0x ≠，则222221211210(1)1x ax x a x x x x+--=⇔==+=+-由于21115(1,2)(,1)(1)1(,3)24x x x ∈∴∈∴+-∈综上，实数a 的取值范围是5,34⎛⎫⎪⎝⎭故选：B7．（2022·全国·高一课时练习）要使关于x 的方程()22120x a x a +-+-=的一根比1大且另一根比1小，则实数a 的取值范围是（）A ．{}12a a -<<B ．{}21a a -<<C ．{}2a a <-D ．{}1a a >【答案】B【解析】由题意可得()2211220a a a a +-+-=+-<，解得21a -<<.故选：B.8．（2021·甘肃·天水市第一中学高一阶段练习）已知一元二次方程2(1)10()x m x m Z +++=∈有两个实数根1x ，2x ，且12013x x <<<<，则m 的值为（）A ．4-B ．5-C ．6-D ．7-【答案】A【解析】因为元二次方程2(1)10()x m x m Z +++=∈有两个实数根1x ，2x ，且12013x x <<<<，令2()(1)1f x x m x =+++，则由题意可得(0)0(1)0(3)0f f f >⎧⎪<⎨⎪>⎩，即10,30,1330,m m >⎧⎪+<⎨⎪+>⎩解得1333m -<<-，又m Z ∈，可得4m =-.故选：A 二、多选题9．（2022·江苏南通·高一开学考试）已知不等式20(0)x ax b a ++>>的解集是{}|x x d ≠，则下列四个结论中正确的是（）.A ．24a b=B ．若不等式2+x ax b c +<的解集为(3,1)-，则7a b c ++=C ．若不等式20x ax b +-<的解集为12(,)x x ，则120x x >D ．若不等式2x ax b c ++<的解集为12(,)x x ，且12||4x x -=，则4c =【答案】ABD【解析】由题意，不等式20(0)x ax b a ++>>的解集是{}|x x d ≠，所以240a b ∆=-=，24a b ∴=，所以A 正确；对于B ：2+x ax b c +<变形为2+0x ax b c +-<，其解集为(3,1)-，所以231 314 a b c a b -+=-⎧⎪-⨯=-⎨⎪=⎩，得214a b c =⎧⎪=⎨⎪=⎩，故7a b c ++=成立，所以B 正确；对于C ：若不等式20x ax b +-<的解集为12(,)x x ，由韦达定理知：21204a x xb =-=-<，所以C 错误；对于D ：若不等式2x ax bc ++<的解集为12(,)x x ，即20x ax b c ++-<的解集为12(,)x x ，由韦达定理知：21212,4a x x a x x b c c +=-=-=，则12||4x x -==，解得4c =，所以D 正确.故选：D.10．（2021·江苏·海安高级中学高一阶段练习）一元二次方程240x x m -+=有正数根的充分不必要条件是（）A ．4m =B ．5m =C ．1m =D ．12=-m 【答案】ACD【解析】设()24f x x x m =-+，则二次函数()f x 的图象的对称轴为2x =．当4m =时，方程即()224420x x x -+=-=，求得2x =，满足方程有正根，但由方程240x x m -+=有正数根，可得()240f m =-≤，即4m ≤，故4m =是方程240x x m -+=有正数根的充分不必要条件，故A 满足条件；当5m =时，方程即()224521x x x -+=-=-，求得x ∈∅，不满足方程有正实数根，故5m =不是方程240x x m -+=有正数根的充分条件，故排除B ．当1m =时，方程即()224123x x x -+=-=，求得2=±x 但由方程240x x m -+=有正数根，可得()240f m =-≤，即4m ≤，故1m =方程240x x m -+=有正数根的充分不必要条件，故C 满足条件；当12=-m 时，方程即24120x x --=，求得2x =-，或6x =，满足方程有正根，但由方程240x x m -+=有正数根，可得()240f m =-≤，即4m ≤，故12=-m 方程240x x m -+=有正数根的充分不必要条件，故D 满足条件，故选：ACD ．11．（2022·湖南湖南·高一期末）若方程220x x λ++=在区间()1,0-上有实数根，则实数λ的取值可以是（）A ．3-B ．18C ．14D ．1【答案】BC【解析】由题意22x x λ=--在(1,0)-上有解．∵(1,0)x ∈-，∴222(1)1(0,1)x x x λ=--=-++∈，故选：BC ．12．（2021·全国·高一专题练习）已知关于x 的方程()230x m x m +-+=，则下列结论中正确的是（）A ．方程()230x m x m +-+=有一个正根一个负根的充要条件是{}0m m m ∈<B ．方程()230x m x m +-+=有两个正实数根的充要条件是{}01m m m ∈<≤C ．方程()230x m x m +-+=无实数根的充要条件是{}1m m m ∈>D ．当m =3时，方程()230x m x m +-+=的两个实数根之和为0【答案】AB【解析】对A ，当0x =时，函数2(3)y x m x m =+-+的值为m ，由二次函数的图象知，方程有一正一负根的充要条件是{}|0m m m ∈<，故A 正确；对B ，若方程()230x m x m +-+=有两个正实数根1x ，2x ，即()2121234030,0,m m x x m x x m ⎧∆=--≥⎪+=->⎨⎪=>⎩解得：01m <≤，故B 正确；对C ，方程()230x m x m +-+=无实数根，即()2340m m ∆=--<，解得：19m <<，方程()230x m x m +-+=无实数根的充要条件是{}19m m m ∈<<，故C 错误；对D ，当3m =时，方程为230x +=，无实数根，故D 错误.故答案为：AB.13．（2021·江苏·高一专题练习）已知一元二次方程()()21102x m x m Z +++=∈有两个实数根12,x x ，且12013x x <<<<，则m 的值为（）A ．-2B ．-3C ．-4D ．-5【答案】BC 【解析】设()()2112f x x m x =+++，由12013x x <<<<，可得()()()()10200110110230193102f f m f m ⎧>⎪⎧>⎪⎪⎪<⇒+++<⎨⎨⎪⎪>⎩⎪+++>⎪⎩，解得：25562m -<<-，又因为m Z ∈，得3m =-或4m =-，故选：BC.三、填空题14．（2022·安徽省蚌埠第三中学高一开学考试）关于x 的方程210x ax ++=的一根大于1，一根小于1，则a 的取值范围是：__________________．【答案】a <-2【解析】∵关于x 的方程210x ax ++=的一根大于1，另一根小于1，令2()1=++f x x ax ，则(1)20f a =+<，求得2a <-，故答案为：2a <-15．（2021·北京师大附中高一期中）若关于x 的一元二次方程2240x ax -+=有两个实根，且一个实根小于1，另一个实根大于2，则实数a 的取值范围是________．【答案】（52，＋∞）【解析】设2()24f x x ax =-+，由题意2Δ4160(1)1240(2)4440a f a f a ⎧=->⎪=-+<⎨⎪=-+<⎩，解得52a >，故答案为：5(,)2+∞．16．（2021·上海·复旦附中高一期中）若关于x 的方程220x kx -+=的一根大于－1，另一根小于－1，则实数k 的取值范围为______．【答案】(),3-∞-【解析】由题意，关于x 的方程220x kx -+=的一根大于-1，另一根小于-1，设()22f x x kx =-+，根据二次函数的性质，可得()130f k -=+<，解得3k <-，所以实数k 的取值范围为(),3-∞-.故答案为：(),3-∞-.17．（2020·上海·高一专题练习）已知集合()(){}2|320,A x x x x x R =-+-≤∈，{}2|120,B x x ax x R =--≤∈，若A B ⊆，则实数a 的取值范围是______________．【答案】[]1,1-【解析】由()()2320x x x -+-≤，得23020x x x ⎧-≥⎪⎨+-≤⎪⎩或23020x x x ⎧-≤⎪⎨+-≥⎪⎩，解得13x ≤≤，所以集合{|31A x x =-≤≤-或}13x ≤≤，因为A B ⊆，令()212f x x ax =--，则()()3030f f ⎧-≤⎪⎨≤⎪⎩，即9312093120a a +-≤⎧⎨--≤⎩，解得11a -≤≤，所以实数a 的取值范围是[]1,1-故答案为：[]1,1-四、解答题18．（2022·全国·高一期中）命题:p 关于x 的方程20x x m ++=有两个相异负根；命题():0,q x ∃∈+∞，2390x mx -+<．(1)若命题q 为假命题，求实数m 的取值范围；(2)若这两个命题有且仅有一个为真命题，求实数m 的取值范围．【解析】（1）若命题q 为假命题，则对()0,x ∀∈+∞，2390x mx -+≥为真命题；239mx x ∴≤+，即93m x x ≤+；96x x +≥（当且仅当9x x =，即3x =时取等号），36m ∴≤，解得：2m ≤，∴实数m 的取值范围为(],2-∞.（2）由（1）知：若命题q为真命题，则2m >；若命题p 为真命题，则Δ1400m m =->⎧⎨>⎩，解得：104m <<；若p 真q 假，则104m <<；若p 假q 真，则2m >；综上所述：实数m 的取值范围为()10,2,4⎛⎫+∞ ⎪⎝⎭.19．（2022·湖南·高一课时练习）若一元二次方程2570x x a --=的一个根在区间()1,0-内，另一个根在区间()1,2内，求实数a 的取值范围．【解析】令2()57f x x x a =--，则根据题意得(1)057012(0)000(1)0202(2)0201406f a a f a a f a a f a a ->⇒+->⇒<⎧⎪<⇒-⇒⎪⎨<⇒--⇒-⎪⎪>⇒-->⇒<⎩，∴06a <<.故实数a 的取值范围(0,6).20．（2021·辽宁·昌图县第一高级中学高一期中）1.已知()()2213f x x a x =+-+．(1)如果方程()0f x =在()0,3有两个根，求实数a 的取值范围；(2)如果[]1,2x ∃∈，()0f x >成立，求实数a 的取值范围．【解析】(1)()()2213f x x a x =+-+的对称轴为1x a=-要想方程()0f x =在()0,3有两个根，需要满足()()()100001330f a f a f ⎧-<⎪>⎪⎨<-<⎪⎪>⎩解得：(1,1a ∈--(2)[]1,2x ∃∈，()22130x a x +-+>成立，即3122x a x ⎛⎫->-+ ⎪⎝⎭在[]1,2x ∈上有解，只需1a -大于()322x g x x ⎛⎫=-+ ⎪⎝⎭的最小值，其中()322x g x x ⎛⎫=-+ ⎪⎝⎭为对勾函数，在x ⎡∈⎣上单调递增，在)x ∈上单调递减，又()131222g ⎛⎫=-+=- ⎪⎝⎭，()2372244g ⎛⎫=-+=- ⎪⎝⎭，所以最小值为()12g =-故12a ->-，解得：1a >-，实数a 的取值范围为()1,-+∞21．（2021·上海市七宝中学高一阶段练习）设二次函数()2f x ax bx c =++，其中R a b c ∈、、.(1)若()21,94b a c a =+=+，且关于x 的不等式()28200-+<x x f x 的解集为R ，求a 的取值范围；(2)若Z a b c ∈、、，且()()01f f 、均为奇数，求证：方程()0f x =无整数根；(3)若21,21,a b k c k ==-=，当方程()0f x =有两个大于1的不等根时求k 的取值范围.【解析】（1）∵()22820440x x x -+=-+>∴()()221940f x ax a x a =++++<在R 上恒成立∵0a ≠，则()()20Δ414940a a a a <⎧⎪⎨=+-+<⎪⎩，解得12a <-综上所述：a 的取值范围为1,2⎛⎫-∞- ⎪⎝⎭.（2）∵()()0,1f c f a b c ==++，则c 为奇数，a b +为偶数当Z x ∈时，则有：1.若a b 、均为偶数时，则2ax bx +为偶数∴()20f x ax bx c =++≠，即方程()0f x =无整数根2.若a b 、均为奇数时，则有①若x 为偶数时，则2ax bx +为偶数∴()20f x ax bx c =++≠，即方程()0f x =无整数根②若x 为奇数时，则()2ax bx x ax b +=+为偶数∴()20f x ax bx c =++≠，即方程()0f x =无整数根综上所述：方程()0f x =无整数根（3）()()2221f x x k x k =+-+由题意可得()()222Δ21402112120k k k f k k ⎧=-->⎪-⎪->⎨⎪=+>⎪⎩，解得2k <-则k 的取值范围为(),2∞--.。

中考数学专项练习一元二次方程的根（含解析）【一】单项选择题1.假设方程x2-c=0的一个根为-3，那么方程的另一个根为〔〕A.3B.-3C.9D.-2.方程4x2﹣kx+6=0的一个根是2，那么k的值和方程的另一个根分别是〔〕A.5，B.11，C.11，﹣D.5，﹣3.1是关于x的一元二次方程(m－1)x2+x+1=0的一个根，那么m的值是〔〕A.1B.－1C.0D.无法确定4.以下一元二次方程有两个相等实数根的是〔〕A.B.C.D.5.x=-1是关于x的方程2x2+ax-a2=0的一个根，那么a为〔〕A.1B.2C.3D.-2或16.关于x的方程x2+m2x﹣2=0的一个根是1，那么m的值是〔〕A.1B.2C.±1D.±27.假设方程x2-5x=0的一个根是a，那么a2-5a+2的值为〔〕A.-2B.0C.2D.48.一元二次方程的两根是，那么这个方程可以是()A.B.C.D.9.假设n〔〕是关于x的方程的根，那么m＋n的值为A.1B.2C.－1D.－210.关于的方程的一个根为，那么的值为〔〕A.B.C.D.11.x=1是一元二次方程x2-2mx+1=0的一个解，那么m的值是〔〕A.1B.0C.0或1D.0或-112.假设x=2是关于一元二次方程﹣x2++a2=0的一个根，那么a的值是〔〕A.1或4B.1或﹣4C.﹣1或﹣4D.﹣1或413.关于x的一元二次方程〔m﹣1〕x2+6x+m2﹣1=0有一个根是0，那么m取值为〔〕A.1B.﹣1C.±1D.014.假设x=3是关于x的方程x2﹣bx﹣3a=0的一个根，那么a+b的值为〔〕A.3B.-3C.9D.-915.一元二次方程ax2+x+c=0，假设4a-2b+c=0，那么它的一个根是〔〕A.-2B.C.-4D.216.以下方程中解为x=0的是〔〕A.2x+3=2x+1 B.5x=3x C.+4=5 x D.x+1=017.假设c〔c≠0〕为关于x的一元二次方程x2+bx+c=0的根，那么c+ b的值为〔〕A.1B.﹣1C.2D.﹣218. ＝2是关于的方程的一个解，那么2a-1的值是〔〕A.3B.4C.5D.6【二】填空题19.x=1是方程x2+mx+3=0的一个实数根，那么m的值是________．20.假设a是关于方程x2﹣2019x+1=0的一个根，那么a+ =________．21.假设一元二次方程ax2﹣bx﹣2019=0有一根为x=﹣1，那么a+b=__ ______．22.一元二次方程x2+px﹣2=0的一个根为2，那么p的值________【三】计算题23.解方程x2+6x+1=0．24.解方程：2x2+3x﹣5=0．25.解方程组：．26.x=1是一元二次方程〔a﹣2〕x2+〔a2﹣3〕x﹣a+1=0的一个根，求a的值．27.关于x的一元二次方程x2﹣〔k+1〕x﹣6=0的一个根为2，求k的值及另一个根．28.解方程：x2﹣2〔x+4〕=0．【四】解答题29.一元二次方程〔m﹣1〕x2+7mx+m2+3m﹣4=0有一个根为零，求m 的值．30.关于x的方程x2﹣〔k+1〕x﹣6=0的一个根是2，求k的值和方程的另一根．31.定义：如果两个一元二次方程有且只有一个相同的实数根，我们称这两个方程为〝友好方程〞．如果关于x的一元二次方程x2﹣4x+5m=mx+ 5与x2+x+m﹣1=0互为〝友好方程〞，求m的值．【五】综合题32.：x2+3x+1=0．求：〔1〕x+ ；〔2〕x2+ ．33.关于x的一元二次方程x2+2〔k﹣1〕x+k2﹣1=0有两个不相等的实数根．〔1〕求实数k的取值范围；〔2〕0可能是方程的一个根吗？假设是，请求出它的另一个根；假设不是，请说明理由．34.如图，抛物线y=x2+x﹣2与x轴交于A，B两点，与y轴交于点C、〔1〕求点A，点B和点C的坐标；〔2〕在抛物线的对称轴上有一动点P，求PB+PC的值最小时的点P的坐标；〔3〕假设点M是直线AC下方抛物线上一动点，求四边形ABCM面积的最大值．【一】单项选择题1.假设方程x2-c=0的一个根为-3，那么方程的另一个根为〔〕A.3B.-3C.9D.-【考点】一元二次方程的解【解析】【分析】根据一元二次方程的解的定义，将x=-3代入方程x2-c=0，求得c的值；然后利用直接开平方法求得方程的另一根．【解答】∵方程x2-c=0的一个根为-3，∴x=-3满足方程x2-c=0，∴〔-3)2-c=0，解得，c=9；∴x2=9，∴x=±3，解得，x1=3，x2=-3；故方程的另一根是3；应选A、2.方程4x2﹣kx+6=0的一个根是2，那么k的值和方程的另一个根分别是〔〕A.5，B.11，C.11，﹣D.5，﹣【考点】一元二次方程的解【解析】【解答】解：把x=2代入方程4x2﹣kx+6=0，得4×22﹣2k+6 =0，解得k=11，再把k=11代入原方程，得4x2﹣11x+6=0，解得x=2或，那么k=11，另一个根是x=．应选B、【分析】根据一元二次方程的解的定义，把x=2代入方程得到k的值，再计算另外一个根，即可求解．3.1是关于x的一元二次方程(m－1)x2+x+1=0的一个根，那么m的值是〔〕A.1B.－1C.0D.无法确定【考点】一元二次方程的解【解析】【分析】由题意把x=1代入方程(m－1)x2+x+1=0即可得到关于m的方程，解出即可。

初中数学竞赛辅导资料（45）一元二次方程的根甲内容提要1. 一元二次方程ax 2+bx+c=0(a ≠0)的实数根，是由它的系数a, b, c 的值确定的.根公式是：x=aac b b 242-±－. (b 2－4ac ≥0)2. 根的判别式① 实系数方程ax 2+bx+c=0(a ≠0)有实数根的充分必要条件是：b 2－4ac ≥0.② 有理系数方程ax 2+bx+c=0(a ≠0)有有理数根的判定是：b 2－4ac 是完全平方式⇔方程有有理数根.③整系数方程x 2+px+q=0有两个整数根⇔p 2－4q 是整数的平方数.3. 设x 1, x 2 是ax 2+bx+c=0的两个实数根，那么① ax 12+bx 1+c=0 (a ≠0，b 2－4ac ≥0)， ax 22+bx 2+c=0 (a ≠0， b 2－4ac ≥0)；② x 1=a ac b b 242-＋－， x 2=aac b b 242-－－ (a ≠0, b 2－4ac ≥0)；③ 韦达定理：x 1+x 2= a b －, x 1x 2=ac (a ≠0, b 2－4ac ≥0). 4. 方程整数根的其他条件整系数方程ax 2+bx+c=0 (a ≠0)有一个整数根x 1的必要条件是：x 1是c 的因数. 特殊的例子有：C=0⇔x 1=0 ， a+b+c=0⇔x 1=1 ， a －b+c=0⇔x 1=－1. 乙例题例1. 已知：a, b, c 是实数，且a=b+c+1.求证：两个方程x 2+x+b=0与x 2+ax+c=0中，至少有一个方程有两个不相等的实数根.（1990年泉州市初二数学双基赛题）证明 （用反证法）设 两个方程都没有两个不相等的实数根， 那么△1≤0和△2≤0.即⎪⎩⎪⎨⎧++=≤-≤ ③ ② ①－1040412c b a c a b 由①得b ≥41，b+1 ≥45代入③，得 a －c=b+1≥45， 4c ≤4a －5 ④②＋④：a 2－4a+5≤0，即（a －2）2+1≤0，这是不能成立的.既然△1≤0和△2≤0不能成立的，那么必有一个是大于0.∴方程x 2+x+b=0与x 2+ax+c=0中，至少有一个方程有两个不相等的实数根. 本题也可用直接证法：当△1＋△2＞0时，则△1和△2中至少有一个是正数.例2. 已知首项系数不相等的两个方程：（a －1）x 2－(a 2+2)x+(a 2+2a)=0和 (b －1)x 2－(b 2+2)x+(b 2+2b)=0 (其中a,b 为正整数) 有一个公共根. 求a, b 的值.（1989年全国初中数学联赛题）解：用因式分解法求得：方程①的两个根是 a 和12-+a a ； 方程②两根是b 和12-+b b . 由已知a>1, b>1且a ≠b. ∴公共根是a=12-+b b 或b=12-+a a . 两个等式去分母后的结果是一样的.即ab －a=b+2, ab －a －b+1=3, (a －1)(b －1)=3.∵a,b 都是正整数， ∴ ⎩⎨⎧=-3111b a ＝－； 或⎩⎨⎧=-1131b a ＝－.解得⎩⎨⎧=42b a ＝； 或⎩⎨⎧==24b a .又解： 设公共根为x 0那么⎪⎩⎪⎨⎧=+++--=+++--　②（　①0)2()2()10)2()2()1(22202220b b x b x b a a x a x a 先消去二次项： ①×（b －1）－②×（a －1） 得［－（a 2+2）(b －1)+(b 2+2)(a －1)］x 0+(a 2+2a)(b －1)－(b 2+2b)(a －1)=0.整理得 （a －b ）(ab －a －b －2)(x 0－1)=0.∵a ≠b∴x 0＝1； 或 (ab －a －b －2)＝0. 当x 0＝1时，由方程①得 a=1, ∴a －1=0，∴方程①不是二次方程. ∴x 0不是公共根.当(ab －a －b －2)＝0时， 得(a －1)(b －1)=3 ……解法同上.例3. 已知：m, n 是不相等的实数，方程x 2+mx+n=0的两根差与方程y 2+ny+m=0的两根差相等.求：m+n 的值. （1986年泉州市初二数学双基赛题） 解：方程①两根差是21x x -＝221)x x -（＝212214)(x x x x -+＝n m 42-同理方程②两根差是21y y -＝m n 42-依题意，得n m 42-＝m n 42-.两边平方得：m 2－4n=n 2－4m. ∴（m －n ）(m+n+4)=0∵m ≠n ，∴ m+n+4＝0， m+n ＝－4.例4. 若a, b, c 都是奇数，则二次方程ax 2+bx+c=0(a ≠0)没有有理数根. 证明：设方程有一个有理数根nm（m, n 是互质的整数）. 那么a(n m )2+b(nm )+c=0, 即an 2+bmn+cm 2=0. 把m, n 按奇数、偶数分类讨论，∵m, n 互质，∴不可能同为偶数.① 当m, n 同为奇数时，则an 2+bmn+cm 2是奇数＋奇数＋奇数＝奇数≠0；② 当m 为奇数, n 为偶数时，an 2+bmn+cm 2是偶数＋偶数＋奇数＝奇数≠0；③ 当m 为偶数, n 为奇数时，an 2+bmn+cm 2是奇数＋偶数＋偶数＝奇数≠0. 综上所述不论m, n 取什么整数，方程a(n m )2+b(nm)+c=0都不成立. 即 假设方程有一个有理数根是不成立的. ∴当a, b, c 都是奇数时，方程ax 2+bx+c=0(a ≠0)没有有理数根.例5. 求证：对于任意一个矩形A ，总存在一个矩形B ，使得矩形B 与矩形A 的周长比和面积比都等于k (k ≥1). （1983年福建省初中数学竞赛题） 证明：设矩形A 的长为a, 宽为b ，矩形B 的长为c, 宽为d. 根据题意，得k abcdb a dc ==++. ∴c+d=(a+b)k, cd=abk.由韦达定理的逆定理，得c, d 是方程z 2－(a+b)kz+abk=0 的两个根.△ ＝［－（a+b ）k ］2－4abk＝（a 2+2ab+b 2）k 2－4abk=k ［(a 2+2ab+b 2)k －4ab ］∵k ≥1，a 2+b 2≥2ab, ∴a 2+2ab+b 2≥4ab ，(a 2+2ab+b 2)k ≥4ab.∴△≥0.∴一定有c, d 值满足题设的条件.即总存在一个矩形B ，使得矩形B 与矩形A 的周长比和面积比都等于k (k ≥1). 例6. k 取什么整数值时，下列方程有两个整数解？①（k 2－1）x 2－6(3k －1)x+72=0 ； ②kx 2+(k 2－2)x －(k+2)=0. 解：①用因式分解法求得两个根是：x 1=112+k ， x 2=16－k . 由x 1是整数，得k+1=±1, ±2, ±3, ±4, ±6, ±12.由x 2是整数，得k －1=±1, ±2, ±3, ±6.它们的公共解是：得k=0, 2, －2, 3, －5.答：当k=0, 2, －2, 3, －5时，方程①有两个整数解. ②根据韦达定理⎪⎪⎩⎪⎪⎨⎧--=+-=+-=--=+k k k k x x k k k k x x 222221221 ∵x 1, x 2, k 都是整数，∴k=±1，±2. （这只是整数解的必要条件，而不是充分条件，故要进行检验.） 把k=1,－1, 2, －2， 分别代入原方程检验，只有当k=2和k=－2 时适合. 答：当k 取2和－2时，方程②有两个整数解. 丙练习451. 写出下列方程的整数解：① 5x 2－3x=0的一个整数根是＿＿＿.② 3x 2+(2－3)x －2=0的一个整数根是＿＿＿.③ x 2+(5+1)x+5=0的一个整数根是＿＿＿.2. 方程（1－m ）x 2－x －1=0 有两个不相等的实数根，那么整数m 的最大值是＿＿＿＿.3. 已知方程x 2－(2m －1)x －4m+2=0 的两个实数根的平方和等于5，则m=＿＿＿.4. 若x ≠y ，且满足等式x 2+2x －5=0 和y 2+2y －5=0. 那么yx 11+＝＿＿＿.（提示：x, y 是方程z 2+5z －5=0 的两个根.） 5. 如果方程x 2+px+q=0 的一个实数根是另一个实数根的2倍，那么p, q 应满足的关系是：＿＿＿＿＿＿＿＿＿＿＿. （1986年全国初中数学联赛题）6. 若方程ax 2+bx+c=0中a>0, b>0, c<0. 那么两实数根的符号必是＿＿＿＿＿＿.（1987年泉州市初二数学双基赛题）7. 如果方程mx 2－2(m+2)x+m+5=0 没有实数根，那么方程（m －5）x 2－2mx+m=0实数根的个数是（ ）.(A)2 （B ）1 （ C ）0 （D ）不能确定 （1989年全国初中数学联赛题）8. 当a, b 为何值时，方程x 2+2(1+a)x+(3a 2+4ab+4b 2+2)=0 有实数根？（1987年全国初中数学联赛题）9. 两个方程x 2+kx －1=0和x 2－x －k=0有一个相同的实数根，则这个根是（ ）(A)2 （B ）－2 （C ）1 （D ）－1 （1990年泉州市初二数学双基赛题）10. 已知：方程x 2+ax+b=0与x 2+bx+a=0仅有一个公共根，那么a, b 应满足的关系是：＿＿＿＿＿＿＿＿＿＿＿.11. 已知：方程x 2+bx+1=0与x 2－x －b=0有一个公共根为m ，求：m ，b 的值.12. 已知：方程x 2+ax+b=0的两个实数根各加上1，就是方程x 2－a 2x+ab=0的两个实数根.试求a, b 的值或取值范围. （1997年泉州市初二数学双基赛题）13. 已知：方程ax 2+bx+c=0(a ≠0)的两根和等于s 1，两根的平方和等于s 2, 两根的立方和等于s 3.求证：as 3+bs 2+cs 1=0.14. 求证：方程x 2－2(m+1)x+2(m －1)=0 的两个实数根，不能同时为负.（可用反证法）15. 已知：a, b 是方程x 2+mx+p=0的两个实数根；c, d 是方程x 2+nx+q=0 的两个实数根.求证：（a －c ）(b －c)(a －d)(b －d)=(p －q)2. 16. 如果一元二次方程的两个实数根的平方和等于5，两实数根的积是2，那么这个方程是：＿＿＿＿＿＿＿＿＿＿. （1990年泉州市初二数学双基赛题）17. 如果方程（x －1）(x 2－2x+m)=0的三个根，可作为一个三角形的三边长，那么实数m的取值范围是 （ ）（A ） 0≤m ≤1 （B ）m ≥43 （C ）43<m ≤1 （D ）43≤m ≤1 （1995年全国初中数学联赛题）18. 方程7x 2－(k+13)x+k 2－k －2=0 (k 是整数)的两个实数根为α，β且0＜α＜1，1＜β＜2，那么k 的取值范围是( )（A ）3<k<4 (B)-2<k<-1 (C) 3<k<4 或-2<k<-1 （D ）无解（1990年全国初中数学联赛题）1. ①0， ②1， ③－12. 03. 1（舍去－2）4.52 5. 9q=2p 26. 一正一负7. D8. a=1,b=－0.59. C10. a+b+1=0, a ≠b 11. m=－1，b=2 12.⎩⎨⎧-=-=⎪⎩⎪⎨⎧≤=.1,241,1b a b a ： 13. 左边＝a(x 13+x 23)+b(x 12+x 22)+c(x 1+x 2)=……14. 用反证法，设x 1<0,x 2<0,由韦达定理推出矛盾（m<－1, m>1） 15. 由韦达定理,把左边化为 p, q16. x 2±3x+2=0 17. C 18. C。

专题04 一元二次方程根的分布二次方程()200ax bx c a ++=≠的根从几何意义上来说就是二次函数()c bx ax x f ++=2与x 轴交点的横坐标，所以研究02=++c bx ax 的实根的情况，可从函数()c bx ax x f ++=2的图象上进行研究.若在()+∞∞-,内研究方程02=++c bx ax 的实根情况，只需考查()c bx ax x f ++=2与x 轴交点的个数以及交点横坐标的符号，根据判别式以及韦达定理，由∆、21x x +、21x x ⋅的值与符号，从而判断出实根的情况.若在区间()n m ,内研究二次方程02=++c bx ax ，则需由二次函数图象与区间关系来确定.知识梳理分布情况两个负根即两根都小于0 ()120,0x x << 两个正根即两根都大于0 ()120,0x x >>一正根一负根即一个根小于0，一个大于0()120x x <<大致图象（0>a ）知识结模块一：得出的结论()00200b a f ∆>⎧⎪⎪-<⎨⎪>⎪⎩()00200b a f ∆>⎧⎪⎪->⎨⎪>⎪⎩()00<f大致图象（0<a ）得出的结论()00200b a f ∆>⎧⎪⎪-<⎨⎪<⎪⎩ ()00200b a f ∆>⎧⎪⎪->⎨⎪<⎪⎩()00>f综合结论（不讨论）()00200b a a f ∆>⎧⎪⎪-<⎨⎪⋅>⎪⎩ ()00200b a a f ∆>⎧⎪⎪->⎨⎪⋅>⎪⎩()00<⋅f a【例1】已知方程()2210x m x m -++=有两个不等正实根，求实数m 的取值范围． 【难度】★★ 【答案】见解析 【解析】由典例剖析()()0102200m f ∆>⎧⎪-+⎪->⎨⎪>⎪⎩⇒()218010m m m m ⎧+->⎪>-⎨⎪>⎩⇒330m m m ⎧<->+⎪⎨>⎪⎩⇒03m <<-3m >+即为所求的范围．【例2】若方程05)2(2=-+-+m x m x 的根满足下列条件，分别求出实数m 的取值范围． （1） 方程两实根均为正数； （2） 方程有一正根一负根． 【难度】★★ 【答案】见解析【解析】分析 讨论二次方程根的分布，应在二次方程存在实根的条件下进行．代数方法与图象法是研究二次方程根的分布问题的主要方法．解1 （1）由题意，得.45244050)2(0)5(4)2(00022121-≤⇒⎪⎩⎪⎨⎧<<≥-≤⇒⎪⎩⎪⎨⎧>->--≥---⇒⎪⎩⎪⎨⎧>>+≥∆m m m m m m m m m x x x x 或所以，当4-≤m 时，原方程两实根均为正数；（2）由题意，得.5050021>⇒<-⇒⎩⎨⎧<≥∆m m x x所以，当5>m 时，原方程有一正根一负根．解2 二次函数m x m x y -+-+=5)2(2的图象是开口向上的抛物线． （1）如图，由题意，得4052)2(4)2(022050)2(020)0(22-≤⇒⎪⎪⎪⎩⎪⎪⎪⎨⎧≤-+--->-->-⇒⎪⎪⎪⎩⎪⎪⎪⎨⎧≤->->m m m m m m a b f a b f 。

2023年初高中衔接素养提升专题课时检测第五讲一元二次方程根的分布（精练）（解析版）（测试时间60分钟）一、单选题（在每小题给出的四个选项中，只有一项是符合题目要求的）1.（2022·四川巴中高一专题检测）若关于x 的一元二次方程2(1)0x m x m -+-=有两个不相等的实根，则m 的取值范围为（）A．((),22-∞---++∞B．(33---+C．((),33-∞---++∞D．(22---+【答案】C 【解析】由关于x 的一元二次方程2(1)0x m x m -+-=有两个不相等的实根，所以2(1)40m m ∆=++=，即26+10m m +>解得：3m >-+或3m <--2.（2022·江苏·高一专题检测）一元二次方程24260x mx m -++=有两个不等的非正根，则实数m 的范围为（）A．30m -<<B．31m -<≤-C．31m -≤<-D．312m -≤≤【答案】C【解析】因为一元二次方程24260x mx m -++=有两个不等的非正根，2164(26)020260m m m m ⎧∆=-+>⎪<⎨⎪+≥⎩，解得31m -≤<-，故选：C 3.（2022·陕西榆林高一专题检测）若方程()2250x m x m ++++=只有正根，则m 的取值范围是（）A．4m ≤-或4m ≥B．54m -<≤-C．54m -≤≤-D．52m -<<-【答案】B 【解析】方程()2250x m x m ++++=只有正根，则1（）当()()22450m m ∆=+-+=，即4m =±时，当4m =-时，方程为()210x -=时，1x =，符合题意；当4m =时，方程为()230x +=时，3x =-不符合题意.故4m =-成立；2（）当()()22450m m ∆=+-+>，解得4m <-或4m >，则()()()224502050m m m m ⎧∆=+-+>⎪-+>⎨⎪+>⎩，解得54m -<<-.综上得54m -<≤-.故选B.4．（2022·江苏·高一月考）设1x ，2x 是关于x 的方程2(1)20x a x a +-++=的根．若111x -<<，212x <<，则实数a 的取值范围是()A ．4(,1)3--B ．31(,)42-C ．(2,1)-D ．(2,1)--【解答】解：由题意知，函数2()(1)2f x x a x a =+-++开口方向向上，若111x -<<，212x <<，则函数须同时满足三个条件：当1x =-时，2(1)20x a x a +-++>，代入解得40>，恒成立；当1x =时，2(1)20x a x a +-++<，代入解得220a +<，1a <-；当2x =时，2(1)20x a x a +-++>，代入解得4340,3a a +>>-，综上，实数a 的取值范围是4(,1)3--．故选：A ．5．（2022·广东深圳高一专题检测）已知一元二次方程2(1)10()x m x m Z +++=∈有两个实数根1x ，2x ，且12013x x <<<<，则m 的值为()A ．4-B ．5-C ．6-D ．7-【解答】解：一元二次方程2(1)10()x m x m Z +++=∈有两个实数根1x ，2x ，且12013x x <<<<，令2()(1)10g x x m x =+++=，则(0)0(1)0(3)0g g g >⎧⎪<⎨⎪>⎩，即10301330m m >⎧⎪+<⎨⎪+>⎩，解得1333m -<<-，m Z ∈ ，4m ∴=-．故选：A ．二、填空题6.（2022·浙江义乌高一专题检测）若关于x 的方程20x x a ++=的一个根大于1、另一个根小于1，则实数a 的取值范围为_____.【答案】(,2)-∞-【解析】 关于x 的方程20x x a ++=的一个根大于1、另一个根小于1，令2()f x x x a =++，则()120f a =+<，解得2a <-，7.（2022·江苏·高一专题检测）已知方程x 2－a 2x －a ＋1＝0的两根x 1，x 2满足0＜x 1＜1，x 2＞1.则实数a的取值范围是．【解析】设f(x)＝x2－a2x－a＋1.(0)＝－a＋1＞0，(1)＝1－a2－a＋1＜0，解得a＜－2.8（2022·甘肃景泰二中高一专题检测）若函数f(x)＝x2＋(m－2)x＋(5－m)有两个小于2的不同零点，则实数m的取值范围是．【解析】＝(m－2)2－4(5－m)＞0，－m－22＜2，(2)＝m＋5＞0，解得m＞4.9.（2022·银川一中高一专题检测）关于x的方程x2＋2(m－1)x＋2m＋6＝0两个实根x1，x2满足x1＜2，x2＞4，则实数m的取值范围是．【解析】设f(x)＝x2＋2(m－1)x＋2m＋6.(2)＝4＋4(m－1)＋2m＋6＜0，(4)＝16＋8(m－1)＋2m＋6＜0，m＋6＜0，m＋14＜0，解得m＜－75.三、解答题（解答时应写出文字说明、证明过程或演算步骤）10（2022·江苏·高一专题检测）方程8x2－(m－1)x＋m－7＝0的两实根都大于1，求实数m 的取值范围．【解析】方法一设函数f(x)＝8x2－(m－1)x＋m－7，作其草图，如图．若两实根均大于1，需m－1)2－32(m－7)≥0，≥25或m≤9，∈R，＞17，解得m≥25.方法二设方程两根分别为x1，x2，则x1＋x2＝m－18，x1x2＝m－78，因为两根均大于1，所以x1－1＞0，x2－1＞0，＝(m－1)2－32(m－7)≥0，x1－1)＋(x2－1)＞0，x1－1)(x2－1)＞0，)2－32(m－7)≥0，－m－18＋1＞0，解得11．（2022·江西高一第一月考）求实数m 的范围，使关于x 的方程22(1)260.x m x m +-++=(1)有两个实根，且一个比2大，一个比2小；(2)有两个实根 αβ，，且满足014αβ<<<<；(3)至少有一个正根.【解析】（1）设()()22126y f x x m x m ==+-++．依题意有()20f <，即()441260m m +-++<，得1m <-．（2）设()()22126y f x x m x m ==+-++．依题意有()()()02601450410140f m f m f m ⎧=+>⎪=+<⎨⎪=+>⎩，解得7554m -<<-．（3）设()()22126y f x x m x m ==+-++．方程至少有一个正根，则有三种可能：①有两个正根，此时可得()()Δ0002102f m ⎧⎪≥⎪⎪>⎨⎪-⎪>⎪-⎩，即153.311m m m m m ≤-≥⎧⎪>-∴-<≤-⎨⎪<⎩或．②有一个正根，一个负根，此时可得()00f <，得3m <-．③有一个正根，另一根为0，此时可得()6203210m m m +=⎧∴=-⎨-<⎩，．综上所述，得1m ≤-．12.（2022·湖北武汉高一课时检测）已知关于x 的方程220x x a -+=．(1)当a 为何值时，方程的一个根大于1，另一个根小于1？(2)当a 为何值时，方程的一个根大于1-且小于1，另一个根大于2且小于3？(3)当a 为何值时，方程的两个根都大于0？【解析】（1）二次函数22y x x a =-+的图象是开口向上的抛物线，故方程220x x a -+=的一个根大于1，另一个根小于1，则2120a -+<，解得1a <，所以a 的取值范围是{}1a a <．（2）方程220x x a -+=的一个根大于1-且小于1，另一个根大于2且小于3，作满足题意的二次函数22y x x a =-+的大致图象，由图知，120120440960a a a a ++>⎧⎪-+<⎪⎨-+<⎪⎪-+>⎩，解得30a -<<．所以a 的取值范围是{}30a a -<<．（3）方程220x x a -+=的两个根都大于0，则Δ4400a a =-≥⎧⎨>⎩，解得01a <≤，所以a 的取值范围是{}01a a <≤．。

2020年高考文科数学总复习：一元二次方程根的分布1．若一元二次方程kx 2＋3kx ＋k －3＝0的两根都是负数，则k 的取值范围为________．答案 (－∞，－125]∪(3，＋∞) 解析 依题意可知⎩⎪⎨⎪⎧Δ≥0，k －3k >0，解得k ≤－125或k>3. 2．一元二次方程kx 2＋3kx ＋k －3＝0有一个正根和一个负根，则k 的取值范围为________． 答案 (0，3)解析 依题意有k －3k<0⇒0<k<3. 3．若一元二次方程kx 2＋(2k －1)x ＋k －3＝0有一根为零，则另一根的符号为________． 答案 负解析 由已知k －3＝0，∴k ＝3，代入原方程得3x 2＋5x ＝0，另一根为负根．4．已知方程x 2－11x ＋m －2＝0的两实根都大于1，则m 的取值范围为________． 答案 12<m ≤1294解析 由题意得应满足⎩⎪⎨⎪⎧Δ≥0，112>1，f （1）>0即⎩⎪⎨⎪⎧112－4（m －2）≥0，m －12>0 解得12<m ≤1294. 5．若一元二次方程mx 2－(m ＋1)x ＋3＝0的两个实根都大于－1，则m 的取值范围为________．答案 m<－2或m ≥5＋2 6解析 由题意得应满足⎩⎪⎨⎪⎧m ≠0，m＋12m >－1，Δ≥0，mf （－1）>0解得：m<－2或m ≥5＋26. 6．若一元二次方程mx 2－(m ＋1)x ＋3＝0的两实根都小于2，则m 的取值范围为________．答案 m<－12或m ≥5＋2 6解析 由题意得，应满足⎩⎪⎨⎪⎧m ≠0，Δ≥0m ＋12m <2，mf （2）>0，解得：m<－12 或m ≥5＋2 6.7．已知方程x 2＋2mx ＋2m 2－3＝0有一根大于2，另一根比2小，则m 的取值范围为________． 答案 －1－22<m<－1＋22 解析 由题意得，应满足f(2)<0，即2m 2＋4m ＋1<0，解得：－1－22<m<－1＋22. 8．已知方程x 2＋(m －2)x ＋2m －1＝0只有一实根在0和1之间，则m 的取值范围为________． 答案 12<m<23解析 由题意得，应满足f(0)f(1)<0，解得12<m<23. 9．已知方程x 2＋(m －2)x ＋2m －1＝0的较大实根在0和1之间，则m 的取值范围为________． 答案 23<m<6－27 解析 由题意得：①⎩⎪⎨⎪⎧f （0）<0，f （1）>0，－m －22<1；或②⎩⎪⎨⎪⎧f （0）>0，f （1）>0，0<－m －22<1，f （－m －22）<0，解得①②得23<m<6－27. 10．若方程x 2＋(k ＋2)x －k ＝0的两实根均在区间(－1，1)内，则k 的取值范围为________．答案 －4＋23≤k<－12解析 由题意得，应满足⎩⎪⎨⎪⎧Δ≥0，－1<－k ＋22<1，f （－1）>0，f （1）>0.解得：－4＋23≤k<－12. 11．若方程x 2＋(k －2)x ＋2k －1＝0的两根中，一根在0和1之间，另一根在1和2之间，则k 的取值范围为________．答案 12<k<23解析 由题意得，应满足⎩⎪⎨⎪⎧f （0）>0f （1）<0，f （2）>0解得12<k<23. 12．已知关于x 的方程(m －1)x 2－2mx ＋m 2＋m －6＝0的两根为α，β且0<α<1<β，则m 的取值范围为________．答案 －3<m<－7或2<m<7解析 由题意得，应满足⎩⎪⎨⎪⎧f （0）f （1）<0（m －1）f （1）<0解得－3<m<－7或2<m<7.。

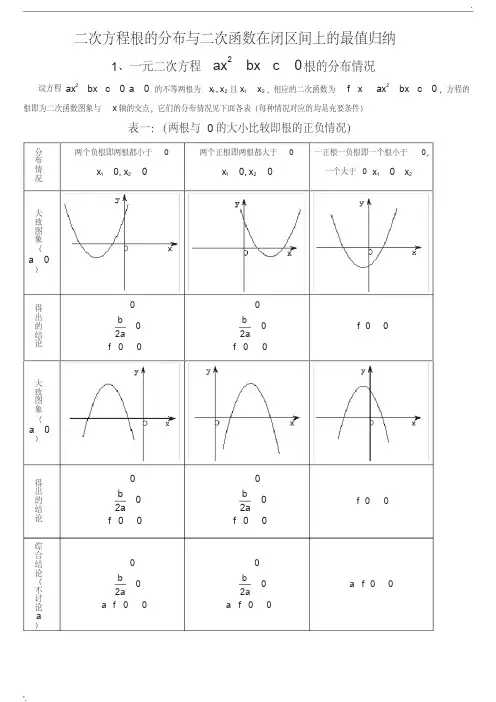
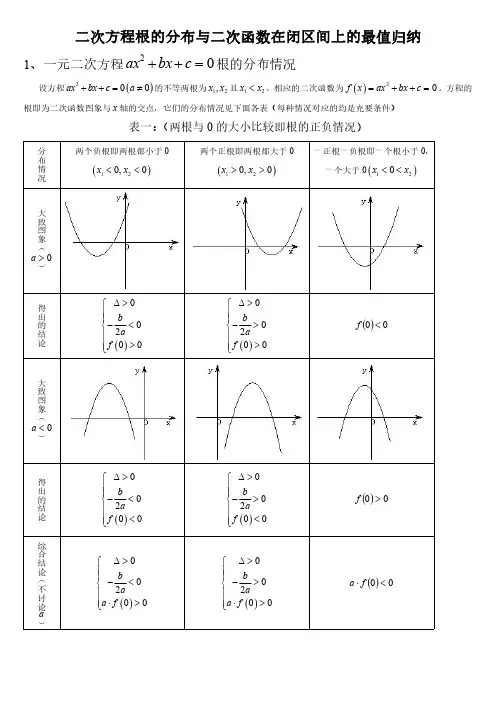
二次方程根的分布与二次函数在闭区间上的最值归纳1、一元二次方程02=++c bx ax 根的分布情况设方程()200ax bx c a ++=≠的不等两根为12,x x 且12x x <，相应的二次函数为()20f x ax bx c =++=，方程的根即为二次函数图象与x 轴的交点，它们的分布情况见下面各表（每种情况对应的均是充要条件）表一：（两根与0的大小比较即根的正负情况）分布情况两个负根即两根都小于0()120,0x x <<两个正根即两根都大于0()120,0x x >>一正根一负根即一个根小于0，一个大于0()120x x <<大致图象（>a ）得出的结论()00200b a f ∆>⎧⎪⎪-<⎨⎪>⎪⎩()00200b a f ∆>⎧⎪⎪->⎨⎪>⎪⎩()00<f 大致图象（<a ）得出的结论()00200b a f ∆>⎧⎪⎪-<⎨⎪<⎪⎩()00200b a f ∆>⎧⎪⎪->⎨⎪<⎪⎩()00>f 综合结论（不讨论a）()00200b a a f ∆>⎧⎪⎪-<⎨⎪⋅>⎪⎩()00200b a a f ∆>⎧⎪⎪->⎨⎪⋅>⎪⎩()00<⋅f a分布情况两根都小于k 即k x k x <<21,两根都大于k 即k x k x >>21,一个根小于k ，一个大于k 即21x k x <<大致图象（>a ）得出的结论()020b k a f k ∆>⎧⎪⎪-<⎨⎪>⎪⎩()020b k a f k ∆>⎧⎪⎪->⎨⎪>⎪⎩()0<k f 大致图象（<a ）得出的结论()020b k a f k ∆>⎧⎪⎪-<⎨⎪<⎪⎩()020b k a f k ∆>⎧⎪⎪->⎨⎪<⎪⎩()0>k f 综合结论（不讨论a）()020b k a a f k ∆>⎧⎪⎪-<⎨⎪⋅>⎪⎩()020b k a a f k ∆>⎧⎪⎪->⎨⎪⋅>⎪⎩()0<⋅k f a kkk分布情况两根都在()n m ,内两根有且仅有一根在()n m ,内（图象有两种情况，只画了一种）一根在()n m ,内，另一根在()q p ,内，qp n m <<<大致图象（>a ）得出的结论()()0002f m f n b m na ∆>⎧⎪>⎪⎪>⎨⎪⎪<-<⎪⎩()()0<⋅n f m f ()()()()0000f m f n f p f q ⎧>⎪<⎪⎨<⎪⎪>⎩或()()()()00f m f n f p f q <⎧⎪⎨<⎪⎩大致图象（<a ）得出的结论()()0002f m f n b m na ∆>⎧⎪<⎪⎪<⎨⎪⎪<-<⎪⎩()()0<⋅n f m f ()()()()0000fm f n f p f q ⎧<⎪>⎪⎨>⎪⎪<⎩或()()()()00f m f n f p f q <⎧⎪⎨<⎪⎩综合结论（不讨论a）——————()()0<⋅n f m f ()()()()⎪⎩⎪⎨⎧<<00q f p f n f m f 根在区间上的分布还有一种情况：两根分别在区间()n m ,外，即在区间两侧12,x m x n <>，（图形分别如下）需满足的条件是（1）0a >时，()()0f m f n <⎧⎪⎨<⎪⎩；（2）0a <时，()()0f m f n >⎧⎪⎨>⎪⎩对以上的根的分布表中一些特殊情况作说明：（1）两根有且仅有一根在()n m ,内有以下特殊情况：若()0f m =或()0f n =，则此时()()0f m f n < 不成立，但对于这种情况是知道了方程有一根为m 或n ，可以求出另外一根，然后可以根据另一根在区间()n m ,内，从而可以求出参数的值。