逻辑函数及其表示方法(案例分析)

逻辑函数的表示方法有( )。

逻辑函数是计算机科学中的重要概念，它被广泛应用于数字电路设计、逻辑推理、人工智能等领域。

逻辑函数可以用多种方式来表示，以下是常用的几种方法：
1. 真值表表示法：真值表是一种表格，用来显示逻辑函数在所有可能的输入条件下的输出结果。

真值表表示法是一种直观的方法，但是对于较大的逻辑函数来说，真值表会变得非常庞大，难于处理。

2. 布尔表达式表示法：布尔表达式是由逻辑运算符和变量组成的表达式，它可以直接表示逻辑函数的含义。

布尔表达式表示法比真值表更精简，便于计算和优化。

3. 逻辑图表示法：逻辑图是一种图形表示法，用来显示逻辑函数的输入和输出之间的关系。

逻辑图表示法可以帮助人们直观地理解逻辑函数的含义，并且可以方便地进行逻辑电路的设计和布局。

4. 卡诺图表示法：卡诺图是一种图形表示法，用来显示逻辑函数的真值表中的重要特征。

卡诺图表示法可以帮助人们快速地进行逻辑函数的化简，从而得到更为简洁的布尔表达式。

总的来说，逻辑函数的不同表示方法各有优缺点，根据具体的应用场
景和需要，选择合适的表示方法可以提高逻辑函数的设计和实现效率。

布尔函数相关理论及其应用布尔函数是数学和计算机科学领域中一个重要的概念。

它被广泛应用于逻辑设计、电路设计、密码学、信息安全等领域。

本文将介绍布尔函数的基本概念、性质以及它在实际应用中的一些例子。

一、布尔函数的定义布尔函数是由布尔变量和逻辑运算符组成的一种函数，它的取值只能是0或1。

布尔变量可以看作逻辑变量，它们代表了逻辑值的真和假。

逻辑运算符包括与、或、非等。

布尔函数可以表示一种逻辑关系，描述了不同变量之间的逻辑连接。

二、布尔函数的性质1. 单调性：对于任意布尔函数f(x1, x2, ..., xn)，如果在某两个向量x 和y中，x的每个元素都小于等于y的对应元素，那么f(x)小于等于f(y)。

换句话说，单调性表示提高一个输入变量的取值会导致输出变量的取值增加或保持不变。

2. 自反性：对于任意布尔函数f(x), f(x')=1-f(x)。

这意味着如果一个布尔函数取真的输入向量x，那么将x的每个元素取反所得到的向量x'将导致函数值取反。

3. 幂等性：对于任意布尔函数f(x), f(x)=f(f(x))。

这表示一个布尔函数与它自己的复合等于它本身。

三、布尔函数的应用1. 逻辑设计：布尔函数被广泛应用于逻辑门电路的设计。

逻辑门将布尔函数的输入映射为输出。

通过组合不同的逻辑门，可以实现复杂的逻辑功能，如加法器、乘法器等。

2. 信息安全：布尔函数在密码学和信息安全领域中起着重要的作用。

它们被用于生成密钥和实现加密算法。

布尔函数的性质可以帮助设计强大的密码算法，抵抗各种攻击。

3. 电路设计：布尔函数被应用于电路设计中，用于描述和优化电路的功能和性能。

通过布尔函数分析和优化，可以提高电路的速度、面积和功耗等指标。

4. 模拟电路的离散化：布尔函数可以将连续的输入变量离散化，从而将模拟电路问题转化为数字逻辑的问题。

这种转化可以简化电路设计和分析的过程。

四、布尔函数应用案例1. DES加密算法：DES（Data Encryption Standard）是一种对称加密算法，它使用了布尔函数来实现复杂的密钥生成和数据变换。

数字电子技术教案一、教学目标1. 知识与技能：（1）理解数字电路的基本概念，包括逻辑门、逻辑函数、逻辑代数等；（2）掌握基本逻辑门电路的原理和应用，包括与门、或门、非门、异或门等；（3）学会使用逻辑门电路实现简单的数字电路功能，如编码器、译码器、半加器等；（4）了解数字电路的设计方法，能够设计简单的数字电路系统。

2. 过程与方法：（1）通过观察、分析逻辑门电路的实物和原理图，培养学生的观察和分析能力；（2）通过动手搭建逻辑门电路，培养学生的实践操作能力；（3）通过设计简单的数字电路，培养学生的创新设计能力。

3. 情感态度与价值观：（1）培养学生对数字电路的兴趣，激发学生学习数字电路的积极性；（2）培养学生团队合作的精神，提高学生沟通协作能力；（3）培养学生勇于探索、严谨治学的科学态度。

二、教学内容1. 数字电路的基本概念（1）逻辑门的概念及其分类；（2）逻辑函数的概念及其表示方法；（3）逻辑代数的概念及其基本运算法则。

2. 基本逻辑门电路（1）与门电路的原理及其应用；（2）或门电路的原理及其应用；（3）非门电路的原理及其应用；（4）异或门电路的原理及其应用。

3. 数字电路的设计方法（1）组合逻辑电路的设计方法；（2）时序逻辑电路的设计方法；（3）数字电路系统的整体设计方法。

三、教学重点与难点1. 教学重点：（1）逻辑门电路的原理及其应用；（2）数字电路的设计方法。

2. 教学难点：（1）逻辑函数的表示方法及其基本运算法则；（2）数字电路系统的整体设计方法。

四、教学方法1. 讲授法：讲解逻辑门电路的原理、逻辑函数的表示方法及数字电路的设计方法；2. 演示法：展示逻辑门电路的实物和原理图，让学生更直观地理解逻辑门电路；3. 实践操作法：让学生动手搭建逻辑门电路，提高学生的实践操作能力；4. 案例分析法：分析实际应用中的数字电路案例，帮助学生更好地理解数字电路的应用。

五、教学准备1. 教学材料：教材、课件、实验器材（如逻辑门电路模块、导线、连接器等）；2. 教学工具：投影仪、电脑、实验桌、示波器等；3. 实验器材：逻辑门电路模块、导线、连接器、开关、灯泡等。

一、公式法化简：是利用逻辑代数的基本公式，对函数进行消项、消因子。

常用方法有：①并项法利用公式AB+AB’=A 将两个与项合并为一个，消去其中的一个变量。

②吸收法利用公式A+AB=A 吸收多余的与项。

③消因子法利用公式A+A’B=A+B 消去与项多余的因子④消项法利用公式AB+A’C=AB+A’C+BC 进行配项，以消去更多的与项。

⑤配项法利用公式A+A=A，A+A’=1配项，简化表达式。

二、卡诺图化简法逻辑函数的卡诺图表示法将n变量的全部最小项各用一个小方块表示，并使具有逻辑相邻性的最小项在几何位置上相邻排列，得到的图形叫做n变量最小项的卡诺图。

逻辑相邻项：仅有一个变量不同其余变量均相同的两个最小项，称为逻辑相邻项。

1.表示最小项的卡诺图将逻辑变量分成两组，分别在两个方向用循环码形式排列出各组变量的所有取值组合，构成一个有2n个方格的图形，每一个方格对应变量的一个取值组合。

具有逻辑相邻性的最小项在位置上也相邻地排列。

用卡诺图表示逻辑函数：方法一：1、把已知逻辑函数式化为最小项之和形式。

2、将函数式中包含的最小项在卡诺图对应的方格中填1，其余方格中填0。

方法二：根据函数式直接填卡诺图。

用卡诺图化简逻辑函数：化简依据：逻辑相邻性的最小项可以合并，并消去因子。

化简规则：能够合并在一起的最小项是2n个。

如何最简：圈数越少越简；圈内的最小项越多越简。

注意：卡诺图中所有的1 都必须圈到，不能合并的1 单独画圈。

说明，一逻辑函数的化简结果可能不唯一。

合并最小项的原则：1）任何两个相邻最小项，可以合并为一项，并消去一个变量。

2）任何4个相邻的最小项，可以合并为一项，并消去2个变量。

3）任何8个相邻最小项，可以合并为一项，并消去3个变量。

卡诺图化简法的步骤：画出函数的卡诺图;画圈（先圈孤立1格；再圈只有一个方向的最小项（1格）组合）；画圈的原则：合并个数为2n；圈尽可能大（乘积项中含因子数最少）；圈尽可能少（乘积项个数最少）；每个圈中至少有一个最小项仅被圈过一次，以免出现多余项。

第二章：布尔代数及其分析数字电路基于排列组合与数字集合论，和数理逻辑有一定距离。

在逻辑函数的计算方面，使用数理逻辑的非计算，能够化简布尔表达式。

布尔逻辑代数引进数字电路,与命题的真假判断有区别,因此逻辑函数用数字函数描述更有广泛的内涵:既包括逻辑计算也包括组合功能.英国数学家布尔的研究导致逻辑代数的出现，并被命名为布尔代数。

逻辑代数给数字电路建立二值逻辑模型,可进行具体数字系统的分析和设计,并在此基础上化简运算,得到数字系统的最优实现方法.使用布尔代数还可以揭示不同逻辑函数之间的相互关系,很清楚的发现这些逻辑函数所对应的具体数字电路之间的转换关系,根据实际需要灵活选择,实现不同数字电路的互换.§1.布尔代数系统的基本内容布尔代数系统建立在集合{0，1}上的运算和规则。

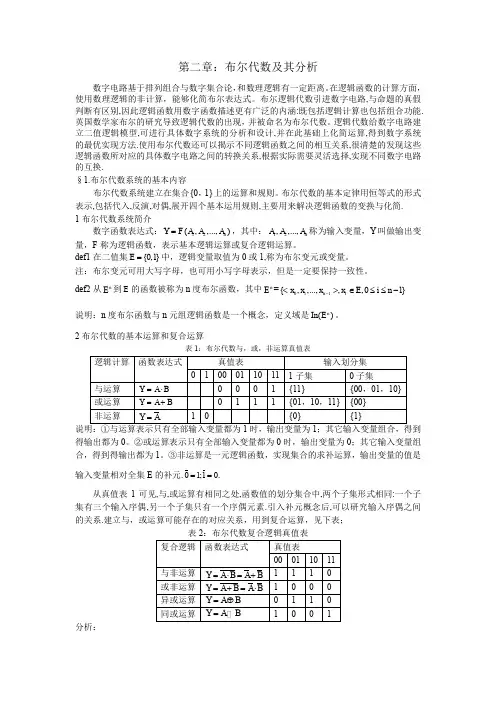
布尔代数的基本定律用恒等式的形式表示,包括代入,反演,对偶,展开四个基本运用规则,主要用来解决逻辑函数的变换与化简. 1布尔代数系统简介数字函数表达式：12(,,...,)n Y F A A A =，其中：12,,...,n A A A 称为输入变量，Y 叫做输出变量，F 称为逻辑函数，表示基本逻辑运算或复合逻辑运算。

def1在二值集{0,1}E =中，逻辑变量取值为0或1,称为布尔变元或变量。

注：布尔变元可用大写字母，也可用小写字母表示，但是一定要保持一致性。

def2从n E 到E 的函数被称为n 度布尔函数，其中n E =011{,,...,,,01}n i x x x x E i n -<>∈≤≤- 说明：n 度布尔函数与n 元组逻辑函数是一个概念，定义域是()n In E 。

2布尔代数的基本运算和复合运算表1：布尔代数与，或，非运算真值表说明：①与运算表示只有全部输入变量都为1时，输出变量为1；其它输入变量组合，得到得输出都为0。

②或运算表示只有全部输入变量都为0时，输出变量为0；其它输入变量组合，得到得输出都为1。

Excel高级函数使用CONCATENATE和IF进行条件文本合并Excel是一种功能强大的电子表格软件，广泛应用于数据处理和分析工作中。

其中，高级函数是Excel中的重要功能之一，能够帮助用户高效地进行数据处理。

在本文中，将介绍如何使用Excel中的CONCATENATE函数和IF函数进行条件文本合并，以便实现更灵活的数据处理需求。

一、CONCATENATE函数的基本使用CONCATENATE函数是Excel中常用的文本合并函数，它可以将多个文本字符串进行拼接。

其基本语法为：=CONCATENATE(text1, text2, ...)其中，text1、text2等为需要合并的文本字符串，可以是文字、数字或其他单元格引用。

例如，我们有两个单元格分别包含姓名和职业信息，想要将它们合并为“姓名-职业”的格式，可以使用CONCATENATE函数。

假设A1单元格中为“张三”，B1单元格中为“教师”，则在C1单元格中输入以下公式：=CONCATENATE(A1, "-", B1)按下回车键后，C1单元格将显示为“张三-教师”。

二、利用IF函数实现条件文本合并IF函数是Excel中常用的逻辑函数，它用于根据条件判断返回不同的结果。

结合CONCATENATE函数，我们可以实现带条件的文本合并。

IF函数的基本语法为：=IF(logical_test, value_if_true, value_if_false)其中，logical_test为需要进行判断的逻辑表达式，value_if_true为满足条件时返回的结果，value_if_false为不满足条件时返回的结果。

举个例子，假设我们有一个学生成绩表格，A列为学生姓名，B列为语文成绩，C列为数学成绩。

现在我们要根据学生的成绩情况，生成简要的评价信息，即如果语文和数学成绩均大于80，则显示为“优秀”，否则显示为“一般”。

可以在D1单元格中输入以下公式：=IF(AND(B1>80,C1>80),"优秀","一般")根据具体情况调整单元格的引用范围，然后拖动填充手柄将公式应用到其它单元格。

在逻辑函数的表示方法中，逻辑表达式是一种常用的方式。

逻辑表达式是由逻辑变量和逻辑运算符组成的表达式，用来描述逻辑函数的行为。

逻辑表达式的形式简单直观，易于理解和分析，因此在逻辑设计和分析中被广泛应用。

让我们来了解一下什么是逻辑函数。

逻辑函数是一种将逻辑变量映射为逻辑值的函数。

在数字电路中，逻辑函数通常用来描述输入和输出之间的逻辑关系，例如布尔运算、逻辑门的运算等。

逻辑函数可以用真值表或逻辑表达式来表示，而逻辑表达式正是一种常用的表示方法。

在逻辑表达式中，我们通常会用到逻辑变量和逻辑运算符。

逻辑变量可以取值为0或1，用来表示逻辑条件的真假。

而逻辑运算符包括与、或、非、异或等，用来表示逻辑变量之间的逻辑关系。

通过组合使用逻辑变量和逻辑运算符，我们可以构建出描述逻辑函数行为的逻辑表达式。

举个例子来说明，假设我们有两个逻辑变量A和B，它们分别表示两个逻辑条件，我们可以使用逻辑运算符与（AND）来描述它们的逻辑关系。

如果我们想要表示当A为真且B为假时，一个输出变量C为真，我们可以使用逻辑表达式C = A AND (NOT B) 来描述这种逻辑关系。

通过这个简单的例子，我们可以看到逻辑表达式的直观和简明特点。

逻辑表达式的形式简单，易于理解和分析，因此在逻辑设计和分析中被广泛应用。

在数字电路的设计中，我们经常会用到逻辑表达式来描述逻辑功能和行为，从而方便进行逻辑分析和优化。

而在计算机科学中，逻辑表达式也是描述逻辑关系和条件判断的重要工具，例如在编程语言中使用逻辑表达式来实现条件判断和逻辑运算。

逻辑表达式作为逻辑函数常用的表示方法，具有直观、简明、易于理解和分析的特点，在逻辑设计、数字电路、计算机科学等领域中发挥着重要作用。

通过深入学习和应用逻辑表达式，我们可以更好地理解和分析逻辑函数的行为，从而提高逻辑设计和分析的效率和质量。

逻辑表达式作为一种重要的逻辑表示方法，不仅对于专业人士，在日常生活中也有着重要的应用，希望通过本文对逻辑表达式的介绍，能够帮助读者更好地理解和应用这一重要概念。