中南大学matlab题目

大学matlab考试题及答案大学MATLAB考试题及答案一、选择题1. MATLAB的全称是什么？A. Matrix LaboratoryB. Microprocessor Application Tool SetC. Microsoft Advanced Tool SetD. Microprocessor Application Test System答案：A2. 在MATLAB中，以下哪个命令用于绘制三维图形？A. plotB. scatterC. surfD. bar答案：C3. MATLAB中用于求解线性方程组的函数是？A. solveB. linsolveC. linprogD. fsolve答案：A二、简答题1. 简述MATLAB的基本数据类型有哪些，并给出至少两个每种类型的示例。

答案：MATLAB的基本数据类型包括数值数组、字符数组和单元数组。

数值数组可以是向量、矩阵或多维数组。

例如，向量 `v = [1 2 3]`，矩阵 `M = [1 2; 3 4]`。

字符数组是由单引号或双引号括起来的字符序列，如 `C = 'Hello'`。

单元数组可以包含不同类型的数据，如`{1, 'text', [1; 2; 3]}`。

2. 描述如何在MATLAB中实现矩阵的转置和翻转。

答案：矩阵的转置可以通过 `'T'` 来实现，例如 `A'` 表示矩阵A 的转置。

矩阵的翻转可以通过 `flip` 函数实现，例如 `flip(A)` 可以翻转矩阵A的所有行和列，`flipud(A)` 仅翻转矩阵A的行，而`fliplr(A)` 仅翻转矩阵A的列。

三、编程题1. 编写一个MATLAB函数，该函数接受一个向量作为输入，并返回向量中所有元素的和以及平均值。

```matlabfunction [sumVal, avgVal] = calculateSumAndAverage(V)sumVal = sum(V);avgVal = mean(V);end```2. 设计一个MATLAB脚本来解决以下问题：给定一个3x3的矩阵，找出其中最大的元素，并显示其位置。

的491操作题集操作题1 《Matlab与科学计算》P28 例2.1要求计算水在温度为0℃，20℃，40℃，60℃，80℃时的黏度，已知水的黏度随/(1+at+bt2)温度的变化公式为μ=μ为0℃水的黏度，值为1.758*10-3。

其中μ要求分别以长短格式显示计算结果。

操作题2 《Matlab与科学计算》P31 例2.2数值数组【1：5】和字符串转换示例。

操作题3《Matlab与科学计算》P44 例2.9比较用左除和右除法分别求解恰定方程的解。

操作题4 《Matlab与科学计算》 P48 例2.14计算矩阵magic(3)的指数，并比较不同函数的结果。

指数运算expm(a)操作题5 《Matlab与科学计算》 P50 例2.18计算下面矩阵[-149 -50 -154；537 180 546；-27 -9 -25]的特征值条件数。

特征值函数condeig(A)操作题6《Matlab与科学计算》P62 例2.29对矩阵a = 1 1 1 11 2 3 41 3 6 101 4 10 20 进行三角抽取使之分别变成0 0 0 0 1 1 1 01 0 0 0 及 123 41 3 0 0 1 3 6 101 4 10 0 1 4 10 20操作题7《Matlab与科学计算》P62 例2.30用3种方法建立向量v 为[1 2 6 20]多项式的伴随矩阵。

操作题8《Matlab与科学计算》P64 例2.31已知a=[2 1 -3 -1；3 1 0 7；-1 2 4 -2；1 0 -1 5]；求该矩阵的3次方及数组的3次方。

操作题9《Matlab与科学计算》P66 例2.32 数组逻辑运算演示。

已知a=[1:3；4：6；7：9]，b=[0 1 0；1 0 1；0 0 1]， x=5, y=ones （3）*5,求x<=a，ab=a&b，～b操作题10《Matlab与科学计算》P71 例2.41对多项式p =[2 -5 6 -1 9]求根，计算其在x=3的值，进行微分计算并写出其表达式。

matlab试题及答案# MATLAB试题及答案一、选择题1. MATLAB的基本数据单位是：A. 矩阵B. 向量C. 标量D. 数组答案：A2. 下列哪个命令可以用来绘制函数图形？A. `plot`B. `graph`C. `draw`D. `chart`答案：A3. MATLAB中，以下哪个是正确的矩阵转置操作？A. `transpose(A)`B. `A'`C. `A^T`D. `flip(A)`答案：B二、简答题1. 简述MATLAB中矩阵的基本操作。

答案：在MATLAB中，矩阵是最基本的数据结构，可以进行加、减、乘、除等基本运算。

矩阵的创建可以使用方括号`[]`，例如`A = [1 2;3 4]`。

矩阵的转置使用单引号`'`，例如`A'`。

矩阵的求逆使用`inv`函数，例如`inv(A)`。

2. MATLAB中如何实现循环结构？答案：MATLAB中实现循环结构主要有两种方式：`for`循环和`while`循环。

`for`循环用于已知迭代次数的情况，例如：```matlabfor i = 1:5disp(i);end````while`循环用于迭代次数未知的情况，例如：```matlabi = 1;while i <= 5disp(i);i = i + 1;end```三、计算题1. 给定矩阵A和B，请计算它们的乘积C，并求C的行列式。

A = [1 2; 3 4]B = [5 6; 7 8]答案：首先计算矩阵乘积C：```matlabC = A * B;```然后计算C的行列式：```matlabdetC = det(C);```结果为：```matlabC = [19 22; 43 50]detC = -16```2. 编写一个MATLAB函数，计算并返回一个向量的范数。

答案：```matlabfunction norm_value = vector_norm(v)norm_value = norm(v);end```四、编程题1. 编写一个MATLAB脚本，实现以下功能：- 随机生成一个3x3的矩阵。

中南大学matlab课后习题（10）Unit 1实验内容1.答：用help命令可以查询到自己的工作目录。

输入help命令：help <函数名>2.答：MATLAB的主要优点：通过例1-1至例1-4的验证，MATLAB的优点是MATLAB以矩阵作为数据操作的基本单位，使得矩阵运算变得非常简捷，方便，高效。

还提供了丰富的数值计算函数。

MATLAB绘图十分方便，只需输入绘图命令，MATLAB便可自动绘出图形。

3.答：INV(X) is the inverse of the square matrix X。

A warning message is printed if X is badly scaled or nearly singular. PLOT(X,Y) plots vector Y versus vector X. If X or Y is a matrix, then the vector is plotted versus the rows or columns of the matrix, whichever line up. If X is a scalar and Y is a vector, length(Y) disconnected points are plotted. PLOT(Y) plots the columns of Y versus their index. If Y is complex, PLOT(Y) is equivalent to PLOT(real(Y),imag(Y)).In all other uses of PLOT, the imaginary part is ignored. For vectors, MAX(X) is the largest element in X. For matrices,MAX(X) is a row vector containing the maximum element from each column. For N-D arrays, MAX(X) operates along the first non-singleton dimension. [Y,I] = MAX(X) returns the indices of the maximum values in vector I. If the values along the first non-singleton dimension contain more than one maximal element, the index of the first one is returned. ROUND(X) rounds the elements of X to the nearest integers. MAX(X,Y) returns an array the same size as X and Y with the largest elements taken from X or Y. Either one can be a scalar。

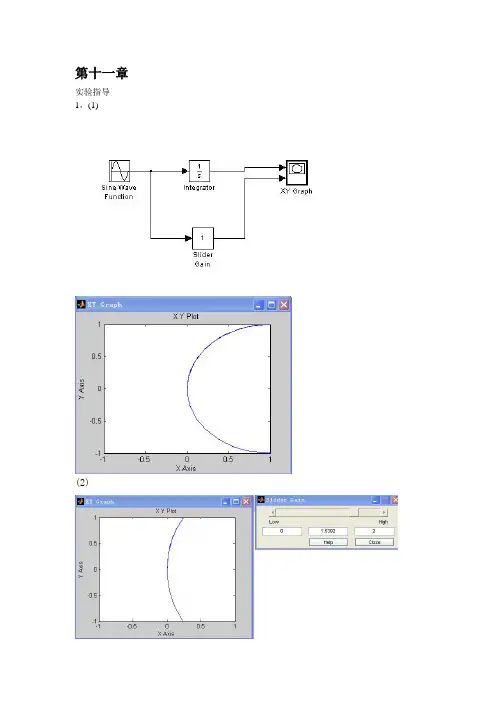
第十一章实验指导1，(1)(2)2，M文件的函数为：function x=f(t)x=(8*1/(pi^2))*(cos(2*pi*t)+(1/9)*cos(3*2*pi*t)+(1/25)*cos(5*2*pi*t))3,4,5,5，限幅：function [sys,x0,str,ts]=xianSfun(t,x,u,flag,max,min) switch flag,case 0sizes= simsizes;sizes.NumContStates = 0;sizes.NumDiscStates = 0;sizes.NumOutputs = 1;sizes.NumInputs = 1;sizes.DirFeedthrough = 1;sizes.NumSampleTimes = 1;sys= simsizes(sizes);str =[];x0 =[];ts =[-1 0];case 3if u>maxsys=max;elseif u<minsys=min;elsesys=u;endcase{1,2,4,9}sys=[];otherwiseerror(['Unhandled flag=',num2str(flag)]); end绝对值：function [sys,x0,str,ts]=abs(t,x,u,flag)switch flagcase 0sizes= simsizes;sizes.NumContStates = 0;sizes.NumDiscStates = 0;sizes.NumOutputs = 1;sizes.NumInputs = 1;sizes.DirFeedthrough = 1;sizes.NumSampleTimes = 1;sys= simsizes(sizes);str = [];x0 =[];ts =[0 0];case 3if u>0sys=u;else u<0sys=-u;endcase {1,2,4,9}sys=[];otherwiseerror(['Unhandled flag=',num2str(flag)]);end思考练习：1，两个主要功能Simu仿真和Link连接即该软件；天价模块——模块编辑——模块的连接——模块的参数和属性设置——设置仿真参数——启动系统仿真与仿真结果分析2，适用sinks模块库中的Scope模型或其他显示模块来观察有关信号的变化曲线，也可以将结果存放在MATLAB中的工作空间，工艺后处理和使用。

１求函数在指定点的导数值()232123,1,2,3 026x x xf x x x xx==>> syms x>＞ a=[x x^2 x^3；1 2*x ３*x^２;0 2 ６＊ｘ]; >＞ f＝deｔ(a);>> diff（f,1)ans =6＊x^2＞＞ diff(ｆ,2)ans =１2*x>> diff(f,3)aｎs ＝122 符号法求下列函数的导数或积分1）y＝ｘ１０+1０x+ｌogx1０,求y’f=（'x＾10＋10^x+log(1０）/log(x)'）f ＝x＾１0+10^ｘ+log(1０)/log(x)>> diff(f)ans ＝10*x^９+10＾x＊log（１0)-log(10)/ｌog(x）^2／x2）y=lｎ(１+ｘ), 求ｙ’’∣x=1f=(＇lｏg(1+x)／ｌｏg（e)＇)f =log(１+x）/ｌog(e)>> ｄiff(f，1,２)ans =-１／（1+x)^2/ｌog（ｅ）３) y=e x/ｃosx,求y’ｆ=(＇ｅxｐ(x)／ｃos(x）＇）f =exp(ｘ）/cos(x)>> diff（ｆ)ans =ｅｘp(x)/coｓ(x)+eｘp(x）/cos(x）^2*siｎ(x)４)functｉoｎｆ=fun0(t)f＝ｔ*sin(t)int('fｕn0','0'，'pｉ＇）aｎs =1／2*ｐi^2５) 已知函数z=ｓiｎ（xy), 计算sｙms x y>＞ｚ=('siｎ（x*y）'）z =ｓｉn(x*ｙ)>> difｆ(difｆ(z，ｙ,2)，ｘ)ans =-cos(ｘ*y)*y*ｘ^２－2*ｓin(x*y)＊ｘ3 用数值方法求定积分１）fｕncｔioｎｆ＝ｆuｎ(ｘ）f=x.^２.＊sqrｔ(２．*ｘ.^２+３）ｑuaｄ('fun＇，1,5)ａns ＝232.80572）fｕncｔion f=ｆｕn(x)f=ｘ．/ｓin（ｘ).^２quad(＇ｆun',pｉ/4,ｐi/３)ans =0.38354 已知数据［x,ｙ］如下表,试求２次拟合多项式f(x）,然后求x=0.0５，0.25,0.４５，０.6５，０．8５,1.０5各点的函数近似值，并绘出拟合曲线及求得的函数点。

大学专业试题-Matlab期末考试及答案一、选择题（每小题2分，共22分）1. 在matlab中____C____用于括住字符串。

A.，B.；C.‘’D.“”2. 在matlab的命令窗口中执行__A_______命令，可将命令窗口中所有变量清空。

A. clearB. clcC. echo offD. cd3.下列___D____是合法变量。

A. 1_1B. a/bC.变量1D. eps4产生所有元素均为1的2行3列矩阵的命令是_A______。

A. ones(2,3)B.ones(3,2)C.eye(2,3)D.eye(3,2)5．已知a=0:4,b=1:5,下面的运算表达式出错的是_D_______。

A. a+bB. a./bC. a.*bD. a*b6. subplot(2,1,2)是指__B_______的子图。

A.两行一列的上图B.两行一列的下图C.两列一行的左图D.两列一行的右图7.在多个句柄对象中，句柄是1的应该是_C_____对象。

A.根对象B.坐标轴C.窗口D.屏幕8.使用from:step:to方式生成向量，“-3：1：3”，其中-3，1，3分别是：（B）A、步长值，结束值，开始值B、开始值，步长值，结束值C、结束值，步长值，开始值D、开始值，结束值，步长值9.i=2; a=2i; b=2*i; c=2*sqrt(-1); 程序执行后a, b, c的值分别是多少？(C )A.a=4, b=4, c=2.0000iB.a=4, b=2.0000i, c=2.0000iC.a=2.0000i, b=4, c=2.0000iD.a=2.0000i, b=2.0000i, c=2.0000i10. 下列关于脚本文件和函数文件的描述中不正确的是(B )A. 去掉函数文件第一行的定义行可转变成脚本文件;B. 函数文件可以在命令窗口直接运行;C. 脚本文件可以调用函数文件;D. 函数文件中的第一行必须以function开始;11.下列对条件语句、分支语句、固定循环次数语句、不定循环次数语句关键字排序正确的是( B)A. if else end; for end; switch case end; while end;B. if else end; switch case end; for end; while end;C. for end; if else end; while end; switch case end;D. while end; for end; switch case end; if else end;二、填空题（20分，1空2分）1. 求可逆矩阵A的逆矩阵的指令是__inv(A) __.2. A=[0 2 3 0],B=[4 5 0 0],则X=A&B的显示结果为__ 0 1 0 0___.3. Matlab中用来表示不确定值的变量是_NaN_。

大学专业试题-Matlab期末考试及答案一、填空题（一题3分，共15分）1、标点符号可以使命令行不显示运算结果。

答案：%2、x为0〜4，步长为0.1pi的向量，使用命令创建。

答案：x=0:0.1*pi:4。

3、输入矩阵A=[1 2 3;7 -5 8;9-1-7],使用全下标方式用A（2,2）取出元素“-5 ”，使用单下标方式用取出元素“-5 ”。

答案：A （5）。

4、在while表达式,语句体,End循环语句中，表达式的值__时表示循环条件为真，体语句将被执行，否则跳出该循环语句。

答案：非零。

5、要从键盘读入一个字符串并赋值给变量x,且给出提示“Hello"，应使用命令—答案：x=input（‘Hello,；s'）b二、选择题（一题3分，共15分）1、下列表示可以作为MATLAB的变量的是(D )A. abcd-2B. xyz_2#C. @hD. X_1_a2、如果x=1: 2 : 8,则U x(1)和x(4)分别是(B )A. 1, 8B. 1,7C. 2,8D. 2,73、指出下列错误的指令（B）。

A.symsa b;B. symsa, b;C.syms('a',’b');D. syms('a','b','positive');4、下列哪条指令是求矩阵的行列式的值(C)。

A .inv B. diag C. det D.eig5、清空Matlab工作空间内所有变量的指令是(C)。

A. clcB.clsC.clearD. clf三、程序分析题（一题10分，共20分）1、分析下面程序运行后s1,n1,s2,n2,m的值。

s1=0;s2=0;n1=0;n2=0；x=[1,-4,-8,3,10,-9,7,-3,10, 8,-5,-2,2,0 ]; m=length(x); fori=1:mif x(i)<0s1=s1+x(i); n1=n1+1; elses2=s2+x(i); n2=n2+1;end ends1,n1,s2,n2,m请回答s1,n1,s2,n2,m的结果。

第一章思考练习1.与一般的Windows程序一样，启动MATLAB系统有3种常见方法：(1)使用Windows“开始”菜单。

(2)运行MATLAB系统启动程序matlab.exe。

(3) 利用快捷方式。

要退出MATLAB系统，也有3种常见方法：(2) 在MATLAB命令窗口输入Exit或Quit命令。

(3) 单击MATLAB主窗口的“关闭”按钮。

2.matlab用于算法开发、数据可视化、数据分析以及数值计算的高级技术计算语言和交互式环境，主要包括MATLAB和Simulink两大部分。

它将数值分析、矩阵计算、科学数据可视化以及非线性动态系统的建模和仿真等诸多强大功能集成在一个易于使用的视窗环境中，为科学研究、工程设计以及必须进行有效数值计算的众多科学领域提供了一种全面的解决方案3.可以在第一个物理行之后加上三个小黑点并按回车键，然后再下一个物理行输入其他部分。

4.help命令会显示当前帮助系统中的所有项目，即搜索路径中所有的目录名称，只显示那些与关键字中完全匹配的结果。

Lookfor命令对搜索范围内的M文件经行搜索，条件比较宽泛。

第二章（1） w=sqrt(2)*(1+0.34245*10^(-6)(2)a=3.5b=5c=9.8x=(2*pi*a+(b+c)/(pi+a*b*c)-exp(2))/(tan(b+c)+a)(3)a=3.32b=7.9y=2*pi*a^2*((1-pi/4)*b-(0.8333-pi/4)*a)(4) t=[2,1-3i;5,-0.65]Z=0.5*exp(2*t)*log(t+sqrt(1+t.*t))2. A=[-1,5,-4;0,7,8;3,61,7];B=[8,3,-1;2,5,3;-3,2,0];(1)A+6*B A^2-B+eye(2)A*B A.*B B.*A(3)A/B B\A(4)[A,B] [A([1,3],:);B^2]3.(1)A=[23,10,-0.778,0;41,-45,65,5;32,5,0,32;6,-9.54,54,3.14]; K=find(A>10&A<25);A(K)(2)A=[23,10,-0.778,0;41,-45,65,5;32,5,0,32;6,-9.54,54,3.14]; B=A(1:3,:) C=A(:,1:2) D=A(2:4,3:4) E=B*C(3)E<D E&D E|D ~E|~D5. A=[-29,6,18;20,5,12;-8,8,5];[V,D]=eig(A)A*V=V*D第三章1.f=input('输入一个数：','s');f(end :-1:1)2.(1)if语句score=input('请输入成绩:');if score>=90&&score<=100disp('A');elseif score>=80&&score<=89disp('B');elseif score>=70&&score<=79disp('C');elseif score>=60&&score<=69;disp('D');elseif score<60&&score>=0;disp('E');elsedisp('出错');End（2）用switch语句score=input('请输入成绩:');switch fix(score/10)case {9,10}disp('A');case {8}disp('B');case {7}disp('C');case {6}disp('D');case {0,1,2,3,4,5}disp('E');otherwisedisp('出错');End3.b=max(a)c=min(a)b=0c=0for i=1:20if a(i)>bb=a(i);endif a(i)<cc=a(i);End4.a=[-3:0.1:3];b=((exp(0.3.*a)-exp(-0.3.*a))./2)c=sin(a+0.3)for i=1:61y=(exp(0.3*a(i))-exp(-0.3*a(i)))/2*sin(a(i)+0.3)+log((0.3+a(i))/2) End5.（1）A=0;n=100for i=1:nA=1/n/n+A;End(2)A=1;n=10000;for i=1:nA=(2*n*n*2)/((2*n-1)*(2*n+1))*A;end6. A=rand(5,6)n=input('ÇëÊäÈëÒ»¸ön');if n>5n=5A(n,n)elseA(n)7.f1.m 代码:function m=f1(n)m=n+10*log(n^2+5);f2.m 代码:function m=f2(n)m=0;for i=1:nm=m+i*(i+1);end在命令文件p3_11.m 中调用f1.m 和f2.mp3_11.m 代码如下:y1=f1(40)/(f1(30)+f1(20));y2=f2(40)/(f2(30)+f2(20));y1y28.∑=1001k k 函数文件factor1.m 代码如下:function f=factor1(k)if k==1f=1;elsef=factor1(k-1)+k;end∑=5012^k k 函数文件factor2.m 代码:function f=factor2(k)if k==1f=1;elsef=factor2(k-1)+^2;end∑=101/1k k 函数文件factor3.m 代码:function f=factor3(k)if k==1f=1;elsef=factor3(k-1)+1/k;end思考练习2.N=[1,2,3,4,5]A=N.*2B=N./4C=1./ND=1./(N./2)./(N./2)/43.B=0for i=1:20A(i)=fix((99-10+1)*rand(1)+10);B=A(i)+B;endB=B/20for i=1:20if A(i)<B&rem(A(i),2)==0A(i)end第四章.1.(1).x=-12:0.001:12;y=x-x.^3/6;plot(x,y);xlabel('x 轴');ylabel('y 轴');title('Y=X-X^3/3!');(2)t=0:0.01:2*pi;x=8.*cos(t);y=4*sqrt(2).*sin(t);plot(x,y)2.t=-pi:pi/10:pi;y=1./(1+exp(-t));subplot(2,2,1);bar(t,y,'b');title('bar(t,y,''b'')');axis([-5,5,-3,3]); subplot(2,2,2);stairs(t,y,'k');title('stairs (t,y,''k'')');axis([-5,5,-3,3]); subplot(2,2,3);stem(t,y,'m');title('stem (t,y,''m'')');axis([-5,5,-3,3]); subplot(2,2,4);loglog(t,y,'g');title('loglog(t,y,''g'')');axis([-5,5,-3,3]);3.(1) t=0:pi/100:2*pi;y=5*cos(t)+4;polar(t,y,'-*')(2)t=-pi/3:pi/100:pi/3;r=5*sin(t).^2./cos(t);polar(t,r,'-*')4.(1)t=0:pi/100:2*pi;x=exp(-t/20).*cos(t);y=exp(-t/20).*sin(t);z=t;plot3(x,y,z)(2) [x,y]=meshgrid(-5:5);z=ones(11);surf(x,y,z);shading interp;5.[x,y,z]=sphere(50);m=moviein(100);for i=1:100surf(i*x,i*y,i*z);shading interpcolormap(hot);axis equalaxis([-100,100,-100,100,-100,100]) axis offm(:,i)=getframe;End思考练习2.（1）x=1:0.1:10a=exp((x.^2)/2)y=a.*1/2/piplot(x,y)（2）t=-pi:0.1:2*piX=t.*sin(t)Y=t.*cos(t)plot(X,Y)3.t=0:0.00005:pi;x=sin(3*t).*cos(t);y1=2*x-0.5;y2=sin(3*t).*sin(t);plot(x,y2,x,y1);hold onk=find(abs(y2-y1)<1e-4);x1=x(k);y3=2*x1-0.5;plot(x1,y3,'rp')4.x=-pi*6:0.1:pi*6y=sin(1./x)plot(x,y)fplot('sin(1./x)',[-pi*6,pi*6],1e-4)5.（1）x=1:0.1:10y=12./xpolar(x,y)(2)x=-pi/6:0.1:pi/6y=3*sin(x).*cos(x)./(sin(x).^3+cos(x).^3) polar(x,y)6.（1）[u,v]=meshgrid(-pi:pi/100:pi);x=3*u.*sin(v);y=2*u.*cos(v);z=4*u.*u;mesh(x,y,z);（2）[x,y]=meshgrid(-3:6/100:3);z=-5./(1+x.*x+y.*y);mesh(x,y,z)第五章1.A=randn(10,5)(1) X=mean(A)Y=std(A,0,1)(2) max(max(A))min(min(A))(3) B=sum(A,2)sum(B)(4) sort(A);sort(A,2,'descend')2.(1)t=0:15:90;x1=[0,0.2588,0.5000,0.7071,0.8660,0.9659,1.0000];a1=0:1:90;y1=interp1(t,x1,a1,'spline')x2=[0,0.2679,0.5774,1.0000,1.7320,3.7320,NaN]; a2=0:1:75;y2= interp1(t,x2,a2,'spline')p1=polyfit(t,x1,5);Z1=polyval(p1,a1)p2=polyfit(t,x2,5);z2=polyval(p2,a2)(2)X=[1 4 9 16 25 36 49 64 81 100];Y=1:10;X1=1:100;Y1=interp1(X,Y,X1,'cubic')3.4.P=[2,-3,5,13];Q=[1,5,8];p=polyder(P)p1=polyder(P,Q)[p,q]= polyder(P,Q)5.P1=[1,2,4,0,5];P2=[1,0];P3=[1,2,3];1) P4=conv(P2,P3)P4=[0,1,2,3,0];P=P1+P42) x=roots(P)3) A=[-1,1.2,-1.4;0.75,2,3.5;0,5,2.5];Y=polyval(P,A)4)Z=polyvalm(P,A)第六章1.（1）>> A=[1/2,1/3,1/4;1/3,1/4,1/5;1/4,1/5,1/6];B=[0.95,0.67,0.52]';x=A\B （2）>> A=[1/2,1/3,1/4;1/3,1/4,1/5;1/4,1/5,1/6];B=[0.95,0.67,0.53]';x=A\B （3）>> cond(A)2.（1）建立函数文件funx.m，命令如下;Function fx=funx(x)fx=x^41+x^3+1;调用fzero函数求根，命令如下;>> z=fzero(@funx,-1)(2) 建立函数文件sin.m，命令如下;Function fx=sin(x)fx=x-(sin(x))/x;调用fzero函数求根，命令如下;>> z=fzero(@sin,0.5)(3) 建立函数文件myfun.m，命令如下;function q=myfun(p)x=p(1);y=p(2);z=p(3);q(1)=sin(x)+y^2+log(z)-7;q(2)=3*x+2^y-z^3+1;q(3)=x+y+z-5;调用fsolve函数求根，命令如下;>> options=optimset('Display','off');x=fsolve(@myfun,[1,1,1]',options)3.(1) 建立函数文件funt.m,命令如下;function yp=funt(t,y)yp=-y*(1.2+sin(10*t));求微分方程，程序如下：>> t0=0;tf=5;y0=1;[t,y]=ode23(@funt,[t0,tf],y0)(2) 建立函数文件funr.m,命令如下;function yp=funr(t,y)yp=cos(t)-(y)/(1+t^2);求微分方程，程序如下：>> t0=0;tf=5;y0=1;[t,y]=ode23(@funr,[t0,tf],y0)4.建立函数文件mymax.m命令如下:function fx=mymax(x)fx=-1*(1+x^2)/(1+x^4);求最大值，程序如下:>> [x,y]=fminbnd(@mymax,0,2)5.编写目标函数M文件fop.m，命令如下:function f=fop(x)f=-1*(x(1)^(1/2)+x(2)^(1/2)+x(3)^(1/2)+x(4)^(1/2)); 设定约束条件，并调用fmincon函数求解此约束最优化问题，程序如下：>>x0=[200,200,200,200];A=[1,0,0,0;1.21,1,0,0;1.331,1.21,1,0;1.4641,1.331,1.21,1];b=[400,440,484,532.4];Ib=[0,0,0,0];options=optimset('Display','off');[x,y]=fmincon(@fop,x0,A,b,[],[],Ib,[],[],options)思考练习1,(1)矩阵求逆：>> A=[2,3,5;3,7,4;1,-7,1];b=[10,3,5]';x=inv(A)*b矩阵除法：>> A=[2,3,5;3,7,4;1,-7,1];b=[10,3,5]';x=A\b矩阵分解：>> A=[2,3,5;3,7,4;1,-7,1];b=[10,3,5]';[L,U]=lu(A);x=U\(L\b)(2)矩阵求逆：>> A=[6,5,-2,5;9,-1,4,-1;3,4,2,-2;3,-9,0,2];b=[-4,13,1,11]';x=inv(A)*b矩阵除法：>> A=[6,5,-2,5;9,-1,4,-1;3,4,2,-2;3,-9,0,2];b=[-4,13,1,11]';x=A\b矩阵分解：>> A=[6,5,-2,5;9,-1,4,-1;3,4,2,-2;3,-9,0,2];b=[-4,13,1,11]'; [L,U]=lu(A);x=U\(L\b)2.(1)建立函数文件fun1.m，命令如下：function fx=fun1(x)fx=3*x+sin(x)-exp(x);调用fzero函数求根，命令如下;>> y=fzero(@fun1,1.5)(2) 建立函数文件fun2.m，命令如下：function fx=fun2(x)fx=1-(1/x)+5;调用fzero函数求根，命令如下;>> y=fzero(@fun2,1)(3) 建立函数文件myfun3.m，命令如下;function q=fun3(p)x=p(1);y=p(2);q(1)=x^2+y^2-9;q(2)=x+y-1;调用fsolve函数求根，命令如下;>> options=optimset('Display','off');x=fsolve(@fun3,[1,1]',options)3.(1)建立函数文件fun5.m，命令如下：function ydot=fun5(t,y)ydot(1)=(2-3*y(2)-2*t*y(1))/(1+t^2);ydot(2)=y(1);ydot=ydot';求解微分方程，命令如下：>> t0=0;tf=5;x0=[0,1];[t,y]=ode45(@fun5,[t0,tf],x0);[t,y](2) (1)建立函数文件fun5.m，命令如下：function ydot=fun6(t,y)ydot(1)=cos(t)+(5*y(1)*cos(2*t))/(t+1)^2-y(2)-y(3)/(3+sin(t)); ydot(2)=y(1);ydot(3)=y(2);ydot=ydot';求解微分方程，命令如下：>> t0=0;tf=5;x0=[0,1];[t,y]=ode45(@fun5,[t0,tf],x0);[t,y]4.建立函数文件max.m命令如下:function fx=max(x)fx=-1*(sin(x)+cos(x^2));求最大值，程序如下:>> [x,y]=fminbnd(@mymax,0,pi)5.编写目标函数M文件fop.m，命令如下:function f=topm(x)f=-1*x*(3-2*x)^2;设定约束条件，并调用fmincon函数求解此约束最优化问题，程序如下：>>x0=[0];A=[1];b=[1.5];Ib=[0];options=optimset('Display','off');[x,y]=fmincon(@top,x0,A,b, [],[],Ib,[],[],options)第七章1．function f=f1(x)f=sin(x)./x;function f=f2(x)f=[1./((x-0.3).^2+0.01)-1./((x-0.9).^2+0.04)-6];[I,n]=quad(@f1,0,2)[S,n]=quad(@f2,0,1)2．f=inline('exp(-x.^2-y.^2)','x','y');I1=dblquad(f,0,1,0,1)f=inline('abs(cos(x+y))','x','y');I2=dblquad(f,0,pi,0,pi)3. X=0.3:0.2:1.5;Y=[0.3895,0.6598,0.9147,1.1611,1.3971,1.6212,1.8325];trapz(X,Y)4. x=0:pi/5:2*pi;for n=1:3nDX=diff(sin(x),n)end5. f=inline('sin(x)./(x+cos(2.*x))');g=inline('[cos(x).*(x+cos(2.*x))-sin(x).*(1-2.*sin(2.*x))]./(x+cos(2.*x)).^2');x=0:0.01:2*pi;p=polyfit(x,f(x),5);dp=polyder(p);dpx=polyval(dp,x);dx=diff(f([x,2*pi+0.01]))/0.01;gx=g(x);plot(x,dpx,x,dx,'-',x,gx,':')思考练习1.求解定积分的数值方法有梯形法、辛普森法、高斯法等，基本思想是将整个积分区间分成n个子区间，而每个小的子区间上的定积分的值可近似求得。