矩形的性质与判定 2

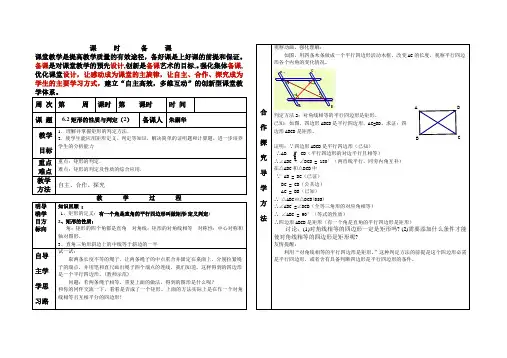
矩形的定义性质与判定
1．矩形的定义：有一个角是直角的平行四边形叫做矩形．
2．矩形的性质
矩形是特殊的平行四边形，它具有平行四边形的所有性质，•还具有自己独特的性质：
①边的性质：对边平行且相等．
②角的性质：四个角都是直角．
③对角线性质：对角线互相平分且相等．
④对称性：矩形是中心对称图形，也是轴对称图形．
直角三角形斜边上的中线等于斜边的一半．
直角三角形中，30°角所对的直角边等于斜边的一半．
3．矩形的判定
判定①：有一个角是直角的平行四边形是矩形．
判定②：对角线相等的平行四边形是矩形．
判定③：有三个角是直角的四边形是矩形．。

1．什么叫做平行四边形？什么叫做矩形？2．矩形有哪些性质？3．矩形与平行四边形有什么共同之处？有什么不同之处？4．事例引入：小华想要做一个矩形像框送给妈妈做生日礼物，于是找来两根长度相等的短木条和两根长度相等的长木条制作，你有什么办法可以检测他做的是矩形像框吗？看看谁的方法可行？1、自主学习：矩形是特殊的平行四边形，怎样判定一个平行四边形是矩形呢?请同学们说出最基本的方法：（用定义）2、合作探究：知识点一：探究“对角线相等的平行四边形是矩形。

”如图在□ABCD中，对角线AC、BD相交于O，如果AC=BD求证：□ABCD是矩形。

知识点二：探究“三个角都是直角的四边形是矩形。

”已知：在四边形ABCD中∠A=∠B=∠C=90︒求证：四边形ABCD矩形【典例分析】已知平行四边形ABCD的对角线AC、BD相交于点O，△AOB是等边三角形，AB=4 cm，求这个平行四边形的面积．1、下列各句判定矩形的说法是否正确？为什么？（1）有一个角是直角的四边形是矩形；（2）有四个角是直角的四边形是矩形；（3）四个角都相等的四边形是矩形；（4）对角线相等的四边形是矩形；（5）对角线相等且互相垂直的四边形是矩形；（6）对角线互相平分且相等的四边形是矩形；（7）对角线相等，且有一个角是直角的四边形是矩形；（8）一组邻边垂直，一组对边平行且相等的四边形是矩形；（9）两组对边分别平行，且对角线相等的四边形是矩形．指出：（l）所给四边形添加的条件不满足三个的肯定不是矩形；（2）所给四边形添加的条件是三个独立条件，但若与判定方法不同，则需要利用定义和判定方法证明或举反例，才能下结论．2、如图，□ABCD中，AB= 6，BC= 8，AC= 10 ，求证: □ABCD是矩形。

3、如上图已知：□ABCD的AC、BD对角线相交于O，△AOB是等边三角形，AB=4cm,求这个平行四边形的面积。

【课后作业】必做题：习题1.5选做题：△ABC中，点O是AC边上一动点，过O点作直线MN//BC，设MN交∠BCA的平分线于点E，交∠BCA的外角平分线于点F，（1）试说明EO=OF的理由。

第一章特别平行四边形2.矩形的性质与判断 ( 二 )一、学生知识情况剖析学生在初二平行四边形一章中，已经认识了三种特别平行四边形矩形、菱形和正方形，同时，经过平行四边形和菱形的学习，进行了对平行四边形和菱形性质和判断的证明，学生已经有了必定的推理论证能力，掌握了独立证明特别平行四边形性质及判断定理的基本技术；在有关知识的学习中，学生已经经历了大批的证明活动，特别是平行四边形的有关证明推理，学生已经渐渐领会到了证明的必需性和证明在解决实质问题时的作用，进而初步具备了证明特别平行四边形性质和判断定理的能力；同时，在前面的有关活动中，学生已经初步认识了归纳、归纳及转变等数学思想方法，大批的活动经验丰富了学生的数学思想，锻炼了学生的能力，使学生具备了在解题中合理运用方法的能力。

二、教课任务剖析课本鉴于当前学生的知识和能力水平，对本课内容提出了详细的学习任务：进一步发展推理论证能力，运用综合法证明矩形的性质和判断定理，进一步领会证明的必需性和作用，领会归纳等数学思想方法。

关于本节课的知识，教科书提出的学习任务，要点集中在了学生的能力培育上，在教课时，我们应当把目标上涨一个层次，从关注学生能否能证明这些定理提升到关注学生如何找到解题思路，从关注学生能否能顺利证明提升到关注学生能否合理严实的使用数学语言严格证明，从关注学生合作解题提升到让每一个学生都能独立达成证明的过程。

能力培育不单是本节课教课过程中的近期目标，更是为此后学生学习数学知识打下基础的远景目标，能力的培育也必定带动学生感情态度目标的达成。

同时，在教课中，还一定注意对不一样层次的学生拟订不一样的教课任务，做到让每一个学生都能在讲堂上有所收获。

为此，本节课我们要达到的详细教课目的为：1．能够运用综合法和严实的数学语言证明矩形的性质和判断定理以及其余有关结论；2．经历探究、猜想、证明的过程，发展学生的推理论证能力，培育学生找到解题思路的能力，使学生进一步领会证明的必需性以及计算与证明在解决问题中的作用；3．学生经过对照前面所学知识，领会证明过程中所运用的归纳、归纳以及转变等数学思想方法；4．经过学生独立达成证明的过程，让学生领会数学是谨慎的科学，加强学生对待科学的谨慎治学态度，进而养成优秀的习惯。

二、再探新知
1、什么样的四边形是矩形？
由定义得到矩形的第一个判定方法。

2、回顾上节课的活动：在一个平行四边形活动框架上，用两根像皮筋分别套在相对的两个顶点上，拉动一对不相邻的顶点，改变平行四边形的形状，当对角线满足什
么条件时，平行四边形就成为矩形？
对角线相等的平行四边形是矩形.
如图，在ABCD中，AB=CD，BD=AC，BC=BC.
∴△ABC≌△DCB(SSS)
∴∠ABC=∠DCB.
在ABCD中，AB∥CD，
∴∠ABC+∠DCB=180°
∴2∠ABC=180°，即∠ABC=90°
∴ABCD是矩形.
∴对角线相等的平行四边形是矩形. 观察、发现、
交流，总
结出结
论。

证明此结
论。

学生先
思考，然后
说明证明过
程。

讨矩形的判定
方法。

再次让学生体
会定义的双重
性质。

第二讲矩形的性质与判定（一）矩形的定义与性质1.矩形的定义:有一角是直角的平行四边形叫做矩形.2.矩形的性质:（1）矩形的四个角都是直角（2）矩形的对角线相等（3）矩形既是中心对称图形，也是轴对称图形（4）矩形的面积计算：①矩形的面积等于长乘宽②矩形的面积等于被对角线分成的四个等积的小三角形面积之和。

3.矩形具有平行四边形的所有性质,应用矩形的性质可以进行计算和推理.典例分析：知识点1：利用矩形的性质求线段长例1：如图矩形ABCD的对角线AC、BD相交于O，已知∠AOD=120°，AB=4，求矩形ABCD 的面积．知识点2：利用矩形的性质求角的度数例2：如图，在矩形ABCD中，AE⊥BD，∠DAE：∠BAE=3：1，求∠BAE和∠EAO的度数．知识点3：利用矩形的性质证明例3：如图，四边形ABCD是矩形，△PBC和△QCD都是等边三角形，且点P在矩形上方，点Q在矩形内．求证：:（1）∠PBA=∠PCQ=30°；（2）PA=PQ．知识点4：利用矩形的对称性求面积例4：如图，EF过矩形ABCD对角线的交点O，且分别交AD、BC于点E、F已知AB=3，BC=4，则图中阴影部分的面积是（）A．3 B．4 C．6 D．12知识点5：:利用矩形的性质解决矩形中的折叠问题例5：（1）如图，在矩形ABCD中，AB=4，BC=6，点E为BC的中点，将△ABE沿AE折叠，使点B落在矩形内点F处，连接CF，则CF的长为．例5（1）图例5（2）图（2）如图，将长为12cm，宽6cm的矩形纸片ABCD折叠，使点A与点C重合，则折痕EF 的长为cm．（二）直角三角形的性质定理定理直角三角形斜边上的中线等于斜边的一半.典例分析：知识点6：利用直角三角形斜边上的中线的性质求线段长例6：如图，菱形ABCD的对角线AC，BD相交于点O，H为边AD的中点，若AC=6，BD=8，则OH的长等于．知识点7：利用直角三角形斜边上的中线的性质证明例7：如图，在四边形ABCD中，∠DAB=∠DCB=90°，对角线AC与BD相交于点O，M、N 分别是边BD、AC的中点．（1）求证：MN⊥AC；（2）当AC=8cm，BD=10cm时，求MN的长．（三）矩形的判定1.矩形的判定方法(1)有一个角是直角的平行四边形是矩形.(2)对角线相等的平行四边形是矩形.(3)有三个角是直角的四边形是矩形.2.判定一个四边形是矩形的方法与思路是:典例分析：知识点8：利用定义判定矩形例8：如图，在▱ABCD中，E、F分别是AB、DC边上的点，且AE=CF，（1）求证：△ADE≌△CBF．（2）若∠DEB=90°，求证：四边形DEBF是矩形．知识点9：利用“对角线相等的平行四边形是矩形”判定矩形例9：如图，在梯形ABCD中，E、F两点分别在边BC上．DE∥AB，AF∥DC，且四边形AEFD是平行四边形．（1）请判断线段AD与BC有何数量关系？并说明理由．（2）当AB=DC时．请猜想四边形AEFD是什么特殊的平行四边形？并说明理由．知识点10：利用“有三个角是直角的四边形是矩形”判定矩形例10：（1）如图，平行四边形ABCD的四个内角的平分线分别相交于点E、F、G、H，求证：四边形EFGH是矩形．（2）如图所示,在ΔABC中,AB＝AC,AD是ΔABC的一条角平分线,AN为ΔABC的外角∠CAM的平分线,CE⊥AN,垂足为E.求证:四边形ADCE是矩形.（四）矩形的性质与判定的综合应用例11：如图，矩形ABCD中，AB=2，BC=5，E、F分别在边AD，BC上，且DE=BP=1．（1）判断△BEC的形状，并说明理由．（2）判断四边形EFPH是什么特殊四边形？并证明你的判断．例12：如图，在平行四边形ABCD中，对角线AC，BD相交于点O，若E，F是AC上两动点，分别从A，C两点以相同的速度向C、A运动，其速度为1cm/s．（1）当E与F不重合时，四边形DEBF是平行四边形吗？说明理由；（2）若BD=12cm，AC=16cm，当运动时间t为何值时，以D、E、B、F为顶点的四边形是矩形？例13：如图，将▱ABCD的边AB延长到点E，使BE=AB，连接DE，交边BC于点F．（1）求证：△BEF≌△CDF；（2）连接BD、CE，若∠BFD=2∠A，求证：四边形BECD是矩形．夯实基础：1.矩形具有而平行四边形不一定具有的性质是（）A．对角线互相垂直 B．对角线相等C．对角线互相平分 D．对角相等2.若矩形的一条角平分线分一边为3cm和5cm两部分，则矩形的周长为（）A．22 B．26 C．22或26 D．283.如图，P是矩形ABCD的对角线AC的中点，E是AD的中点．若AB=6，AD=8，则四边形ABPE的周长为（）A．14 B．16 C．17 D．18第3题第4题第5题4.如图，矩形ABCD的对角线AC与BD相交于点O，CE∥BD，DE∥AC，AD=2，DE=2，则四边形OCED的面积（）A．2B．4 C．4D．85.如图，在矩形ABCD中（AD＞AB），点E是BC上一点，且DE=DA，AF⊥DE，垂足为点F，在下列结论中，不一定正确的是（）A．AF=AD B．AB=AF C．△AFD≌△DCE D．BE=AD﹣DF6.如图，矩形ABCD的两条对角线相交于点O，∠AOB=60°，AB=1，则矩形的面积等于．第6题第7题第8题7.如图，在矩形ABCD中，对角线AC、BD相交于点O，点E、F分别是AO、AD 的中点，若AB=6cm，BC=8cm，则EF=cm．8.如图，矩形ABCD中，对角线AC、BD交于点O，点E是BC上一点，且AB=BE，∠1=15°，则∠2=．9.如图，在Rt△ABC中，∠C=90°，BC=3，AC=4，M为斜边AB上一动点，过M 作MD⊥AC，过M作ME⊥CB于点E，则线段DE的最小值为．第9题第10题10.如图，在平面直角坐标系中，O为坐标原点，矩形OABC中，A（10，0），C （0，4），D为OA的中点，P为BC边上一点．若△POD为等腰三角形，则所有满足条件的点P的坐标为．11.如图，将长方形ABCD沿BD对折，点A落在点E处，BE与CD相交于点F，若AD=3，BF=5．（1）求证：△DEF≌△BCF；（2）求重叠部分的面积．12.如图，在矩形ABCD中，E、F分别是边AB、CD上的点，AE=CF，连接EF、BF，EF与对角线AC交于点O，且BE=BF，∠BEF=2∠BAC．（1）求证：OE=OF；（2）若BC=2，求AB的长．13.如图，四边形ABCD为平行四边形纸片．把纸片ABCD折叠，使点B恰好落在CD边上，折痕为AF．且AB=10cm、AD=8cm、DE=6cm．（1）求证：平行四边形ABCD是矩形；（2）求BF的长；（3）求折痕AF长．14.如图，△ABC中，BD、CE是△ABC的两条高，点F、M分别是DE、BC的中点．求证：FM⊥DE．15.已知：如图，△ABC中，O是AC边上一个动点，过点O作直线MN∥BC，设MN交∠BCA的平分线于点E，交∠BCA的外角平分线于点F．（1）求证：EO=FO；（2）写出当点O运动到何处时，四边形AECF是矩形；（3）当点O运动到问题（2）中的位置时，证明四边形AECF是矩形．。

矩形的性质与判定（2）研学案第一环节：创设情境，提出问题活动内容：课前准备小木板和橡皮筋，制作一个如图所示的平行四边形的活动框架。

在一个平行四边形活动框架上，用两根橡皮筋分别套在两个相对的顶点上，拉动一对不相邻的顶点时，平行四边形的形状会发生什么变化？第二环节：先猜想再实践，发展几何直觉活动内容：根据上面的实践活动提出以下两个问题：∠的变化，两条对角线将发生怎样的变化?（1）随着α（2）当两条对角线相等时，平行四边形有什么特征？由此你能得到一个怎样的猜想?学生在小组中完成这个活动的过程中，会引发对于这两个问题的讨论，请学生根据实践的结果对问题进行回答，再对比前面所学的平行四边形及菱形的判定定理的证明过程，来思考如何证明矩形的判定定理。

然后通过小组合作，将定理的证明严格的完成，最后同学实物投影的形式，各小组之间进行交流。

对比前一节学习的菱形和矩形的性质定理，引导学生对矩形独有的第一个判定定理进行证明：教师板书本题证明过程。

定理两条对角线相等的平行四边形是矩形。

（1）学生独立画出图形，在教师引导下写出已知、求证；（2）对比平行四边形和菱形的判定定理的证明，对已知、求证进行分析；（3）请学生交流大体思路；（4）用规范的数学语言写出证明过程；（5）同学之间进行交流，找出自己还存在的问题。

第三环节：再创情境，猜想实践活动内容：教师给出PPT中的情境二：李芳同学用四步画出一个四边形，“边、直角、边----直角、边----直角、边”，她说这就是一个矩形，她说的对吗？为什么？学生现猜想然后小组讨论，将讨论的结果进行证明。

定理三个角是直角的四边形是矩形。

（1）学生独立画出图形，在教师引导下写出已知、求证；（2）对比平行四边形和菱形的判定定理的证明，对已知、求证进行分析；（3）请学生交流大体思路；（4）用规范的数学语言写出证明过程；（5）同学之间进行交流，找出自己还存在的问题。

第四环节：实际应用，范例教学；活动内容：1．教师实际问题：①如果仅有一根足够长的绳子，如何判断一个四边形是平行四边形？②如果仅有一根足够长的绳子，如何判断一个四边形是菱形？③如果仅有一根足够长的绳子，如何判断一个四边形是矩形？请说明如何操作，并说明这样做的原因。

第一章特殊平行四边形1.2 矩形的性质与判定2【课程标准要求】理解特殊矩形的概念，探索并证明矩形的性质定理以及它的判定定理【教材分析】课本基于目前学生的知识和能力水平，对本课内容提出了具体的学习任务：进一步发展推理论证能力，运用综合法证明矩形的性质和判定定理，进一步体会证明的必要性和作用，体会归纳等数学思想方法。

对于本节课的知识，教科书提出的学习任务，重点集中在了学生的能力培养上，在教学时，我们应该把目标上升一个层次，从关注学生是否能证明这些定理提高到关注学生如何找到解题思路，从关注学生是否能顺利证明提高到关注学生是否合理严密的使用数学语言严格证明，从关注学生合作解题提高到让每一个学生都能独立完成证明的过程。

能力培养不仅是本节课教学过程中的近期目标，更是为今后学生学习数学知识打下基础的远景目标，能力的培养也必然带动学生情感态度目标的达成。

同时，在教学中，还必须注意对不同层次的学生制定不同的教学任务，做到让每一个学生都能在课堂上有所收获。

【学情分析】学生在初二平行四边形一章中，已经认识了三种特殊平行四边形矩形、菱形和正方形，同时，通过平行四边形和菱形的学习，进行了对平行四边形和菱形性质和判定的证明，学生已经有了一定的推理论证能力，掌握了独立证明特殊平行四边形性质及判定定理的基本技能；在相关知识的学习中，学生已经经历了大量的证明活动，特别是平行四边形的相关证明推理，学生已经逐渐体会到了证明的必要性和证明在解决实际问题时的作用，从而初步具备了证明特殊平行四边形性质和判定定理的能力；同时，在前面的相关活动中，学生已经初步了解了归纳、概括及转化等数学思想方法，大量的活动经验丰富了学生的数学思想，锻炼了学生的能力，使学生具备了在解题中合理运用方法的能力。

【教学目标：】知识与技能：理解矩形的判别条件及其证明，并能利用这两个定理解决一些简单的问题过程与方法：经历实际操作，探索矩形判定定理的证明过程，发展合情推理能力和初步的演绎推理的能力情感与态度：通过“实验—猜想—证明—应用“的数学活动提升科学素养【教学重点：】矩形的判别条件及其证明【教学难点：】矩形的判定定理的证明与简单应用【教学过程：】一、课前预习：阅读课本P14-15内容，并完成下列题目1、记住矩形的判定定理并尝试证明2、试做例题13、完成课后随堂练习二、课内检测1、四边形ABCD中，∠A =∠B =∠C =∠D, 则四边形ABCD是；2、下列命题是真命题的是（）；A.有一个角是直角的四边形是矩形B.两条对角线相等的四边形是矩形C.有三个角是直角的四边形是矩形D.对角线互相垂直的四边形是矩形3、矩形ABCD的对角线相交于点O，如果ABC∆的周长大10cm，则AD的长是∆的周长比AOB（）A、5cmB、7.5cmC、10cmD、12.5cm4、如果矩形的一边长为8，一条对角线长为10，那么这个矩形面积是__________。

第2讲 矩形的性质与判定 1. 理解矩形、概念和判定定理；2．灵活运用矩形、性质进行证明和计算． 知识点01 矩形的性质（1）矩形的定义：有一个角是直角的平行四边形是矩形．（2）矩形的性质①平行四边形的性质矩形都具有；②角：矩形的四个角都是直角；③边：邻边垂直；④对角线：矩形的对角线相等；⑤矩形是轴对称图形，又是中心对称图形．它有2条对称轴，分别是每组对边中点连线所在的直线；对称中心是两条对角线的交点．（3）由矩形的性质，可以得到直角三角形的一个重要性质，直角三角形斜边上的中线等于斜边的一半． 【知识拓展】例1.如图，已知矩形ABCD 中，E 是AD 上一点，F 是AB 上的一点，EF EC ⊥，且EF EC =．（1）求证：AEF DCE △≌△．（2）若5cm DE =，矩形ABCD 的周长为38cm ，求AE 的长．知识精讲目标导航知识点02 矩形的判定（1）矩形的判定：①矩形的定义：有一个角是直角的平行四边形是矩形；②有三个角是直角的四边形是矩形；③对角线相等的平行四边形是矩形（或“对角线互相平分且相等的四边形是矩形”）（2）①证明一个四边形是矩形，若题设条件与这个四边形的对角线有关，通常证这个四边形的对角线相等．②题设中出现多个直角或垂直时，常采用“三个角是直角的四边形是矩形”来判定矩形．【知识拓展】例2．已如，如图，在△ABC中，AB＝AC，AD是BC边的中线，过点A作BC的平行线，过点B 作AD的平行线，两线交于点E，连接DE交AB于点O．（1）求证：四边形ADBE是矩形；（2）若BC=8，AO=52，求四边形AEBC的面积．知识点03 矩形折叠问题【知识拓展】例3．如图，将矩形ABCD 沿对角线AC 翻折，点B 落在点F 处，FC 交AD 于E ．（1）求证：AFE CDE ≌；（2）若6AB =，8BC =，求图中阴影部分的面积．知识点04与矩形有关的面积问题【知识拓展】例4.[关注数学文化]数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线，则所容两长方形面积相等（如图1所示）”这一推论，他从这一推论出发，利用“出入相补”原理复原了《海岛算经》九题古证．（以上材料来源于《古证复原的原理》、《吴文俊与中国数学》和《古代世界数学泰斗刘徽》）（1）请根据如图1完成这个推论的证明过程，证明：S 矩形NFGD ＝()ADC ANF FGC S S S +△△△﹣，S 矩形EBMF ＝ABC S ﹣（ + ）．易知，ADC ABC S S △△＝， ＝ ， ＝ ．可得S 矩形NFGD ＝S 矩形EBMF（2）如图2，点P 是矩形ABCD 的对角线BD 上一点，过点P 作EF ∥BC 分别交AB ，CD 于点E 、F ，连接PA ，PC ．若PE ＝5，DF ＝4，求图中阴影部分的面积．知识点05直角三角形斜边上中线【知识拓展】例5.如图，在四边形ACBD 中，90ACB ∠=︒，AB AD =，E 是BD 中点，过点E 作//EF AD 交AB 于点F ，连接CF ．请写出关于边、角的两条正确结论（不包括已知条件）：①_________；②_________．1.如图所示，菱形PQRS 内接于矩形ABCD ，使得点P 、Q 、R 、S 分别为边AB 、BC 、CD 、DA 上的点．已知PB =15，BQ =20，PR =30，QS =40．求矩形ABCD 的周长．2.将矩形ABCD 的四个角向内折起，恰好拼成一个既无缝隙又无重叠的四边形EFGH ，若EH =3，EF =4，求AD AB的值．能力拓展题组A 基础过关练一、单选题1．（2021·广东肇庆市·九年级一模）如图，在矩形ABCD 中，点E 在CD 上，连接,45,1,AE BE DAE CBE AD ∠=∠=︒=、则ABE △的周长等于( )A ．6．B ．42C ．222+D ．322+2．（2021·河北保定市·九年级一模）如图，证明矩形的对角线相等，已知：四边形ABCD 是矩形．求证：AC BD =．以下是排乱了的证明过程：①∴AB CD =、ABC DCB ∠=∠．②∵BC CB =③∵四边形ABCD 是矩形④∴AC DB =⑤∴ABC DCB ∆∆≌．证明步骤正确的顺序是（ ）A ．③①②⑤④B ．②①③⑤④C ．③⑤②①④D ．②⑤①③④3．（2021·陕西西安市第三中学九年级期末）矩形具有而菱形不一定具有的性质是（ ） A ．中心对称图形 B ．对边分别相等 C ．对角线互相平分 D ．对角线相等4．（2021·重庆市育才中学九年级期末）下列命题是真命题的是（ ）A ．有一个角是直角的四边形是矩形B ．对角线互相平分且相等的四边形是矩形C ．一组对边平行且相等的四边形是矩形D ．对角线互相垂直平分的四边形是矩形5．（2021·广东广州市·九年级二模）直角三角形的斜边长为10，则斜边上的中线长为（ ）．A ．2B ．3C ．4D ．5分层提分二、填空题6．（2021·河南九年级专题练习）如图，点O 是矩形ABCD 的对角线AC 的中点，OM ∥AB 交AD 于点M ，若OM=2，BC=6，则OB 的长为______．7．（2021·江苏南京市·九年级二模）如图，矩形ABCD 中，6AB =，8AD =，顺次连接AB 、BC 、CD 、DA 的中点得到四边形EFGH ，那么四边形EFGH 的面积为____．三、解答题8．（2021·新兴县环城中学九年级期中）如图,在□ABCD 中,DE ⊥AB,BF ⊥CD,垂足分别为E,F.(1)求证:AE=CF.(2)求证:四边形BFDE 为矩形.9．（2021·河北唐山市·九年级期末）已知：如图，四边形ABCD是平行四边形，CE∥BD交AD的延长线于点E，CE=AC．（1）求证：四边形ABCD是矩形；（2）若AB=4，AD=3，求四边形BCED的周长．10．（2021·全国九年级专题练习）如图，四边形ABCD是矩形，过点D作DE∥AC，交BA的延长线于点E．求证：∠BDA =∠EDA．AC BD相交于点,O且11．（2021·福建福州市·福州十八中九年级二模）如图，菱形ABCD的对角线,DE AC AE BD．求证：四边形AODE是矩形．//,//题组B 能力提升练一、单选题1．（2021·黑龙江齐齐哈尔市·九年级三模）下列条件中能判断一个四边形是菱形的是（ ）A ．对角线互相平分且相等B ．对角线互相垂直且相等C ．对角线互相平分且垂直D ．对角线互相垂直且一条对角线平分一组对角2．（2021·辽宁大连市·九年级二模）如图，矩形ABCD 中，对角线AC ，BD 交于点O ，∠AOD ＝60°，AD ＝2，则矩形ABCD 的面积是（ ）A ．2B ．23C ．43D ．83．（2021·浙江杭州市·九年级其他模拟）已知，矩形ABCD 中，E 为AB 上一定点，F 为BC 上一动点，以EF 为一边作平行四边形EFGH ，点G ，H 分别在CD 和AD 上，若平行四边形EFGH 的面积不会随点F 的位置改变而改变，则应满足（ ）A ．4AD AE =B ．2=AD ABC ．2AB AE =D ．3AB AE =4．（2021·江苏南通市·九年级二模）如图1，四边形ABCD 中，//AB CD ，90B ∠=︒，AC AD =．动点Р从点B 出发，沿折线B A D C ---方向以a 单位/秒的速度匀速运动，在整个运动过程中，BCP 的面积S 与运动时间t （秒）的函数图象如图2所示，则四边形ABCD 的面积是（ ）A ．75B ．80C ．85D ．90二、填空题 5．（2021·江苏镇江市·炎黄外国语学校九年级月考）如图，矩形纸片ABCD 中，已知16AD =，折叠纸片使AB 边与对角线AC 重合，点B 落在点F 处，折痕为AE ，且6EF =，则AB 的长为__________．6．（2021·黑龙江佳木斯市·九年级三模）如图，在矩形ABCD 中，3AB =，4BC =，E 为BC 中点，F 为CD 上一动点，则AF EF +的最小值为______．7．（2021·宁夏银川市·九年级一模）如图，在平面直角坐标系中，O 为坐标原点，四边形OABC 是矩形，点A 、C 的坐标分别为A （10，0），C （0，4），M 是OA 的中点，点P 在BC 边上运动．当PO =PM 时，点P 的坐标为______．8．（2021·哈尔滨市第六十九中学校九年级三模）已知矩形ABCD ，点E 在AD 边上，DE AE >，连接BE ，将ABE △沿着BE 翻折得到BFE △，射线EF 交BC 于G ，若点G 为BC 的中点，1FG =，6DE =，则AE 的长______．9．（2021·浙江杭州市·九年级二模）如图，在矩形纸片ABCD 中，AB ＝1，点E 、F 分别是AB 和CD 的中点，H 为BC 上的一点，现将△ABH 沿AH 折叠，使点B 落在直线EF 上的点G ．当△ADG 为等腰三角形时，AD ＝_______．10．（2021·湖北孝感市·九年级二模）如图，将矩形纸片ABCD （AD AB >）折叠，使点C 刚好落在线段AD 上，且折痕分别与边BC ，AD 相交，设折叠后点C ，D 的对应点分别为点G ，H ，折痕分别与边BC ，AD 相交于点E ，F ．若3AB =，9BC =，则线段CE 的最大值与最小值的和是_____．11．（2021·安徽合肥市·九年级三模）如图，在Rt ABC 中，90ACB ∠=︒，O 为AB 的中点，点E 在BC 上，且CE AC =，15BAE ∠=︒，则COE ∠的大小为______．三、解答题12．（2021·贵州中考真题）如图，在矩形ABCD 中，点M 在DC 上，AM AB =，且BN AM ⊥，垂足为N ．（1）求证：ABN MAD ≌；（2）若2,4AD AN ==，求四边形BCMN 的面积．13．（2021·湖南长沙市·中考真题）如图，ABCD 的对角线AC ，BD 相交于点O ，OAB 是等边三角形，4AB =．（1）求证：ABCD 是矩形；（2）求AD 的长．14．（2021·山东滨州市·九年级其他模拟）如图，菱形ABCD 的对角线AC ，BD 相交于点O ，E 是AD的中点，点F ，G 在AB 上，EF AB ⊥，//OG EF ．（1）求证：四边形OEFG 是矩形；（2）若13AD =，5EF =，求OE 和BG 的长．题组C 培优拔尖练一、单选题1．（2021·安徽中考真题）如图，在菱形ABCD 中，2AB =，120A ∠=︒，过菱形ABCD 的对称中心O 分别作边AB ，BC 的垂线，交各边于点E ，F ，G ，H ，则四边形EFGH 的周长为（ ）A ．33+B ．223+C ．23+D ．13+2．（2021·山东济宁市·九年级二模）如图，在矩形ABCD 中，AD 2AB ，∠BAD 的平分线交BC 于点E ，DH ⊥AE 于点H ，连接BH 并延长交CD 于点F ，连接DE 交BF 于点O ，下列结论：①∠AED ＝∠CED ；②OE ＝OD ；③BH ＝HF ；④AB ＝HF ，其中正确的有（ ）A ．1个B ．2个C ．3个D ．4个3．（2021·广东深圳市·深圳中学九年级月考）如图，在矩形ABCD 中，2AB BC =，E 为CD 上一点，且AE AB =，M 为AE 的中点．下列结论：①DM DA =；②EB 平分AEC ∠；③ABE ADE S S =△△；④22BE AE EC =⋅．其中结论正确的个数是（ ）A ．1B ．2C ．3D ．4二、填空题 4．（2021·河北九年级专题练习）如图，Rt ABC ∆中，90ACB ∠=︒，斜边9AB =，D 为AB 的中点，F 为CD 上一点，且13CF CD =，过点B 作//BE DC 交AF 的延长线于点E ，则BE 的长为____．5．（2021·山东潍坊市·九年级二模）如图，在矩形ABCD 中，点E 是BC 上一点，将ABE △沿AE 折叠，点B 落在AD 上的点F 处；点M 是CD 上一点，将ADM △沿AM 折叠，点D 与点E 恰好重合；若1AB =，则DM 的长等于______．6．（2021·黑龙江九年级三模）如图，在矩形ABCD 中，6AB =，8BC =，对角线AC ，BD 相交于点O ，P 为边AD 上一动点，连接OP ．若AOP 为等腰三角形，则OP 的长为______．三、解答题7．（2021·黑龙江哈尔滨市·九年级一模）如图，△ABC 中，AB ＝AC ，M 为AD 中点，过点A 作AE ∥BC 交BM 延长线于点E ，连接CE ．（1）求证：四边形ADCE 为矩形；（2）连接DE 交AC 于点G ，连接MG ，在不添加辅助线的条件下请直接写出面积等于△ABM 面积一半的所有三角形．。