感生电动势

第九周学习内容第33讲感生电动势及感生电场第34讲感生电动势例题第35讲涡电流及电磁阻尼第36讲自感与互感第33讲 感生电动势及感生电场 第34讲 感生电 动势例题感生电动势：回路中单纯由磁场变化产生的感应电动势。

d ∂∂LSBEl St d ⋅=-⋅⎰⎰感生感LEli d ε=⋅⎰i SBSt t d d d Φε∂=-=-⋅∂⎰感生电场 ：产生感生电动势的非静电起源的作用力本质上是一种电场力。

感Ed d LSBE l St ⋅=-⋅⎰⎰感生∂∂d 0SE S ⋅=⎰感生感应电场为非保守场、无源场、涡旋场实际电场感生静电E E E +=d d LSBE l St ⋅=-⋅⎰⎰∂∂环路定理： d 0Sq E ε∑⋅=⎰内S 高斯定理：感生电场的计算：当磁场分布于圆柱形区域内且具有轴对称性时，可利用感生电场的环路定理计算出感生电场的空间分布。

d d LSBE l St ⋅=-⋅⎰⎰感生∂∂)(t B RLr d d 2r B E t=-感生当 r < R 时， d d 22R B E r t=-感生当 r > R 时，感生电场线为以对称轴为中心的同心圆环。

关于感生电场的方向和感生电场环路中负号的讨论。

d d LSBE l St ⋅=-⋅⎰⎰感生∂∂ 负号源自法拉第电磁感应定律，与感生电场的方向有关。

i d d d 感LE l tΦε=⋅=-⎰由楞次定律，负号可理解为感生电场及相应的感应电流的效果总是反抗或阻止引起它的原因。

由于电流激发磁场遵循右手螺旋定则，自然地，磁场变化的方向与其所激发感生电场的方向间就构成左手螺旋关系。

由于环路积分的方向与面积分中面元矢量的正法线方向满足右手螺旋定则，其中的负号当然就说明的方向与 的方向满足左手螺旋定则。

∂∂B t E 感生在感生电场中电磁感应定律可写成式中 为感应电场中的电场强度。

此式表明： (A) 闭合曲线 L 上处处相等。

(B) 感应电场是保守电场。

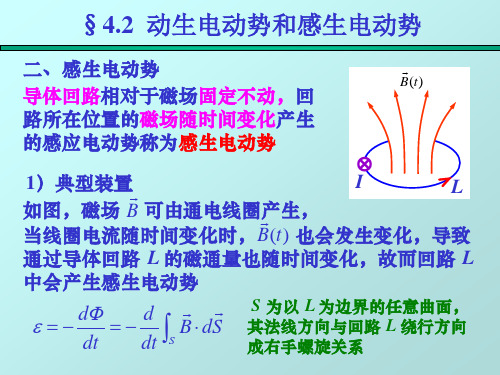
感生电动势一、感生电动势当一个相对静止的导体闭合回路处于随时间变化的磁场中时，穿过导体闭合回路的磁通量也会发生变化，导体中产生感应电动势，称为感生电动势。

二、感生电场1、麦克斯韦假设相对静止的导体闭合回路因磁场变化能产生感生电动势，这说明回路中的电荷由于磁场的变化受到了某种力的作用。

电荷受力的作用分为两种，一种是静电场所施的库仑力，另一种是施于运动电荷的洛仑兹力。

然而，在产生感生电动势的过程中，即没有静电场也没有电荷的运动。

因此，感应电动势的非静既不是静电场的静电力，也不是洛仑兹力，我们用以前学过的知识已无法解释感生电动势的微观机制。

为了解释感生电动势非静电力的起源，英国科学家麦克斯韦提出一个假设：变化磁场在其周围空间会激发一种电场，这种电场称为感生电场或涡旋电场。

这种电场不管空间有无导体或导体回路，不管是介质还是真空它都存在。

这种感生电场对导体中电荷的作用力就是构成感应电动势的非静电力。

麦克斯韦的这一假设已被许多实验所证实。

2、感生电场的性质电场从起源上分为两种：一种是由电荷激发的静电场（库仑电场），用表示；另一种是由变化磁场激发的感生电场，用表示。

这两种电场有一个共同的特点，即对处于电场中的电荷有作用力。

但感生电场的电场力不同于库仑电场的电场力，它是一种非静电力。

如果在感生电场中放入导体，则导体中的在感生电场力的作用下将发生定向运动，在导体中形成电动势；如果导体构成闭合回路，就产生感应电流。

因此，感生电动势的非静电力就是感生电场力，它是形成感生电动势的起因和本质。

根据定义，感生电动势等于感生电场沿某一闭合曲线的线积分，即根据法拉第电磁感应定律，有其中是穿过闭合曲线所包围曲面上的磁通量，即则由于和静止不动，故上式右边对曲面的积分和对时间的积分次序可以互换，因而有感生电场沿的积分方向就是感生电动势是正方向，它与回路法线矢量构成右手螺旋关系。

一般情况下，空间可能既存在电荷，又存在变化的磁场，因而它们激发的两种电场也就可能同时存在。

线圈感生电动势公式
线圈感生电动势（emf）是指当磁通量通过一个线圈发生变化时，在线圈内感应产生的电动势。

根据法拉第电磁感应定律，线圈感生电动势的大小与磁通量变化速率成正比。

线圈感生电动势的公式可以表示为：
emf = -N * dΦ/dt
其中：
•emf代表感生电动势，单位为伏特（V）
•N代表线圈的匝数
•dΦ/dt代表单位时间内磁通量的变化率，单位为韦伯/秒（Wb/s）
根据这个公式，当线圈内的磁通量变化快时，感生电动势就会变大；当线圈的匝数增加时，感生电动势也会增大。

需要注意的是，这个公式是一个理想情况下的近似表达式，实际情况可能会受到其他因素的影响，如电阻、自感等。

为了测量感生电动势，通常需要使用合适的电路和测量仪器。

同学们好！1.诱因：导体回路不动，由于磁场变化产生的感应电动势叫感生电动势。

S t B N S B N t t ss m i rrr r d d d d d d ⋅∂∂−=⋅−=−=∫∫ψε§13-3 感生电动势感生电场一、感生电动势2. 产生感生电动势的非静电力？(1) 是不是洛仑兹力？0 ,0=×==B v q F v rr v 不是洛仑兹力(2) 会是什么非静电力？不是洛仑兹力，不是化学力，不是扩散力只可能是一种新型的电场力假设假设：存在一种不同于静电场的新类型的电场（感生电场、涡旋电场)。

它来源于磁场的变化，并提供产生感生电动势的非静电力。

非静电力：涡旋电场力（感生电场力）非静电场强：iK E E rr =感感E q F F K rr r ==由电动势定义：∫∫=⋅=LLK l E d r r感εlE i r r d ⋅由电动势定义：∫∫=⋅=LLK l E d r r感εlE r rd ⋅感由法拉第定律：S tB N t m rrd d d ⋅∂∂−=−=∫ψε感感生电场是非保守场（无势场、涡旋场）。

=⋅∫l E Lr rd 感S tB N r rd ⋅∂∂−∫得：负号：楞次定律的内容3.感生电场的基本性质又：感生电场线闭合成环d =⋅∫S E sr r感感生电场是无源场。

0d d >tB感E r 感E r Br 感E r 感E r 0d d <tB××××××××××××××××××B r4 . 两种电场比较由静止电荷激发由变化的磁场激发电场线为闭合曲线0d d >tBr 感E r Br 电场线为非闭合曲线静电场感生电场起源电场线形状比较∑∫=⋅内静qS E s 01d εr rd =⋅∫sS E r r感有源：无源：保守：d =⋅∫Ll E r r静=⋅∫l E Lrr d 感S tB N Sr rd ⋅∂∂−∫非保守（涡旋）：不能脱离源电荷存在可以脱离“源”在空间传播静静Eq F rr =感感E q F r r =静电场感生电场性质特点对场中电荷的作用相互联系比较作为产生的非静电力，可以引起导体中电荷堆积，从而建立起静电场.感F r感ε0d d >tBABBr −+感E r×××××××××θ（1）场的存在并不取决于空间有无导体回路存在，变化的磁场总是在空间激发电场。