(完整版)推理公式法计算

省推理公式计算设计洪水手册一、基本公式：推理公式是无资料地区由暴雨推求洪水比较常用的方法，我省中小型水利工程设计洪水的计算也通常采用这种方法（一般在流域面积200km 2以下采用）。

它是假定汇流时间降雨强度是均匀，并将汇形面积曲线概化为矩形，导出如下计算公式：当τ≥c t 时，即全面汇流情况下，F R Q m ττ278.0= (1)当τ<c t 时，即部分汇流情况下，F R F tc R Q tctc tc m τ278.0278.0==……..(2) 式中：m Q 为地表净峰流量(m 3/s )，F 为流域面积（km 2），tc F 为成峰的产流面积（即与tc 相应的部份面积中最大的一块，km 2）；τ为流域汇流历时（小时）；tc 为地表产流历时（小时）；τR 为汇流历时的最表净雨量（毫米）；tc R 为产流历时的地表净雨量（毫米）；0.278为换算系数。

二、设计暴雨的计算 1、查图法计算设计暴雨（1）查算设计流域各种历时的暴雨参数：根据设计流域所在地点，应用年最大各种历时的降雨量均值等值线图和变差系数等值线图，按地理插法读取流域中心点的暴雨参数值，如果流域有两条以上等值线通过，可按面积加权法计算。

（2）计算设计频率的各种历时降雨量：根据上步查算的各种历时降雨量的变差系数Cv 值，从皮尔逊Ⅲ型曲线的模比系数K P 值表中（Cs/Cv=3.5）分别读取设计频率P 的K P 值，乘以相应的历时降雨量均值即得。

（3）计算各种历时的面雨量：根据设计流域的面积和降雨历时，查读暴雨点面关系表（附表1），得暴雨点面折算系数α，乘以相应的点雨量即得（流域面积在10km 2以下直接采用点雨量，不打折扣）。

（4）推求设计雨量的时程分配：把上面所求的设计降雨量代入24小时（或三天）的设计雨型表（附表3），即得设计雨量的时程分配。

（5）设计净雨的计算：24小时的设计雨量不扣损，直接用设计雨量过程作为设计净雨过程。

福建省推理公式计算设计洪水手册一、基本公式：推理公式是无资料地区由暴雨推求洪水比较常用的方法，我省中小型水利工程设计洪水的计算也通常采用这种方法（一般在流域面积200km 2以下采用）。

它是假定汇流时间内降雨强度是均匀，并将汇形面积曲线概化为矩形，导出如下计算公式：当τ≥c t 时，即全面汇流情况下，F R Q m ττ278.0= (1)当τ<c t 时，即部分汇流情况下，F R F tc R Q tctc tc m τ278.0278.0==……..(2) 式中：m Q 为地表净峰流量(m 3/s )，F 为流域面积（km 2），tc F 为成峰的产流面积（即与tc 相应的部份面积中最大的一块，km 2）；τ为流域汇流历时（小时）；tc 为地表产流历时（小时）；τR 为汇流历时内的最大地表净雨量（毫米）；tc R 为产流历时内的地表净雨量（毫米）；0.278为换算系数。

二、设计暴雨的计算 1、查图法计算设计暴雨（1）查算设计流域各种历时的暴雨参数：根据设计流域所在地点，应用年最大各种历时的降雨量均值等值线图和变差系数等值线图，按地理内插法读取流域中心点的暴雨参数值，如果流域内有两条以上等值线通过，可按面积加权法计算。

（2）计算设计频率的各种历时降雨量：根据上步查算的各种历时降雨量的变差系数Cv 值，从皮尔逊Ⅲ型曲线的模比系数K P 值表中（Cs/Cv=3.5）分别读取设计频率P 的K P 值，乘以相应的历时降雨量均值即得。

（3）计算各种历时的面雨量：根据设计流域的面积和降雨历时，查读暴雨点面关系表（附表1），得暴雨点面折算系数α，乘以相应的点雨量即得（流域面积在10km 2以下直接采用点雨量，不打折扣）。

（4）推求设计雨量的时程分配：把上面所求的设计降雨量代入24小时（或三天）的设计雨型表（附表3），即得设计雨量的时程分配。

（5）设计净雨的计算：24小时的设计雨量不扣损，直接用设计雨量过程作为设计净雨过程。

0.489 0.489
径流分配系
F（km2）
湖南省最大24小时降雨概化过程线（计算取值）
湖南省最大24小时降雨概化过程线（一区）
湖南省最大24小时降雨概化过程线（二区）
湖南省最大24小时降雨概化过程线（三区）
湖南省最大24小时降雨概化过程线（四区）
湖南省最大24小时降雨概化过程线（五区）
湖南省最大24小时降雨概化过程线（六区）
湖南省最大24小时降雨概化过程线（七区）
湖南省最大24小时降雨概化过程线（八区）
湖南省暴雨点面关系表：设计暴雨的点面关系系数α～流域面积F（km2）～降
t ～流域面积F（km 2）～降雨时间t关系
Q m/∑Q i。

广东省公务员考试科学推理解题技巧：1.掌握常考公式2.受力分析3.运用生活常识进行推理判断1.杠杆原理：杠杆保持平衡的条件：2211L F L F ∙=∙（L 是支点到力的作用线的距离）2.平抛运动的物体(1)水平速度：0v(2)竖直速度=0(3)水平距离t v s 0=(4)竖直距离221gt h = (5)在t 时刻的竖直速度：gt v t =3.匀变速运动的物体 (1)2021at t v s += (2)at v v t +=0(3)as v v t 2202=-(4)A.B 中间时刻即时速度ts v v v t t =+=202 (5)AB 位移中点的即时速度22202t s v v v += (6)匀速22s t v v =4.动能、重力势能mgh E mv E p K ==重力势能动能,212 机械守恒定律：机械能=动能+重力势能+弹性势能5.物体的浮沉条件 G 物 =ρ物gV 物 F 浮 =ρ液gV 排F 浮＝G 液排＝ρ液gV 排。

（V 排表示物体排开液体的体积）当物体漂浮时：F 浮＝G 物 且 ρ物<ρ液 当物体悬浮时：F 浮＝G 物 且 ρ物=ρ液 当物体上浮时：F 浮>G 物 且 ρ物<ρ液 当物体下沉时：F 浮<G 物 且 ρ物>ρ液 浮力F 浮规律一：物体漂浮在液体中，所受的浮力等于它受的重力；规律二：同一物体在不同液体里，所受浮力相同；规律三：同一物体在不同液体里漂浮，在密度大的液体里浸入的体积小；规律四：漂浮物体浸入液体的体积是它总体积的几分之几，物体密度就是液体密度的几分之几；规律五：将漂浮物体全部浸入液体里，需加的竖直向下的外力等于液体对物体增大的浮力。

当物体浸没在液体中时，V 物= V 排= Vρ物<ρ液 G 物< F 浮 上浮至漂浮ρ物=ρ液 G 物 = F 浮 悬浮ρ物>ρ液 G 物> F 浮 下沉至底6.合力在同一直线上：21F F F ±=不在同一直线上，成角度θ，合力θCOS F F F F F 21222122++=合力的大小随着角度的增加而减小，合力可以大于分力，可以等于分力，也可以小于分力。

2020年公务员行测考点:数学推理公式1、分数比例形式整除若a∶b=m∶n(m、n互质)，则a是m的倍数，b是n的倍数。

若a=m/n×b，则a=m/(m+n)×(a+b)，即a+b是m+n的倍数2、尾数法(1)选项尾数不同，且运算法则为加、减、乘、乘方运算，优先使用尾数进行判定;(2)所需计算数据多，计算复杂时考虑尾数判断快速得到答案。

常用在容斥原理中。

3、等差数列相关公式和=(首项+末项)×项数÷2=平均数×项数=中位数×项数;项数=(末项-首项)÷项数+1。

从1开始，连续的n个奇数相加，总和=n×n，如：1+3+5+7=4×4=16，……4、几何边端问题相关公式(1)单边线型植树公式(两头植树)：棵树=总长÷间隔+1，总长=(棵树-1)×间隔(2)植树不移动公式：在一条路的一侧等距离栽种m棵树，然后要调整为种n棵树，则不需要移动的树木棵树为：(m-1)与(n-1)的最大公约数+1棵;(3)单边环型植树公式(环型植树)：棵树=总长÷间隔，总长=棵树×间隔(4)单边楼间植树公式(两头不植)：棵树=总长÷间隔-1，总长=(棵树+1)×间隔(5)方阵问题：最外层总人数=4×(N-1)，相邻两层人数相差8人，n阶方阵的总人数为n?。

5、行程问题(1)火车过桥核心公式：路程=桥长+车长(火车过桥过的不是桥，而是桥长+车长)(2)相遇追及问题公式：相遇距离=(速度1+速度2)×相遇时间追及距离=(速度1-速度2)×追及时间(3)队伍行进问题公式：队首→队尾：队伍长度=(人速+队伍速度)×时间;队尾→队首：队伍长度=(人速-队伍速度)×时间(4)流水行船问题公式：顺速=船速+水速，逆速=船速-水速(5)往返相遇问题公式：两岸型两次相遇：S=3S1-S2，(第一次相遇距离A为S1，第二次相遇距离B为S2)单岸型两次相遇：S=(3S1+S2)/2，(第一次相遇距离A为S1，第二次相遇距离A为S2);左右点出发：第N次迎面相遇，路程和=(2N-1)×全程;第N次追上相遇，路程差=(2N-1)×全程。

不讲只看可能效果不明显，但还是希望对大家有帮助计算问题【例1】173×173×173－162×162×162＝（）A.926183B.936185C.926187D.926189尾数法，答案为D【例2++++ A. B. 2 C.D. 3平方差公式有理化，答案为B 【例3】9919+9919×2+9919×3…+9919×10＝（ ）。

A.991900 B.99190C. 11190D.995提取公因子后，等差数列求和，答案为D【例4】有一堆粗细均匀的圆木最上面一层有6根，每向下一层增长一根；共堆了25层。

这堆圆木共有多少根?A. 175B. 200C. 375D. 450等差数列通项公式和求和公式，答案为D【例5】某成衣厂对9名缝纫工进行技术评比，9名工人的得分恰好成等差数列，9人的平均得分是86分，前5名工人的得分之和是460分，那么前7名工人的得分之和是多少?（）A. 602B. 623C. 627D. 631利用中位数，答案B【例6】小赵，小钱，小孙，小李，小周五个人的收入依次成等比，已知小赵的收入是3000元，小孙的收入是3600元，那么小周比小孙的收入高：A．700元 B.720元C．760元 D.780元答案B【例7】有甲、乙、丙三辆公交车于上午8：00同时从公交总站出发，三辆车再次回到公交总站所用的时间分别为40分钟、25分钟和50分钟。

假设这三辆公交车中途不休息，请问它们下次同时到达公交总站将会是几点?( )A.11点20分B.11点整C.11点40分D.12点整最小公倍数，答案A容斥问题【例1】某单位对60名工作人员进行行政许可法测验，在第一次测验中有27人得满分，在第二次测验中有32人得满分。

如果两次测验中都没有得满分的有17人，那么两次测验中都获得满分的人数是（）A.12人B.13人C.16人D.20人两集合公式，答案为C【例2】运动会上100名运动员排成一列，从左向右依次编号为1-100，选出编号为3的倍数的运动员参加开幕式队列，而编号为5的倍数的运动员参加闭幕式队列。

备战公务员笔试判断推理必须记住的6组公式备战公务员笔试是一个相对复杂和综合的过程，需要广泛而深入的知识储备以及一定的逻辑推理能力。

其中，判断推理是考察候选人逻辑思维能力和分析问题的能力的重要部分。

下面是六组公式，希望对备战公务员笔试判断推理部分的候选人有所帮助。

一、充分必要条件公式在判断推理题中，很多题目都需要根据给出的条件进行判断或推理，而这些条件通常包含了充分条件和必要条件。

充分条件表示如果条件成立，则结论一定成立；必要条件表示如果结论成立，则条件一定成立。

在解答题目时必须准确理解条件之间的关系，才能正确完成判断或推理。

例题：条件：如果下雨了，那么路面湿滑。

结论：路面湿滑，则一定下雨了。

根据充分必要条件公式，如果路面湿滑，则一定下雨了。

但是，如果下雨了，路面是否湿滑不能确切得知。

因此，结论不能成立。

二、排列组合公式排列组合在判断推理题中常常涉及到，它是组合数学中的一个重要概念。

排列是从n个元素中取出m个元素按一定顺序排列，不重复；组合是从n个元素中取出m个元素，不考虑顺序排列，不重复。

熟练掌握排列组合的计算公式，能够在解答题目时节省时间并减少错误。

例题：条件：A、B、C、D、E这5个人排成一排。

结论：A排在B的前面，C排在D的前面。

根据排列组合公式，5个人排成一排总共有5!种可能性，而A排在B 前面、C排在D前面的情况只是其中一种。

因此，结论成立。

三、逻辑联结词公式逻辑联结词是判断推理题中常用的关键词，如“如果……，那么……”、“或者”、“并且”等。

逻辑联结词的正确理解和运用对于准确解答题目至关重要。

例题：条件：如果今天是星期天，那么明天是星期一结论：要么今天不是星期天，要么明天不是星期一根据逻辑联结词公式，如果今天是星期天，则明天必定是星期一、因此，结论不能成立。

四、逻辑关系公式在判断推理题中，常常需要分析或推测条件之间的逻辑关系。

逻辑关系包括充分条件、必要条件、充分必要条件、充分不必要条件等。

福建省推理公式计算设计洪水手册一、基本公式：推理公式是无资料地区由暴雨推求洪水比较常用的方法，我省中小型水利工程设计洪水的计算也通常采用这种方法（一般在流域面积200km 2以下采用）。

它是假定汇流时间内降雨强度是均匀，并将汇形面积曲线概化为矩形，导出如下计算公式：当τ≥c t 时，即全面汇流情况下，F R Q m ττ278.0= (1)当τ<c t 时，即部分汇流情况下，F R F tc R Q tctc tc m τ278.0278.0==……..(2) 式中：m Q 为地表净峰流量(m 3/s )，F 为流域面积（km 2），tc F 为成峰的产流面积（即与tc 相应的部份面积中最大的一块，km 2）；τ为流域汇流历时（小时）；tc 为地表产流历时（小时）；τR 为汇流历时内的最大地表净雨量（毫米）；tc R 为产流历时内的地表净雨量（毫米）；0.278为换算系数。

二、设计暴雨的计算 1、查图法计算设计暴雨（1）查算设计流域各种历时的暴雨参数：根据设计流域所在地点，应用年最大各种历时的降雨量均值等值线图和变差系数等值线图，按地理内插法读取流域中心点的暴雨参数值，如果流域内有两条以上等值线通过，可按面积加权法计算。

（2）计算设计频率的各种历时降雨量：根据上步查算的各种历时降雨量的变差系数Cv 值，从皮尔逊Ⅲ型曲线的模比系数K P 值表中（Cs/Cv=3.5）分别读取设计频率P 的K P 值，乘以相应的历时降雨量均值即得。

（3）计算各种历时的面雨量：根据设计流域的面积和降雨历时，查读暴雨点面关系表（附表1），得暴雨点面折算系数α，乘以相应的点雨量即得（流域面积在10km 2以下直接采用点雨量，不打折扣）。

（4）推求设计雨量的时程分配：把上面所求的设计降雨量代入24小时（或三天）的设计雨型表（附表3），即得设计雨量的时程分配。

（5）设计净雨的计算：24小时的设计雨量不扣损，直接用设计雨量过程作为设计净雨过程。

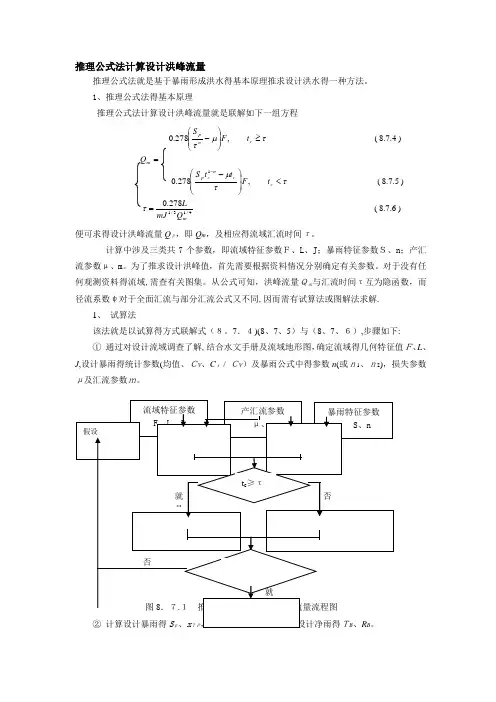
推理公式法计算设计洪峰流量推理公式法就是基于暴雨形成洪水得基本原理推求设计洪水得一种方法。

1、推理公式法得基本原理推理公式法计算设计洪峰流量就是联解如下一组方程)6.7.8(278.0)5.7.8(,278.0)4.7.8(,278.04/13/11mc cn cp m c n p Q mJ L t F t t SQ t F S =<⎪⎪⎭⎫⎝⎛-=≥⎪⎪⎭⎫⎝⎛--τττμτμτ便可求得设计洪峰流量Q ｐ，即Q m ，及相应得流域汇流时间τ。

计算中涉及三类共7个参数，即流域特征参数Ｆ、L 、J ；暴雨特征参数Ｓ、n ；产汇流参数μ、m 。

为了推求设计洪峰值，首先需要根据资料情况分别确定有关参数。

对于没有任何观测资料得流域,需查有关图集。

从公式可知，洪峰流量Ｑｍ与汇流时间τ互为隐函数，而径流系数ψ对于全面汇流与部分汇流公式又不同,因而需有试算法或图解法求解.1、 试算法该法就是以试算得方式联解式（８。

7．４)(8、7、5）与（8、7、６）,步骤如下: ① 通过对设计流域调查了解,结合水文手册及流域地形图，确定流域得几何特征值Ｆ、L 、J ,设计暴雨得统计参数(均值、ＣV 、C ｓ / ＣV ）及暴雨公式中得参数n (或ｎ1、ｎ2)，损失参数μ及汇流参数ｍ。

③ 将F 、Ｌ、J 、R B 、T B 、m 代入式（８。

7．4）(8、7、5）与（8、7、6)，其中仅剩下Q m 、τ、R s,τ未知,但R s ，τ与τ有关，故可求解.④ 用试算法求解。

先设一个Ｑm ,代入式（８.７.6）得到一个相应得τ，将它与t c 比较,判断属于何种汇流情况，再将该τ值代入式(8、7、4)或式（8、7、5)，又求得一个Q m ,若与假设得一致（误差不超过1％）,则该Q m 及τ即为所求;否则,另设Q m 仿以上步骤试算，直到两式都能共同满足为止。

试算法计算框图如图８．７。

1。

２、 图解交点法该法就是对（8。

7。