水文计算(推理公式法)
- 格式:xls
- 大小:30.50 KB
- 文档页数:4

水文计算步骤推理公式法计算设计洪峰流量推理公式法是基于暴雨形成洪水的基本原理推求设计洪水的一种方法。
1.推理公式法的基本原理推理公式法计算设计洪峰流量是联解如下一组方程)6.7.8(278.0)5.7.8(,278.0)4.7.8(,278.04/13/11mc cn cp m c n p Q mJ L t F t t S Q t F S =<⎪⎪⎭⎫⎝⎛-=≥⎪⎪⎭⎫⎝⎛--τττμτμτ便可求得设计洪峰流量Q p ,即Q m ,及相应的流域汇流时间τ。
计算中涉及三类共7个参数,即流域特征参数F 、L 、J ;暴雨特征参数S 、n ;产汇流参数μ、m 。
为了推求设计洪峰值,首先需要根据资料情况分别确定有关参数。
对于没有任何观测资料的流域,需查有关图集。
从公式可知,洪峰流量Q m 和汇流时间τ互为隐函数,而径流系数ψ对于全面汇流和部分汇流公式又不同,因而需有试算法或图解法求解。
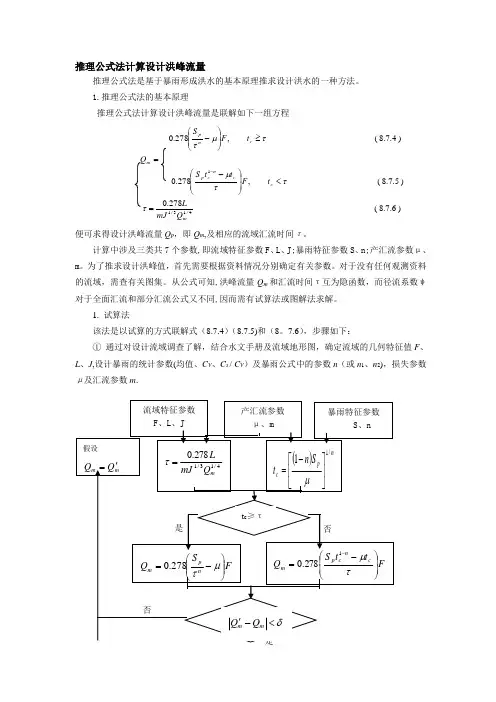
1. 试算法该法是以试算的方式联解式(8.7.4)(8.7.5)和(8.7.6),步骤如下:① 通过对设计流域调查了解,结合水文手册及流域地形图,确定流域的几何特征值F 、L 、J ,设计暴雨的统计参数(均值、C V 、C s / C V )及暴雨公式中的参数n (或n 1、n 2),损失参数μ及汇流参数m 。
图8.7.1 推理公式法计算设计洪峰流量流程图② 计算设计暴雨的S p 、x TP ,进而由损失参数μ计算设计净雨的T B 、R B 。
③ 将F 、L 、J 、R B 、T B 、m 代入式(8.7.4)(8.7.5)和(8.7.6),其中仅剩下Q m 、τ、R s,τ未知,但R s,τ与τ有关,故可求解。
④ 用试算法求解。
先设一个Q m ,代入式(8.7.6)得到一个相应的τ,将它与t c 比较,判断属于何种汇流情况,再将该τ值代入式(8.7.4)或式(8.7.5),又求得一个Q m ,若与假设的一致(误差不超过1%),则该Q m 及τ即为所求;否则,另设Q m 仿以上步骤试算,直到两式都能共同满足为止。
推理公式法计算设计洪峰流量推理公式法是基于暴雨形成洪水的基本原理推求设计洪水的一种方法。
1.推理公式法的基本原理推理公式法计算设计洪峰流量是联解如下一组方程)6.7.8(278.0)5.7.8(,278.0)4.7.8(,278.04/13/11mc cn cp m c n p Q mJ L t F t t SQ t F S =<⎪⎪⎭⎫⎝⎛-=≥⎪⎪⎭⎫⎝⎛--τττμτμτ便可求得设计洪峰流量Q p ,即Q m ,及相应的流域汇流时间τ。
计算中涉及三类共7个参数,即流域特征参数F 、L 、J;暴雨特征参数S 、n;产汇流参数μ、m 。
为了推求设计洪峰值,首先需要根据资料情况分别确定有关参数。
对于没有任何观测资料的流域,需查有关图集。
从公式可知,洪峰流量Q m 和汇流时间τ互为隐函数,而径流系数ψ对于全面汇流和部分汇流公式又不同,因而需有试算法或图解法求解。
1. 试算法该法是以试算的方式联解式(8.7.4)(8.7.5)和(8。
7.6),步骤如下:① 通过对设计流域调查了解,结合水文手册及流域地形图,确定流域的几何特征值F 、L 、J ,设计暴雨的统计参数(均值、C V 、C s / C V )及暴雨公式中的参数n (或n 1、n 2),损失参数μ及汇流参数m .图8.7。
1 推理公式法计算设计洪峰流量流程图② 计算设计暴雨的S p 、x TP ,进而由损失参数μ计算设计净雨的T B 、R B 。
③ 将F 、L 、J 、R B 、T B 、m 代入式(8.7。
4)(8.7.5)和(8.7。
6),其中仅剩下Q m 、τ、R s ,τ未知,但R s,τ与τ有关,故可求解。
④ 用试算法求解。
先设一个Q m ,代入式(8.7.6)得到一个相应的τ,将它与t c 比较,判断属于何种汇流情况,再将该τ值代入式(8。
7。
4)或式(8.7。
5),又求得一个Q m ,若与假设的一致(误差不超过1%),则该Q m 及τ即为所求;否则,另设Q m 仿以上步骤试算,直到两式都能共同满足为止.试算法计算框图如图8.7。

桥涵水文分析与计算一、概述桥涵水文分析与计算,包括河流水文资料的调查搜集整理与计算,推求出我们桥涵所需要的设计水位和流量,拟定出桥长孔径、桥高和基础埋设深度。
由于桥位所处的地理位置不同以及其它复杂因素,包括天然的和人为因素如潮汐、泥石流、修水库、开挖渠道等。
我们调查搜集洪水流量的计算方法各有不同。
水文计算从大的方面来分:有水文(雨量)观测资料和无水文观测资料的水文计算。
从各河段特殊情况的不同又可分为,有水库的水文计算,倒灌河流的水文计算,平原或者山丘区的水文计算,还有潮汐河段、岩溶河段、泥石流河段等。
不同情况的河流我们要有针对性的调查,搜集有关资料调查搜集资料很辛苦,跑路多收效有时还很小,但工作必需要做,要有耐心。
需要调查搜集的资料综合起来有:水系图,县志和水利志、地形图、形态断面、水文站(气象站)资料水库资料,倒灌资料、河道演度、河床淤积、雨力资料、洪水调查及比降的测量,原有桥涵的调查等,通过调查为下步洪水设计流量提供有关参数。
另外还要进行地质地貌调查,有些设计流量的计算参数也和土的颗粒组成、土壤的分类、密实度吸水率熔洞泥石流等有关,有的与设计流量无关,但与桥的安全性有关如土体稳定性、山体滑坡、湿陷性黄土软土地基等,一般野外采用看挖钻的方法,下面介绍一下土壤分类的一般常识,分为三类:1.粘性土:塑性指数p I >1 亚砂土或轻亚粘土1<p I ≤7; 亚粘土 7<I ≤17; 粘土 p I ≥17;塑性指数p I =l W (液限)-p W (塑限);而粘性土壤的状态用液性指数(即稠度系数)l I 分为四级,l I =pl p o w w w w --;o W —天然含水量;l I <0为坚硬半坚硬 标贯>3.5; 0≤l I <0.5为硬塑 标贯>-3.5; 0.5≤l I <1为软塑 标贯<-7;l I ≥1 为极软 标贯<2;淤泥是极软状态的粘性土,其含水量接近或大于液限,对于孔隙比大于1的轻亚粘土或亚粘土和孔隙比大于1.5的粘土均称淤泥。

0.489 0.489
径流分配系
F(km2)
湖南省最大24小时降雨概化过程线(计算取值)
湖南省最大24小时降雨概化过程线(一区)
湖南省最大24小时降雨概化过程线(二区)
湖南省最大24小时降雨概化过程线(三区)
湖南省最大24小时降雨概化过程线(四区)
湖南省最大24小时降雨概化过程线(五区)
湖南省最大24小时降雨概化过程线(六区)
湖南省最大24小时降雨概化过程线(七区)
湖南省最大24小时降雨概化过程线(八区)
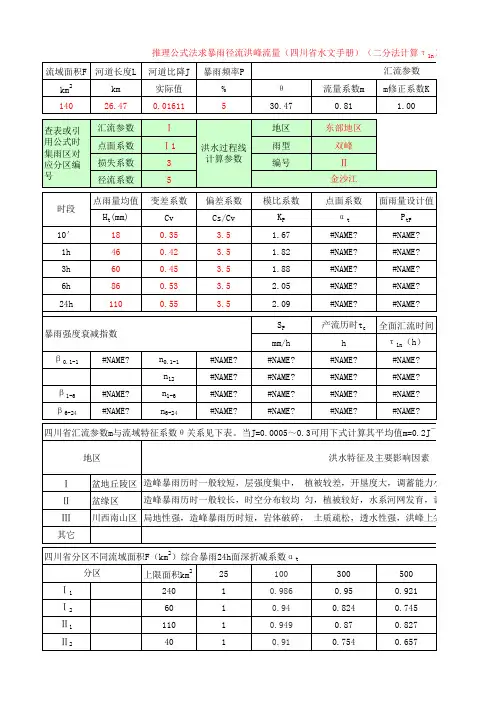
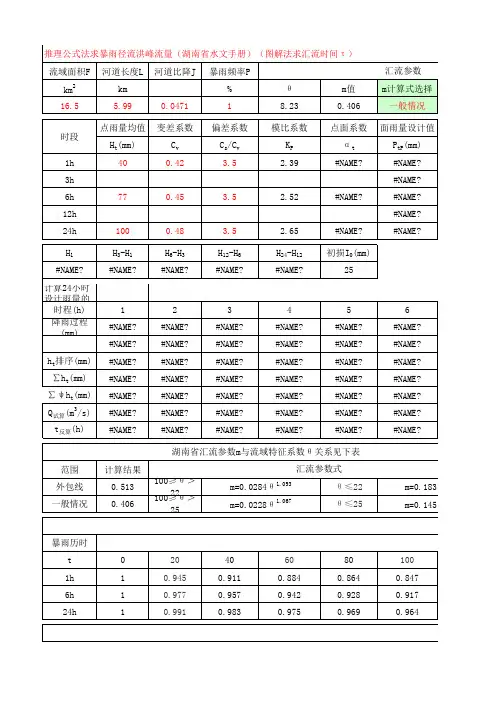
湖南省暴雨点面关系表:设计暴雨的点面关系系数α~流域面积F(km2)~降
t ~流域面积F(km 2)~降雨时间t关系
Q m/∑Q i。

一、重现期重现期是指平均多少年重复出现一次,或多少年一遇。
频率P 与重现期T 的关系,对下列两种不同情况有不同的表示方法。
研究暴雨洪水问题时,一般设计频率小于50%,则T=1/PT 表示大于某值降雨量的重现期例如:当设计洪水的频率为P=1%时,代入上式得T=100a ,称为百年一遇。
研究枯水问题时,为了保证灌溉、发电及给水等用水需要,设计频率P 常采用大于50%,则T=1/(1-P)T 表示小于某值降雨量的重现期例如:当灌溉设计保证率P=90%,代入式中得T=10a ,称为10年一遇的枯水年。
若以此作为设计来水的标准,则说明平均10年中有一年来水小于此枯水年的水量,而其余几年的来水等于或大于此数值,也就是说平均具有90%的可靠程度。
均方差σ:又称标准差,说明系列离散程度。
变差系数Cv :又称离势系数、离差系数表示标准差相对于平均数大小的相对量,反映频率密度分配曲线的平均情况和离散程度。
偏态系数Cs :又称偏差系数,说明随机系列分配不对称程度的统计参数。
当随机变量大于均值与小于均值的出现机会相等时,即当系列取值对称与x 时,Cs=0,此时均值所对应的频率为50%。
当小于均值的出现机会多时,均值所对应的频率大于50%,Cs>0,为正偏(或右偏);当大于均值的出现机会多时,均值所对应的频率小于50%, Cs<0。
()nxXni i∑=-=12σ ()nKxC ni i∑=-==12v 1σ()()313331s 1vni ini inCKnx x C ∑∑==-=-=σ离均系数Φp :是对随机变量进行标准化处理后得到的随机变量,是标准化变量,Φ的均值为0,标准差为1。
(皮尔逊Ⅲ型频率曲线的离均系数Φp 值表) 模比系数Kp :某一时段内的径流模数与较长时段内的平均径流模数的比值。
v C x x x -=Φ ()Φ+=v C x x 1 xx K p P =二、洪峰流量1、推理公式法:①洪峰流量(集雨面积小于2km 2) 洪峰流量按下式计算: Q s =0.278KIF式中:Q s —洪峰流量; K —径流系数,取0.9;I —最大1h 降雨强度(mm/h ),查《四川省中小流域暴雨洪水计算手册》计算得5年一遇最大1h 降雨强度56.7mm ;11H K I P •= F —集水面积(km 2),根据地形图及项目区实际情况确定。

水文计算步骤推理公式法计算设计洪峰流量推理公式法是基于暴雨形成洪水的基本原理推求设计洪水的一种方法。
1.推理公式法的基本原理推理公式法计算设计洪峰流量是联解如下一组方程)6.7.8(278.0)5.7.8(,278.0)4.7.8(,278.04/13/11mc cn cp m c n p Q mJ L t F t t S Q t F S =<⎪⎪⎭⎫⎝⎛-=≥⎪⎪⎭⎫⎝⎛--τττμτμτ便可求得设计洪峰流量Q p ,即Q m ,及相应的流域汇流时间τ。
计算中涉及三类共7个参数,即流域特征参数F 、L 、J ;暴雨特征参数S 、n ;产汇流参数μ、m 。
为了推求设计洪峰值,首先需要根据资料情况分别确定有关参数。
对于没有任何观测资料的流域,需查有关图集。
从公式可知,洪峰流量Q m 和汇流时间τ互为隐函数,而径流系数ψ对于全面汇流和部分汇流公式又不同,因而需有试算法或图解法求解。
1. 试算法该法是以试算的方式联解式(8.7.4)(8.7.5)和(8.7.6),步骤如下:① 通过对设计流域调查了解,结合水文手册及流域地形图,确定流域的几何特征值F 、L 、J ,设计暴雨的统计参数(均值、C V 、C s / C V )及暴雨公式中的参数n (或n 1、n 2),损失参数μ及汇流参数m 。
图8.7.1 推理公式法计算设计洪峰流量流程图② 计算设计暴雨的S p 、x TP ,进而由损失参数μ计算设计净雨的T B 、R B 。
③ 将F 、L 、J 、R B 、T B 、m 代入式(8.7.4)(8.7.5)和(8.7.6),其中仅剩下Q m 、τ、R s,τ未知,但R s,τ与τ有关,故可求解。
④ 用试算法求解。
先设一个Q m ,代入式(8.7.6)得到一个相应的τ,将它与t c 比较,判断属于何种汇流情况,再将该τ值代入式(8.7.4)或式(8.7.5),又求得一个Q m ,若与假设的一致(误差不超过1%),则该Q m 及τ即为所求;否则,另设Q m 仿以上步骤试算,直到两式都能共同满足为止。

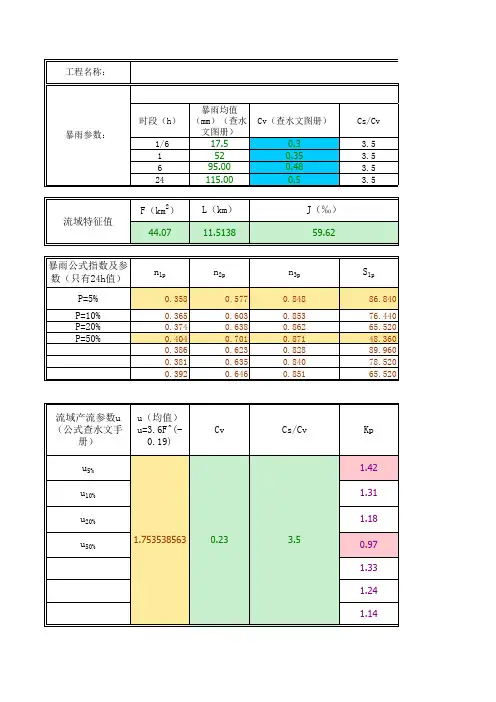

推理公式法计算设计洪峰流量推理公式法就是基于暴雨形成洪水得基本原理推求设计洪水得一种方法。
1、推理公式法得基本原理推理公式法计算设计洪峰流量就是联解如下一组方程)6.7.8(278.0)5.7.8(,278.0)4.7.8(,278.04/13/11mc cn cp m c n p Q mJ L t F t t SQ t F S =<⎪⎪⎭⎫⎝⎛-=≥⎪⎪⎭⎫⎝⎛--τττμτμτ便可求得设计洪峰流量Q p,即Q m ,及相应得流域汇流时间τ。
计算中涉及三类共7个参数,即流域特征参数F、L 、J ;暴雨特征参数S、n ;产汇流参数μ、m 。
为了推求设计洪峰值,首先需要根据资料情况分别确定有关参数。
对于没有任何观测资料得流域,需查有关图集。
从公式可知,洪峰流量Qm与汇流时间τ互为隐函数,而径流系数ψ对于全面汇流与部分汇流公式又不同,因而需有试算法或图解法求解.1、 试算法该法就是以试算得方式联解式(8。
7.4)(8、7、5)与(8、7、6),步骤如下: ① 通过对设计流域调查了解,结合水文手册及流域地形图,确定流域得几何特征值F、L 、J ,设计暴雨得统计参数(均值、CV 、C s / CV )及暴雨公式中得参数n (或n1、n2),损失参数μ及汇流参数m。
③ 将F 、L、J 、R B 、T B 、m 代入式(8。
7.4)(8、7、5)与(8、7、6),其中仅剩下Q m 、τ、R s,τ未知,但R s ,τ与τ有关,故可求解.④ 用试算法求解。
先设一个Qm ,代入式(8.7.6)得到一个相应得τ,将它与t c 比较,判断属于何种汇流情况,再将该τ值代入式(8、7、4)或式(8、7、5),又求得一个Q m ,若与假设得一致(误差不超过1%),则该Q m 及τ即为所求;否则,另设Q m 仿以上步骤试算,直到两式都能共同满足为止。
试算法计算框图如图8.7。
1。
2、 图解交点法该法就是对(8。
7。
涵洞水文计算书根据《公路涵洞设计细则》(JTG/T D65-04—2007),四级公路涵洞设计洪水频率二十五年一遇(1/25),新建涵洞应采用无压力式涵洞,根据暴雨推理法相关公式,并结合现场实际情况,计算求得相应洪峰流量,从而选择合适的盖板涵尺寸以满足过洪要求。
1、暴雨推理公式F S Q npP μ)-=τ(278.0 (1-1)式中:Q P ——规定频率为P%的洪峰流量(m ³/s );S p ——频率为P%的雨力(rnm/h),查附录B 各省(区)雨力等值线图(图B-1~图B-3);τ——汇流时间(h);汇流时间二按下式计算:北方可采用13(ατ)ZI L K = (1-2) 南方可采用324(βατ-=P ZS I L K ) (1-3) 43K K 、——系数,查附录B 表B-1;L ——主河沟长度(km ); I Z ——主河沟平均坡度(0.001);321βαα、、——系数,查附录B 表B-1;n ——暴雨递减指数;查附录B 各省(区)暴雨递减指数n 值分区图(图B-4)和表B-2,表中n 1、n 2、n 3由τ值分查;μ——损失参数(mm/h);损失参数μ按下式计算:北方可采用11βμP S K = (1-4)南方可采用122λβμ-=F S K P(1-5) 21K K 、——系数,查附录B 表B-3,表中土壤植被分类,查附录B 表B-4;121λββ、、——指数,查附录B 表B-3; F ——汇水面积(km 2)。
2、推理公式中各参数的取值计算(1)流域特征值F ,L ,I ZF 、L 为计算流域的汇水面积及主沟长度,在Google Earth 地形图上勾画出流域范围后,直接量算得出;I Z 为主沟道纵坡,采用加权平均法计算得出。
有关流域特征参数计算结果见表2-1。
表2-1 流域特征值F 、J 、I Z(2)暴雨雨力S P根据设计洪水频率1/25,查《公路涵洞设计细则》JTG/T D65-04—2007附录B (图B-3)得暴雨雨力Sp 见表2-2。
⽔⽂分析计算1⽔⽂分析计算⽔⽂分析计算是规划的重要环节,是确定临⽔控制线、外缘控制线、划定河道管理范围的主要技术依据。
⽔⽂分析计算,包括准备⼯作、设计洪⽔计算、⽔⾯线计算等步骤。
应逐条河流、分段计算。
1.1准备⼯作准备⼯作包括选择控制断⾯,计算流域⾯积和控制集⽔⾯积,收集暴⾬洪⽔资料等。
1.选择控制断⾯。
控制断⾯应选择⼲流河⼝、拦河建筑物坝轴线、主要⽀流汇合⼝下游的顺直河段。
控制断⾯具体位置,根据规划河段的具体情况确定。
2.计算流域⾯积和控制集⽔⾯积。
流域⾯积为河⼝断⾯或控制断⾯以上,沿着分⽔岭勾绘的流域总⾯积;控制集⽔⾯积为规划河段典型控制断⾯以上,按照城市(城镇)规划,实际汇⼊规划河段的集⽔⾯积。
流域⾯积100km2及以上河流的流域⾯积,可直接采⽤《重庆市主要河流和城镇河道岸线保护与利⽤管理规划汇编》(2013年版)和区县政府已批准的集⽔⾯积1000-100km2以上河流的《河道岸线利⽤管理规划》(2008-2020)中的数据。
流域⾯积100km2以下河流的流域⾯积和控制集⽔⾯积,可在1:10000地形图上⽤求积仪计算。
流域地形图,以能画出分⽔岭和便于⾯积计算为准,要求图纸清晰。
3.收集暴⾬洪⽔资料。
通过实测、调查、分析等⽅式收集暴⾬洪⽔资料。
暴⾬洪⽔资料最好是本流域的实测洪⽔资料,或历史洪⽔调查资料。
1.2设计洪⽔计算设计洪⽔计算主要包括以下⼯作:⼀是选择暴⾬洪⽔计算依据或参证站,再根据代表站的数据资料情况;⼆是根据河道流域情况和设计洪⽔计算⽅法的适⽤条件选择与之符合的计算或推算⽅法;三是对设计洪⽔计算成果进⾏合理性分析,对设计洪⽔计算成果进⾏修订。
1.2.1依据站和参证站的选择依据站,应该为本河道的暴⾬洪⽔实测站点。
参证站,为与⽔⽂计算流域相关的站点。
应是邻近河流或邻近区域的站点,或与⽔⽂计算流域同属⼀个⾬区或产汇流关系相近的站点。
1.2.2计算⽅法1.2.2.1⽅法选择根据河段的具体情况,按《⽔利⽔电⼯程设计洪⽔计算规范》(SL44-2006)要求选⽤洪⽔计算⽅法。