三次Bezier曲线原理及实现代码

lv_bezier3 的用法lv_bezier3是一个用于贝塞尔曲线绘制的函数。

在这篇文章中，我们将逐步回答关于lv_bezier3的用法的问题，帮助读者了解如何使用这个函数绘制优雅的曲线。

第一步：了解贝塞尔曲线的基本概念贝塞尔曲线是一种数学曲线，它通过控制点来定义。

贝塞尔曲线可以用于绘制平滑的曲线，其形状由曲线上的控制点决定。

一般情况下，贝塞尔曲线由三个或四个控制点组成。

- 三次贝塞尔曲线（Cubic Bezier Curve）由两个端点和两个控制点定义。

- 二次贝塞尔曲线（Quadratic Bezier Curve）由一个起始点、一个结束点和一个控制点定义。

在绘制曲线之前，我们首先需要了解这些基本概念。

第二步：引入lvgl库lvgl是一个开源的图形库，可以用于嵌入式系统中的图形界面设计。

lvgl 库提供了各种绘图函数，包括贝塞尔曲线绘制函数lv_bezier3。

在使用lv_bezier3之前，我们需要引入lvgl库。

可以通过在代码中添加以下语句来实现：#include "lvgl/lvgl.h"这将导入lvgl库，我们就可以开始使用lv_bezier3函数。

第三步：使用lv_bezier3绘制曲线lv_bezier3函数的原型如下：void lv_bezier3(const point_t *points, point_t *out_p, uint16_t t);该函数接受一个包含四个点的数组point_t *points，以及一个指向point_t类型的输出数组out_p和一个0-1000之间的整数t。

out_p数组将包含曲线上的一系列点的坐标，用于绘制曲线。

参数t用于确定曲线上的点的数量，其中t=1000对应于曲线上的1000个点。

以下是一个使用lv_bezier3绘制三次贝塞尔曲线的示例代码：void draw_cubic_bezier(const point_t *points){point_t curve_points[1001]; 1000个点用于绘制曲线lv_bezier3(points, curve_points, 1000);绘制曲线代码}在这个示例中，我们首先创建一个数组curve_points，用于存储曲线上的点的坐标。

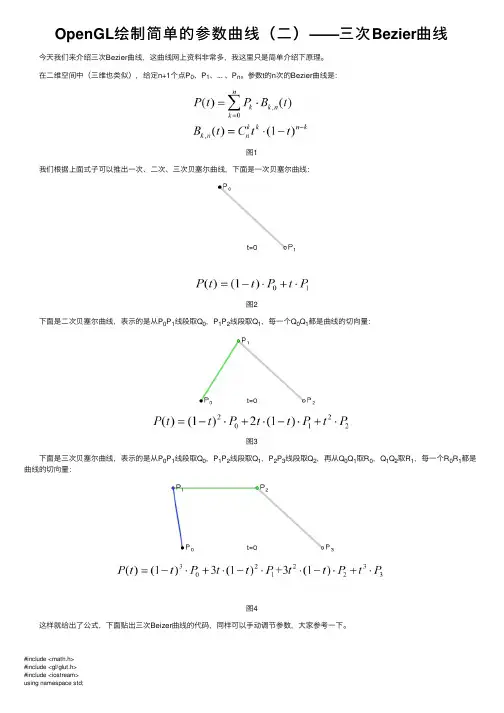
OpenGL绘制简单的参数曲线（⼆）——三次Bezier曲线 今天我们来介绍三次Bezier曲线，这曲线⽹上资料⾮常多，我这⾥只是简单介绍下原理。

在⼆维空间中（三维也类似），给定n+1个点P0、P1、... 、P n。

参数t的n次的Bezier曲线是：图1 我们根据上⾯式⼦可以推出⼀次、⼆次、三次贝塞尔曲线，下⾯是⼀次贝塞尔曲线：图2 下⾯是⼆次贝塞尔曲线，表⽰的是从P0P1线段取Q0，P1P2线段取Q1，每⼀个Q0Q1都是曲线的切向量：图3 下⾯是三次贝塞尔曲线，表⽰的是从P0P1线段取Q0，P1P2线段取Q1，P2P3线段取Q2，再从Q0Q1取R0，Q1Q2取R1，每⼀个R0R1都是曲线的切向量：图4 这样就给出了公式，下⾯贴出三次Beizer曲线的代码，同样可以⼿动调节参数，⼤家参考⼀下。

#include <math.h>#include <gl/glut.h>#include <iostream>using namespace std;int xCoord[4], yCoord[4];int num = 0;bool finishBeizer = false;bool mouseLeftDown = false;bool mouseRightDown = false;/*计算Bezier曲线*/void Bezier(int n){float f1, f2, f3, f4;float deltaT = 1.0 / n;float T;glBegin(GL_LINE_STRIP);for (int i = 0; i <= n; i++) {T = i * deltaT;f1 = (1-T) *(1- T) * (1-T);f2 = 3 * T * (1-T) * (1- T);f3 = 3 * T * T * (1-T);f4 = T * T * T;glVertex2f( f1*xCoord[0] + f2*xCoord[1] + f3*xCoord[2] + f4*xCoord[3], f1*yCoord[0] + f2*yCoord[1] + f3*yCoord[2] + f4*yCoord[3]);}glEnd();}/*⽤⿏标进⾏绘制，完成后可改变控制点，拖动即可*/void display(){glClear(GL_COLOR_BUFFER_BIT);glLineWidth(1.5);glColor3f (1.0, 0.0, 0.0);glBegin(GL_LINE_STRIP);for (int i = 0; i < num; i++)glVertex3f (xCoord[i], yCoord[i], 0.0);glEnd();glColor3f (0.0, 0.0, 1.0);if (num == 4)Bezier(20);glPointSize(10.0f);glBegin(GL_POINTS);glVertex2f(xCoord[0], yCoord[0]);glVertex2f(xCoord[1], yCoord[1]);glVertex2f(xCoord[2], yCoord[2]);glVertex2f(xCoord[3], yCoord[3]);glEnd();glFlush();glutSwapBuffers();}void init(){glClearColor(1.0, 1.0, 1.0, 0.0);glShadeModel(GL_FLAT);}void myReshape(int w, int h){glViewport(0, 0, (GLsizei)w, (GLsizei)h);glMatrixMode(GL_PROJECTION);glLoadIdentity();gluOrtho2D(0.0, (GLsizei)w, (GLsizei)h, 0.0);glMatrixMode(GL_MODELVIEW);glLoadIdentity();}void mouse(int button, int state, int x, int y){if (!finishBeizer){if (button == GLUT_LEFT_BUTTON && state == GLUT_DOWN){xCoord[num] = x;yCoord[num] = y;num++;if (num == 4)finishBeizer = true;glutPostRedisplay();}}else{if (button == GLUT_LEFT_BUTTON && state == GLUT_DOWN) {mouseLeftDown = true;}if (button == GLUT_LEFT_BUTTON && state == GLUT_UP){mouseLeftDown = false;}if (button == GLUT_RIGHT_BUTTON && state == GLUT_DOWN) {mouseRightDown = true;}if (button == GLUT_RIGHT_BUTTON && state == GLUT_UP){mouseRightDown = false;}}}double distance(int x1, int y1, int x2, int y2){return sqrt((x1-x2) * (x1 -x2) + (y1-y2) * (y1-y2));}void motion(int x, int y){if (mouseLeftDown){if (distance(xCoord[1], yCoord[1], x, y) < 20){xCoord[1] = x;yCoord[1] = y;}if (distance(xCoord[2], yCoord[2], x, y) < 20){xCoord[2] = x;yCoord[2] = y;}}glutPostRedisplay();}int main(int argc, char** argv){glutInit(&argc, argv);glutInitDisplayMode (GLUT_DOUBLE | GLUT_RGB );glutInitWindowSize (450, 450);glutInitWindowPosition (200, 200);glutCreateWindow ("hello");init ();glutDisplayFunc(display);glutReshapeFunc(myReshape);glutMouseFunc(mouse);glutMotionFunc(motion);glutMainLoop();return 0;}。

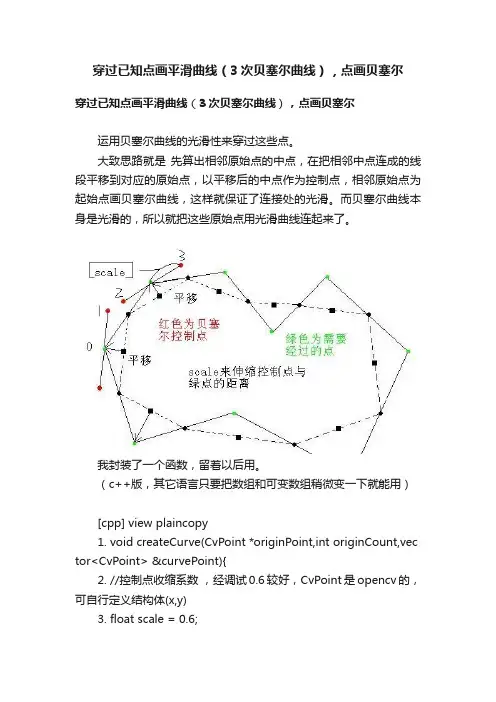
穿过已知点画平滑曲线（3次贝塞尔曲线），点画贝塞尔穿过已知点画平滑曲线（3次贝塞尔曲线），点画贝塞尔运用贝塞尔曲线的光滑性来穿过这些点。

大致思路就是先算出相邻原始点的中点，在把相邻中点连成的线段平移到对应的原始点，以平移后的中点作为控制点，相邻原始点为起始点画贝塞尔曲线，这样就保证了连接处的光滑。

而贝塞尔曲线本身是光滑的，所以就把这些原始点用光滑曲线连起来了。

我封装了一个函数，留着以后用。

（c++版，其它语言只要把数组和可变数组稍微变一下就能用）[cpp] view plaincopy1.void createCurve(CvPoint *originPoint,int originCount,vec tor<CvPoint> &curvePoint){2.//控制点收缩系数，经调试0.6较好，CvPoint是opencv的，可自行定义结构体(x,y)3.float scale = 0.6;4.CvPoint midpoints[originCount];5.//生成中点6.for(int i = 0 ;i < originCount ; i++){7.int nexti = (i + 1) % originCount;8.midpoints[i].x = (originPoint[i].x + originPoint[nexti].x)/2. 0;9.midpoints[i].y = (originPoint[i].y + originPoint[nexti].y)/2. 0;10.}11.12.//平移中点13.CvPoint extrapoints[2 * originCount];14.for(int i = 0 ;i < originCount ; i++){15.int nexti = (i + 1) % originCount;16.int backi = (i + originCount - 1) % originCount;17.CvPoint midinmid;18.midinmid.x = (midpoints[i].x + midpoints[backi].x)/2.0;19.midinmid.y = (midpoints[i].y + midpoints[backi].y)/2.0;20.int offsetx = originPoint[i].x - midinmid.x;21.int offsety = originPoint[i].y - midinmid.y;22.int extraindex = 2 * i;23.extrapoints[extraindex].x = midpoints[backi].x + offset x;24.extrapoints[extraindex].y = midpoints[backi].y + offset y;25.//朝 originPoint[i]方向收缩26.int addx = (extrapoints[extraindex].x - originPoint[i].x) * scale;27.int addy = (extrapoints[extraindex].y - originPoint[i].y) * scale;28.extrapoints[extraindex].x = originPoint[i].x + addx;29.extrapoints[extraindex].y = originPoint[i].y + addy;30.31.int extranexti = (extraindex + 1)%(2 * originCount);32.extrapoints[extranexti].x = midpoints[i].x + offsetx;33.extrapoints[extranexti].y = midpoints[i].y + offsety;34.//朝 originPoint[i]方向收缩35.addx = (extrapoints[extranexti].x - originPoint[i].x) * sc ale;36.addy = (extrapoints[extranexti].y - originPoint[i].y) * sc ale;37.extrapoints[extranexti].x = originPoint[i].x + addx;38.extrapoints[extranexti].y = originPoint[i].y + addy;39.40.}41.42.CvPoint controlPoint[4];43.//生成4控制点，产生贝塞尔曲线44.for(int i = 0 ;i < originCount ; i++){45.controlPoint[0] = originPoint[i];46.int extraindex = 2 * i;47.controlPoint[1] = extrapoints[extraindex + 1];48.int extranexti = (extraindex + 2) % (2 * originCount);49.controlPoint[2] = extrapoints[extranexti];50.int nexti = (i + 1) % originCount;51.controlPoint[3] = originPoint[nexti];52.float u = 1;53.while(u >= 0){54.int px = bezier3funcX(u,controlPoint);55.int py = bezier3funcY(u,controlPoint);56.//u的步长决定曲线的疏密57.u -= 0.005;58.CvPoint tempP = cvPoint(px,py);59.//存入曲线点60.curvePoint.push_back(tempP);61.}62.}63.}64.//三次贝塞尔曲线65.float bezier3funcX(float uu,CvPoint *controlP){66.float part0 = controlP[0].x * uu * uu * uu;67.float part1 = 3 * controlP[1].x * uu * uu * (1 - uu);68.float part2 = 3 * controlP[2].x * uu * (1 - uu) * (1 - uu);69.float part3 = controlP[3].x * (1 - uu) * (1 - uu) * (1 - uu) ;70.return part0 + part1 + part2 + part3;71.}72.float bezier3funcY(float uu,CvPoint *controlP){73.float part0 = controlP[0].y * uu * uu * uu;74.float part1 = 3 * controlP[1].y * uu * uu * (1 - uu);75.float part2 = 3 * controlP[2].y * uu * (1 - uu) * (1 - uu);76.float part3 = controlP[3].y * (1 - uu) * (1 - uu) * (1 - uu) ;77.return part0 + part1 + part2 + part3;78.}翻译] AGG 之贝塞尔插值文章分类:综合技术原文地址：/research/bezier_interpolation/index.html#PAGE_BEZIER_INTERPOLATI ONInterpolation with Bezier Curves 贝塞尔插值A very simple method of smoothing polygons 一种非常简单的多边形平滑方法翻译：唐风之前 comp.graphic.algorithms 上有一个讨论，是关于怎么样使用曲线对多边形进行插值处理，使得最终产生的曲线是光滑的而且能通过所有的顶点。

Bezier曲线原理及实现代码（c++）一、原理：贝塞尔曲线于1962年，由法国工程师皮埃尔·贝塞尔（Pierre Bézier）所广泛发表，他运用贝塞尔曲线来为汽车的主体进行设计。

贝塞尔曲线最初由Paul de Casteljau于1959年运用de Casteljau 算法开发，以稳定数值的方法求出贝塞尔曲线。

线性贝塞尔曲线给定点P0、P1，线性贝塞尔曲线只是一条两点之间的直线。

这条线由下式给出：且其等同于线性插值。

二次方贝塞尔曲线的路径由给定点P0、P1、P2的函数B(t) 追踪：。

TrueType字型就运用了以贝塞尔样条组成的二次贝塞尔曲线。

P0、P1、P2、P3四个点在平面或在三维空间中定义了三次方贝塞尔曲线。

曲线起始于P0走向P1，并从P2的方向来到P3。

一般不会经过P1或P2；这两个点只是在那里提供方向资讯。

P0和P1之间的间距，决定了曲线在转而趋进P3之前，走向P2方向的“长度有多长”。

曲线的参数形式为：。

现代的成象系统，如PostScript、Asymptote和Metafont，运用了以贝塞尔样条组成的三次贝塞尔曲线，用来描绘曲线轮廓。

一般化P0、P1、…、P n，其贝塞尔曲线即。

例如：。

如上公式可如下递归表达：用表示由点P0、P1、…、P n所决定的贝塞尔曲线。

则用平常话来说，阶贝塞尔曲线之间的插值。

一些关于参数曲线的术语，有即多项式又称作n阶的伯恩斯坦基底多项式，定义00 = 1。

点P i称作贝塞尔曲线的控制点。

多边形以带有线的贝塞尔点连接而成，起始于P0并以P n终止，称作贝塞尔多边形（或控制多边形）。

贝塞尔多边形的凸包（convex hull）包含有贝塞尔曲线。

线性贝塞尔曲线函数中的 t 会经过由 P 0 至P 1 的 B(t ) 所描述的曲线。

例如当 t=0.25 时，B(t ) 即一条由点 P 0 至 P 1 路径的四分之一处。

就像由 0 至 1 的连续 t ，B(t ) 描述一条由 P 0 至 P 1 的直线。

作业三：三次Bezier曲线1. 设计要求:1．在程序窗口中建立坐标系2．输入控制点，绘制出三次Ｂｅｚｉｅｒ曲线3．四个控制点间依次用细线连接4．在程序窗口显示四个控制点的位置并标出2. 设计思路:先在草稿纸上算出三次Ｂｅｚｉｅｒ曲线的函数表达式： （０≤ｕ≤１）＝ａ×＋ｂ×＋ｃ×ｕ＋ｄ其中ａ、ｂ、ｃ、ｄ的值为：ａ＝（-） + 3 × - 3 × +ｂ＝3× - 6 × + 3 ×ｃ＝（-3） × + 3 ×ｄ＝将、、、中的（ｘ，ｙ）坐标值分别代入ａ、ｂ、ｃ、ｄ中得到、、、和、、、则：＝×＋×＋×ｕ＋ （１）＝×＋×＋×ｕ＋ （２）根据以上结果（１）和（２）编程求得当ｕ取不同值时所得到的点Ｐ（ｕ）。

再将各点用线连接起来即可拟合三次Ｂｅｚｉｅｒ曲。

3. 设计过程:以下是用ＶＢ编三次Ｂｅｚｉｅｒ曲线时的源代码：其中显示四个控制点的思路是将控制点在ｘ和ｙ方向的坐标值都增大１，然后再与控制点用粗实线连接起来。

这样一来在窗口中显示的即为一个较大的实点。

Function drawcs() '此模块为建立坐标系Dim k As IntegerPictDraw.DrawWidth = 1: PictDraw.FontSize = 9 '设置线宽和字体 PictDraw.Line (-400, 0)-(400, 0), RGB(100, 100, 100)PictDraw.Line (0, -300)-(0, 300), RGB(100, 100, 100)For k = (-360) To 360 Step 40PictDraw.Line (k, -5)-(k, 0): PictDraw.CurrentX = k - 20: PictDraw.CurrentY = 5: PictDraw.Print kNext kFor k = (-280) To -40 Step 40PictDraw.Line (5, k)-(0, k): PictDraw.CurrentX = -40: PictDraw.CurrentY = k - 10: PictDraw.Print (-1) * kNext kFor k = (40) To 280 Step 40PictDraw.Line (5, k)-(0, k): PictDraw.CurrentX = -40: PictDraw.CurrentY = k - 10: PictDraw.Print (-1) * kNext kEnd FunctionPrivate Sub Form_Load()PictDraw.AutoRedraw = TruePictDraw.ScaleWidth = 800PictDraw.ScaleHeight = 600Text1.Text = -300: Text2.Text = -250: Text3.Text = 300: Text4.Text = -250Text5.Text = -300: Text6.Text = 250: Text7.Text = 300: Text8.Text = 250 '作为初始值，便于测试drawcsEnd SubPrivate Sub cmdCancle_Click()PictDraw.Clsdrawcs '清除屏幕后，重建坐标系End SubPrivate Sub delet_Click() '此模块为清除输入框中的值 Text1.Text = ""Text2.Text = ""Text3.Text = ""Text4.Text = ""Text5.Text = ""Text6.Text = ""Text7.Text = ""Text8.Text = ""End SubPrivate Sub cmdDraw_Click() '此模块为画三次Bezier曲线Dim px(4) As Double '定义控制点的x坐标的数组Dim py(4) As Double '定义控制点的y坐标的数组Dim a1, b1, c1, d1 As Double '定义x系数Dim a2, b2, c2, d2 As Double '定义y系数Dim x, y, u As Double '定义曲线中的自变量u和变量x，y Dim i As IntegerIf (Not IsNumeric(Text1) Or Not IsNumeric(Text2) Or Not IsNumeric(Text3) Or Not IsNumeric(Text4) _Or Not IsNumeric(Text5) Or Not IsNumeric(Text6) Or Not IsNumeric(Text7) Or Not IsNumeric(Text8)) ThenText1.Text = "": Text2.Text = ""Text3.Text = "": Text4.Text = ""Text5.Text = "": Text6.Text = ""Text7.Text = "": Text8.Text = ""Text1.SetFocus '判断输入框中的字符是否为数字，如果为数字执行else开始画图Elsepx(0) = Text1.Text: py(0) = Text2.Textpx(1) = Text3.Text: py(1) = Text4.Textpx(2) = Text5.Text: py(2) = Text6.Textpx(3) = Text7.Text: py(3) = Text8.TextPictDraw.FontSize = 18 '设置字体，为显示输入的四个点设置字体大小PictDraw.CurrentX = px(0): PictDraw.CurrentY = (-1) * py(0): PictDraw.Print "P"; 0For i = 0 To 2PictDraw.DrawWidth = 1PictDraw.Line (px(i), (-1) * py(i))-(px(i + 1), (-1) * py(i + 1)), RGB(0, 0, 255): PictDraw.Print "P"; i + 1Next iFor i = 0 To 3PictDraw.DrawWidth = 7PictDraw.Line (px(i), (-1) * py(i))-(px(i) + 1, (-1) * py(i) - 1)Next ia1 = -px(0) + 3 * px(1) - 3 * px(2) + px(3) '计算x和y的参数 b1 = 3 * px(0) - 6 * px(1) + 3 * px(2)c1 = -3 * px(0) + 3 * px(1)d1 = px(0)a2 = -py(0) + 3 * py(1) - 3 * py(2) + py(3)b2 = 3 * py(0) - 6 * py(1) + 3 * py(2)c2 = -3 * py(0) + 3 * py(1)d2 = py(0)For u = 0 To 1 Step 0.001 '每当u增加0.001求一次x和y x = a1 * u * u * u + b1 * u * u + c1 * u + d1 '求x的值y = (-1) * (a2 * u * u * u + b2 * u * u + c2 * u + d2) '求y的值 If u = 0 ThenPictDraw.CurrentX = x '设置画线起点PictDraw.CurrentY = yElsePictDraw.DrawWidth = 2PictDraw.Line -(x, y), RGB(255, 0, 0) '连点成线End IfNext uEnd IfEnd SubPrivate Sub cmdEnd_Click() '退出窗口程序EndEnd Sub4. 设计截图:图四．三次Ｂｅｚｉｅｒ曲线截图。

集美大学计算机工程学院实验报告课程名称计算机图形学教程实验名称实验五、编程生成“三次贝塞尔”曲线实验类型设计型姓名学号日期12月12日地点成绩教师实验目的：一方面，让学生对自由曲线的生成算法有更深入的理解，特别是对于曲线的逼近，能够通过实验编程来验证书上所提供的算法思想：另一方面，在图形程序设计方法（如设计各种各样的图形）、绘图函数的使用以及C和C++语言编程环境、程序的调试和测试方面受到比较系统和严格的训练。

一、实验内容：运用所学的三次贝塞尔曲线生成的算法，根据以下数据点[x, y]：[50, 100] [80, 230] [100, 270] [140, 160] [180, 50] [240, 65] [270, 120] [330, 230] [380, 230] [430, 150]计算出结果，并实现三段贝塞尔在屏幕上显示的功能二、实验要求：（1）3段三次贝塞尔曲线在衔接点上要连续，曲线整体效果要光滑。

（2）整个图形轮廓要清晰，色彩要分明四、实验环境：1．PC，CPU：P4 2.0GHz以上，内存：512M，硬盘：40GB以上；2．操作系统：Microsoft Windows 2000 /2003/XP；3．软件：VC或JAVA等。

五、实验内容及完成情况：#include "graphics.h"#include "conio.h"#include "stdio.h"typedef struct{double x,y;} DPOINT; //定义结构体class Bezier //定义Bezier类{private:DPOINT* bP;int m_maxIndex;void drawFrame();void drawCurve();void drawCurve(int p0,int p1,int p2,int p3);public:Bezier(DPOINT* p,int len); //定义构造函数void draw();};Bezier::Bezier(DPOINT* p,int len) //构造函数的实现{this ->bP=p;m_maxIndex=len-1;}void Bezier::draw() //通过公有函数调用私有函数{drawFrame();drawCurve();}void Bezier::drawFrame() //其功能是绘制出多边形和各个端点{setcolor(12);for(int i=0;i<m_maxIndex;i++){line( bP[i].x, bP[i].y, bP[i+1].x, bP[i+1].y ); //绘制多边形circle(bP[i].x, bP[i].y,5); //绘制各个端点}circle(bP[m_maxIndex].x,bP[m_maxIndex].y,5);}void Bezier::drawCurve() //实现多段Bezier曲线绘制的功能{for(int i=0;i<=m_maxIndex-3;i+=3){drawCurve(i,i+1,i+2,i+3);}}void Bezier::drawCurve(int p0,int p1,int p2,int p3) //实现绘制某一段Bezier曲线的功能{double tmpx=0.0;double tmpy=0.0;double t=0.0;for(;t<=1.0;t+=0.001){tmpx=(-bP[p0].x+3*bP[p1].x-3*bP[p2].x+bP[p3].x)*t*t* t+(3*bP[p0].x-6*bP[p1].x+3*bP[p2].x)*t*t+(-3*bP[p0].x+ 3*bP[p1].x)*t+bP[p0].x;tmpy=(-bP[p0].y+3*bP[p1].y-3*bP[p2].y+bP[p3].y)*t*t* t+(3*bP[p0].y-6*bP[p1].y+3*bP[p2].y)*t*t+(-3*bP[p0].y+ 3*bP[p1].y)*t+bP[p0].y;putpixel(tmpx,tmpy,3);}}void main() //主函数的实现int graphdriver=DETECT,graphmode;initgraph(&graphdriver,&graphmode,"E:\\tc3\\bgi");setbkcolor(0);outtextxy(10,20,"n\n\n\n\n\n\ jisuan1013 2010810070 chengaowei");DPOINT* p;p=new DPOINT[10];p[0].x=50.0;p[0].y=100.0;p[1].x=80.0;p[1].y=230.0;p[2].x=100.0;p[2].y=270.0;p[3].x=140.0;p[3].y=160.0;p[4].x=180.0;p[4].y=50.0;p[5].x=240.0;p[5].y=65.0;p[6].x=270.0;p[6].y=120.0;p[7].x=330.0;p[7].y=230.0;p[8].x=380.0;p[8].y=230.0;p[9].x=430.0;p[9].y=150.0;Bezier bzr(p,10);bzr.draw();delete p;getch(); closegraph();}运行结果：六、实验总结：通过这次实验，让我对自由曲线的生成算法有更深入的理解，特别是对于曲线的逼近，能够通过实验编程来验证书上所提供的算法思想，在图形程序设计方法（如设计各种各样的图形）、绘图函数的使用以及C和C++语言编程环境、程序的调试和测试方面受到比较系统和严格的训练。

bezier曲线代码实现一、什么是贝塞尔曲线？贝塞尔曲线是一种数学曲线，它使用一组控制点来定义一条曲线。

它在计算机图形学、汽车设计和电子游戏等领域得到了广泛的应用。

二、贝塞尔曲线的类型1. 二次贝塞尔曲线：由三个点定义，包括起始点、控制点和结束点。

2. 三次贝塞尔曲线：由四个点定义，包括起始点、两个控制点和结束点。

三、贝塞尔曲线的实现1. 二次贝塞尔曲线的实现：```pythonimport pygamedef quadratic_bezier(points, num_divisions):x0, y0 = points[0]x1, y1 = points[1]x2, y2 = points[2]for i in range(num_divisions):t = i / num_divisionsx = (1 - t)**2 * x0 + 2 * (1 - t) * t * x1 + t**2 * x2y = (1 - t)**2 * y0 + 2 * (1 - t) * t * y1 + t**2 * y2pygame.draw.line(screen, (255, 255, 255), (x, y), (x, y))```2. 三次贝塞尔曲线的实现：```pythonimport pygamedef cubic_bezier(points, num_divisions):x0, y0 = points[0]x1, y1 = points[1]x2, y2 = points[2]x3, y3 = points[3]for i in range(num_divisions):t = i / num_divisionsx = (1 - t)**3 * x0 + 3 * (1 - t)**2 * t * x1 + 3 * (1 - t) * t**2 * x2 + t**3 * x3y = (1 - t)**3 * y0 + 3 * (1 - t)**2 * t * y1 + 3 * (1 - t) * t**2 * y2 + t**3 * y3pygame.draw.line(screen, (255, 255, 255), (x, y), (x, y))```四、总结贝塞尔曲线是一种非常有用的数学工具，它可以被用于多种领域。

三阶贝塞尔曲线伪代码
贝塞尔曲线是一种数学曲线，它在计算机图形学中有着广泛的应用。

三阶贝塞尔曲线（也称为三次贝塞尔曲线）是一种特殊的贝塞尔曲线，它的定义需要三个控制点。

以下是一个伪代码的例子，用于计算三阶贝塞尔曲线上的点：
```plaintext
输入: 控制点 P0, P1, P2 和 P3
输入: 参数 t (0 <= t <= 1)
输出: 曲线上的点 P
P = (1-t)^3 * P0 + 3*(1-t)^2 * t * P1 + 3*(1-t) * t^2 * P2 + t^3 * P3
```
这个伪代码表示的是三阶贝塞尔曲线的参数方程。

给定一个参数`t`，这个方程可以计算出曲线上的一个点 `P`。

`P0`, `P1`, `P2`, 和`P3` 是定义曲线的四个控制点。

这个方程实际上是贝塞尔曲线的基函数的一个线性组合，基函数是 `(1-t)^3`, `3*(1-t)^2 * t`, `3*(1-t) * t^2`, 和 `t^3`。

注意：在实际的编程实现中，你需要确保参数 `t` 的值在 [0, 1] 的范围内，否则结果可能不正确。

你可以使用一些方法（如二分法）来找到这个范围内的 `t` 值。

文章标题：深入探讨JavaScript语言中三次贝塞尔曲线绘制心形代码在本文中，我将深入探讨JavaScript语言中三次贝塞尔曲线绘制心形代码，并通过从简到繁的方式来解析这一主题。

从基础概念入手，逐步深入，帮助您全面、深刻地理解这一主题。

1. 三次贝塞尔曲线简介三次贝塞尔曲线是指在平面上由两个端点和两个中间控制点来定义的二次曲线。

它是一种常用的曲线绘制方法，在JavaScript中，可以通过Canvas来实现对三次贝塞尔曲线的绘制。

在心形代码中，我们将会使用三次贝塞尔曲线来绘制心形的形状。

2. JavaScript Canvas基础在开始讨论三次贝塞尔曲线之前，我们首先需要了解一些JavaScript Canvas的基础知识。

Canvas是HTML5中新增的元素，可用于通过脚本(通常是JavaScript)绘制图形。

使用Canvas，我们可以在网页上绘制出各种图形、动画等。

在心形代码中，我们将通过Canvas来实现三次贝塞尔曲线的绘制。

3. 绘制三次贝塞尔曲线现在，让我们来讨论如何在JavaScript中绘制三次贝塞尔曲线。

在Canvas中，我们可以使用`bezierCurveTo()`方法来绘制三次贝塞尔曲线。

这个方法接受四个参数，分别是两个控制点和一个结束点的坐标。

通过多次调用`bezierCurveTo()`方法，我们可以绘制出复杂的曲线形状。

在心形代码中，我们将会利用这个方法来绘制出心形的形状。

4. 实现心形代码通过以上的基础知识，我们现在可以着手实现JavaScript中绘制心形的代码了。

我们需要定义好心形的各个点的坐标，然后利用`bezierCurveTo()`方法来绘制出心形的形状。

在实现代码的过程中，我们需要仔细考虑控制点的位置和曲线的弧度，以确保绘制出符合预期的心形效果。

5. 个人观点和理解在学习并实践了JavaScript语言中三次贝塞尔曲线绘制心形代码之后，我对这一主题有了更深入的理解。