MATLAB软件入门 第一次数学实验

MATLAB第一次实验报告1. 编程实现以下数列的图像，用户能输入不同的初始值以及系数。

并以x，y为坐标显示图像x(n+1) = a*x(n)-b*(y(n)-x(n)^2);y(n+1) = b*x(n)+a*(y(n)-x(n)^2)程序：function [y1,y2]=draw(a,b,c,x1,y1)x=[];y=[];x(1)=x1;y(1)=y1;n=c;for i=1:nx(i+1)=a*x(i)-b*(y(i)-x(i)^2);y(i+1)=b*x(i)+a*(y(i)-x(i)^2);endy1=x;y2=y;plot(y1,y2)输入：draw（5,1,1,1,2）2. 编程实现奥运5环图，允许用户输入环的直径。

程序：clcclearr=input('input a mnmber:')color1=['b','k','r'];color2=['y','g'];t=linspace(0,2*pi);a1=r+0.2*r;a2=3*r+0.4*r;a3=5*r+0.6*r;a=[a1,a2,a3];b1=2*r+0.3*r;b2=4*r+0.5*r;b=[b1,b2];for i=1:3x=r*cos(t)+a(i);y=r*sin(t);plot(x,y,color1(i),'linewidth',5) axis([0,7*r,-2*r,1.5*r]);hold onaxis equalendfor n=1:2x=r*cos(t)+b(n);y=r*sin(t)-r;plot(x,y,color2(n),'linewidth',5) hold onendaxis off输入：6（圆的半径）3. 实现对输入任意长度向量元素的冒泡排序的升序排列。

不允许使用sort函数。

第一次数学实验报告Matlab基础知识（《数学实验》报告实验名称 Matlab基础知识一、二、PPPPP三、Pexp(PA=[B=[C=A*BD=A.*BPA=[B=[C=(A>B)D=(A==B)E=(A<B)F=(A==B)&(A<B) 2G=(A==B)&(A>B) P sum=0;n=whilen=-n;endpi=Pfor i=x=x*sym(i);endx四、 PPPPP4五、5生验报学实告了解插值与拟合的基本原理和方法；掌握用MATLAB计算插值与作最小二乘多项式拟合和曲线拟合的方法；通过范例展现求解实际微分问题的初步建模过程；通过动手作实验学习如何用插值与拟合方法解决实际问题，提高探索和解决问题的能力。

高中学生这对于学生深入概括数学概念，掌握数学的思维方法，熟悉处理大量的工程计算问题的方法具有十分重要的意义。

二、实验仪器、设备或软件：电脑,MATLAB软件三、实验内容四、实验步骤五、实验要求与任务根据光谱分析内容和步骤，完成以下前述实验，要求写出实验报告（实验目的→问题→数学模型→算法与编程→计算结果→分析、检验和结论→心得体会）。

地球由此推测何时金星与地球的距离（米）的对数值为解：输入命令days=[distancelogs=[tt计算结果：tttt%三次插值综上所得，可推断（（（（解：程序：%输入插值基点数据y=[z=[z=-z;%在矩形区域（7cx=7cy=-cz=griddata(x,y,z,cx,cy','cubic');%作海底曲面图subplot(xlabel('x'),ylabel('y'),zlabel('z')%作出水深小于subplot(clabel(c,h,-插值后作出的海底曲面图及等高线图如下：若船的吃水深度为tv(t)?V?(V?V0)e?，其中V0是电容器的换句话说电压，?是充电常数。

实验一 数学模型的MatlAB 描述一、MatlAB 中数学模型的表示MatlAB 中数学模型的表示主要有三种基本形式：传递函数分子/分母多项式模型、传递函数零极点增益模型和状态空间模型。

它们各有特点，有时需在各种模型之间进行转换。

1. 传递函数分子/分母多项式模型当传递函数为nn n nm m m m a s a sa s ab s b sb sb s G ++++++++=----11101110)(时，在MatlAB 中，直接用分子、分母的系数表示，即],,,[10m b b b num = ],,,[10n a a a d e n = ),()(d e n num tf s G =例1：已知一系统的传递函数2432328()3842ss G s s s s s ++=++++，提取其分子和分母多项式，并绘制零极点图*。

>> num=[3 2 8]; den=[1 3 8 4 2]; G=tf(num,den) [tt,ff]=tfdata(G ,'v') pzmap(G)grid on 结果如下：2. 传递函数的零极点增益模型当传递函数为)())(()())(()(1010n m p s p s p s z s z s z s Ks G ------=时，在MatlAB 中，用[z,p,k]矢量组表示，即[][][]),,()(,,,,,1010k p z zpk s G K k p p p p z z z z n m ====例2:求一传递函数222328()(61)(24)s s G s s s s s ++=++++的零极点及其增益，并绘制零极点图。

>> num=[3 2 8];den=conv([1 6 12],[1 2 4]); G=tf(num,den) GG=zpk(G)[z,p,k]=zpkdata(G ,'v') pzmap(G) grid结果如下：3.状态空间模型当系统的数学模型为状态空间表达式{BuAXX+='+=DuCXY时，在MatlAB中，用[A、B、C、D]矩阵组表示，即系统表示为()DCBAss、、、实验3:已知两系统串联，其中2132265452s sGs s s++=+++，222712432s sGs s++=++，求此串联系统的总的传递函数。

matlab入门实验报告《Matlab入门实验报告》Matlab是一种强大的数学软件，被广泛应用于工程、科学和金融领域。

它具有丰富的功能和灵活的编程语言，适用于数据分析、图形绘制、模型建立等多种应用。

本实验报告将介绍Matlab的基本操作和应用，帮助读者快速入门并掌握基本技能。

首先，我们将介绍Matlab的基本界面和操作方法。

Matlab的界面分为命令窗口、编辑窗口和工作区等部分，用户可以通过命令窗口输入指令进行计算和操作。

编辑窗口则用于编写和编辑Matlab脚本文件，工作区则显示当前的变量和数据。

通过这些基本操作，用户可以快速上手Matlab并进行简单的计算和数据处理。

其次，我们将介绍Matlab的基本数据类型和运算。

Matlab支持多种数据类型，包括数值、字符、逻辑等，用户可以通过简单的指令进行数据的存储和处理。

此外，Matlab还支持各种数学运算和函数，用户可以通过这些函数进行复杂的数学计算和数据分析。

通过实际的例子和练习，读者可以掌握Matlab的基本数据操作和运算方法。

最后，我们将介绍Matlab的图形绘制和数据分析功能。

Matlab提供了丰富的绘图函数和工具，用户可以通过简单的指令绘制各种图形和图表。

同时，Matlab还提供了各种数据分析和统计工具，用户可以通过这些工具进行数据的分析和可视化。

通过实际的案例和练习，读者可以掌握Matlab的图形绘制和数据分析技能。

总之，Matlab是一种强大的数学软件，具有丰富的功能和灵活的编程语言，适用于多种应用领域。

通过本实验报告的介绍和练习，读者可以快速入门Matlab 并掌握基本技能，为今后的学习和工作打下坚实的基础。

Matlabe的学习是一个循序渐进的过程，需要不断的实践和练习，相信通过努力，读者一定能够掌握Matlab并运用于实际的工程和科学问题中。

MATLAB实验报告题目：第一次实验报告学生姓名：学院：专业班级：学号：年月MATLAB第一次实验报告————入门第一次上机实验刘老师就MATLAB软件进行了大致的讲解，并讲了如何建立M文件，定义函数数组矩阵，如何绘图。

先就老师讲解及自己学习的情况做汇报。

一、建立M文件<1>M文件建立方法：1. 在MATLAB中，点:File→New →M-file2. 在编辑窗口中输入程序内容3. 点File →Save，存盘，M文件名必须与函数名一致<2>课上实例例：定义函数f(x1,x2)=100(x2-x12)2+(1-x1)2答：建立M文件：fun.mfunction f=fun(x)f=100*(x(2)-x(1)^2)^2+(1-x(1))^2如此便可以直接使用函数fun.m例如计算f(1,2), 只需在MATLAB命令窗口键入命令：x=[1 2]fun(x)得f =100.<3>课下作业题目：有一函数，写一程序,输入自变量的值,输出函数值.解答：建立M文件：zuoye1.mfunction f=zuoye1(x,y)f=x^2+sin(x*y)+2*y命令行输入x=1,y=1zuoye1(x,y)得ans =3.8415经验算答案正确，所以程序正确。

二、定义数组、矩阵<1>说明逗号或空格用于分隔某一行的元素，分号用于区分不同的行. 除了分号，在输入矩阵时，按Enter 键也表示开始新一行. 输入矩阵时，严格要求所有行有相同的列<2>课后作业题目:有一个4x5矩阵,编程求出其最大值及其所处的位置.解答：a=round(10*rand (4,5))[temp I]=max(a)[am II]=max(temp)p=[I(II) II]运行得一随机矩阵a =7 7 7 3 70 8 2 0 38 7 7 1 109 4 0 8 0temp =9 8 7 8 10I =4 2 1 4 3am =10II =5p = 3 5即最大值为10，位置为第三行第五列。

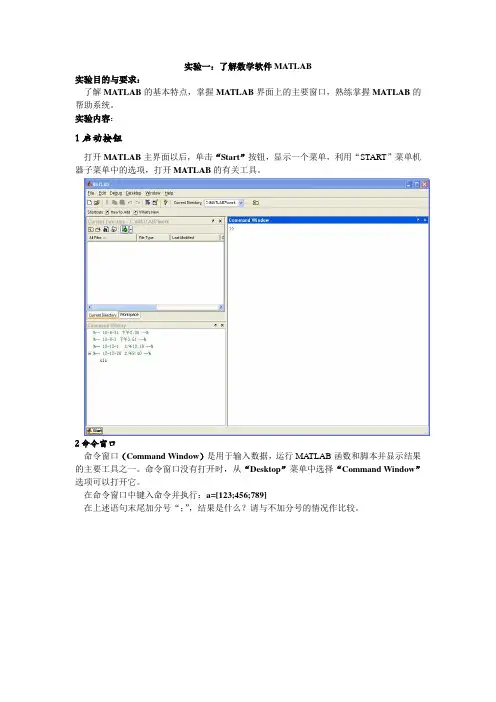
实验一：了解数学软件MATLAB实验目的与要求：了解MATLAB的基本特点，掌握MATLAB界面上的主要窗口，熟练掌握MATLAB的帮助系统。

实验内容：1启动按钮打开MATLAB主界面以后，单击“Start”按钮，显示一个菜单，利用“START”菜单机器子菜单中的选项，打开MATLAB的有关工具。

2命令窗口命令窗口（Command Window）是用于输入数据，运行MA TLAB函数和脚本并显示结果的主要工具之一。

命令窗口没有打开时，从“Desktop”菜单中选择“Command Window”选项可以打开它。

在命令窗口中键入命令并执行：a=[123;456;789]在上述语句末尾加分号“；”，结果是什么？请与不加分号的情况作比较。

功能。

命令历史窗口（command history）显示命令窗口中最近输入的所有语句。

先关闭历史窗口，再分别用“Desktop”菜单打开它和用command history命令打开它。

（1）将命令历史窗口中的语句复制到命令窗口中；（2）直接双击命令历史窗口中的语句。

4工作空间窗口清空工作空间的命令是：clear清空命令窗口的命令是：clc在命令窗口中键入：t=0:pi/4:2*piy=sin(t)在命令窗口中键入：who,看运行结果；在命令窗口中键入：whos,看运行结果；在命令窗口中键入：whos y,看运行结果。

退出MATLAB时，工作空间中的内容随之清除。

可以将当前空间中的部分或全部变量保存到一个MA T文件中，它是一个二进制文件，扩展名为.mat。

然后可以在以后使用它时载入它，请练习这一操作过程。

5帮助浏览器使用帮助浏览器可以搜索和查询所有Math Works产品的文档和演示。

帮助浏览器是集成到MA TLAB桌面的一个HTML查看器。

请打开帮助浏览器，熟悉它。

分别用Help函数和doc函数获取format函数的帮助，进而说明format函数的功能。

实验三图像运算本实验是综合性实验，涵盖Matlab程序设计、代数运算、几何运算等多章基本知识及其应用。

一、实验目的与要求1、理解图像代数运算、几何运算的基本定义和常见方法。

2、掌握在MTLAB中对图像进行代数运算、几何运算的方法。

3、掌握在MATLAB中进行插值的方法。

4、运用MATLAB语言实现图像的插值缩放和插值旋转.二、实验原理代数运算是指对两幅输入图像进行点对点的加、减、乘或除运算而得到输出图像的运算。

对于相加和相乘的情形，可能不止有两幅图像参加运算。

在一般情况下，输入情况之一可能为常数。

四种图像处理代数运算的数学表达式如下：C(x,y)=A(x,y)+B(x,y)C(x,y)=A(x,y)-B(x,y)C(x,y)=A(x,y)*B(x,y)C(x,y)=A(x,y)/B(x,y)其中A(x,y)和B(x,y)为输入图像，而C(x,y)为输出图像。

还可以通过适当的组合形成涉及几幅图像的复合代数运算方程。

在MATLAB中，我们可以用函数简单的得到数字图像的图像数据矩阵（即A(x,y)和B(x,y)），有了这些矩阵后我们只要适当的设计代数运算的形式并写出方程，就可以得到一个输出图像的矩阵（即C(x,y)）图像相加的一个重要应用是对同一场景的多幅图像求平均值。

这点被经常用来有效的降低加性随机噪声的影响。

如果把B（x,y）换成一个常数，通过加、减、乘、除运算可实现图像亮度的调整。

几何运算可改变图像中各物体之间的空间关系。

这种运算可以被看成是将物体在图像内移动。

一个几何运算需要两个独立的算法。

首先，需要一个算法来定义空间变换本身，用它来描述每个像素如何从其初始位置“移动”到终止位置，即每个像素的“运动”。

同时，还需要一个用于灰度插值的算法，这是因为，在一般情况下，输入图像的位置坐标(x,y)为整数，而输出图像的位置坐标为非整数，反过来也如此。

因此插值就是对变换之后的整数坐标位置的像素值进行估计。

初识MATLAB的实验报告1. 引言MATLAB（Matrix Laboratory）是一种高级的技术计算环境和编程语言。

它具有强大的矩阵计算能力和丰富的科学和工程绘图功能，被广泛应用于各个领域的科研与工程实践中。

本实验旨在初步了解MATLAB的基本语法和功能，通过实际操作加深对MATLAB编程的理解。

2. 实验目的1. 掌握MATLAB的安装和基本使用方法；2. 学习MATLAB中的常用数学函数和操作；3. 了解MATLAB绘图功能并能够绘制简单的图形。

3. 实验步骤3.1 MATLAB安装首先，在官方网站（3.2 MATLAB入门3.2.1 MATLAB语法MATLAB的语法类似于其他常见的编程语言，每个语句以分号结尾。

在MATLAB 中，可以直接进行基本的数学运算，例如加减乘除、指数、对数等。

通过以下代码可以计算两个变量的和并将结果打印出来：matlaba = 10;b = 20;sum = a + b;disp(sum);3.2.2 MATLAB变量在MATLAB中，可以创建和操作各种类型的变量，例如数值、字符串、矩阵等。

以下代码演示了如何创建一个矩阵：matlabmatrix = [1, 2, 3; 4, 5, 6; 7, 8, 9];disp(matrix);3.2.3 MATLAB函数MATLAB提供了许多内置的数学函数，可以直接调用。

以下代码演示了如何计算正弦函数值并打印结果：matlabx = pi/4;y = sin(x);disp(y);3.3 MATLAB绘图MATLAB具有强大的绘图功能，可以绘制各种图形，如曲线、散点图、柱状图等。

以下代码演示了如何绘制一个简单的正弦曲线：matlabx = linspace(0, 2*pi, 100);y = sin(x);plot(x, y);xlabel('x');ylabel('y');title('Sine Curve');4. 实验结果与分析在完成上述实验步骤后，我们成功安装了MATLAB，并学习了基本的语法、变量和函数的使用方法。

撰写人姓名： 撰写时间： 审查人姓名：实 验 全 过 程 记 录实验名称 MATLAB 使用入门实验时间 2学时 地点数学实验室姓 名 学 号 班 组 同实验者学 号班 组一、实验目的1、熟悉MATLAB 环境及相应设置；2、熟练掌握MATLAB 编程工具及帮助功能；3、熟练掌握MATLAB 基本数据类型、基本运算、四种流程语句；4、熟练掌握MATLAB 自定义函数方法；5、熟练掌握二维图形科学绘制方法；6、掌握MATLAB 三维图形绘制方法。

二、实验内容：1、学习MATLAB 编程环境；2、针对实际问题利用相应帮助功能学习编程；3、编程基础知识练习，包括基本数据类型、基本运算、流程语句、自定义函数等；4、科学绘制二、三维图形，对基本的绘图选项进行设定。

三、实验用仪器设备及材料软件需求：操作系统：Windows XP 或更新的版本； 实用数学软件：MATLAB 7.0或更新的版本。

硬件需求：Pentium IV 450以上的CPU 处理器、512MB 以上的内存、5000MB 的自由硬盘空间、 CD-ROM 驱动器、打印机、打印纸等。

四、实验原理:线性代数理论及MATLAB 中矩阵的特殊运算规定五、实验步骤：1、熟悉MATLAB 环境及相应设置。

2、分别用help 、lookfor 命令查看log 等函数的帮助信息，掌握函数log 的使用方法，并 比较二命令的不同之处。

3、给定2ln 3x y z x e y x +=+--，在Command Window 中键入相应表达式，并求2x =、4y =时z 的值。

4、在Command Window 中分别利用冒号操作符和linspace 函数生成向量()10,8,,0α= 。

5、已知：422305153A -⎡⎤⎢⎥=-⎢⎥⎢⎥⎣⎦，134203211B ⎡⎤⎢⎥=--⎢⎥-⎢⎥⎣⎦，在Command Window 中建立A 、B 矩阵并对其进行以下操作：1、提取A 的第一行、第三行；2、提取B 的第一列、第二列；3、交换A 的第一行和第二行生成A1，交换B 第一列和第三列生成B1；4、分别从横向和纵向合并A 和B ；5、构建矩阵C ，C 的第一、二行由A 的第一、二行的第一、二列元素构成，C 的第三、四行由B 第二、三行的第二、三列元素构成。

MATLAB数学实验报告姓名：李帆班级：机械（硕）21学号：2120104008第一次数学实验报告——线性规划问题一，实验问题1，某饲养场饲养动物出售，设每头动物每天至少需要700g蛋白质，30g矿物质，100mg 维生素。

现有五种饲料可供选择，各种饲料的每千克营养成分含量和单价如下表。

是确定既能满足动物生长的营养需要，游客是费用最省的选用饲料方案。

2，某工厂生产甲、乙、丙三种产品，单位产品所需工时分别为2、3、1个；单位产品所需原料分别为3、1、5公斤；单位产品利润分别为2、3、5元。

工厂每天可利用的工时为12个，可供应的原料为15公斤。

为使总利润为最大，试确定日生产计划和最大利润。

二，问题分析1，1）该题属于采用线性规划的方式求出最优解的数学问题。

该题有以下特点，1.目标函数有线性，是求目标函数的最小值;2.约束条件为线性方程组；3.未知变量都有非负限制。

1，2）求解该类问题的方法有图解法，理论解法和软件解法。

图解法常用于解变量较少的线性规划问题。

理论解法要构建完整的理论体系。

目前用于解线性规划的理论解法有：单纯形法，椭球算法等。

在此，我们采用单纯形法的MATLAB软件解法来求解该问题。

1，3）此题中，要求既要满足动物生长的营养需要，又要使费用最省，则使每种饲料的选用量为变量，以总费用的最小值为所求量，同时每种饲料的使用量要符合营养成分的要求。

1，4）在此，首先确定建立线性规划模型。

设饲料i选用量为xi公斤，i=1,2,3,4,5.则有模型：Minz=0.2x1+0.7x2+0.4x3+0.3x4+0.8x5s.t. {3x1+2x2+6x4+18x5>=700;x1+0.5x2+0.2x3+2x4+0.5x5>=300.5x1+x2+0.2x3+2x4+0.8x5>=100Xj>=0,j=1,2,3,4,5解之得：x1=x2=x3=0X4=39.74359X5=25.14603Zmin=32.435902, 1）该问题与第一题分析步骤相似，故只在此写出其线性规划模型Z=2x+3y+5z2x+3y+z<=123x+y+5z<=15三，程序设计流程图第一题：c=[0.2,0.7,0.4,0.3,0.8]A=[3,2,1,6,18;1,0.5,0.2,2,0.5;0.5,1,0.2,2,0.8;1,0,0,0,0;0,1 ,0,0,0;0,0,1,0,0;0,0,0,1,0;0,0,0,0,1]b=[700,30,100,0,0,0,0,0][x,fval]=linprog(c,-A,-b)c =0.2000 0.7000 0.4000 0.3000 0.8000A =3.0000 2.0000 1.0000 6.0000 18.00001.0000 0.5000 0.20002.0000 0.50000.5000 1.0000 0.2000 2.0000 0.80001.0000 0 0 0 00 1.0000 0 0 00 0 1.0000 0 00 0 0 1.0000 00 0 0 0 1.0000b =700 30 100 0 0 0 0 0Optimization terminated.x =0.0000-0.00000.000039.743625.6410fval =32.4359第二题c=[-2 -3 -5]A=[2 3 1;3 1 5]b=[12;15]lb=[0 0 0][x,Z,exitflag,output]=linprog(c,A,b,[],[],lb,[])将上述程序输入matlab。

实验一Matlab使用方法和程序设计一、实验目的1、掌握Matlab软件使用的基本方法；2、熟悉Matlab的数据表示、基本运算和程序控制语句3、熟悉Matlab绘图命令及基本绘图控制4、熟悉Matlab程序设计的基本方法二、实验内容：1、帮助命令使用help命令，查找sqrt（开方）函数的使用方法；'解：sqrtSquare rootSyntaxB = sqrt(X)DescriptionB = sqrt(X) returns the square root of each element of the array X. For the elements of X that are negative or complex, sqrt(X) produces complex results.RemarksSee sqrtm for the matrix square root.Examples;sqrt((-2:2)')ans =0 +0 +2、矩阵运算（1）矩阵的乘法/已知A=[1 2;3 4]; B=[5 5;7 8];求A^2*B解：A=[1 2;3 4 ];B=[5 5;7 8 ];A^2*B（2）矩阵除法已知A=[1 2 3;4 5 6;7 8 9]; `B=[1 0 0;0 2 0;0 0 3];A\B,A/B解：A=[1 2 3;4 5 6;7 8 9 ];B=[1 0 0;0 2 0;0 0 3 ];A\B,A/B（3）矩阵的转置及共轭转置已知A=[5+i,2-i,1;6*i,4,9-i];*求A.', A'解：A=[5+1i,2-1i,1;6*1i,4,9-1i ];A1=A.',A2=A'（4）使用冒号表达式选出指定元素已知：A=[1 2 3;4 5 6;7 8 9];<求A中第3列前2个元素；A中所有列第2，3行的元素；方括号[]解：A=[1 2 3;4 5 6;7 8 9 ];B=A([1,2],[3]),C=A(2:end, : )用magic 函数生成一个4阶魔术矩阵，删除该矩阵的第四列'3、多项式（1）求多项式 42)(3--=x x x p 的根解：A=[1 0 -2 -4];B=roots(A)（2）已知A=[ 3 5 ;5 5 6;3 9 0 1;1 2 3 4] ，求矩阵A 的特征多项式;解：/A=[ 3 5 .9 ; 5 5 6 ;3 9 0 1 ;1 2 3 4];A=poly(A);A=poly2sym(A)把矩阵A作为未知数代入到多项式中；4、基本绘图命令（1）绘制余弦曲线y=cos(t)，t∈[0，2π]解：t=0:.1:2*pi;y=cos(t);plot(t,y),grid~（2）在同一坐标系中绘制余弦曲线y=cos和正弦曲线y=sin，t∈[0，2π] t=0:.1:2*pi; y1=cos;y2=sin;plot(t,y1，t,y2)grid》5、基本绘图控制绘制[0，4π]区间上的x1=10sint曲线，并要求：（1）线形为点划线、颜色为红色、数据点标记为加号；（2）坐标轴控制：显示范围、刻度线、比例、网络线（3）标注控制：坐标轴名称、标题、相应文本；t=0:.01:4*pi;y=10*sin(t);plot(t,y,'-.',t,y,'r')grid\6、基本程序设计（1）编写命令文件：计算1+2+…+n<2000 时的最大n值；解法1：s=0;i=0;while(s<2000) i=i+1;s=s+i; ends=s-i,i=i-1解法2：s=0;for i=1:1000; s=s+i;if(s>2000) ,break;endend；s=s-i,i=i-1（2）编写函数文件：分别用for和while循环结构编写程序，求2的0到n次幂的和。

实验一MATLAB环境的熟悉与数值计算一、实验目的：1．熟悉MATLAB开发环境；2．掌握矩阵、数组、关系和逻辑的各种基本运算；3．掌握矩阵的分解和多项式的创建；4．掌握基本数据分析的函数应用。

二、实验器材：计算机，MATLAB运行环境。

三、实验基本知识：1.熟悉MATLAB环境:MATLAB桌面和命令窗口、命令历史窗口、帮助信息浏览器、工作空间浏览器文件和搜索路径浏览器。

2.掌握MATLAB常用命令3.MATLAB运算符变量命名规则如下：（1）变量名可以由英语字母、数字和下划线组成（2）变量名应以英文字母开头（3）长度不大于31个（4）区分大小写MATLAB运算符，通过下面几个表来说明MATLAB的各种常用运算符表3 MATLAB关系运算符表4 MATLAB逻辑运算符表5 MATLAB特殊运算4.MATLAB的一维、二维数组的寻访表6 子数组访问与赋值常用的相关指令格式5.MATLAB的基本运算表7 两种运算指令形式和实质内涵的异同表6.MATLAB的常用函数表8 标准数组生成函数表9 数组操作函数7. 矩阵运算：矩阵加、减（＋,－）运算矩阵乘（*）运算矩阵乘方inv ——矩阵求逆det ——行列式的值eig ——矩阵的特征值diag ——对角矩阵‟ ——矩阵转置sqrt ——矩阵开方8. 矩阵的数组运算：数组加减(.+,.-)：对应元素相加减数组乘(.*）：a，b两数组必须有相同的行和列，两数组相应元素相乘数组除（./，.\）：a./b=b.\a —都是b的元素被a的对应元素除（a除以b）a.\b=b./a —都是a的元素被b的对应元素除（除以a）数组乘方(.^)：元素对元素的幂数组点积（点乘）：维数相同的两个向量的点乘，其结果是一个标量数组叉积：就是一个过两个相交向量的交点且垂直于两个向量所在平面的向量数组混合积:先叉乘后点乘9. 多项式运算poly ——产生特征多项式系数向量roots ——求多项式的根p=poly2str(c,…x‟)（以习惯方式显示多项式）四、实验内容五、实验报告要求：1、简述实验目的、实验原理、实验内容和实验过程2、总结实验中的主要结论、实践技能和心得体会3、附上实验过程中所用的程序实验二MATLAB符号处理与绘图一、实验目的：1. 掌握创建符号变量、符号表达式、符号矩阵的创建方法；2. 掌握符号矩阵与数值矩阵的转换方法；3. 掌握符号矩阵运算；4. 掌握字符串的比较方法；5. 掌握二维图形的基本绘制方法；6. 掌握三维图形的基本绘制方法；7. 掌握常用图形处理方法。

实验一 MATLAB软件初步1.1实验目的在计算机上进行数学实验需要一个功能完备的计算平台，本数学实验系列课程均在MATLAB软件环境中进行数学实验。

而本实验的目的就是熟悉MATLAB软件使用环境，并掌握其基本应用，为后续实验课程奠定必要的计算机基础。

1.2 实验要求本实验要求学生掌握MATLAB软件的基本功能，会使用MATLAB进行简单的数值运算，会使用plot函数绘制简单二维图形，会编写简单的MATLAB程序，会使用常用MATLAB帮助命令。

1.3知识概要1.3.1 导言MATLAB是 MATrix LABoratory 的缩写，是由美国MathWorks公司开发的工程计算软件。

MATLAB语言是以数组为基本数据单位，包括控制流程语句、函数、数据结构、输入输出及面向对象等特点的高级语言，具有以下主要特点：1）运算符和库函数极其丰富，语言简洁，编程效率高。

MATLAB除了提供和C语言一样的运算符外，还提供广泛的矩阵和向量运算符。

2）既具有结构化的控制语句（如for循环、while循环、break语句、if语句和switch语句），又有面向对象的编程特性。

3）图形功能强大。

它既包括对二维和三维数据可视化、图像处理、动画制作等高层次的绘图命令，也包括可以完全修改图形局部及编制完整图形界面的、低层次的绘图命令。

1.3.2 MATLAB软件环境启动MATLAB后，软件界面如下图所示，该界面主要包括命令窗口、工作区窗口、历史命令窗口、当前目录窗口。

图 1 MATLAB 主窗口1 命令窗口(Command Window)命令窗口是用户与MATLAB 进行交互的主要场所，命令窗口的空白区域，用于输入和显示计算结果，可以在该区域键入各种MATLAB 命令进行各种操作，键入数学表达式进行计算。

例如，当键入变量赋值命令：123x =+⨯，并回车, 将在命令行的下面显示：再输入求三角正弦函数值的表达式sin()4y =并回车，将显示：在进行程序设计时，首先需要对变量进行命名，MATLAB的变量名称需要符合以下规则：⏹以字母开头，后面可跟字母，数字和下短线；⏹大小写字母有区别；⏹不超过31个字符。

《用MATLA描述常用信号及信号运算》
实
验
报
告
班级:
学号:
姓名:
实验时间：
主讲教师：
1、连续信号
2、离散信号
1、连续信号
2、离散信号
答：一般来说，因为我们目前使用的计算机是0101的数字化系统，它的处理过程也是离散数学的领域。

MATLAB正是处理计算机0101数字化系统的，同时MATLAB处理的是矩阵，它的处理过程是离散数学的领域。

将连续信号进行离散化处理之后，得到的是一个0101数字化的矩阵，使得MATLAB能够处理这样的离散信号。

同时，离散化之后的的信号任然适合密集的，将众多个密集的点聚集在一起也可以视作连续的信号。

华北水利水电大学信息工程学院Matlab实验报告学号：201215828姓名：谭秋教师：陈黎霞实验1.基本操作命令练习一、实验目的1.熟悉matlab软件及基本操作命令；2.通过实验掌握矩阵的建立方法；二、实验环境1.计算机2.matlab软件三、实验说明1.熟悉matlab运行环境，正确操作，认真观察；2.实验学时：2学时；3.整理实验结果，提交实验报告。

四、实验内容1.熟悉(1)命令窗口的使用；(2)工作空间窗口的使用；(3)工作目录、搜索路径的设置；(4)命令历史记录窗口的使用；(5)各菜单及帮助系统的使用。

2.练习常用的键盘操作和快捷键4. (1)输入 A=[7 1 5；2 5 6；3 1 5]，B=[1 1 1; 2 2 2; 3 3 3]，在MATLAB中可以得到A，B两个矩阵。

如下图所示：在命令窗口中执行下列表达式，掌握其含义：A(2, 3) ， A(:,2) ，A(3,:) ， A(:,1:2:3) ， A(:,3).*B(:,2)，A(:,3)*B(2,:)，A(2, 3)表示A矩阵里边第二行第三列的元素；A(:,2)表示A矩阵里边第二列的元素；A(3,:)表示A矩阵里边第三行的元素；A(:,1:2:3)表示A矩阵里边按列取，取第一列和第三列的元素；A(:,3).*B(:,2)表示A矩阵里边的第三列元素和B矩阵里边第二列元素的点运算。

A(:,3)*B(2,:)表示A矩阵里边的第三列元素和B矩阵里边的第二列元素的矩阵运算。

(2)输入 C=1:2:20，则C（i）表示什么？其中 i=1,2,3, (10)答：输入 C=1:2:20，则C（i）表示在1到20之间从1开始取数，且每个数相差2，到20截止。

如下图所示。

（3）保存变量 C 到指定路径下；删除workspace中的C，重新加载C。

答：点击save workspace,将变量C保存到本地磁盘D:\ matlab\ bin 里边，并且命名为matlab变量C.m。

MATLAB软件与基础数学实验Saw H.Z实验1 MATLAB基本特性与基本运算例1-1求[12+2×(7-4)]÷32的算术运算结果。

>> clear>> s=(12+2*(7-4))/3^2s =2例1-2计算5!，并把运算结果赋给变量yy=1;for i=1:5y=y*i;endy例1-3计算2开平方>> s=2^(0.5)s =1.4142>>例1-4 计算2开平方并赋值给变量x（不显示）查看x的赋值情况a=2;x=a^(0.5);x例1-4设75,24=-=ba，计算|)tan(||)||sin(|baba++的值。

a=(-24)/180*pi; b=75/180*pi; a1=abs(a);b1=abs(b);c=abs(a+b);s=sin(a1+b1)/(tan(c))^(0.5)例1-5 设三角形三边长为2,3,4===c b a ，求此三角形的面积。

a=4;b=3;c=2; p=(a+b+c)/2;s=(p*(p-a)*(p-b)*(p-c))^(0.5)例1-7 设⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=101654321A ，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=112311021B ，计算||,,A AB B A +，1-A 。

a=[1,2,3;4,5,6;1,0,1];b=[-1,2,0;1,1,3;2,1,1]; x=a+b; y=a*b; z=norm(a); q=inv(a); x,y,z,q例1-8 显示上例中矩阵A 的第2行第3列元素，并对其进行修改. a=[1,2,3;4,5,6;1,0,1];x=a(2,3);a(2,3)=input('change into=') x,a例1-9 分别画出函数x x y cos 2=和x xz sin =在区间[-6π,6π]上的图形。

a=1;x=-1/6*pi:0.01:1/6*pi; y=(x.*x).*cos(x); z=sin(x)/x; plot(x,y,x,z);例1-10 试求方程组⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--432201624121X 的解。