2014年 北京四中 高三数学高考总复习:15 导数的综合应用 (理) 配套相应练习与解析(基础)巩固练习
- 格式:doc
- 大小:642.50 KB
- 文档页数:6

函数的基本性质(提高)【考纲要求】1. 了解函数的定义域、值域,并能简单求解.2. 理解函数的单调性、最大(小)值及其几何意义;结合具体函数,了解函数奇偶性的含义.3. 会运用函数图象理解和研究函数的性质. 【知识网络】【考点梳理】1.单调性(1)一般地,设函数()f x 的定义域为I 如果对于定义域I 内某个区间D 上的任意两个自变量的值12,x x ,当12x x <时,若都有12()()f x f x <,那么就说函数在区间D 上单调递增,若都有12()()f x f x >,那么就说函数在区间D 上单调递减。
(2)如果函数()y f x =在区间D 上是增函数或减函数,那么就说函数()y f x =在这一区间具有严格的单调性,区间D 叫做()y f x =的单调区间。
(3)判断证明函数单调性的一般方法:单调四法,导数定义复合图像 定义法:用定义法证明函数的单调性的一般步骤是①设D x x ∈21,,且12x x <;②作差)()(21x f x f -;③变形(合并同类项、通分、分解因式、配方等)④判断)()(21x f x f -的正负符号;⑤根据定义下结论。
复合函数分析法设()y f u =,()u g x =[,]x a b ∈,[,]u m n ∈都是单调函数,则[()]y f g x =在[,]a b 上也是单调函数,其单调性由“同增异减”来确定,即“里外”函数增减性相同,复合函数为增函数,“里外”函数的增减性相反,复合函数为减函数。
如下表:()u g x =()y f u =[()]y f g x =增 增 增 增减减函数的基本性质 奇 偶 性单 调 性周 期 性减 增 减 减减 增导数证明法:设()f x 在某个区间(,)a b 内有导数'()f x ,若()f x 在区间(,)a b 内,总有'()0('()0)f x f x ><,则()f x 在区间(,)a b 上为增函数(减函数);反之,若()f x 在区间(,)a b 内为增函数(减函数),则'()0('()0)f x f x ≥≤。

第5讲 导数及其应用【高考考情解读】1.本讲主要考查导数几何意义,导数的四则运算及利用导数研究函数的单调性,求函数的极值、最值等.2.常与直线、圆锥曲线、分式、含参数的一元二次不等式等结合在一起考查,题型多样,属中高档题目.1.导数的几何意义:函数y =f (x )在点x =x 0处的导数值就是曲线y =f (x )在点(x 0,f (x 0))处的切线的斜率,其切线方程是))(()(000x x x f x f y -'=-.(其中斜率)(0'x f k =)2.导数与函数单调性的关系:(1)0)('>x f 是f (x )为增函数的充分不必要条件,如函数f (x )=x 3在(-∞,+∞)上单调递增,但)('x f ≥0. (2))('x f ≥0是f (x )为增函数的必要不充分条件,当函数在某个区间内恒有f ′(x )=0时,则f (x )为常数,函数不具有单调性. 3.函数的极值与最值(1)函数的极值是局部范围内讨论的问题,函数的最值是对整个定义域而言的,是在整个范围内讨论的问题. (2)函数在其定义区间的最大值、最小值最多有一个,而函数的极值可能不止一个,也可能没有.(3)闭区间上连续的函数一定有最值,开区间内的函数不一定有最值,若有唯一的极值,则此极值一定是函数的最值.4.常见的导数公式及两个常用的运算法则(1) 0='C (C 为常数). (2) '1()()n n x nx n Q -=∈. (3) x x cos )(sin ='. (4) x x sin )(cos -='.(5) x x 1)(ln =';e a xx a log 1)(log ='. (6) x x e e =')(; a a a x x ln )(='. (7)2'11x x -=⎪⎭⎫ ⎝⎛(8)()xx 21'= (9)'''()u v u v ±=±. (10)'''()uv u v uv =+. (11)'''2()(0)u u v uv v v v -=≠. 5.定积分的三个公式与一个定理 (1)定积分的性质:①⎰badx x kf )(()bak f x dx =⎰(k 是常数)②[()()]baf xg x dx ±=⎰⎰badx x f )(±⎰badx x g )( ③⎰b adx x f )(⎰=c adx x f )(⎰+bcdx x f )( (其中a <c <b ).(2)微积分基本定理:一般地,如果f (x )是区间[a ,b ]上的连续函数,并且)('x F =f (x ),那么=⎰badx x f )()()(a F b F -。
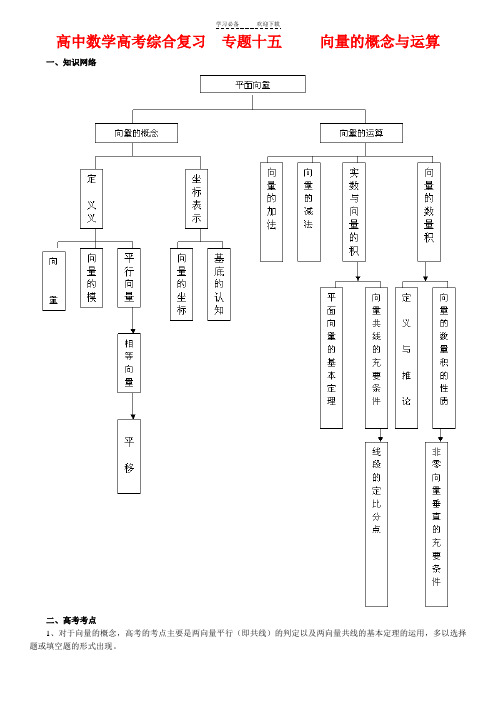
高中数学高考综合复习专题十五向量的概念与运算一、知识网络二、高考考点1、对于向量的概念,高考的考点主要是两向量平行(即共线)的判定以及两向量共线的基本定理的运用,多以选择题或填空题的形式出现。
2、对于向量的运算,向量的数量积及其运算是向量的核心内容,对此,高考的考点主要是:(1)向量的加法、减法的几何意义与坐标表示的应用;(2)向量共线的充要条件的应用;(3)向量垂直的充要条件的应用;(4)向量的夹角的计算与应用;(5)向量的模的计算,关于向量的模的等式的变形与转化,关于向量的模的不等式的认知与转化。
3、线段的定比分点线或平移问题。
4、以向量为载体的三角求值或图象变换问题,以向量为载体的函数或解析几何问题(多以解答题的形式出现)。
三、知识要点(一)向量的概念1、定义(1)向量:既有大小又有方向的量叫做向量。
(2)向量的模:向量的大小(即长度)叫做向量的模,记作。
特例:长度为0的向量叫做零向量,记作;长度为1的向量叫做单位向量.(3)平行向量(共线向量):一般定义:方向相同或相反的非零向量叫做平行向量,平行向量也叫做共线向量.特殊规定:与任一向量平行(即共线).(4)相等向量:长度相等且方向相同的向量叫做相等向量。
零向量与零向量相等。
认知:向量的平移具有“保值性”。
2、向量的坐标表示(1)定义:在直角坐标系内,分别取与x轴、y轴正方向相同的两个单位向量、作为基底,任作一个向量,则由平面向量基本定理知,有且只有一对实数x,y使得,将有序实数对(x,y)叫做向量的坐标,记作;并将叫做向量的坐标表示。
(2)认知:相等的向量,其坐标也相同,反之成立。
(二)向量的运算1、向量的加法2、向量的减法3、实数与向量的积(1)定义(2)实数与向量的积的运算律:(3)平面向量的基本定理:如果是同一面内的两个不共线向量,那么对于这一平面内的任一向量,有且只有一对实数1,2使,这两个不共线的向量叫做表示这一平面内所有向量的一组基底。


"北京市第四中学2014届高三数学总复习导数函数的综合(提高)新人教A版 "1.当x>0时,f(x)=x+的单调递减区间是()。
A、(2, +¥)B、(0,2)C、D、2.设函数f(x)=(x3-1)2+1,下列结论中正确的是()。
A、x=1是函数f(x)的极小值点,x=0是极大值点B、x=1及x=0均是f(x)的极大值点C、函数f(x)至多有一个极大值和一个极小值D、x=1是函数f(x)的极小值点,函数f(x)无极大值点3.函数y=x4-2x2+5, x∈[-2,2]的最大值和最小值分别为()。
A、13,-4B、13,4C、-13,-4D、-13,44.若函数f(x)=x3+ax在R上有两个极值点,则实数a的取值范围是()。
A、a>0B、a<0C、a≥0D、a≤05. 设函数,集合M=,P=,若M P,则实数a的取值范围是 ( )A.(-∞,1)B.(0,1)C.(1,+∞)D. [1,+∞)6.对正整数n,设曲线在x=2处的切线与y轴交点的纵坐标为,则数列的前n项和的公式是______。
7.证明函数在(2,4)上是减函数。
8. 设函数f(x)=2x3+3ax2+3bx+8c在x=1及x=2时取得极值。
(Ⅰ)求a、b的值;(Ⅱ)若对于任意的x∈[0,3],都有f(x)<c2成立,求c的取值范围。
9.做一个容积为256升的方底无盖水箱,问高为多少时最省材料?10.已知f(x)=x3-3bx+36在(0,1)内有极小值,则实数b的取值范围是______;11.设a>0,求函数的单调区间。
12.用总长14.8m的钢条制作一个长方体容器的框架,如果所制作容器的底面的一边比另一边长0.5m,那么高为多少时容器的容积最大?并求出它的最大容积。
13.已知函数,其中a , b , c是以d为公差的等差数列且a>0,d>0.设上,处取得最大值,在,将点依次记为A, B, C(I)求的值;(II)若⊿ABC有一边平行于x轴,且面积为,求a ,d的值。

【巩固练习】1.若()sin cos f x x α=-,则'()f α等于( ) A .sin α B .cos α C .sin cos αα+D .2sin α2.若函数2()f x x bx c =++的图象的顶点在第四象限,则函数'()f x 的图象是( )3.已知函数1)(23--+-=x ax x x f 在),(+∞-∞上是单调函数,则实数a 的取值范围是( )A .),3[]3,(+∞--∞B .]3,3[-C .),3()3,(+∞--∞D .)3,3(-4.对于R 上可导的任意函数()f x ,若满足'(1)()0x f x -≥,则必有( )A . (0)(2)2(1)f f f +< B. (0)(2)2(1)f f f +≤ C.(0)(2)2(1)f f f +≥ D. (0)(2)2(1)f f f +>5.若曲线4y x =的一条切线l 与直线480x y +-=垂直,则l 的方程为( )A .430x y --=B .450x y +-=C .430x y -+=D .430x y ++=6.函数)(x f 的定义域为开区间),(b a ,导函数)(x f '在),(b a 内的图象如图所示,则函数)(x f 在开区间),(b a 内有极小值点( )A .1个B .2个C .3个D .4个7.若函数()()2f x x x c =-在2x =处有极大值,则常数c 的值为_________; 8.函数x x y sin 2+=的单调增区间为 。
9.设函数())(0)f x ϕϕπ=+<<,若()()f x f x '+为奇函数,则ϕ=__________ 10.设321()252f x x x x =--+,当]2,1[-∈x 时,()f x m <恒成立,则实数m 的取值范围为 。
11.对正整数n ,设曲线)1(x x y n -=在2x =处的切线与y 轴交点的纵坐标为n a ,则数列1n a n ⎧⎫⎨⎬+⎩⎭的前n 项和的公式是12.设13()ln 1,22f x a x x x =+++其中a R ∈,曲线()y f x =在点(1,(1))f 处的切线垂直于y 轴. (Ⅰ) 求a 的值;(Ⅱ) 求函数()f x 的极值. 13.设1()(0)xx f x ae b a ae=++> (I)求()f x 在[0,)+∞上的最小值;(II)设曲线()y f x =在点(2,(2))f 的切线方程为32y x =;求,a b 的值. 14.已知函数32()f x x ax bx c =+++在23x =-与1x =时都取得极值 (1)求,a b 的值与函数()f x 的单调区间(2)若对[1,2]x ∈-,不等式2()f x c <恒成立,求c 的取值范围。
高考冲刺:导数与函数的综合【高考展望】1.函数在一点处导数的几何意义、切线的斜率、方程等常作为基础考察;2.基本导数公式,两个函数和、差、积、商的求导法则要熟记并应用, 5.理科试卷中往往考察复合函数的求导法则;6.函数的单调性与其导数的关系,能利用导数研究函数的单调性,此为重点内容,也是重点考察的内容;7.函数在某点取得极值的必要条件和充分条件(导数在极值点两侧异号),函数的极大值、极小值、最大值、最小值是考查重点;8. 正确计算定积分,利用定积分求面积;9.分类讨论的数学思想是本部分内容的重点考查内容,应熟练掌握这种数学思想。
【知识升华】考点一、求切线方程的一般方法,可分两步: (1)求出函数()y f x =在0x x =处的导数0()f x ';(2)利用直线的点斜式得切线方程。
要点诠释:求切线方程,首先要判断所给点是否在曲线上.若在曲线上,可用上法求解;若不在曲线上,可设出切点,写出切线方程,结合已知条件求出切点坐标,从而得方程. 【高清课堂:导数的应用(理)394572知识要点】考点二、判定函数的单调性(1)函数的单调性与其导数的关系设函数y=f(x)在某个区间内可导,则当'()0f x >时,y=f(x)在相应区间上为增函数;当'()0f x <时,y=f(x) 在相应区间上为减函数;当恒有'()0f x =时,y=f(x)在相应区间上为常数函数。
要点诠释:①在区间(a,b)内,'()0f x >是f(x)在(a ,b)内单调递增的充分不必要条件!例如:32()'()30'(0)0,'()0(0)f x x f x x f f x x =⇒=≥=>≠,,而f(x)在R 上递增。
②学生易误认为只要有点使'()0f x =,则f(x)在(a ,b)上是常函数,要指出个别导数为零不影响函数的单调性,同时要强调只有在这个区间内恒有'()0f x =,这个函数y=f(x)在这个区间上才为常数函数。
【巩固练习】1.若()sin cos f x x α=-,则'()f α等于( ) A .sin α B .cos α C .sin cos αα+D .2sin α2.若函数2()f x x bx c =++的图象的顶点在第四象限,则函数'()f x 的图象是( )3.已知函数1)(23--+-=x ax x x f 在),(+∞-∞上是单调函数,则实数a 的取值范围是( )A .),3[]3,(+∞--∞B .]3,3[-C .),3()3,(+∞--∞D .)3,3(-4.对于R 上可导的任意函数()f x ,若满足'(1)()0x f x -≥,则必有( )A . (0)(2)2(1)f f f +< B. (0)(2)2(1)f f f +≤ C.(0)(2)2(1)f f f +≥ D. (0)(2)2(1)f f f +>5.若曲线4y x =的一条切线l 与直线480x y +-=垂直,则l 的方程为( )A .430x y --=B .450x y +-=C .430x y -+=D .430x y ++=6.函数)(x f 的定义域为开区间),(b a ,导函数)(x f '在),(b a 内的图象如图所示,则函数)(x f 在开区间),(b a 内有极小值点( )A .1个B .2个C .3个D .4个7.若函数()()2f x x x c =-在2x =处有极大值,则常数c 的值为_________; 8.函数x x y sin 2+=的单调增区间为 。
9.设函数())(0)f x ϕϕπ=+<<,若()()f x f x '+为奇函数,则ϕ=__________ 10.设321()252f x x x x =--+,当]2,1[-∈x 时,()f x m <恒成立,则实数m 的取值范围为 。
11.对正整数n ,设曲线)1(x x y n -=在2x =处的切线与y 轴交点的纵坐标为n a ,则数列1n a n ⎧⎫⎨⎬+⎩⎭的前n 项和的公式是12.设13()ln 1,22f x a x x x =+++其中a R ∈,曲线()y f x =在点(1,(1))f 处的切线垂直于y 轴. (Ⅰ) 求a 的值;(Ⅱ) 求函数()f x 的极值. 13.设1()(0)x x f x ae b a ae=++> (I)求()f x 在[0,)+∞上的最小值;(II)设曲线()y f x =在点(2,(2))f 的切线方程为32y x =;求,a b 的值. 14.已知函数32()f x x ax bx c =+++在23x =-与1x =时都取得极值 (1)求,a b 的值与函数()f x 的单调区间(2)若对[1,2]x ∈-,不等式2()f x c <恒成立,求c 的取值范围。
15.已知23()log x ax bf x x++=,(0,)x ∈+∞,是否存在实数a b 、,使)(x f 同时满足下列两个条件:(1))(x f 在(0,1)上是减函数,在[)1,+∞上是增函数;(2))(x f 的最小值是1,若存在,求出a b 、,若不存在,说明理由.16.已知函数()f x 满足满足121()(1)(0)2x f x f ef x x -'=-+;(1)求()f x 的解析式及单调区间; (2)若21()2f x x ax b ≥++,求(1)a b +的最大值. 【参考答案与解析】1.A【解析】''()sin ,()sin f x x f αα== 2.A 【解析】对称轴'0,0,()22bb f x x b -><=+,直线过第一、三、四象限 3.B【解析】'2()3210f x x ax =-+-≤在),(+∞-∞恒成立,24120a a ∆=-≤⇒≤≤4.C【解析】当1x ≥时,'()0f x ≥,函数()f x 在(1,)+∞上是增函数;当1x <时,'()0f x ≤,()f x 在(,1)-∞上是减函数,故()f x 当1x =时取得最小值,即有(0)(1),(2)(1),f f f f ≥≥得(0)(2)2(1)f f f +≥5.A【解析】与直线480x y +-=垂直的直线l 为40x y m -+=,即4y x =在某一点的导数为4,而34y x '=,所以4y x =在(1,1)处导数为4,此点的切线为430x y --=6.A【解析】极小值点应有先减后增的特点,即'''()0()0()0f x f x f x <→=→> 7.6【解析】'22'2()34,(2)8120,2,6f x x cx c f c c c =-+=-+==或,2c =时取极小值 8.(,)-∞+∞【解析】'2cos 0y x =+>对于任何实数都成立 9.6π【解析】''()))f x ϕϕϕ=-++=+()())3f x f x πϕ'+=++要使()()f x f x '+为奇函数,需且仅需,32k k Z ππϕπ+=+∈,即:,6k k Z πϕπ=+∈。
又0ϕπ<<,所以k 只能取0,从而6πϕ=。
10.(7,)+∞【解析】]2,1[-∈x 时,max ()7f x = 11.122n +- 【解析】 ()()/11222,:222(2)n n n x yn y n x --==-++=-+-切线方程为,令0x =,求出切线与y 轴交点的纵坐标为()012ny n =+,所以21n n a n =+,则数列1n a n ⎧⎫⎨⎬+⎩⎭的前n 项和()12122212n n n S +-==--12. 【解析】(1)因()13ln 122f x a x x x =+++,故()21322a f x x x '=-+ 由于曲线()y f x =在点()()1,1f 处的切线垂直于y 轴,故该切线斜率为0,即()10f '=,从而13022a -+=,解得1a =- (2)由(1)知()()13ln 1022f x x x x x =-+++>,()222113321222x x f x x x x--'=--+= ()2(31)(1)2x x f x x+-'∴=令()0f x '=,解得1211,3x x ==-(因213x =-不在定义域内,舍去), 当()0,1x ∈时,()0f x '<,故()f x 在()0,1上为减函数; 当()1,x ∈+∞时,()0f x '>,故()f x 在()1,+∞上为增函数; 故()f x 在1x =处取得极小值()13f =.13.【解析】(I)设(1)xt e t =≥;则2222111a t y atb y a at at at -'=++⇒=-=①当1a ≥时,0y '>⇒1y at b at=++在1t ≥上是增函数 得:当1(0)t x ==时,()f x 的最小值为1a b a++②当01a <<时,12y at b b at =++≥+当且仅当11(,ln )xat t e x a a ====-时,()f x 的最小值为2b +(II)11()()x xx x f x ae b f x ae ae ae'=++⇒=-由题意得:2222212(2)333131(2)222f ae b a ae e f ae b ae ⎧⎧=++==⎧⎪⎪⎪⎪⎪⇔⇔⎨⎨⎨'=⎪⎪⎪-==⎩⎪⎪⎩⎩14.【解析】(1)32'2(),()32f x x ax bx c f x x ax b =+++=++由'2124()0393f a b -=-+=,'(1)320f a b =++=得1,22a b =-=-'2f ,函数的单调区间如下表: 所以函数()f x 的递增区间是(,)3-∞-与(1,)+∞,递减区间是2(,1)3-;(2)321()2,[1,2]2f x x x x c x =--+∈-,当23x =-时,222()327f c -=+为极大值,而(2)2f c =+,则(2)2f c =+为最大值,要使2(),[1,2]f x c x <∈- 恒成立,则只需要2(2)2c f c >=+,得1,2c c <->或。
15.【解析】设2()x ax bg x x++=∵()f x 在(0,1)上是减函数,在[1,)+∞上是增函数 ∴()g x 在(0,1)上是减函数,在[1,)+∞上是增函数.∴⎩⎨⎧==3)1(0)1('g g ∴⎩⎨⎧=++=-3101b a b 解得⎩⎨⎧==11b a经检验,1,1a b ==时,()f x 满足题设的两个条件. 16. 【解析】(1)1211()(1)(0)()(1)(0)2x x f x f e f x x f x f e f x --'''=-+⇒=-+ 令1x =得:(0)1f =1211()(1)(0)(1)1(1)2x f x f e x x f f e f e --'''=-+⇒==⇔=得:21()()()12x xf x e x xg x f x e x '=-+⇒==-+()10()x g x e y g x '=+>⇒=在x R ∈上单调递增()0(0)0()0(0)0f x f x f x f x ''>=⇔>''<=⇔<得:()f x 的解析式为21()2xf x e x x =-+且单调递增区间为(0,)+∞,单调递减区间为(,0)-∞ (2)21()()(1)02x f x x ax b h x e a x b ≥++⇔=-+-≥ 得()(1)xh x e a '=-+ ①当10a +≤时,()0()h x y h x '>⇒=在x R ∈上单调递增x →-∞时,()h x →-∞与()0h x ≥矛盾②当10a +>时,()0ln(1),()0ln(1)h x x a h x x a ''>⇔>+<⇔<+得:当ln(1)x a =+时,min ()(1)(1)ln(1)0h x a a a b =+-++-≥22(1)(1)(1)ln(1)(10)a b a a a a +≤+-+++>令22()ln (0)F x x x x x =->;则()(12ln )F x x x '=-()00()0F x x F x x ''>⇔<<<⇔>当x =,max ()2e F x =当1,a b ==,(1)a b +的最大值为2e .。