信号与系统期末考试试题(有答案的)

期末试题一、选择题(每小题可能有一个或几个正确答案，将正确的题号填入［ ]内） 1．f （5-2t )是如下运算的结果-———-——-（ ） （A ）f (-2t ）右移5 （B)f （-2t ）左移5 （C ）f (-2t ）右移25 （D)f （—2t ）左移252．已知)()(),()(21t u e t f t u t f at -==，可以求得=)(*)(21t f t f —————(） （A ）1—at e - (B ）at e -(C ）)1(1at e a -- （D ）at e a-13．线性系统响应满足以下规律——-———-——-——( )（A)若起始状态为零,则零输入响应为零. （B ）若起始状态为零，则零状态响应为零。

（C ）若系统的零状态响应为零，则强迫响应也为零。

（D ）若激励信号为零，零输入响应就是自由响应。

4．若对f （t ）进行理想取样,其奈奎斯特取样频率为f s ,则对)231(-t f 进行取样，其奈奎斯特取样频率为—-—-———-( ）（A ）3f s (B ）s f 31 （C)3（f s —2） （D ）)2(31-s f 5．理想不失真传输系统的传输函数H （jω）是 —————-——（ ）（A ）0j t Ke ω- （B ）0t j Ke ω- (C)0t j Ke ω-[]()()c c u u ωωωω+--（D ）00j t Keω- （00,,,c t k ωω为常数)6．已知Z 变换Z 1311)]([--=z n x ,收敛域3z >,则逆变换x （n )为——（ ）（A ）)(3n u n （C)3(1)nu n -（B))(3n u n -- （D ）)1(3----n u n二．（15分）已知f(t ）和h （t)波形如下图所示，请计算卷积f(t)＊h （t)，并画出f(t)*h （t)波形。

三、（15分）四．（20分)已知连续时间系统函数H （s),请画出三种系统模拟框图(直接型/级联型/并联型）。

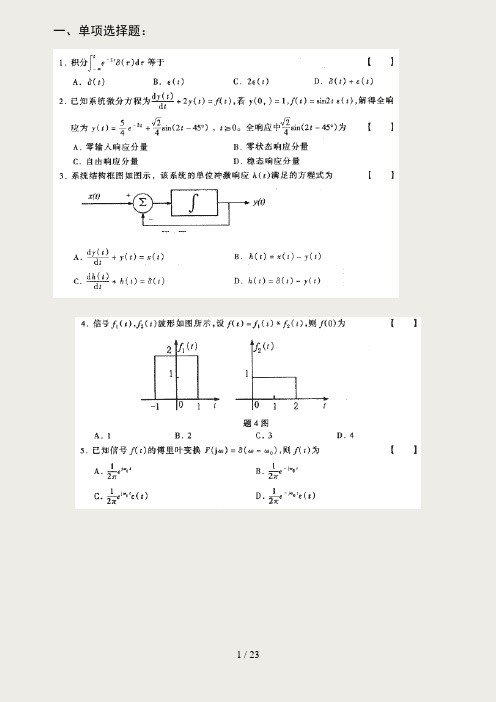
一、单项选择题：14、已知连续时间信号,)2(100)2(50sin )(--=t t t f 则信号t t f 410cos ·)(所占有的频带宽度为（） A ．400rad ／s B 。

200 rad ／s C 。

100 rad ／s D 。

50 rad ／s15、已知信号)(t f 如下图（a ）所示，其反转右移的信号f 1(t) 是（ ）16、已知信号)(1t f 如下图所示，其表达式是（ ）A 、ε（t ）＋2ε(t －2)－ε(t －3)B 、ε(t －1)＋ε(t －2)－2ε(t －3)C 、ε(t)＋ε(t －2)－ε(t －3)D 、ε(t －1)＋ε(t －2)－ε(t －3)17、如图所示：f （t ）为原始信号，f 1(t)为变换信号，则f 1(t)的表达式是（ ）A 、f(－t+1)B 、f(t+1)C 、f(－2t+1)D 、f(－t/2+1)18、若系统的冲激响应为h(t),输入信号为f(t),系统的零状态响应是（ ）19。

信号)2(4sin 3)2(4cos 2)(++-=t t t f ππ与冲激函数)2(-t δ之积为（ ）A 、2B 、2)2(-t δC 、3)2(-t δD 、5)2(-t δ，则该系统是（）＞－系统的系统函数．已知2]Re[,651)(LTI 202s s s s s H +++= A 、因果不稳定系统 B 、非因果稳定系统C 、因果稳定系统D 、非因果不稳定系统21、线性时不变系统的冲激响应曲线如图所示，该系统微分方程的特征根是（ ）A 、常数B 、 实数C 、复数D 、实数+复数22、线性时不变系统零状态响应曲线如图所示，则系统的输入应当是（ ）A 、阶跃信号B 、正弦信号C 、冲激信号D 、斜升信号23. 积分⎰∞∞-dt t t f )()(δ的结果为( )A )0(fB )(t f C.)()(t t f δ D.)()0(t f δ24. 卷积)()()(t t f t δδ**的结果为( ) A.)(t δ B.)2(t δ C. )(t f D.)2(t f25. 零输入响应是( )A.全部自由响应B.部分自由响应C.部分零状态响应D.全响应与强迫响应之差2A 、1-eB 、3eC 、3-e D 、127.信号〔ε(t)－ε(t －2)〕的拉氏变换的收敛域为 ( )A.Re[s]>0B.Re[s]>2C.全S 平面D.不存在28．已知连续系统二阶微分方程的零输入响应)(t y zi 的形式为t t Be Ae2--+，则其2个特征根为( ) A 。

信号与系统考试题及答案（一）1． 系统的激励是)t (e ，响应为)t (r ，若满足dt)t (de )t (r =，则该系统为 线性、时不变、因果。

（是否线性、时不变、因果？） 2． 求积分dt )t ()t (212-+⎰∞∞-δ的值为 5 。

3． 当信号是脉冲信号f(t)时，其 低频分量 主要影响脉冲的顶部，其 高频分量 主要影响脉冲的跳变沿。

4． 若信号f(t)的最高频率是2kHz ，则t)f(2的乃奎斯特抽样频率为 8kHz 。

5． 信号在通过线性系统不产生失真，必须在信号的全部频带内，要求系统幅频特性为 一常数相频特性为_一过原点的直线（群时延）。

6． 系统阶跃响应的上升时间和系统的 截止频率 成反比。

7． 若信号的3s F(s)=(s+4)(s+2)，求该信号的=)j (F ωj 3(j +4)(j +2)ωωω。

8． 为使LTI 连续系统是稳定的，其系统函数)s (H 的极点必须在S 平面的 左半平面 。

9． 已知信号的频谱函数是））00(()j (F ωωδωωδω--+=，则其时间信号f(t)为01sin()t j ωπ。

10． 若信号f(t)的211)s (s )s (F +-=，则其初始值=+)(f 0 1 。

二、判断下列说法的正误，正确请在括号里打“√”，错误请打“×”。

（每小题2分，共10分）1.单位冲激函数总是满足)()(t t -=δδ （ √ ）2.满足绝对可积条件∞<⎰∞∞-dt t f )(的信号一定存在傅立叶变换，不满足这一条件的信号一定不存在傅立叶变换。

（ × ） 3.非周期信号的脉冲宽度越小，其频带宽度越宽。

（ √ ）4.连续LTI 系统的冲激响应的形式取决于系统的特征根，于系统的零点无关。

（ √ ）5.所有周期信号的频谱都是离散谱，并且随频率的增高，幅度谱总是渐小的。

（ × ）三、计算分析题（1、3、4、5题每题10分，2题5分， 6题15分，共60分）1.信号)t (u e )t (f t-=21，信号⎩⎨⎧<<=其他，01012t )t (f ，试求)t (f *)t (f 21。

信号与系统期末考试题库及答案信号与系统期末考试题库及答案信号与系统期末考试题库及答案1.下列信号的分类⽅法不正确的是（ A ）：A 、数字信号和离散信号B 、确定信号和随机信号C 、周期信号和⾮周期信号D 、因果信号与反因果信号2.下列说法正确的是（ D ）：A 、两个周期信号x (t )，y (t )的和x (t )+y(t )⼀定是周期信号。

B 、两个周期信号x (t )，y (t )的周期分别为2和2，则其和信号x (t )+y(t ) 是周期信号。

C 、两个周期信号x (t )，y (t )的周期分别为2和π，其和信号x (t )+y(t )是周期信号。

D 、两个周期信号x (t )，y (t )的周期分别为2和3，其和信号x (t )+y(t )是周期信号。

3.下列说法不正确的是（ D ）。

A 、⼀般周期信号为功率信号。

B 、时限信号(仅在有限时间区间不为零的⾮周期信号)为能量信号。

C 、ε(t )是功率信号；D 、e t 为能量信号;4.将信号f (t )变换为（ A ）称为对信号f (t )的平移或移位。

A 、f (t –t 0)B 、f (ｋ–k 0)C 、f (at )D 、f (-t )5.将信号f (t )变换为（ A ）称为对信号f (t )的尺度变换。

A 、f (at )B 、f (t –k 0)C 、f (t –t 0)D 、f (-t )6.下列关于冲激函数性质的表达式不正确的是（ B ）。

A 、)()0()()(t f t t f δδ=B 、()t aat δδ1)(=C 、)(d )(t t- D 、)()-(t t δδ=7.下列关于冲激函数性质的表达式不正确的是（ D ）。

A 、?∞∞-='0d )(t t δ B 、)0(d )()(f t t t f =?+∞∞-δC 、)(d )(t tεττδ=?∞- D 、?∞∞-=')(d )(t t t δδ8.下列关于冲激函数性质的表达式不正确的是（ B ）。

信号与系统期末考试题及答案（第五套）符号说明：为符号函数，为单位冲击信号，为单位脉冲序列，为单位阶跃信号，为单位阶跃序列。

一、填空（共30分，每小题3分）1.。

2. 已知实信号的傅立叶变换，信号的傅立叶变换为。

3. 已知某连续时间系统的系统函数为，该系统属于类型。

低通4. 如下图A-1所示周期信号，其直流分量=。

4图A-15. 序列和=。

由于。

6. LTI 离散系统稳定的充要条件是。

的全部极点在单位圆内。

7. 已知信号的最高频率，对信号取样时，其频率不混迭的最大取样间隔=。

为。

8. 已知一连续系统在输入作用下的零状态响应，则该系统为系统（线性时变性）。

线性时变9. 若最高角频率为，则对取样，其频谱不混迭的最大间隔是。

)sgn(t )(t δ)(k δ)(t ε)(k ε________)42()3(55=+--⎰-dt t t δ5.0)3(21)2()3(21)42()3(25555-=-=---=+--=--⎰⎰t t dt t t dt t t δδ)(t f )()()(ωωωjX R j F +=)]()([21)(t f t f t y -+=)(ωj Y _________11)(+=s s H _________)(t f_________∑-∞=kn n )(ε_________)()1(0,00,1][k k k k k n kn εε+=⎩⎨⎧<≥+=∑-∞=_________)(z H )(t f )(0Hz f )2/(t f m ax T _________m axT 0max max 121f f T ==)(t f )4()(t f t y =_________)(t f m ω)2()4()(tf t f t y =_________mT ωπωπ34max max ==10. 已知的z 变换，得收敛域为时，是因果序列。

二、计算题（共50分，每小题10分）1. 某线性时不变连续时间系统的单位冲激响应和输入如图A-2所示，从时域求解该系统的零状态响应。

信号与系统期末考试题及答案（第⼀套）信号与系统期末考试题及答案（第⼀套）符号说明：为符号函数，为单位冲击信号，为单位脉冲序列，为单位阶跃信号，为单位阶跃序列。

⼀、填空（共30分，每⼩题3分）1. 已知某系统的输⼊输出关系为（其中X(0)为系统初始状态，为外部激励），试判断该系统是（线性、⾮线性）（时变、⾮时变）系统。

线性时变2. 。

03.4. 计算=。

5. 若信号通过某线性时不变系统的零状态响应为则该系统的频率特性=，单位冲激响应。

系统的频率特性，单位冲激响应。

6. 若的最⾼⾓频率为，则对信号进⾏时域取样，其频谱不混迭的最⼤取样间隔。

为7. 已知信号的拉式变换为，求该信号的傅⽴叶变换=。

不存在8. 已知⼀离散时间系统的系统函数，判断该系统是否稳定。

不稳定9.。

310. 已知⼀信号频谱可写为是⼀实偶函数，试问有何种对称性)sgn(t )(t δ)(k δ)(t ε)(k ε)0(2)()()(2X dt t df t f t t y +=)(t f ________________?∞-=-+32_________)221()32(dt t t t δ?∞∞-=--_________)24()22(dt t t εε??∞∞-==--1)24()22(21dt dt t t εε},3,5,2{)()},3()({2)(021=↓=--=K k f k k k f kεε)()(21k f k f *________}12,26,21,9,2{)()(21↓=*k f k f )(t f ),(),()(00为常数t K t t Kf t y f -=)(ωj H ________=)(t h ________0)(t j Ke j H ωω-=)()(0t t K t h -=δ)(t f )(Hz f m )2()()(t f t f t y ==max T ________m ax T )(6121max max s f f T m==)1)(1(1)(2-+=s s s F )(ωj F ______2121)(---+=z z z H ______=+-+?∞∞-dt t t t )1()2(2δ______)(,)()(3ωωωωA e A j F j -=)(t f。

一、单项选择题：14、已知连续时间信号,)2(100)2(50sin )(--=t t t f 则信号t t f 410cos ·)(所占有的频带宽度为（） A ．400rad ／s B 。

200 rad ／s C 。

100 rad ／s D 。

50 rad ／s15、已知信号)(t f 如下图（a ）所示，其反转右移的信号f 1(t) 是（ ）16、已知信号)(1t f 如下图所示，其表达式是（ ）A 、ε（t ）＋2ε(t －2)－ε(t －3)B 、ε(t －1)＋ε(t －2)－2ε(t －3)C 、ε(t)＋ε(t －2)－ε(t －3)D 、ε(t －1)＋ε(t －2)－ε(t －3)17、如图所示：f （t ）为原始信号，f 1(t)为变换信号，则f 1(t)的表达式是（ ）A 、f(－t+1)B 、f(t+1)C 、f(－2t+1)D 、f(－t/2+1)18、若系统的冲激响应为h(t),输入信号为f(t),系统的零状态响应是（ ）19。

信号)2(4sin 3)2(4cos 2)(++-=t t t f ππ与冲激函数)2(-t δ之积为（ ）A 、2B 、2)2(-t δC 、3)2(-t δD 、5)2(-t δ，则该系统是（）＞－系统的系统函数．已知2]Re[,651)(LTI 202s s s s s H +++= A 、因果不稳定系统 B 、非因果稳定系统C 、因果稳定系统D 、非因果不稳定系统21、线性时不变系统的冲激响应曲线如图所示，该系统微分方程的特征根是（ ）A 、常数B 、 实数C 、复数D 、实数+复数22、线性时不变系统零状态响应曲线如图所示，则系统的输入应当是（ ）A 、阶跃信号B 、正弦信号C 、冲激信号D 、斜升信号23. 积分⎰∞∞-dt t t f )()(δ的结果为( )A )0(fB )(t f C.)()(t t f δ D.)()0(t f δ24. 卷积)()()(t t f t δδ**的结果为( )A.)(t δB.)2(t δC. )(t fD.)2(t f25. 零输入响应是( )A.全部自由响应B.部分自由响应C.部分零状态响应D.全响应与强迫响应之差2A 、1-eB 、3eC 、3-eD 、127.信号〔ε(t)－ε(t －2)〕的拉氏变换的收敛域为 ( )A.Re[s]>0B.Re[s]>2C.全S 平面D.不存在28．已知连续系统二阶微分方程的零输入响应)(t y zi 的形式为tt Be Ae 2--+，则其2个特征根为() A 。

（完整版）《信号与系统》期末试卷与答案第 1 页共 6 页《信号与系统》期末试卷A 卷班级：学号：__________ 姓名：________ _ 成绩：_____________⼀．选择题（共10题，20分） 1、n j n j een x )34()32(][ππ+=，该序列是 D 。

A.⾮周期序列B.周期3=NC.周期8/3=ND. 周期24=N2、⼀连续时间系统y(t)= x(sint)，该系统是 C 。

A.因果时不变B.因果时变C.⾮因果时不变D. ⾮因果时变3、⼀连续时间LTI 系统的单位冲激响应)2()(4-=-t u et h t，该系统是 A 。

A.因果稳定B.因果不稳定C.⾮因果稳定D. ⾮因果不稳定4、若周期信号x[n]是实信号和奇信号，则其傅⽴叶级数系数a k 是 D 。

A.实且偶B.实且为奇C.纯虚且偶D. 纯虚且奇5、⼀信号x(t)的傅⽴叶变换⎩⎨⎧><=2||02||1)(ωωω，，j X ，则x(t)为 B 。

A.tt22sin B.t t π2sin C. t t 44sin D. ttπ4sin 6、⼀周期信号∑∞-∞=-=n n t t x )5()(δ，其傅⽴叶变换)(ωj X 为 A 。

A.∑∞-∞=-k k )52(52πωδπB. ∑∞-∞=-k k)52(25πωδπ C. ∑∞-∞=-k k )10(10πωδπD.∑∞-∞=-k k)10(101πωδπ7、⼀实信号x[n]的傅⽴叶变换为)(ωj e X ，则x[n]奇部的傅⽴叶变换为上⼀页下⼀页。

信号与系统期末考试题库及答案1.下列信号的分类方法不正确的是（ A ）：A 、数字信号和离散信号B 、确定信号和随机信号C 、周期信号和非周期信号D 、因果信号与反因果信号2.下列说法正确的是（ D ）：A 、两个周期信号x (t )，y (t )的和x (t )+y(t )一定是周期信号。

B 、两个周期信号x (t )，y (t )的周期分别为2和2，则其和信号x (t )+y(t ) 是周期信号。

C 、两个周期信号x (t )，y (t )的周期分别为2和π，其和信号x (t )+y(t )是周期信号。

D 、两个周期信号x (t )，y (t )的周期分别为2和3，其和信号x (t )+y(t )是周期信号。

3.下列说法不正确的是（ D ）。

A 、一般周期信号为功率信号。

B 、 时限信号(仅在有限时间区间不为零的非周期信号)为能量信号。

C 、ε(t )是功率信号；D 、e t 为能量信号;4.将信号f (t )变换为（ A ）称为对信号f (t )的平移或移位。

A 、f (t –t 0) B 、f (ｋ–k 0) C 、f (at ) D 、f (-t )5.将信号f (t )变换为（ A ）称为对信号f (t )的尺度变换。

A 、f (at ) B 、f (t –k 0) C 、f (t –t 0) D 、f (-t )6.下列关于冲激函数性质的表达式不正确的是（ B ）。

A 、)()0()()(t f t t f δδ=B 、()t aat δδ1)(=C 、)(d )(t tεττδ=⎰∞- D 、)()-(t t δδ=7.下列关于冲激函数性质的表达式不正确的是（ D ）。

A 、⎰∞∞-='0d )(t t δ B 、)0(d )()(f t t t f =⎰+∞∞-δC 、)(d )(t tεττδ=⎰∞- D 、⎰∞∞-=')(d )(t t t δδ8.下列关于冲激函数性质的表达式不正确的是（ B ）。

信号与系统期末考试试题一、选择题（共10题，每题3分 ，共30分，每题给出四个答案，其中只有一个正确的）1、 卷积f 1(k+5)*f 2(k-3) 等于 。

（A ）f 1(k)*f 2(k) （B ）f 1(k)*f 2(k-8)（C ）f 1(k)*f 2(k+8)（D ）f 1(k+3)*f 2(k-3)2、 积分dt t t ⎰∞∞--+)21()2(δ等于 。

（A ）1.25（B ）2.5（C ）3（D ）5 3、 序列f(k)=-u(-k)的z 变换等于 。

（A ）1-z z （B ）-1-z z（C ）11-z （D ）11--z4、 若y(t)=f(t)*h(t),则f(2t)*h(2t)等于 。

（A ）)2(41t y （B ）)2(21t y （C ）)4(41t y （D ）)4(21t y 5、 已知一个线性时不变系统的阶跃相应g(t)=2e -2t u(t)+)(t δ,当输入f(t)=3e —t u(t)时，系统的零状态响应y f (t)等于（A ）(-9e -t +12e -2t )u(t) （B ）(3-9e -t +12e -2t )u(t)（C ）)(t δ+(-6e -t +8e -2t )u(t) （D ）3)(t δ +(-9e -t +12e -2t )u(t)6、 连续周期信号的频谱具有（A ） 连续性、周期性 （B ）连续性、收敛性 （C ）离散性、周期性 （D ）离散性、收敛性7、 周期序列2)455.1(0+k COS π的 周期N 等于（A ） 1（B ）2（C ）3（D ）4 8、序列和()∑∞-∞=-k k 1δ等于（A ）1 (B) ∞ (C) ()1-k u (D) ()1-k ku9、单边拉普拉斯变换()se s s s F 2212-+=的愿函数等于 ()()t tu A ()()2-t tu B ()()()t u t C 2- ()()()22--t u t D 10、信号()()23-=-t u tet f t的单边拉氏变换()s F 等于()A ()()()232372+++-s e s s ()()223+-s e B s()()()2323++-s se C s ()()332++-s s e D s二、填空题（共9小题，每空3分，共30分）1、卷积和[（0.5）k+1u(k+1)]*)1(k -δ=________________________2、单边z 变换F(z)=12-z z的原序列f(k)=______________________ 3、已知函数f(t)的单边拉普拉斯变换F(s)=1+s s，则函数y(t)=3e -2t ·f(3t)的单边拉普拉斯变换Y(s)=_________________________4、频谱函数F(j ω)=2u(1-ω)的傅里叶逆变换f(t)=__________________5、单边拉普拉斯变换ss s s s F +++=2213)(的原函数f(t)=__________________________ 6、已知某离散系统的差分方程为)1(2)()2()1()(2-+=----k f k f k y k y k y ，则系统的单位序列响应h(k)=_______________________7、已知信号f(t)的单边拉氏变换是F(s),则信号⎰-=2)()(t dx x f t y 的单边拉氏变换Y(s)=______________________________8、描述某连续系统方程为()()()()()t f t f t y t y t y +=++''''52该系统的冲激响应h(t)=9、写出拉氏变换的结果()=t u 66 ，=k t 22三、（8分）四、（10分）如图所示信号()t f ，其傅里叶变换()()[]t f jw F F =，求（1） ()0F （2）()⎰∞∞-dw jw F六、（10分）某LTI 系统的系统函数()1222++=s s s s H ，已知初始状态()(),20,00=='=--y y 激励()(),t u t f =求该系统的完全响应。

信号与系统期末考试题库及答案1.以下信号的分类方法不正确的选项是〔 A 〕： A 、数字信号和离散信号 B 、确定信号和随机信号 C 、周期信号和非周期信号 D 、因果信号与反因果信号2.以下说法正确的选项是〔 D 〕：A 、两个周期信号x (t )，y (t )的和x (t )+y(t )一定是周期信号。

B 、两个周期信号x (t )，y (t )的周期分别为2和2，那么其和信号x (t )+y(t ) 是周期信号。

C 、两个周期信号x (t )，y (t )的周期分别为2和π，其和信号x (t )+y(t )是周期信号。

D 、两个周期信号x (t )，y (t )的周期分别为2和3，其和信号x (t )+y(t )是周期信号。

3.以下说法不正确的选项是〔 D 〕。

A 、一般周期信号为功率信号。

B 、 时限信号(仅在有限时间区间不为零的非周期信号)为能量信号。

C 、ε(t )是功率信号；D 、e t 为能量信号;f (t )变换为〔 A 〕称为对信号f (t )的平移或移位。

A 、f (t –t 0) B 、f (ｋ–k 0) C 、f (at ) D 、f (-t )f (t )变换为〔 A 〕称为对信号f (t )的尺度变换。

A 、f (at ) B 、f (t –k 0) C 、f (t –t 0) D 、f (-t )6.以下关于冲激函数性质的表达式不正确的选项是〔 B 〕。

A 、)()0()()(t f t t f δδ=B 、()t aat δδ1)(=C 、)(d )(t tεττδ=⎰∞- D 、)()-(t t δδ=7.以下关于冲激函数性质的表达式不正确的选项是〔 D 〕。

A 、⎰∞∞-='0d )(t t δ B 、)0(d )()(f t t t f =⎰+∞∞-δC 、)(d )(t tεττδ=⎰∞- D 、⎰∞∞-=')(d )(t t t δδ8.以下关于冲激函数性质的表达式不正确的选项是〔 B 〕。

信号与系统期末考试试卷（有详细答案）《信号与系统》考试试卷（时间120分钟）院/系专业姓名学号⼀、填空题（每⼩题2分，共20分）1．系统的激励是)t (e ，响应为)t (r ，若满⾜dt)t (de )t (r =，则该系统为线性、时不变、因果。

（是否线性、时不变、因果？）2．求积分dt )t ()t (212-+?∞∞-δ的值为 5 。

3．当信号是脉冲信号f(t)时，其低频分量主要影响脉冲的顶部，其⾼频分量主要影响脉冲的跳变沿。

4．若信号f(t)的最⾼频率是2kHz ，则t)f(2的乃奎斯特抽样频率为 8kHz 。

5．信号在通过线性系统不产⽣失真，必须在信号的全部频带内，要求系统幅频特性为⼀常数相频特性为_⼀过原点的直线（群时延）。

6．系统阶跃响应的上升时间和系统的截⽌频率成反⽐。

7．若信号的3s F(s)=(s+4)(s+2)，求该信号的=)j (F ωj 3(j +4)(j +2)ωωω。

8．为使LTI 连续系统是稳定的，其系统函数)s(H 的极点必须在S 平⾯的左半平⾯。

9．已知信号的频谱函数是））00(()j (F ωωδωωδω--+=，则其时间信号f(t)为01sin()t j ωπ。

10．若信号f(t)的211)s (s )s (F +-=，则其初始值=+)(f 0 1 。

⼆、判断下列说法的正误，正确请在括号⾥打“√”，错误请打“×”。

（每⼩题2分，共10分）1.单位冲激函数总是满⾜)()(t t -=δδ（ √ ）2.满⾜绝对可积条件∞不存在傅⽴叶变换。

（ × ） 3.⾮周期信号的脉冲宽度越⼩，其频带宽度越宽。

（ √ ）4.连续LTI 系统的冲激响应的形式取决于系统的特征根，于系统的零点⽆关。

（ √ ）5.所有周期信号的频谱都是离散谱，并且随频率的增⾼，幅度谱总是渐⼩的。

（ × ）三、计算分析题（1、3、4、5题每题10分，2题5分， 6题15分，共60分）1.信号)t (u e )t (f t -=21，信号<<=其他，01012t )t (f ，试求)t (f *)t (f 21。

格式《信号与系统》考试试卷（时间 120 分钟）院 / 系专业姓名学号题号一二三四五六七总分得分一、填空题（每小题 2 分，共 20 分）得分1．系统的激励是 e(t) ，响应为 r(t) ，若满足de(t)r ( t) ，则该系统为线性、时不变、因果。

dt（是否线性、时不变、因果？）2 的值为 5。

2．求积分 (t1)(t2)dt3．当信号是脉冲信号f(t)时，其低频分量主要影响脉冲的顶部，其高频分量主要影响脉冲的跳变沿。

4．若信号f(t)的最高频率是2kHz，则 f(2t)的乃奎斯特抽样频率为8kHz。

5．信号在通过线性系统不产生失真，必须在信号的全部频带内，要求系统幅频特性为一常数相频特性为 _一过原点的直线（群时延）。

6．系统阶跃响应的上升时间和系统的截止频率成反比。

．若信号的F(s)=3s j37。

，求该信号的 F ( j)(s+4)(s+2) (j+4)(j+2)8．为使LTI 连续系统是稳定的，其系统函数H(s ) 的极点必须在S 平面的左半平面。

1。

9．已知信号的频谱函数是0）(）F(( ，则其时间信号f(t)为0j)sin(t)js110．若信号 f(t)的F ( s ) ，则其初始值f(0)1。

2(s1 )得分二、判断下列说法的正误，正确请在括号里打“√”，错误请打“×”。

（每小题 2 分，共 10 分）《信号与系统》试卷第1页共 7页专业资料整理格式1.单位冲激函数总是满足 ( t )( t ) （√）2.满足绝对可积条件 f ( t ) dt 的信号一定存在傅立叶变换，不满足这一条件的信号一定不存在傅立叶变换。

（×）3.非周期信号的脉冲宽度越小，其频带宽度越宽。

（√）4.连续 LTI 系统的冲激响应的形式取决于系统的特征根，于系统的零点无关。

（√）5.所有周期信号的频谱都是离散谱，并且随频率的增高，幅度谱总是渐小的。

（×）得分三、计算分析题（1、 3、 4、 5 题每题 10 分， 2 题 5 分，6 题15 分，共 60 分）t 10t11.信号f(t)2eu(t) ，1，信号 f ，试求 f 1 (t)*f 2 (t)。

学号___________ 姓名_________ 贵州函授站得分______中国传媒大学远程与继续教育学院2010级广播电视技术专科第五学期《信号与系统》期末试卷一.单项选择题(本大题共10小题，每小题2分，共20分)。

1. 如右下图所示信号，其数学表示式为 (B)A. f (t ) = tu(t) − tu(t− 1)B. f (t ) = tu(t) − (t− 1)u (t− 1)C. f (t) = (1 − t )u (t) − (t− 1)u (t− 1)D. f (t ) = (1 + t )u (t) − (t + 1)u (t + 1)∞2. 序列和∑δ ( n ) 等于( A )n = − ∞C.u ( n)D. (n + 1)u ( n)A. 1B. ∞3. 已知：f (t ) = sgn(t ) 傅里叶变换为F ( jw) =2，则：F(jw)=jπsgn(w)的傅里叶jw1反变换f1(t)为(C)A. f1 (t ) =1B. f1 (t) = −2C. f1(t) = −1D. f1 (t ) =2t t t t24. 积分∫−2e tδ ( t− 3 ) dt等于(A)A. 0B. 1C. e3D. e−35. 周期性非正弦连续时间信号的频谱，其特点为 (C)A. 频谱是连续的，收敛的B. 频谱是离散的，谐波的，周期的C. 频谱是离散的，谐波的，收敛的D. 频谱是连续的，周期的6. 设： f (t ) ↔ F ( jw ) ，则： f 1 (t ) = f ( at − b ) ↔ F 1 ( jw ) 为( C ) A. F ( jw ) = aF ( j w ) ⋅ e − jbw B. F ( jw ) = 1 F ( j w ) ⋅ e − jbw1 a 1a aC. F ( jw ) = 1 F ( j w ) ⋅ e − j b wa 1 a a7. 已知某一线性时不变系统对信号H ( s ) = ( B )w − j b w D. F ( jw ) = aF ( j ) ⋅ e a1 a X (t ) 的零状态响应为 4 dX (t − 2) ，则该系统函数 dtA. 4 F ( s )B. 4 s⋅ e - 2SC. 4 e−2S / sD. 4 X ( s ) ⋅ e - 2S8. 单边拉普拉斯变换F ( s ) = 1 + s的原函数f (t ) = (D)A. e−t u (t )B. (1 + e−t )u (t )C. (t + 1)u (t )D. δ (t ) + δ' (t )9.如某一因果线性时不变系统的系统函数H(s)的所有极点的实部都小于零，则( C )A. 系统为非稳定系统B. | h(t) |<∞∞C. 系统为稳定系统D.∫0h (t )dt = 010. 离散线性时不变系统的单位序列响应h( n ) 为(A)A.输入为δ ( n ) 的零状态响应B.输入为u ( n ) 的响应C.系统的自由响应D.系统的强迫响应二.填空题(本大题共10小题，每小题2分，共20分)1. δ( −t ) =___ δ (t ) __ (用单位冲激函数表示 )。

《信号与系统》期末试卷A 卷班级： 学号：__________ 姓名：________ _ 成绩：_____________一． 选择题（共10题，20分） 1、n j n j een x )34()32(][ππ+=，该序列是 。

A.非周期序列B.周期3=NC.周期8/3=ND. 周期24=N2、一连续时间系统y(t)= x(sint)，该系统是 。

A.因果时不变B.因果时变C.非因果时不变D. 非因果时变3、一连续时间LTI 系统的单位冲激响应)2()(4-=-t u et h t，该系统是 。

A.因果稳定B.因果不稳定C.非因果稳定D. 非因果不稳定4、若周期信号x[n]是实信号和奇信号，则其傅立叶级数系数a k 是 。

A.实且偶B.实且为奇C.纯虚且偶D. 纯虚且奇5、一信号x(t)的傅立叶变换⎩⎨⎧><=2||02||1)(ωωω，，j X ，则x(t)为 。

A.tt22sin B.t t π2sin C. t t 44sin D. ttπ4sin 6、一周期信号∑∞-∞=-=n n t t x )5()(δ，其傅立叶变换)(ωj X 为 。

A.∑∞-∞=-k k )52(52πωδπB. ∑∞-∞=-k k)52(25πωδπ C. ∑∞-∞=-k k )10(10πωδπD.∑∞-∞=-k k)10(101πωδπ7、一实信号x[n]的傅立叶变换为)(ωj e X ，则x[n]奇部的傅立叶变换为 。

A. )}(Re{ωj eX j B. )}(Re{ωj e X C. )}(Im{ωj e X j D. )}(Im{ωj e X8、一信号x(t)的最高频率为500Hz ，则利用冲激串采样得到的采样信号x(nT)能唯一表示出原信号的最大采样周期为 。

A. 500 B. 1000 C. 0.05D. 0.0019、一信号x(t)的有理拉普拉斯共有两个极点s=－3和s=－5，若)()(4t x e t g t=，其傅立叶变换)(ωj G 收敛，则x(t)是 。

信号与系统》期末试卷 A 卷6、一周期信号x(t)(t n5n) ，其傅立叶变换 X(j) 为 A 2( 2k 5(2kA.) B.) 5k52k 51kC. 10(10 k)D.()k10 k107、一实信号 x[n]的傅立叶变换为 X(e j )，A. jRe{X(e j )}B. Re{X(e j )}C. jIm{ X(e j )}D.班级： 学号：姓名：成绩：1、 选择题(共 2j(3)nx[n] e 310题， 20 分)4j(3 )ne 3 ，该序列是2、 3、 4、 5、 A.非周期序列一连续时间系统 A. 因果时不变连续时间 A. 因果稳定若周期信号 A.实且偶LTI B. 周期 N 3C.周期 N 3/8y(t)= x(sint) ，该系统是B.因果时变C.非因果时不变D. 周期 N 24D. 非因果时变系统的单位冲激响应 4th(t) e 4tu(t 2) ，该系统是 AB.因果不稳定C.非因果稳定D. 非因果不稳定x[n] 是实信号和奇信号，则其傅立叶级数系数 B.实且为奇C.纯虚且偶a k 是DD. 纯虚且奇一信号 x(t)的傅立叶变换 X( j1，| | 0，| |222，则 x(t)为 sin2tA.2tB.sin2tsin4t C.4tsin4t D.t则 x[n] 奇 部 的 傅 立 叶 变 换 为Im{ X(e j )}8、一信号x(t) 的最高频率为500Hz，则利用冲激串采样得到的采样信号x(nT)能唯一表示出原信号的最大采样周期为 D 。

A. 500B. 1000C. 0.05D. 0.0019、一信号x(t) 的有理拉普拉斯共有两个极点s=－3 和s=－5，若g(t) e4t x(t) ，其傅立叶变换G( j ) 收敛，则x(t)是 C 。

A. 左边B. 右边C. 双边D. 不确定10、一系统函数H(s)se，Re{ s} 1 ，该系统是 C 。

s1A. 因果稳定B. 因果不稳定C. 非因果稳定D. 非因果不稳定二．简答题(共 6 题，40 分)1、 (10 分)下列系统是否是( 1)无记忆；(2)时不变；(3)线性；(4)因果；(5) 稳定，并说明理由。

一、单项选择题：14、已知连续时间信号,)2(100)2(50sin )(--=t t t f 则信号t t f 410cos ·)(所占有的频带宽度为（） A ．400rad ／s B 。

200 rad ／s C 。

100 rad ／s D 。

50 rad ／s15、已知信号)(t f 如下图（a ）所示，其反转右移的信号f 1(t) 是（ ）16、已知信号)(1t f 如下图所示，其表达式是（ ）A 、ε（t ）＋2ε(t －2)－ε(t －3)B 、ε(t －1)＋ε(t －2)－2ε(t －3)C 、ε(t)＋ε(t －2)－ε(t －3)D 、ε(t －1)＋ε(t －2)－ε(t －3)17、如图所示：f （t ）为原始信号，f 1(t)为变换信号，则f 1(t)的表达式是（ ）A 、f(－t+1)B 、f(t+1)C 、f(－2t+1)D 、f(－t/2+1)18、若系统的冲激响应为h(t),输入信号为f(t),系统的零状态响应是（ ）19。

信号)2(4sin 3)2(4cos 2)(++-=t t t f ππ与冲激函数)2(-t δ之积为（ ）A 、2B 、2)2(-t δC 、3)2(-t δD 、5)2(-t δ，则该系统是（）＞－系统的系统函数．已知2]Re[,651)(LTI 202s s s s s H +++= A 、因果不稳定系统 B 、非因果稳定系统C 、因果稳定系统D 、非因果不稳定系统21、线性时不变系统的冲激响应曲线如图所示，该系统微分方程的特征根是（ ）A 、常数B 、 实数C 、复数D 、实数+复数22、线性时不变系统零状态响应曲线如图所示，则系统的输入应当是（ ）A 、阶跃信号B 、正弦信号C 、冲激信号D 、斜升信号23. 积分⎰∞∞-dt t t f )()(δ的结果为( )A )0(fB )(t f C.)()(t t f δ D.)()0(t f δ24. 卷积)()()(t t f t δδ**的结果为( ) A.)(t δ B.)2(t δ C. )(t f D.)2(t f25. 零输入响应是( )A.全部自由响应B.部分自由响应C.部分零状态响应D.全响应与强迫响应之差2A 、1-eB 、3eC 、3-e D 、127.信号〔ε(t)－ε(t －2)〕的拉氏变换的收敛域为 ( )A.Re[s]>0B.Re[s]>2C.全S 平面D.不存在28．已知连续系统二阶微分方程的零输入响应)(t y zi 的形式为t t Be Ae2--+，则其2个特征根为( ) A 。

第1 页（共4 页）《信号与系统》须知：符号e (t)(t)、、e (k)(k)分别为单位阶跃函数和单位阶跃序列。

分别为单位阶跃函数和单位阶跃序列。

LTI 表示线性时不变。

为加法器。

一、单项选择题（每小题4分，共32分）D 1、序列和33(2)ii i d ¥-=-¥-å等于A ．3e (k –2)B ．3e (k)C ．1D ．3 D 2、积分55(1)d 2t t e t d --ò等于A ．0B ．1C ．eD ．e 2 B 3、()(a )f t t d =A ．(0)f t d()B ．1(0)()|a |f t d C ．(0)f aD ．0()f t a æöd ç÷èøB 4、1()f t 、2()f t 波形如题4图所示，12()()*()f t f t f t =则(2)f =t1()f t -22240t2()f t 11-120题4图A ．12B ．1C ．32D ．2 B 5、已知)()()(21k f k f k f *=，)(1k f 、)(2k f 波形如题5图所示，)0(f 等于1()f k 012312()f k 011-11kk题5图A ．1B ．2C ．3D ．4 D 6、已知()1sgn()f t t =+则其傅立叶变换的频谱函数()F j w 等于A ．12()j pd w +w B ．2j wC ．1()j pd w +wD ．2()j 2pd w +w∑D 7、已知单边拉普拉斯变换的象函数22()1F s s =+则原函数)(t f 等于等于A ．()te t -e B ．2()te t -e C ．2cos ()t t e D ．2sin ()t t e B 8、已知)()(k k kf e =，其双边Z 变换的象函数)(z F 等于等于 A ．1-z z B ．2)1(-z z C ．1--z z D ．2)1(--z z二、填空题（每小题5分，共30分）分） 9、单边拉普拉斯变换定义()F S =0()stf t e dt-¥-ò；双边Z 变换定义式()F Z =()kk f k z¥-=-¥å10、已知()f t 的波形如题10图所示，则(12)f t -波形波形 (1) ；()df t dt波形波形(2) 。