信号与系统期末试卷及参考答案

一．填空题（本大题共10空，每空2分，共20分。

) 1．()*(2)k k εδ-= (2)k ε- 。

2．sin()()2td πτδττ-∞+=⎰()u t 。

3. 已知信号的拉普拉斯变换为1s a-，若实数a a >0 或 大于零 ，则信号的傅里叶变换不存在.4. ()()()t h t f t y *=，则()=t y 2 ()()t h t f 222* .5. 根据Parseval 能量守恒定律,计算⎰∞∞-=dt t t 2)sin (π 。

注解： 由于)(sin 2ωπg t t⇔，根据Parseval 能量守恒定律，可得πωππωωππ===⎪⎭⎫⎝⎛⎰⎰⎰-∞∞-∞∞-d d g dt t t 11222221)(21sin6. 若)(t f 最高角频率为m ω，则对)2()4()(tf t f t y =取样，其频谱不混迭的最大间隔是 m T ωπωπ34max max ==注解：信号)(t f 的最高角频率为m ω，根据傅立叶变换的展缩特性可得信号)4/(t f 的最高角 频率为4/m ω,信号)2/(t f 的最高角频率为2/m ω。

根据傅立叶变换的乘积特性，两信号时域相乘，其频谱为该两信号频谱的卷积，故)2/()4/(t f t f 的最高角频率为m mmωωωω4324max =+=根据时域抽样定理可知，对信号)2/()4/(t f t f 取样时,其频谱不混迭的最大抽样间隔m axT 为mT ωπωπ34max max ==7. 某因果线性非时变（LTI ）系统，输入)()(t t f ε=时,输出为:)1()()(t t e t y t--+=-εε；则)2()1()(---=t t t f εε时，输出)(t y f ＝)1()2()()1()2()1(t t e t t e t t -----+-----εεεε。

8. 已知某因果连续LTI 系统)(s H 全部极点均位于s 左半平面,则∞→t t h )(的值为0 。

信号与系统考试题及答案（一）1． 系统的激励是)t (e ，响应为)t (r ，若满足dt)t (de )t (r =，则该系统为 线性、时不变、因果。

（是否线性、时不变、因果？） 2． 求积分dt )t ()t (212-+⎰∞∞-δ的值为 5 。

3． 当信号是脉冲信号f(t)时，其 低频分量 主要影响脉冲的顶部，其 高频分量 主要影响脉冲的跳变沿。

4． 若信号f(t)的最高频率是2kHz ，则t)f(2的乃奎斯特抽样频率为 8kHz 。

5． 信号在通过线性系统不产生失真，必须在信号的全部频带内，要求系统幅频特性为 一常数相频特性为_一过原点的直线（群时延）。

6． 系统阶跃响应的上升时间和系统的 截止频率 成反比。

7． 若信号的3s F(s)=(s+4)(s+2)，求该信号的=)j (F ωj 3(j +4)(j +2)ωωω。

8． 为使LTI 连续系统是稳定的，其系统函数)s (H 的极点必须在S 平面的 左半平面 。

9． 已知信号的频谱函数是））00(()j (F ωωδωωδω--+=，则其时间信号f(t)为01sin()t j ωπ。

10． 若信号f(t)的211)s (s )s (F +-=，则其初始值=+)(f 0 1 。

二、判断下列说法的正误，正确请在括号里打“√”，错误请打“×”。

（每小题2分，共10分）1.单位冲激函数总是满足)()(t t -=δδ （ √ ）2.满足绝对可积条件∞<⎰∞∞-dt t f )(的信号一定存在傅立叶变换，不满足这一条件的信号一定不存在傅立叶变换。

（ × ） 3.非周期信号的脉冲宽度越小，其频带宽度越宽。

（ √ ）4.连续LTI 系统的冲激响应的形式取决于系统的特征根，于系统的零点无关。

（ √ ）5.所有周期信号的频谱都是离散谱，并且随频率的增高，幅度谱总是渐小的。

（ × ）三、计算分析题（1、3、4、5题每题10分，2题5分， 6题15分，共60分）1.信号)t (u e )t (f t-=21，信号⎩⎨⎧<<=其他，01012t )t (f ，试求)t (f *)t (f 21。

信号与系统期末试题及答案（第一套）符号说明：为符号函数，为单位冲击信号，为单位脉冲序列，为单位阶跃信号，为单位阶跃序列。

一、填空（共30分，每小题3分）1. 矩形脉冲波形（高度为A,宽度为b ）的信号能量为_____________。

2. 序列的自相关是一个偶对称函数，它满足关系式_____________。

3. 线性时不变连续稳定的因果系统，其传输函数的极点位于_____全部位于左半开复平面 ______。

4. 某线性时不变系统的单位冲激响应若为，则系统是___五阶________系统。

（几阶系统）5. 的傅立叶反变换为_____________。

6. 已知周期信号的第三次谐波的幅度等于3，则信号的第三次谐波的幅度等于___3__________。

7. 令，，如果，试求其和__8______。

8. 卷积____________。

9. 信号，a>0的傅立叶变换为______；_____。

10. 已知，，则。

二、计算题（共50分，每小题10分）1．某理想低通滤波器，其频率响应为当基波周期为，其傅里叶级数系数为的信号输入到滤波器时，滤波器的输出为，且。

问对于什么样的值，才保证？1、解：信号的基波角频率为：。

信号通过理想低通滤波器后，输出是其本身，这意味着信号所有频率分量均在低通滤波器的通带内。

由于周期)sgn(t )(t δ)(k δ)(t ε)(k εb A E 2=()k x )(k r xx )0()(xx xx r k r ≤)(s H )()2cos()()(t t t t e t h tεε⋅⋅+=-9)5(3)(2++=ωωj j F )(t f )()3sin(5t t e tε⋅-)(t f )2(t f kk x 2)(=)3()(-=k k y δ)()()(k y k x k z ==∑)(k z =-)(*)(t e t t εε)()1(t e tε--ta en x -=)(222ω+a a111)(--=az z X a z >=)(k x )()(k a k x k ε=⎩⎨⎧>≤=100,0100,1)(ωωωj H 6π=T n a )(t f )(t y )()(t f t y =n 0=n a )(t f ==T πω2012s rad /)(t f )(t f信号含有丰富的高次谐波分量，只有当高次谐波分量的幅度非常小时，对的贡献才忽略不计。

一、单项选择题：14、已知连续时间信号,)2(100)2(50sin )(--=t t t f 则信号t t f 410cos ·)(所占有的频带宽度为（） A ．400rad ／s B 。

200 rad ／s C 。

100 rad ／s D 。

50 rad ／s15、已知信号)(t f 如下图（a ）所示，其反转右移的信号f 1(t) 是（ ）16、已知信号)(1t f 如下图所示，其表达式是（ ）A 、ε（t ）＋2ε(t －2)－ε(t －3)B 、ε(t －1)＋ε(t －2)－2ε(t －3)C 、ε(t)＋ε(t －2)－ε(t －3)D 、ε(t －1)＋ε(t －2)－ε(t －3)17、如图所示：f （t ）为原始信号，f 1(t)为变换信号，则f 1(t)的表达式是（ ）A 、f(－t+1)B 、f(t+1)C 、f(－2t+1)D 、f(－t/2+1)18、若系统的冲激响应为h(t),输入信号为f(t),系统的零状态响应是（ ）19。

信号)2(4sin 3)2(4cos 2)(++-=t t t f ππ与冲激函数)2(-t δ之积为（ ）A 、2B 、2)2(-t δC 、3)2(-t δD 、5)2(-t δ，则该系统是（）＞－系统的系统函数．已知2]Re[,651)(LTI 202s s s s s H +++= A 、因果不稳定系统 B 、非因果稳定系统C 、因果稳定系统D 、非因果不稳定系统21、线性时不变系统的冲激响应曲线如图所示，该系统微分方程的特征根是（ ）A 、常数B 、 实数C 、复数D 、实数+复数22、线性时不变系统零状态响应曲线如图所示，则系统的输入应当是（ ）A 、阶跃信号B 、正弦信号C 、冲激信号D 、斜升信号23. 积分⎰∞∞-dt t t f )()(δ的结果为( )A )0(fB )(t f C.)()(t t f δ D.)()0(t f δ24. 卷积)()()(t t f t δδ**的结果为( )A.)(t δB.)2(t δC. )(t fD.)2(t f25. 零输入响应是( )A.全部自由响应B.部分自由响应C.部分零状态响应D.全响应与强迫响应之差2A 、1-eB 、3eC 、3-eD 、127.信号〔ε(t)－ε(t －2)〕的拉氏变换的收敛域为 ( )A.Re[s]>0B.Re[s]>2C.全S 平面D.不存在28．已知连续系统二阶微分方程的零输入响应)(t y zi 的形式为tt Be Ae 2--+，则其2个特征根为() A 。

信号与系统》期末试卷与答案信号与系统》期末试卷A卷班级：__________ 学号：_________ 姓名：_________ 成绩：_________一．选择题（共10题，20分）1、序列x[n] = e^(j(2πn/3)) + e^(j(4πn/3))，该序列的周期是：A。

非周期序列B。

周期 N = 3C。

周期 N = 3/8D。

周期 N = 242、连续时间系统 y(t) = x(sin(t))，该系统是：A。

因果时不变B。

因果时变C。

非因果时不变D。

非因果时变3、连续时间LTI 系统的单位冲激响应h(t) = e^(-4t)u(t-2)，该系统是：A。

因果稳定B。

因果不稳定C。

非因果稳定D。

非因果不稳定4、若周期信号 x[n] 是实信号和奇信号，则其傅立叶级数系数 a_k 是：A。

实且偶B。

实且为奇C。

纯虚且偶D。

纯虚且奇5、信号x(t) 的傅立叶变换X(jω) = {1，|ω|2}，则x(t) 为：A。

sin(2t)/2tB。

sin(2t)sin(4t)sin(4t)/πtC。

0D。

16、周期信号x(t) = ∑δ(t-5n)，其傅立叶变换X(jω) 为：A。

∑δ(ω-5)B。

∑δ(ω-10πk)C。

5D。

10πjω7、实信号 x[n] 的傅立叶变换为X(e^jω)，则 x[n] 奇部的傅立叶变换为：A。

jRe{X(e^jω)}B。

Re{X(e^jω)}C。

jIm{X(e^jω)}D。

Im{X(e^jω)}8、信号 x(t) 的最高频率为 500Hz，则利用冲激串采样得到的采样信号 x(nT) 能唯一表示出原信号的最大采样周期为：A。

500B。

1000C。

0.05D。

0.0019、信号 x(t) 的有理拉普拉斯共有两个极点 s = -3 和 s = -5，若 g(t) = e^(xt)，其傅立叶变换G(jω) 收敛，则 x(t) 是：A。

左边B。

右边C。

双边D。

不确定10、系统函数 H(s) = (s+1)/s，Re(s)。

信号与系统期末考试试卷（有详细答案）《信号与系统》考试试卷（时间120分钟）院/系专业姓名学号⼀、填空题（每⼩题2分，共20分）1．系统的激励是)t (e ，响应为)t (r ，若满⾜dt)t (de )t (r =，则该系统为线性、时不变、因果。

（是否线性、时不变、因果？）2．求积分dt )t ()t (212-+?∞∞-δ的值为 5 。

3．当信号是脉冲信号f(t)时，其低频分量主要影响脉冲的顶部，其⾼频分量主要影响脉冲的跳变沿。

4．若信号f(t)的最⾼频率是2kHz ，则t)f(2的乃奎斯特抽样频率为 8kHz 。

5．信号在通过线性系统不产⽣失真，必须在信号的全部频带内，要求系统幅频特性为⼀常数相频特性为_⼀过原点的直线（群时延）。

6．系统阶跃响应的上升时间和系统的截⽌频率成反⽐。

7．若信号的3s F(s)=(s+4)(s+2)，求该信号的=)j (F ωj 3(j +4)(j +2)ωωω。

8．为使LTI 连续系统是稳定的，其系统函数)s(H 的极点必须在S 平⾯的左半平⾯。

9．已知信号的频谱函数是））00(()j (F ωωδωωδω--+=，则其时间信号f(t)为01sin()t j ωπ。

10．若信号f(t)的211)s (s )s (F +-=，则其初始值=+)(f 0 1 。

⼆、判断下列说法的正误，正确请在括号⾥打“√”，错误请打“×”。

（每⼩题2分，共10分）1.单位冲激函数总是满⾜)()(t t -=δδ（ √ ）2.满⾜绝对可积条件∞不存在傅⽴叶变换。

（ × ） 3.⾮周期信号的脉冲宽度越⼩，其频带宽度越宽。

（ √ ）4.连续LTI 系统的冲激响应的形式取决于系统的特征根，于系统的零点⽆关。

（ √ ）5.所有周期信号的频谱都是离散谱，并且随频率的增⾼，幅度谱总是渐⼩的。

（ × ）三、计算分析题（1、3、4、5题每题10分，2题5分， 6题15分，共60分）1.信号)t (u e )t (f t -=21，信号<<=其他，01012t )t (f ，试求)t (f *)t (f 21。

《信号与系统》期末试卷A 卷班级：班级： 学号：__________ 姓名：________ _ 成绩：_____________ 一． 选择题（共10题，20分） 1、nj nj een x )34()32(][p p +=，该序列是，该序列是 。

A.非周期序列 B.周期3=NC.周期8/3=ND. 周期24=N2、一连续时间系统y(t)= x(sint)，该系统是，该系统是 。

A.因果时不变 B.因果时变因果时变C.非因果时不变非因果时不变D. 非因果时变非因果时变3、一连续时间L TI 系统的单位冲激响应)2()(4-=-t u et h t，该系统是，该系统是 。

A.因果稳定因果稳定B.因果不稳定因果不稳定C.非因果稳定非因果稳定D. 非因果不稳定非因果不稳定4、若周期信号x[n]是实信号和奇信号，则其傅立叶级数系数a k 是 。

A.实且偶 B.实且为奇实且为奇C.纯虚且偶纯虚且偶D. 纯虚且奇纯虚且奇5、一信号x(t)的傅立叶变换îíì><=2||02||1)(w w w ，，j X ，则x(t)为 。

A. tt 22sin B. ttp 2sin C. tt 44sin D. ttp 4sin6、一周期信号å¥-¥=-=n n t t x )5()(d ，其傅立叶变换)(w j X 为。

A. å¥-¥=-k k )52(52p w d p B. å¥-¥=-k k )52(25p w d pC. å¥-¥=-k k )10(10p w d pD. å¥-¥=-k k)10(101p w d p7、一实信号x[n]的傅立叶变换为)(wj eX ，则x[n]奇部的傅立叶变换为奇部的傅立叶变换为 。

A. )}(Re{wj eX j B. )}(Re{wj eX C. )}(Im{wj eX j D. )}(Im{wj eX8、一信号x(t)的最高频率为500Hz ，则利用冲激串采样得到的采样信号x(nT)能唯一表示出原信号的最大采样周期为表示出原信号的最大采样周期为 。

《信号与系统》期末试卷A 卷班级： 学号：__________ 姓名：________ _ 成绩：_____________一． 选择题（共10题，20分） 1、n j n j een x )34()32(][ππ+=，该序列是 。

A.非周期序列B.周期3=NC.周期8/3=ND. 周期24=N2、一连续时间系统y(t)= x(sint)，该系统是 。

A.因果时不变B.因果时变C.非因果时不变D. 非因果时变3、一连续时间LTI 系统的单位冲激响应)2()(4-=-t u et h t，该系统是 。

A.因果稳定B.因果不稳定C.非因果稳定D. 非因果不稳定4、若周期信号x[n]是实信号和奇信号，则其傅立叶级数系数a k 是 。

A.实且偶B.实且为奇C.纯虚且偶D. 纯虚且奇5、一信号x(t)的傅立叶变换⎩⎨⎧><=2||02||1)(ωωω，，j X ，则x(t)为 。

A.tt22sin B.t t π2sin C. t t 44sin D. ttπ4sin 6、一周期信号∑∞-∞=-=n n t t x )5()(δ，其傅立叶变换)(ωj X 为 。

A.∑∞-∞=-k k )52(52πωδπB. ∑∞-∞=-k k)52(25πωδπ C. ∑∞-∞=-k k )10(10πωδπD.∑∞-∞=-k k)10(101πωδπ7、一实信号x[n]的傅立叶变换为)(ωj e X ，则x[n]奇部的傅立叶变换为 。

A. )}(Re{ωj eX j B. )}(Re{ωj e X C. )}(Im{ωj e X j D. )}(Im{ωj e X8、一信号x(t)的最高频率为500Hz ，则利用冲激串采样得到的采样信号x(nT)能唯一表示出原信号的最大采样周期为 。

A. 500 B. 1000 C. 0.05D. 0.0019、一信号x(t)的有理拉普拉斯共有两个极点s=－3和s=－5，若)()(4t x e t g t=，其傅立叶变换)(ωj G 收敛，则x(t)是 。

《信号与系统》须知：符号(t)、(k)分别为单位阶跃函数和单位阶跃序列。

LTI 表示线性时不变。

丄为加法器。

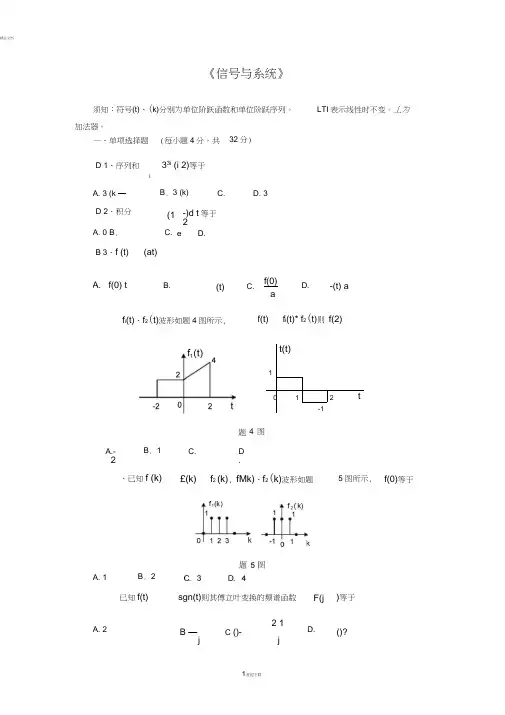
一、单项选择题 (每小题4分，共 32分) D 1、序列和 i 33i (i 2)等于 A. 3 (k — D 2、积分 A. 0 B . B . 3 (k) -)d t 等于2eD.C. D. 3 (1 C. B 3、f (t)(at)A. f(0) tB.(t)C.f(0) a D.-(t) af(t)f i (t)* f 2(t)则 f(2)A.-2A. 1 A. 2f i (t)、f 2(t)波形如题4图所示, 图4 C.B . 1D .t(t)112t-1、已知f (k)£(k)B . 2 已知f(t)f 2 (k), fMk)、f 2(k)波形如题sgn(t)则其傅立叶变换的频谱函数F(j5图所示,f(0)等于)等于2 1 B —C ()- jjD.()?D 7、已知单边拉普拉斯变换的象函数 F(S ) 22则原函数f(t)等于S 1A. e t (t)B . 2e t (t)C. 2cost (t)D. 2sin t (t)B 8、已知f(k) k (k)，其双边Z 变换的象函数F(z)等于kkf(k) ( 1)3 4 ,k 012、 f (t)2 t2te 则其单边拉普拉斯变换的象函数3F(s) 2花13、已知信号流图如题 13图所示，则系统函数 H(z)2z 2 z 12z 2 3z 3AzBzCzz 1(z1)2z 1二、填空题 (每小题5分，共 30分)D.z(z 1)2f (t)e st dt ;双边Z 变换定义式F(Z)f (k)z10、已知f(t)的波形如题10图所示，贝y f (1 2t)波形(1)F(z)(2)玉且其收敛域为 1 z 4，则其对应的原函数z 49、单边拉普拉斯变换定义F(S)f 波形⑵11、已知象函数题10图14、已知f(t)的傅立叶变换F(j )，则其原函数f (t) = 2e t (t) j 1 -----------三、计算题(38分)请你写出简明解题步骤；只有答案得 0分。

一、单项选择题:L 积分「卡7出〔 Cdf 等于 【】AB. €</〕C. 2e 〔0D.2 .系统做分方程为吗立+假设L/C 〕,由SeC 〕.解得全响d 〔应为小〕=上■"浮&⑵—符〕第4.口全响通中事i"2"45"〕为 [1M 零输入响应分量 凤零状态响应分量 c.自由响应分at口.程态响厘分量3 .系统结构框图如图示.诿系统的单位冲激响应h 〔.牖区的方程式为[ I4 .信号.力C 〕波形如下图.设小.之£.〕,人〔..那么f 〔D 〕为A.D,$FC)C.dvU)di + y<f} = x(；) fl. h(t) =<t(0 - y(t)口. h ⑴口,(0 - y(H$.信号/"〕的傅里叶变换卜仃时〕=双始C. 3口. 4-州,那么/■〕为口H. 26.信号/3〕如下图一那么其傅里叶变换为7 .信号f 3〕和工分别如图储〕和图〔b 〕所示,声1尤〔力]=匕〔讪〕,那么£口〕的傅里叶变换为FE)"心有一因果线性时不变系统,其频率响应那么讪〕=-3,对于某1输入日"所得输出信号的傅里叶变换为 修山> =尸一用一 哈,那么诚雅人 M 〕为[ ]〔ja -t 2 jw + 刃 A. +〞小〕 B. <3,e 〔r 〕C . — e 1* e 〔i 〕EL J9.必/屋1〕的拉氏变换及收敛域为【1A.白. R C 〔J ! > -2B.』, 版㈤ <-23 r M J5 T C.—^=〔 Rehl > 2I 〕. ReH| < 2 题6图0)题7图艮H.占一2 j - 20/〔.= .3 7〔—1〕的拉氏变班为I 】c . s(l - e -J > u, •一) H. F3) = -T-J RelM a -2的拉氏反变疑为 i +5i4-6A,[* ** +2f l,]e(r) B, (>"-2f 〞・ C. S(t) + c^'etr)D. e h HO12 .阳〔&〕中前段电路是某夏杂电路的一都分.其中里悬心和电容C 都含有初始欣态,请HUH (b)13 .寓融信号f"〕是指 t ]A M 的取值是连续的.而CG 的取值是任意的信号B.n 的取值是离散的,而人公的取值是任意的信号C.m 的敷便是连续的•而f"〕的取值是连续的信号D.rt 的顺值是注续的,而f 〔n 〕的取值是高散的信号14、连续时间信号f 〔t 〕 "n 50〔t 2〕,那么信号f 〔t 〕 COS104t 所占有的频带宽度为〔〕100〔t 2〕A. 400rad/s B .200 rad /s C .100 rad/s D .50 rad/s15、信号f 〔t 〕如以下图〔a 〕所示,其反转右移的信号 f 1〔t 〕是〔〕在图〔b 〕中选出该电路的发续域模型a题12图(«)0 12 3 4A 、£ (t) +2e (^2)- £ (^3) C 、s (tf £ (^2)- £ 什 3)B 、e 什 1)+ e / 2)—2e (t- 3) D 、£ (^1)+ £ (A2) — £ 也 3)B 、f(t+1) D 、f(-t/2+1)18、假设系统的冲激响应为 h(t),输入信号为f(t),系统的零状态响应是()f l (t)的表达式是(17、如下图：f (t)为原始信号,f i (t)为变换信号,那么 A 、f(—t+1) C 、f(-2t+1)16、信号f i (t)如以下图所示,其表达式是(19.信号f(t) 2cos—(t 2) 3sin-(t 2)与冲激函数(t 2)之积为()4 4A、2B、2 (t 2)C、3 (t 2)D、5 (t 2)20.LTI系统的系统函数H 〔s〕2S 1一,Re[s]>—2,那么该系统是〔〕s 5s 6A、因果不稳定系统B、非因果稳定系统C、因果稳定系统D、非因果不稳定系统21、线性时不变系统的冲激响应曲线如下图,该系统微分方程的特征根是〔〕22、线性时不变系统零状态响应曲线如下图,那么系统的输入应当是〔A、阶跃信号B、正弦信号C、冲激信号D、斜升信号23.积分f (t) (t)dt的结果为()A o — 1, 一229.函数.)是(A.奇函数B.一1, 2 )Bo偶函数Co 1, - 2Co非奇非偶函数( )Co 函数Do 1 , 2Do奇谐函数Do无法给出Do功率P=)Do带阻滤波器S,那么矩形脉冲的FT (傅氏变换)在原点处的函数值等于()A f(0)24 .卷积(t) f (t)A. (t)25 .零输入响应是( A.全部自由响应 C.局部零状态响应B f(t)⑴的结果为(B. (2t)C. f(t) (t))C. f(t)D. f(0) (t)D. f(2t)2 A、e 1)B.局部自由响应D.全响应与强迫响应之差c 3B、e D、127.信号〔e (t)- s什2)〕的拉氏变换的收敛域为()A.Re[s]>0B.Re[s]>2C.全S 平面D.不存在28.连续系统二阶微分方程的零输入响应y zi (t)的形式为Ae t Be 2t,那么其2个特征根为()30 .周期矩形脉冲序列的频谱的谱线包络线为A. 函数Bo Sa函数31 .能量信号其()A,能量E=0 Bo功率P=0 Co能量E =32 .在工程上,从抽样信号恢复原始信号时需要通过的滤波器是(A .高通滤波器B.低通滤波器Co带通滤波器33.设一个矩形脉冲的面积为A. S/2 Bo S/3 Co S/ 4 Do S34. f (k) sin 3k, k 0, 1, 2, 3, ••是(A.周期信号35.线性系统具有〔A.分解特性Bo非周期信号〕Bo零状态线性Co不能表示信号Co零输入线性Do以上都不对Do ABC36.设系统零状态响应与鼓励的关系y zs(t) f 〔t〕,那么以下表述不对的是〔A.系统是线性的Bo系统是时不变的Co系统是因果的Do系统是稳定的37.对于信号f〔t〕 sin 2 t的最小取样频率是A. 1 Hz38.理想低通滤波器是Bo 2)Hz Co 4 Hz Do 8 Hz39. A.因果系统Co非因果系统方具有〔BoDo物理可实现系统响应不超前于鼓励发生的系统A.微分特性Bo积分特性Co延时特性Do因果特性40. sin (t 2) (t 1〕等于A. sin (t 2) Bo (t 1) Co 1 Do 041.功率信号其〔A,能量E=0 Bo 功率P=0 Co能量E= D o功率P =42 .信号f (k) sin — k,k 6 0, 1, 2, 3, 其周期是〔A. 2B.12 Co D.不存在43.对于信号f〔t〕sin 2 310 t sin 4 310 t的最小取样频率是Bo 4 kHz C. 2 kHz Do 1 kHz44.设系统的零状态响应ty zs(t) f( )d,那么该系统是A.稳定的Bo不稳定的Co非因果的Do非线性的45. Sa[ (t 4)] (t 4〕等于A. (t 4) Bosin (t 4) Co 1 Do 0 46.连续周期信号的频谱有〔A.连续性、周期性Co离散性、周期性Bo Do连续性、收敛性离散性、收敛性47.某信号的频谱密度函数为F(j ) 2 )]e j3,那么f(t)A. Sa[2 (t 3)] Bo 2Sa[2 (t 3)]C. Sa(2 t) Do 2Sa(2 t)48.理想低通滤波器一定是〔A.稳定的物理可实现系统Bo稳定的物理不可实现系统C.不稳定的物理可实现系统Do不稳定的物理不可实现系统(s 3)e49 .单边拉氏变换F(s) -------------- 的原函数f(t)( )s 3Do e 3t (t 3)50 .当输入信号的复频率等于系统函数的零点时,系统的强迫响应分量为( )A.无穷大Bo不为零的常数Co 0 Do随输入信号而定51 .欲使信号通过系统后只产生相位变化,那么该系统一定是( )A.高通滤波网络Bo带通滤波网络Co全通网络D.最小相移网络52 .信号f(t)的傅氏变换为F( j ,那么f(3 ；)的傅氏变换为( )A. 2F( j2 )e j3Bo 2F( j2 )e j3C. 2F( j2 )e j6Do 2F( j2 )e j653 .信号的时宽与信号的频宽之间呈( )A.正比关系Bo反比关系Co平方关系D.没有关系58 .某信号的频谱是周期的离散谱,那么对应的时域信号为( )A.连续的周期信号Bo连续的非周期信号C.离散的非周期信号Do离散的周期信号59 .假设线性时不变因果系统的频率响应特性H(j ),可由系统函数H(s)将其中的s换成j 要求该系统函数H (s)的收敛域应为( )A. Re[s]＞某一正数BoRe[s] ＞某一负数C. Re[s]V某一正数Do Re[s]V某一负数60.对于某连续因果系统,系统函数H(s)； 2 2 .—,,一一,下面说法不对的是(3(t 1)A. e (t 1) Bo3(t 3)e (t 3)3t C. e (t 1)54 .时域是实偶函数,其傅氏变换一定是A.实偶函数Bo纯虚函数55 .幅度调制的本质是( )A.改变信号的频率C.改变信号频谱的位置)Co任意复函数D.任意实函数Bo改变信号的相位Do改变信号频谱的结构56 .假设f(t) h(t) y(t),那么f(3t) h(3t)A. y(3t) Bo 3 y(3t)1 …,t、C y(3t) D.y(二)3 357 .假设信号f[(t)的奈奎斯特取样频率为 1 , f 2 (t)的奈奎斯特取样频率为2,且1> 2,那么信号f (t) f1 (t 1)f2(t 2)的奈奎斯特取样频率为(Bo Co Do 1 2来求取,那么61.以下信号分类法中错误的选项是()68.以下为4个信号的拉普拉斯变换,其中不存在傅里叶变换的信号是()A. 1Bo 1 Co -^―Do ~^—s s 2 s 2f(t)的作用下的零状态响应为y zs(t) f(4t),那么该系统为()A.线性时不变系统Bo线性时变系统C.非线性时不变系统D.非线性时变系统5_70.f(t)是周期为T的函数,f(t)— f(t 3T)的傅里叶级数中,只可能有( )A.正弦分量Bo余弦分量Co奇次谐波分量D.偶次谐波分量3t t ................其在某鼓励信号作用下的自由响应为(e e ) (t),强迫响应为(1 e 2t) (t),那么下面的说法正确的选项是()A.该系统一定是二阶系统B o该系统一■定是稳定系统A.这是一个一阶系统C.这是一个最小相位系统B.这是一个稳定系统D.这是一个全通系统A.确定信号与随机信号B. 周期信号与非周期信号C.能量信号与功率信号62.以下各式中正确的选项是(A. (2t) (t)；;1C. (2t) - (t)2 D. 一维信号与二维信号)B. (2t) 2 (t)；1D.2 (t) - (2t)263 .以下关于傅氏变换的描述的不正确的选项是A ..时域周期离散,那么频域也是周期离散的; ()B时域周期连续,那么频域也是周期连续的； C.时域非周期连续,那么频域也是非周期连续的； D.时域非周期离散,那么频域是周期连续的._ . ............ .... .. ....... ..... ... . ,一1 ,64 .假设对f(t)进行理想取样,其奈奎斯特取样频率为f s,对f(-t3 率为()A. 3 f s Bo 1 f s C.3 ( f s -2)3 2)进行取样,其奈奎斯特取样频1,•〜65 . f1(t 5) f2 (t 3)等于(A. f1 (t) f2(t) Bo f1 (t) f2(t 8)C. f1(t) f2(t 8)566 .积分(t 3) (t 2)dt 等于(5 'A. - 1 Bo 167 .某连续时间系统的系统函数Do f1(t 3) f2(t 1))Co 0 D.一0.51 、一、『八,,H(s) ——,该系统属于什么类型() s 1A.高通滤波器Bo低通滤波器Co带通滤波器Do带阻滤波器69.一连续系统在输入71 . 一个线性时不变的连续时间系统,C.零输入响应中一定包含(e 3t e t ) (t) Do 零状态响应中一定包含(1 e 2t ) (t).信号f(t)的最高频率f o (Hz),那么对信号f(；)取样时,其频谱不混迭的最大奈奎斯特取样间隔T m ax 等于( ) A. 1/f . B. 2/f .C. 1/2f 0Do 1/4f 0・脉冲信号f(t)与2 f (2t)之间具有相同的是()A.频带宽度 Bo 脉冲宽度 Co 直流分量 Do 能量_ d .......... 一..・函数f(t) 一 (t 2)的单边拉氏变换 F(s)等于() dt1 - 1 2s_2sA. 1 Bo - C .一eD .es s.某系统的系统函数H (s),唯一决定该系统冲激响应 h(t)函数形式的是()A. H(s)的零点 Do 鼓励与H(s)的极点H (s)的共轲极点在虚轴上,那么它的 h(t)应是()A .指数增长信号B .指数衰减振荡信号C .常数D .等幅振荡信号.一连续系统的零极点分别为一2, -1, H ( ) 1 ,那么系统函数 H(s)为( )s 1 _ s 2 s 2A. ------- Bo -------------------------- Co (s 1)(s 2)Do ------s 2 s 1s 1.信号e j2t (t)的傅氏变换是( )A. 1 Bo j( 2) Co 0D .j(2 )・关于连续时间系统的单位冲激响应,以下说法中错误的选项是()2t.一个LTI 系统的初始无储能,当输入 x/t)(t)时,输出为y(t) 2e 2t (t)+ (t),当输入x(t) 3e t (t)时,系统的零状态响应 y(t)是()72 7374 75 76777879808182Bo H(s)的极点C.系统的鼓励.某二阶LTI 系统的频率响应 H(j )j 2 (j ) 3j那么该系统具有以下微分方程形式2A. y 2y 3y f 2 C. y 3y 2y f 2f.连续周期信号的傅氏变换是( A.连续的 Bo 周期性的Bo y 3y 2y f 2Do y 3y 2y f 2Co 离散的 Do 与单周期的相同.如果一连续时间二阶系统的系统函数 A.系统在 (t)作用下的全响应 B .系统函数H(s)的拉氏反变换C.系统单位阶跃响应的导数Do 单位阶跃响应与 (t)的卷积积分A. ( 9e t 12e 3t) (t) Bo (3 9e t 12e 3t) (t)C. (t) 6e t (t) 8e 2t (t) Do 3 (t) 9e t (t) 12e 2t (t)83.以下的连续时间信号,哪个不是周期信号?A. f (t) 3cos(4t /3) Bo f(t) e j(t "C. f (t) cos(2t /3)2Do f(t) e2t84 .连续时间信号f(t)[sin(100t)/50t] cos(1000t),该信号的频带为(A. 100 rad / sB. 200 rad / s Co 400 rad / s Do 50 rad /s85 .信号sin( 0t) (t)的傅氏变换是()(/j)[( 0)( 0)] Bo 0)( 0)]C. (/2j)[( 0)] + 0/( 2)D. [( 0) 0)] + 0 /(2)86.满足狄里赫利收敛条件时,傅氏级数与原周期信号f(t)之间(A.处处相等Bo只能保证傅氏级数系数有界C.除f (t)不连续的t值外,处处相等Do处处不相等,但能量相同87.满足傅氏级数收敛条件时,周期信号f(t)的平均功率()A.大于各谐波分量平均功率之和C.小于各谐波分量平均功率之和Bo不等于各谐波分量平均功率之和Do等于各谐波分量平均功率之和88. 假设f(t)为实信号,以下说法中不正确的选项是(89. A.该信号的幅度谱为偶对称C.该信号的频谱为实偶信号理想低通滤波器是( )A.物理可实现的Bo非因果的BoDo该信号的相位谱为奇对称该信号的频谱的实部为偶函数,虚部为奇函数Co因果的Do 不稳定的90. sin( 0t) (t)的拉氏变换为()A. ( /2)[ 0) ( 0)] Bo0)( 0)]C. s/(s202) Do 0/(s291 .连续时间信号f(t)的拉氏变换的收敛域是A.带状B.环状Co与无关Do与变量有关92.一LTI系统对f (t)的y zs(t)4 df(t 2),那么该系统函数dt(s)为, 2sBo 4se Co 4F(s)e 2s Do 2s .4e / s93 .单边拉氏变换 F(s)= 1+ s 的原函数94 .以下表达正确的选项是() A.各种数字信号都是离散信号 C.数字信号的幅度只能取1或0Bo 各种离散信号都是数字信号 Do 将模拟信号抽样直接可得数字信号95 .信号f(t) 3cos(4t / 3)的周期是97.离散时间单位延迟器 D 的单位序列响应为二、填空题1 . f(t t 1) (tt 2)2 .从信号频谱的连续性和离散性来考虑,周期信号的频谱是 3.符号函数sgn(2t 4)的频谱函数F(j co )= 4.频谱函数F (j co )=( G -2)+ S ( co +邱傅里叶逆变换f (t)=5.一线性时不变系统,在鼓励信号为f (t)时的零状态响应为y zs (t),那么该系统的系统 函数H(s)为.6.对于一个三阶常系数线性微分方程描述的连续时间系统进行系统的时域模拟时,所需积分器数目最 少是 个.A.(t)⑴B . e t (t) Co (t 1) (t)Do (1 e t ) (t)A. (k)B .(k 1)Co(k 1)D .98. f(t) (t 2n)周期信号的傅立叶变换为n ) Bo 2nC o99. (k)可写成以下正确的表达式是(A. (k)(n)nBo100. C . (k) (k) (k 1) (k)(k 1)(k 1) (k) Bo k (k 1) 2nDo 0.5(k)(k) C . (k 1) (k n(k) (k) n)(k Do 1)(k 1)(k 1)处为()A. 2BoCo/2 Do /496.以下系统函数表达式中,是稳定全通系统H(s)的是(,3 j —(s 1)(s e 4 )(s e A. H (s)(s ―)(s —e-)(s —ej-,3 j —4)j-B .H(s)(s,3 j-1)(s e 4)(s ,3 j —4)C. H(s)(s 1)(s e 4)(s e 4) (s 1)(s e 4)(s e 4),3. 3j j-(s 1)(s e 4)(s e 4)D .H(s)j-j-(s 1)(s e 4)(s e 4)(s 1)(s e )4)(s e 4)(sj -1)(s e 4)(s,36)7.一线性时不变连续因果系统是稳定系统的充分且必要条件是系统函数的极点位于S平面的8 .如果一线性时不变系统的单位冲激响应为h(t),那么该系统的阶跃响应g⑴为9 .如果一线性时不变系统的输入为f(t),零状态响应为y zs(t) 2f(t t o),那么该系统的单位冲激响应h(t)为.10 .如果一LTI系统的单位冲激响应h(t) (t),那么当该系统的输入信号f(t) = t (t)时,其零状态响应为.11 .x(t)的傅里叶变换为X (j G),那么x(t t°)的傅里叶变换为.12 . x1(t) (t t0), x2(t)的频谱为疝8 (" 8 (n⑼],且y(t) x1(t) x2(t),那么y(t0)=________________ o13 .假设f1⑴的拉氏变换F I (s) =1/s ,那么f (t)=f1(t) f1(t)的拉氏变换F (s) =.14 .线性时不变系统的冲激响应为h(t) = (1 e t) (t),那么其系统函数H (s) =.215 .一信号f(t)的频谱F(j )的带宽为1,那么f 2(2t)的频谱的带宽为.1 …一、,一,、一 1 一一、一、一一16 .一离散时间系统的系统函数H(z) ------------ 1 --------- 2,判断该系统是否稳定.2 z z117 .某因果系统的系统函数为H(s) ------------------------- ,要使系统稳定,那么k值的范围为s (3 k)s k18 . sin t (t) __________________19 .积分器的频域系统函数H (j )=.20 .信号不失真的条件为系统函数H (j )=.2t -21 . e (t) (t 3) _____________________________22.0 Sa(t)dt 等于23 .阶跃信号(t)与符号函数sgn(t)的关系是24 .偶周期信号的傅氏级数中只有 ____________________________________25 .如果系统的单位冲激响应为h(t),那么该系统函数H(s)为26.如果一个系统的幅频响应H(j )是常数,那么这个系统就称为27 .单位冲激.信号的拉氏变换结果是28 .在收敛坐标0 的条件下,系统的频率响应和系统函数之间的关系是把系统函数中的s用j代替后的数学表达式.29 .系统函数零点全在左半平面的系统称为.30 . H (s)的零点和极点中仅决定了h (t)的函数形式.31 .系统的冲激响应是阶跃响应的.32.斜升函数t (t)是(t)函数的______________________ -33.系统的初始状态为零,仅由引起的响应叫做系统的零状态响应.34.鼓励为零,仅由系统的引起的响应叫做系统的零输入响应.35.系统对f(t)的响应为y(t),假设系统对f(t—t o)的响应为y (t —t o),那么该系统为系统.36.系统的全响应可分解为零输入响应与零状态响应两局部响应之和,又可分解为响应及强迫响应两局部响应之和.37.非周期连续信号的频谱是的.38.信号的拉普拉斯变换F (s) 2 3e s 4e 2s,其原函数f (t)为39 .LTI系统的频率响应函数H(j ) —k^——1)一,假设H(0) 1,那么卜= (j 2)( j 3) ——40 .因果系统是物理上系统.41 .某一因果连续时间LTI系统的频率响应为H (j ),那么该系统对输入信号f(t)=E a〔e j 0t a 隹j 0t的响应y(t)为.42 .频谱X() (),那么其傅氏反变换x(t) =.43 .设某一周期锯齿脉冲信号的傅氏级数的系数为ak,当k 时,ak = .44 .因果连续时间LTI系统H(j )对(t)的稳态响应为.45 .信号在时域拥有的总能量,等于其频谱在频域内能量的.46 .当用傅氏级数的有限项和来近似表示信号时,在信号的断点处存在.47,连续时间LTI系统对周期信号的响应为.1 _48 .信号的拉氏变换为F(s) [ -------------------- ,那么该信号的傅氏变换F(j ) .(s2 1)(s 1)49 .一离散时间LTI系统的单位阶跃响应g(k) (0.5)k (k),那么该系统的单位序列响应h(k) .50 .假设离散时间系统的单位序列响应h(k) (k) (k 2),那么系统在f(k) {1, 2, 3},k 1,2,3鼓励下的零状态响应为.三、判断题：(正确的打,错误的打“x〞)1 .f1(t) (t 1) (t 1), f2(t) (t 1) (t 2),那么f1(t) f2(t)的非零值区间为10,3]o( )2 .假设L [ f (t)] = F (s),那么L [ f (t t.)] = e st°F(s).()3 .奇函数加上直流后,傅氏级数中仍含有正弦分量. ()1 e s/ 、4 . L --------- 2- sin(t 1). ( )1 s5 . 一个系统的零状态响应就等于它的自由响应. ()6 .假设系统起始状态为零,那么系统的零状态响应就是系统的强迫响应. ()7 . H (s)的零点与h(t)的形式无关.()8 .假设一个连续LTI系统是因果系统,它一定是一个稳定系统. ()9 .因果连续LTI系统的系统函数的极点一定在s平面的左半平面.()10 . 一个信号存在拉氏变换就一定存在傅氏变换. ()11 .周期连续时间信号,其频谱是离散的非周期的. ()12 .稳定系统的H (s)极点一定在s平面的左半平面.()13 .因果稳定系统的系统函数的极点一定在s平面的左半平面.()14 .任意系统的H(s)只要在s处用j代入就可得到该系统的频率响应H(j ).()15 .系统的h(t)是由其系统函数H(s)的零极点位置决定的.()16 .假设y(t) f(t) h(t),那么y( t) f ( t) h( t).()17 .假设y(t) f(t) h(t),那么y(t 1) f (t 2) h(t 1).()18 .零状态响应是指系统没有鼓励时的响应. ()15 / 2415 / 2419 .非周期的冲激取样信号,其频谱是离散的、周期的. 〔〕20 . 一个系统的自由响应就等于它的零输入响应. 〔〕21 .用有限项傅里叶级数表示周期信号,吉布斯现象是不可防止的. 〔〕22 .对连续周期信号取样所得的离散时间序列也是周期信号. 〔〕23 .理想模拟低通滤波器为非因果物理上不可实现的系统. 〔〕24 .拉普拉斯变换满足线性性质. 〔〕25 .拉普拉斯变换是连续时间系统进行分析的一种方法.〔〕26 .假设信号是实信号,那么其傅里叶变换的相位频谱是偶函数. 〔〕27 .单位阶跃响应的拉氏变换称为系统函数.〔〕28 .系统的极点分布对系统的稳定性是有比拟大的影响的.〔〕29 .信号时移只会对幅度谱有影响. 〔〕30 .在没有鼓励的情况下,系统的响应称为零输入响应. 〔〕31 .抽样信号的频率比抽样频率的一半要大. 〔〕32 .只要输入有界,那么输出一定有界的系统称为稳定系统. 〔〕33 .时不变系统的响应与鼓励施加的时刻有关. 〔〕34 .信号3e 2t〔t〕为能量信号.〔〕35 .信号e t cos10t为功率信号.〔〕36 .两个周期信号之和一定是周期信号. 〔〕37 .所有非周期信号都是能量信号. 〔〕38 .卷积的方法只适用于线性时不变系统的分析. 〔〕39 .两个线性时不变系统的级联构成的系统是线性时不变的. 〔〕40 .两个非线性系统的级联构成的系统也是非线性的. 〔〕41 .假设一个系统的H〔s〕的极点多于零点,且该系统是因果的,那么其阶跃响应在t 0上是连续的.〔〕42 . 一个因果的稳定系统的系统函数H〔s〕所有的零、极点必须都在S平面的左半平面内.〔〕43 .离散信号经过单位延迟器后,其幅度频谱也相应延迟. 〔〕44 . —〔t2 sin t〕是周期信号. 〔〕dt45 .一系统的H〔s〕后,可以唯一求出该系统的h〔t〕o 〔〕46 .没有信号可以既是有限时长的同时又有带限的频谱. 〔〕47 .假设y〔t〕 f〔t〕 h〔t〕,那么y〔2t〕 2f〔2t〕 h〔2t〕.〔〕48 .两个奇信号相加构成的信号一定是偶对称的. 〔〕参考答案单项选择题:1.B2.D3.C4.B5.A6.C16.B17.D18.C19.B20.C 31.B32.B33.D34.B35.D 46.D47.B48.B49.C50.C55.C56.C57.C58.D59.B 68.D69.B70.C71.B72.A 81.A82.D83.D84.B85.C 94.A95.C96.B97.C98.A21.B36.A51.C60.C73.C86.C99.D7.A 8.B 9.C22.A37.B52.D61.D74.D87.D100.B10.A 11.D 12.B 13.B 14.C 15.D填空题1. f(t t1 t2 ) .2.o 离散的.3.6. 3 个.7. 左半平面. 8.t0X(j 〕.12.1 .16.系统不稳定. 17.0< k<3.2(t 3)21. e ( ) (t 3) 22.23.A38.C24.C39.B25.B40.D26.A41.C27.C42.B28.A 29.A43.B 44.B30.B45.A53.B 54.A62..C 63.B 64.B 65.D 66.A 67.B75.B 76.C 77.C 78.D 79.D 80.A88.C 89.B 90.D 91.A 92.B 93.AAeh( )d j24. 5.y zs⑴L f(t)9.〔t t.〕. 10.(t)13.y 218 . (t)14.19.15.4s(s 1)20.ke j t0 23.sgn(t) 2 (t) 24.直流项和余弦项25.L [h 〔t〕].31.一阶导数. 26.全通系统27.37. 连续的.EH(j0)l t im y(t)32.二次积分.38. 2 (t)a1e j 0t H (jH(j0)k k49. (0.5) (k) (0.5)(t 三、判断题:1.,2. 14. X 15 24. V 25 34. V 35 X 3 V z 416263645.(k1727a 1e总和28.33.输入.1) 4 (tj 0t H ( j29.最小相位系统.34.初始状态.35.时不变.30.极点36.自由响应.2).39. 6.40.可实现的.0) 4246.吉布斯现象(t)/2 1/2tj 43.047.周期信号48. 小存在1) 50.f(k) h(k) {1,2,3} {1,1} {1,3,5,31 , k=1,2,3,4X 28o V 37 o X 38 o7v z 8.X 9.X 10.x 19 o xo V 29 o XV 39 o V 402030o x2111 o V 12 o 义3141.13.V..义 32 o V 33 o XV 42 o X 43 o X 44 o V 45 .X 46.信号与系统综合复习资料测试方式：闭卷测试题型：1、简做题(5个小题),占30分；计算题(7个大题),占70 分.一、简做题：1 . y(t) e t x(0) f(t)d"t)其中x(0)是初始状态, dtf(t)为鼓励,y(t)为全响应,试答复该系统是否是线性的？［答案：非线性］2 . y1(t) sinty(t) f (t)试判断该微分方程表示的系统是线性的还是非线性的,是时变的还是非时变的？［答案：线卜t时变的］3 .有限频带信号f(t)的最高频率为100Hz,假设对f(2t)* f(3t)进行时域取样,求最小取样频率f s = ?［答案：f s 400 Hz］4 .简述无失真传输的理想条件.［答案：系统的幅频特性为一常数,而相频特性为通过原点的直线］5 .求e 2t '(t) (t)dt 的值.［答案：3］6 .f(t) F(j ),求信号f (2t 5)的傅立叶变换.心… 1 5j［答案：f (2t 5) -e2 F(j-)］2 27.f(t)的波形图如下图,画出 f (2 t) (2 t)的波形.8 .线性时不变系统,当输入x(t) (e3t) (t)时,其零状态响应为y(t) (2e t 2e 4t) (t),求系统的频率响应.［答案(j 3) 2j 5(j 2)( j4)]_ ___ 2s 39.求象函数F(s) s2,的初值f(0 )和终值f ((s 1)2［答案:f(0 )=2, f( )0] 10.假设LTI离散系统的阶跃响应为g(k),求其单位序列响应.其中：g(k)(2)(k)[答案：h(k) g(k) g(k 1) 9k(k) 1 k 1(2)(k 1)(k)1 k(2) (k 1)]1 , k 0,1,211.f1 k0 , else f21 , k 0,1,2,30 , else设f k f1k f2k ,求［答案：3］12.描述某离散系统的差分方程为 1 2y k 2 f (k)求该系统的单位序列响应h k.［答案: h(k) 2 L 1曰2)3](k)]13 .函数f t的单边拉普拉斯变换为2t 3e f 3t的单边拉普拉斯变s 2换.[答案：Y s ^^]s 514.f1 t、f2 t的波形如以下图,求f1 t f2 t (可直接画出图形)f1 tf2 t15.有一线性时不变系统,当鼓励f 1(t) (t)时,系统的响应为 y(t) e t (t);试求：当鼓励f 2(t) (t)时的响应(假设起始时刻系统无储能) .[答案：y 2(t)y'(t) [e t (t)]' e t (t) e t (t) e t (t)(t)]二、某LTI 连续系统,其初始状态一定,当鼓励为f(t)时,其全响应为y i (t) e t cos t,t 0;假设初始状态保持不变,鼓励为2 f (t)时,其全响应为 y 2 (t) 2cos( t),t 0；求：初始状态不变,而鼓励为[答案：y 3⑴y x (t) 3y f (t) 2e t 3( e t cos t)、描述LTI 系统的框图如下图[答案:f(t)3 f (t)时系统的全响应. e t 3cos t,t 0]假设 f(t) e t (t), y(0 ) 1,y'(0 ) 2,求其完全响应 y(t).3t 4t 3t8 4t 1 ty(t) y x (t) y f (t) 6e 5e 3e -e e[答案：33]3t23 4t 1 t.[9e —e -e ] (t)3 3四、图示离散系统有三个子系统组成,h i (k)f (k) (k) a (k 1),求：零状态响应 y f (k)0k[答案：2cos —] 4五、描述系统输入f (t)与输出y(t)的微分方程为:y''(t) 5y'(t) 6y(t) f'(t) 4f(t)s 4 a)写出系统的传递函数；[答案：H(s) 2 ]s 5s 6b)求当f (t) e t (t), y'(0 ) 1,y(0 )0时系统的全响应[答案：y(t) (3e t e 2tl e 3t ) (t)]2 2六、因果线性时不变系统的输入 f(t)与输出y(t)的关系由下面的微分方程来描述：d y(t) 10y(t) f( )z(t )d f (t)dt一 ,k 、. . k2cos(——),h 2(k) a 4(k),鼓励求：该系统的冲激响应 ［答案：h(t) 2 t 十一 0一-、,1 或：h(t) ( e9-sin tcos1000t[答案： -------------2 t八、求以下差分方程所描述的离散系统的零输入响应、零状态响应.九、求以下象函数的逆变换:(1)写出描述系统的微分方程;(2)求当 f(t) (t),y'(0 ) 1,y(0 )0 时系统的零状态响应和零输入响应.[答案：(1) y (t) 3y (t)2y(t) f (t)4f(t)(2) y x (t) (e t 2t) (ty f (t) (2 2te3e t ) (t)I ^一、一个因果 LTI 系统的输出y(t)与输入 f(t)有以下微分方程来描述:17 10t 、e ) (t)]七、图(a)所示系统,其中f(t) sn 22 ts(t) cos(1000t),系统中理想带通滤波器的频y(k) f(k)3y(k 1) 2y(k 2) f (k) (k),y( 1) l,y(2) 0［答案:y x (k) [( 1)k4( 2)k] (k),1 k 4 k 1y f(k)[ 2(1)3(2)6](k)]1(s 1)(s 4)s(s 2)(s 3)2、F(s)s 2 4s 5 s 2 3s 2[答案：(1) f (t)(32t3t)(2) f(t)(t) (2e t2te )(t)]十、系统的传递函数H(s)s 4 s 2 3s 2率响应如图(b)所示,其相频特性 (t 0])0,求输出信号y(t)0(1)确定系统的冲激响应h(t)； (2)假设f(t) e 2t (t),求系统的零状态响应y f (t) [答案：(1) h(t) (e 2t e 4t ) (t)11 ⑦⑵ y f (t) ( e 4t (t )e 2t ) (t)]22十二、某LTI 系统的输入为：f(k)求系统的单位序列响应h(k) 0十三、某LTI 系统,当输入为f(t) ey f (t) (e t 2e 2t 3e 3t ) (t)求系统的阶跃响应 g(t).[答案：g(t) (1 e 2t 2e 3t ) (t)] 十四、某LTI 系统,其输入f(t)与输出y(t)的关系为：2(t x),y(t) t1e f (x 2)dx求该系统的冲激响应.[答案：h(t) e 2(t 2) ( t 3)]十五、如题图所示系统,他有几个子系统组合而成,各子系统的冲激响应分别为：h a (t) (t 1) h b (t)(t) (t 3)求：复合系统的冲激响应.[答案：h(t) (t) (t 1) (t 2) (t 3) (t 4) (t 5)]1,k 04,k 1,2时,其零状态响应y(k) 0,k 0 ,9,k 00,其余[答案：h(k) [1 (6kk8)( 2) ] (k)]六、ft的频谱函数F j 1, 2 rad /s,那么对f 2t进行均匀抽样,为使抽0, 2 rad /s样后的信号频谱不产生混叠,最小抽样频率应为多少？[答案：4HZ]十七、描述LTI系统的微分方程为y (t) 3y(t) 2y(t) f(t) 4f(t)f (t) (t) , y(0 ) 1 , y(0 ) 3,求系统的零状态响应和零输入响应.[答案：y x(t) (4e t 3e,(t) y,(t) (2 3e t e2t) (t)]。

一、单项选择题：14、已知连续时间信号,)2(100)2(50sin )(--=t t t f 则信号t t f 410cos ·)(所占有的频带宽度为（） A ．400rad ／s B 。

200 rad ／s C 。

100 rad ／s D 。

50 rad ／s15、已知信号)(t f 如下图（a ）所示，其反转右移的信号f 1(t) 是（ ）16、已知信号)(1t f 如下图所示，其表达式是（ ）A 、ε（t ）＋2ε(t －2)－ε(t －3)B 、ε(t －1)＋ε(t －2)－2ε(t －3)C 、ε(t)＋ε(t －2)－ε(t －3)D 、ε(t －1)＋ε(t －2)－ε(t －3)17、如图所示：f （t ）为原始信号，f 1(t)为变换信号，则f 1(t)的表达式是（ ）A 、f(－t+1)B 、f(t+1)C 、f(－2t+1)D 、f(－t/2+1)18、若系统的冲激响应为h(t),输入信号为f(t),系统的零状态响应是（ ）19。

信号)2(4sin 3)2(4cos 2)(++-=t t t f ππ与冲激函数)2(-t δ之积为（ ）A 、2B 、2)2(-t δC 、3)2(-t δD 、5)2(-t δ，则该系统是（）＞－系统的系统函数．已知2]Re[,651)(LTI 202s s s s s H +++= A 、因果不稳定系统 B 、非因果稳定系统C 、因果稳定系统D 、非因果不稳定系统21、线性时不变系统的冲激响应曲线如图所示，该系统微分方程的特征根是（ ）A 、常数B 、 实数C 、复数D 、实数+复数22、线性时不变系统零状态响应曲线如图所示，则系统的输入应当是（ ）A 、阶跃信号B 、正弦信号C 、冲激信号D 、斜升信号23. 积分⎰∞∞-dt t t f )()(δ的结果为( )A )0(fB )(t f C.)()(t t f δ D.)()0(t f δ24. 卷积)()()(t t f t δδ**的结果为( ) A.)(t δ B.)2(t δ C. )(t f D.)2(t f25. 零输入响应是( )A.全部自由响应B.部分自由响应C.部分零状态响应D.全响应与强迫响应之差2A 、1-eB 、3eC 、3-e D 、127.信号〔ε(t)－ε(t －2)〕的拉氏变换的收敛域为 ( )A.Re[s]>0B.Re[s]>2C.全S 平面D.不存在28．已知连续系统二阶微分方程的零输入响应)(t y zi 的形式为t t Be Ae2--+，则其2个特征根为( ) A 。

第1 页（共4 页）《信号与系统》须知：符号e (t)(t)、、e (k)(k)分别为单位阶跃函数和单位阶跃序列。

分别为单位阶跃函数和单位阶跃序列。

LTI 表示线性时不变。

为加法器。

一、单项选择题（每小题4分，共32分）D 1、序列和33(2)ii i d ¥-=-¥-å等于A ．3e (k –2)B ．3e (k)C ．1D ．3 D 2、积分55(1)d 2t t e t d --ò等于A ．0B ．1C ．eD ．e 2 B 3、()(a )f t t d =A ．(0)f t d()B ．1(0)()|a |f t d C ．(0)f aD ．0()f t a æöd ç÷èøB 4、1()f t 、2()f t 波形如题4图所示，12()()*()f t f t f t =则(2)f =t1()f t -22240t2()f t 11-120题4图A ．12B ．1C ．32D ．2 B 5、已知)()()(21k f k f k f *=，)(1k f 、)(2k f 波形如题5图所示，)0(f 等于1()f k 012312()f k 011-11kk题5图A ．1B ．2C ．3D ．4 D 6、已知()1sgn()f t t =+则其傅立叶变换的频谱函数()F j w 等于A ．12()j pd w +w B ．2j wC ．1()j pd w +wD ．2()j 2pd w +w∑D 7、已知单边拉普拉斯变换的象函数22()1F s s =+则原函数)(t f 等于等于A ．()te t -e B ．2()te t -e C ．2cos ()t t e D ．2sin ()t t e B 8、已知)()(k k kf e =，其双边Z 变换的象函数)(z F 等于等于 A ．1-z z B ．2)1(-z z C ．1--z z D ．2)1(--z z二、填空题（每小题5分，共30分）分） 9、单边拉普拉斯变换定义()F S =0()stf t e dt-¥-ò；双边Z 变换定义式()F Z =()kk f k z¥-=-¥å10、已知()f t 的波形如题10图所示，则(12)f t -波形波形 (1) ；()df t dt波形波形(2) 。

信号与系统期末考试试题有答案信号与系统期末考试试题一、选择题（共10题，每题3分，共30分，每题给出四个答案，其中只有一个正确的）1、卷积f1(k+5)*f2(k-3)等于。

（A）f1(k)*f2(k)（B）f1(k)*f2(k-8)（C）f1(k)*f2(k+8)（D）f1(k+3)*f2(k-3)2、积分等于。

（A）1.25（B）2.5（C）3（D）53、序列f(k)=-u(-k)的z变换等于。

（A）（B）-（C）（D）4、若y(t)=f(t)*h(t),则f(2t)*h(2t)等于。

（A）（B）（C）（D）5、已知一个线性时不变系统的阶跃相应g(t)=2e-2tu(t)+,当输入f(t)=3e—tu(t)时，系统的零状态响应yf(t)等于（A）(-9e-t+12e-2t)u(t)（B）(3-9e-t+12e-2t)u(t)（C）+(-6e-t+8e-2t)u(t)（D）3+(-9e-t+12e-2t)u(t)6、连续周期信号的频谱具有（A）连续性、周期性（B）连续性、收敛性（C）离散性、周期性（D）离散性、收敛性7、周期序列2的周期N等于（A）1（B）2（C）3（D）48、序列和等于（A）1(B)∞(C)(D)9、单边拉普拉斯变换的愿函数等于10、信号的单边拉氏变换等于二、填空题（共9小题，每空3分，共30分）1、卷积和[（0.5）k+1u(k+1)]*=________________________2、单边z变换F(z)=的原序列f(k)=______________________3、已知函数f(t)的单边拉普拉斯变换F(s)=，则函数y(t)=3e-2t·f(3t)的单边拉普拉斯变换Y(s)=_________________________4、频谱函数F(j)=2u(1-)的傅里叶逆变换f(t)=__________________5、单边拉普拉斯变换的原函数f(t)=__________________________6、已知某离散系统的差分方程为，则系统的单位序列响应h(k)=_______________________7、已知信号f(t)的单边拉氏变换是F(s),则信号的单边拉氏变换Y(s)=______________________________8、描述某连续系统方程为该系统的冲激响应h(t)=9、写出拉氏变换的结果，三、（8分）四、（10分）如图所示信号，其傅里叶变换，求（1）（2）六、（10分）某LTI系统的系统函数，已知初始状态激励求该系统的完全响应。