材料力学(静不定)

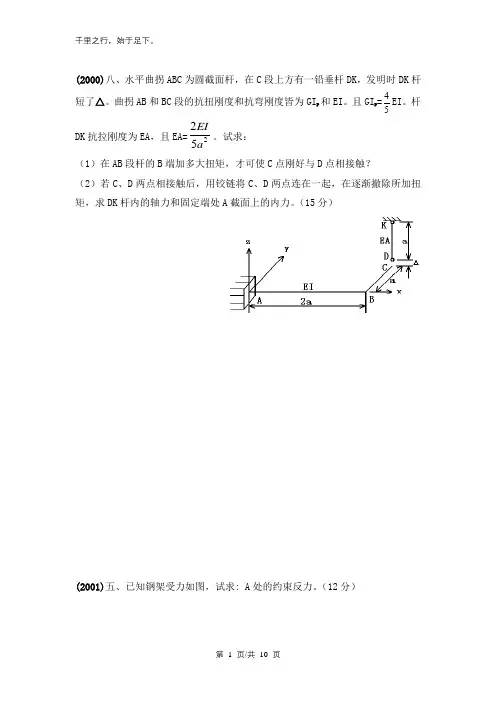
第 1 页/共 10 页(2000)八、水平曲拐ABC 为圆截面杆，在C 段上方有一铅垂杆DK ，发明时DK 杆短了△。

曲拐AB 和BC 段的抗扭刚度和抗弯刚度皆为GI P 和EI 。

且GI P =45EI 。

杆DK 抗拉刚度为EA ，且EA=225EIa 。

试求：（1）在AB 段杆的B 端加多大扭矩，才可使C 点刚好与D 点相接触？ （2）若C 、D 两点相接触后，用铰链将C 、D 两点连在一起，在逐渐撤除所加扭矩，求DK 杆内的轴力和固定端处A 截面上的内力。

（15分）(2001)五、已知钢架受力如图，试求: A 处的约束反力。

（12分）(2002)七、圆截面杆AB、BC的直径、材料均相同，已知：p、a，E=2.5G，且CD杆的EA=2EI/5a2，试求：CD杆的内力。

（12分）(2003)五、圆截面平面曲拐OAB与直杆CD直径、材料均相同。

已知P、L，且=0.8EI，EA=0.4EI/L2，求O端的约束反力。

（20分）GIp第3 页/共10 页(2004)三、已知平面曲拐ABC和DF梁的抗弯刚度为EI、抗扭刚度为GI和CD杆p=2EAL2。

试求CD杆的内力。

（20分）的抗拉刚度为EA，设EI=4GIP(2023年年)二、结构受力如图所示，已知平面钢架ABCD的抗弯刚度为EI，EF 杆的抗拉刚度为EA，设3EI=EAL2。

试求E、F两点的相对位移。

（20分）第5 页/共10 页(2023年年)八、已知平面钢架EI为常数，试问：若在C处下端增强一刚度为K=3EI/A3（单位：N/M）的弹性支座后，该钢架的承载能力（强度）将提高多少倍？（20分）第 7 页/共 10 页(2023年年)七、求BC 杆的内力，设2/EA EI a 。

（20分）(08.3)(2023年年)三、平面直角曲拐ABC和CD杆均为圆截面，材料相同，已知：3EI=GIp，第9 页/共10 页3EI=EAL2，试求CD杆的内力。

物体系统的平衡静定与静不定（超静定）问题•静定与超静定（静不定）的概念对每一种力系而言,若未知量的数目等于独立平衡方程的数目。

则应用刚体静力学的理论,就可以求得全部未知量,这样的问题称为静定问题。

（理论力学）若未知量的数目超过独立平衡方程的数目，则单独应用刚体静力学的理论,就不能求出全部未知量,这样的问题称为静不定问题（超静定问题）。

（材料力学等）静定：未知量个数等于独立的平衡方程数；未知量的数目=独立平衡方程的数目静不定(超静定)：未知量个数大于独立的平衡方程数。

未知量的数目> 独立平衡方程的数目超静定次数：未知量个数与独立的平衡方程数之差。

当研究对象中未知约束力个数小于独立的平衡方程数时，其运动状态一般都是变化的，工程中将这样的力学系统称为机构，这种情况在工程结构设计中是应该避免的。

具有n个物体组成的平面静定物体系统：最多3n个独立平衡方程，求解3n个未知量。

超静定问题：材料力学原理建立补充方程求解。

A BPF PF PF判断各图示结构的静定性•刚体系统（物体系统）的平衡问题1. 两个或两个以上刚体用一定的方式连接起来组成的系统，称为刚体系统；2. 刚体系统整体处于平衡时，每一局部均处于平衡。

局部：组成系统的单个或几个刚体所构成的子系统。

0A M =∑0D M =∑0C M =∑0B M =∑∑=0X 0=∑Y 刚体系统平衡问题的特点是：仅仅考察系统整体平衡，一般无法求得全部未知力。

1m 1m q pF F 1A 0.5m 0.5m (a)1m1m D B C Q Ax F Ay F M A BF P1.一般解法：编程，运用计算机求解线性代数方程组。

对于每个刚体都受平面任意力系作用的刚体系统，总可以建立3n个独立的平衡方程。

如果系统是静定的，也应有相同个数的未知量，最终就归结为求解线性代数方程组的问题，利用高斯消元法等方法，总能在计算机上程式化地实现数值求解。

2.分析解法：由于许多工程实际问题并不需要求出刚体系统的所有内部和外部的约束力，而通常只需求出某一部分的约束力，因此，利用分析解法以简化运算是必要的。

第十三章静不定问题分析§13-1 静不定结构概述1．定义用静力学平衡方程无法确定全部约束力和内力的结构或结构系统，统称为静不定结构或系统，也称为超静定结构或系统。

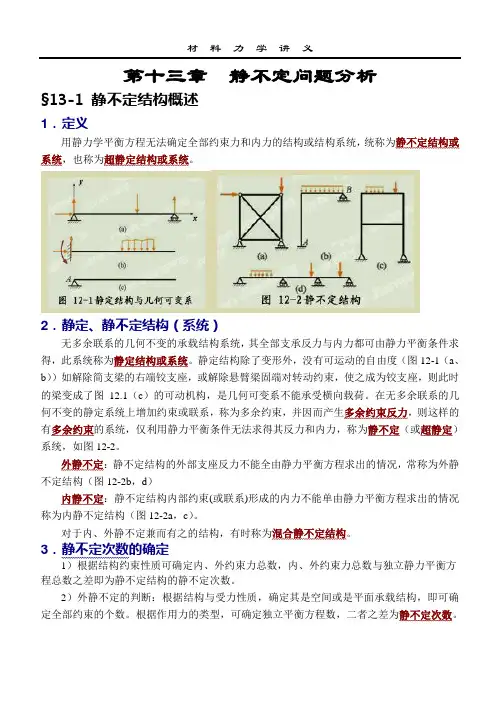
2．静定、静不定结构（系统）无多余联系的几何不变的承载结构系统，其全部支承反力与内力都可由静力平衡条件求得，此系统称为静定结构或系统。

静定结构除了变形外，没有可运动的自由度（图12-1（a、b））如解除简支梁的右端铰支座，或解除悬臂梁固端对转动约束，使之成为铰支座，则此时的梁变成了图12.1（c）的可动机构，是几何可变系不能承受横向载荷。

在无多余联系的几何不变的静定系统上增加约束或联系，称为多余约束，并因而产生多余约束反力，则这样的有多余约束的系统，仅利用静力平衡条件无法求得其反力和内力，称为静不定（或超静定）系统，如图12-2。

外静不定：静不定结构的外部支座反力不能全由静力平衡方程求出的情况，常称为外静不定结构（图12-2b，d）内静不定：静不定结构内部约束(或联系)形成的内力不能单由静力平衡方程求出的情况称为内静不定结构（图12-2a，c）。

对于内、外静不定兼而有之的结构，有时称为混合静不定结构。

3．静不定次数的确定1）根据结构约束性质可确定内、外约束力总数，内、外约束力总数与独立静力平衡方程总数之差即为静不定结构的静不定次数。

2）外静不定的判断：根据结构与受力性质，确定其是空间或是平面承载结构，即可确定全部约束的个数。

根据作用力的类型，可确定独立平衡方程数，二者之差为静不定次数。

如图12-3（b），外载荷为平面力系，则为三次外静不定静，而图12-3（c）为空间力系，则为六次外静不定。

3）内静不定次数确定桁架：直杆用铰相连接，载荷只作用于结点，杆只受拉压力的杆系，其基本几何不变系由三杆组成（图12-4a）。

图12-4（b）仍由基本不变系扩展而成，仍是静定系，而（c）由于在基本系中增加了一约束杆，因而为一次超静定。

刚架：杆以刚结点相连接，各杆可以承受拉、压、弯曲和扭转，这样的杆系为刚架（图12-5）。

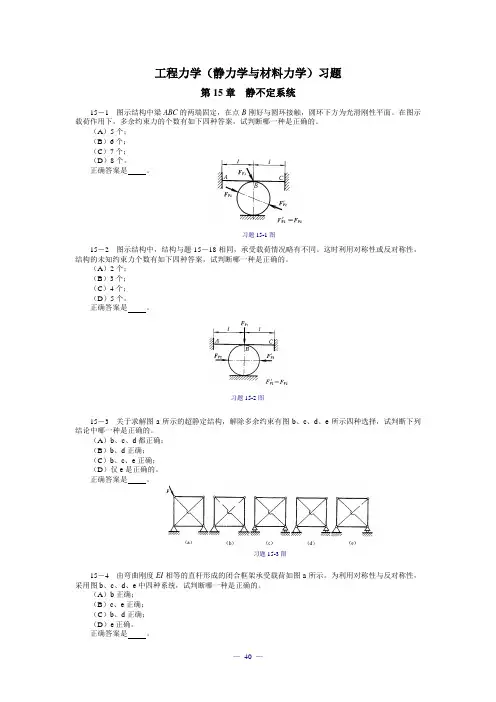
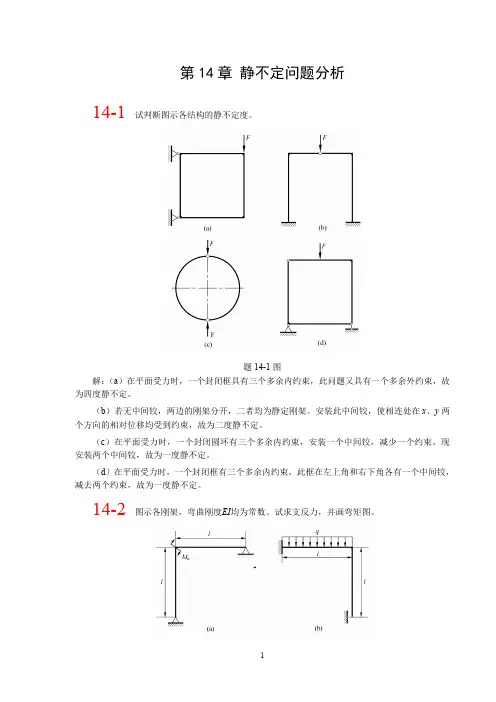
工程力学（静力学与材料力学）习题第15章静不定系统15－1 图示结构中梁ABC的两端固定，在点B刚好与圆环接触，圆环下方为光滑刚性平面。

在图示载荷作用下，多余约束力的个数有如下四种答案，试判断哪一种是正确的。

（A）5个；（B）6个；（C）7个；（D）8个。

正确答案是。

习题15-1图15－2 图示结构中，结构与题15－18相同，承受载荷情况略有不同。

这时利用对称性或反对称性，结构的未知约束力个数有如下四种答案，试判断哪一种是正确的。

（A）2个；（B）3个；（C）4个；（D）5个。

正确答案是。

习题15-2图15－3 关于求解图a所示的超静定结构，解除多余约束有图b、c、d、e所示四种选择，试判断下列结论中哪一种是正确的。

（A）b、c、d都正确；（B）b、d正确；（C）b、c、e正确；（D）仅e是正确的。

正确答案是。

习题15-3图15－4 由弯曲刚度EI相等的直杆形成的闭合框架承受载荷如图a所示。

为利用对称性与反对称性，采用图b、c、d、e中四种系统，试判断哪一种是正确的。

（A）b正确；（B）c、e正确；（C）b、d正确；（D）e正确。

正确答案是。

习题15-4图F’X习题15-5图习题15-6图15－5 由弯曲刚度EI相等的直杆形成的正方形闭合框架承受载荷如图a所示。

为利用对称性与反对称性，b、c、d、e图所示的系统，哪一种是正确的。

（A）c、d正确；（B）c正确；（C）b正确；（D）b、e正确。

正确答案是。

15－6 两个弯由刚度EI相同、半径为R的半圆环，在A、C两处铰链连接，加力方式如图所示。

关于A、B两处截面上的内力分量的绝对值，有如下四种结论，试分析哪一种是正确的。

（A）FF A=Q，0=AM，FF B=N，FRMB=；（B）FF A=Q，0=AM，2NFF B=，2FRM B=；（C）2QFF A=，0=AM，FF B=N，FRMB=；（B）2QFF A=，0=AM，2NFF B=，2FRM B=。