解直角三角形(方位角)
- 格式:ppt
- 大小:209.00 KB
- 文档页数:7


2024年解直角三角形方位角、坡度角讲课精彩教案一、教学内容1. 利用直角三角形的性质,解决实际生活中的方位角问题;2. 利用直角三角形计算坡度角,并应用于地形、建筑设计等领域。
二、教学目标1. 理解并掌握方位角与坡度角的概念及计算方法;2. 能够运用直角三角形的性质解决实际问题,如确定物体方位和计算坡度;3. 培养学生的空间想象能力和解决实际问题的能力。
三、教学难点与重点教学难点:理解方位角和坡度角的实际应用,以及计算方法的灵活运用。
教学重点:掌握直角三角形的性质,以及如何利用这些性质解决方位角和坡度角问题。
四、教具与学具准备1. 教具:直角三角形模型、地球仪、坡度计算器;2. 学具:三角板、量角器、计算器。
五、教学过程1. 实践情景引入(5分钟)利用地球仪展示不同地点的方位角,引导学生思考如何计算和确定方位角。
2. 知识讲解(15分钟)(1)回顾直角三角形的性质;(2)介绍方位角的概念及计算方法;(3)介绍坡度角的概念及计算方法。
3. 例题讲解(15分钟)(1)计算给定地点的方位角;(2)计算给定地形的坡度角。
4. 随堂练习(10分钟)(1)学生独立完成练习题,计算给定地点的方位角;(2)学生分组讨论,计算给定地形的坡度角。
六、板书设计1. 方位角的定义及计算方法;2. 坡度角的定义及计算方法;3. 例题及解答过程。
七、作业设计1. 作业题目:(1)给定一点,求该点的方位角;(2)给定一个斜面,求其坡度角。
2. 答案:(1)方位角的计算结果为:度;(2)坡度角的计算结果为:度。
八、课后反思及拓展延伸1. 反思:本节课学生对方位角和坡度角的概念理解较为顺利,但在计算过程中仍存在一些问题,如计算方法不熟练、单位换算错误等,需要在课后加强练习。
2. 拓展延伸:引导学生思考在实际生活中,还有哪些问题可以利用直角三角形的性质来解决,鼓励学生进行探索和研究。
重点和难点解析1. 实践情景引入的理解和应用;2. 知识讲解中方位角和坡度角计算方法的掌握;3. 例题讲解中解题步骤的详细解释;4. 随堂练习的设计与实施;5. 作业设计中题目难度的把握及答案的准确性;6. 课后反思与拓展延伸的有效性。



2024年解直角三角形方位角、坡度角讲课教案一、教学内容本节课我们将学习教材第十章“解直角三角形的应用”中的方位角与坡度角。
具体内容包括:理解方位角的概念,掌握利用正切值计算方位角;理解坡度角的概念,掌握利用正弦值和余弦值计算坡度角。
二、教学目标1. 理解并掌握方位角与坡度角的概念。
2. 学会使用正切、正弦和余弦值计算方位角与坡度角。
3. 能够在实际问题中运用所学的知识,解决有关方位角与坡度角的问题。
三、教学难点与重点重点:方位角与坡度角的概念及其计算方法。
难点:在实际问题中运用所学的知识,解决有关方位角与坡度角的问题。
四、教具与学具准备1. 教具:三角板、量角器、多媒体课件。
2. 学具:直角三角形模型、计算器。
五、教学过程1. 实践情景引入:通过展示实际生活中的方位角与坡度角问题,引导学生思考如何解决这些问题。
2. 知识讲解:a. 讲解方位角的概念,引导学生通过观察三角板理解方位角的含义。
b. 讲解正切值在计算方位角中的应用,通过例题进行演示。
c. 讲解坡度角的概念,引导学生通过观察直角三角形模型理解坡度角的含义。
d. 讲解正弦值和余弦值在计算坡度角中的应用,通过例题进行演示。
3. 随堂练习:让学生完成教材中的相关习题,巩固所学知识。
4. 解题方法与技巧讲解:针对学生在随堂练习中遇到的问题,进行讲解和指导。
六、板书设计1. 方位角与坡度角的概念。
2. 正切、正弦和余弦值在计算方位角与坡度角中的应用。
3. 例题解答步骤。
七、作业设计1. 作业题目:a. 计算给定直角三角形的方位角。
b. 计算给定直角三角形的坡度角。
2. 答案:见附页。
八、课后反思及拓展延伸1. 反思:本节课学生对方位角与坡度角的概念掌握情况,以及计算方法的运用。
2. 拓展延伸:引导学生思考方位角与坡度角在实际生活中的应用,如建筑设计、地形测量等。
重点和难点解析1. 教学内容的针对性及深度。
2. 教学目标的明确性与可衡量性。
3. 教学难点与重点的识别。



解直角三角形的应用-方向角问题能量储备方向角:指北或指南方向线与目标方向线所成的小于90°的水平角叫做方向角,方向角一般写成“北(或南)偏西(或东)××度”的形式。
在图2447中,目标方向线OA ,OB ,OC ,OD 的方向角分别是北偏东30°,南偏东45°,南偏西80°,北偏西60°。
另外,东南方向指的是南偏东45°,西北方向指的是北偏西45°,东北方向指的是北偏东45°,西南方向指的是南偏西45°。
通关宝典★ 基础方法点方法点:解与方向角有关的问题时,根据方向角的概念,结合图形判断相应角的度数是关键。
例1:如图2449所示,在一次军事演习中,小李从营地A 点出发,沿北偏东60°方向走了5003m 到达目标B 点,然后沿北偏西30°方向走了500 m 到达目的地C 点.(1) 求A ,C 两地之间的距离(2)确定目的地C 在营地A 的什么方向上.解:(1)∵AM ∥DN ,∴∠MAB =∠ABD =60°,∴∠CBA =180°-∠ABD -∠CBN =180°-60°-30°=90°。
∴△ABC 为直角三角形在Rt △ABC 中,AC =AB 2+BC 2= (5003)2+5002=1 000(m)。
(2) 在Rt △ABC 中,tan ∠BAC =BC AB =5005003=33, ∴∠BAC =30°,则∠MAC =∠MAB -∠BAC =60°-30°=30°答:(1)A ,C 两地之间的距离为1 000 m .(2)目的地C 在营地A 的北偏东30°方向上. 例2:如图24425所示,一艘船向东航行,上午8时到达B 处,看到有一灯塔在它的北偏东59°方向,距离它72海里的A 处;上午10时到达C 处,看到灯塔在它的正北方向.求这艘船航行的速度.(精确到1海里/时)解:在Rt △ABC 中,∠A =59°,AB =72海里,sin A =BC AB, ∴ BC =AB·sin 59°≈61.7(海里),61.7÷(10-8)≈31(海里/时).答:这艘船航行的速度约为31海里/时.蓄势待发考前攻略考真题与教材习题都是与方向角有关的航行问题,只是中考真题先要构造直角三角形.解这类题的关键是把实际问题中的有关数据转移到直角三角形中,借助解直角三角形解决问题.完胜关卡。
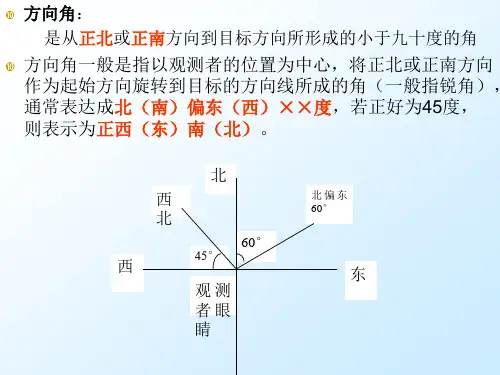


24.3.3 解直角三角形 (方位角)学习目标:1. 理解方位角的概念,并学会画方位角。
2. 会将有关方位角的实际问题转化为解直角三角形的问题并解决, 一、 复习回顾 仰角和俯角:在进行测量时,从下向上看,视线与水平线的夹角叫做仰角; 从上往下看,视线与水平线的夹角叫做俯角.二、新课(一)方位角的概念指南或指北的方向线与目标方向线构成小于900的角,叫做方位角. 如图:点A 在O 的北偏东30° 点B 在点O 的南偏西45°(西南方向)(二)利用所学概念画图1.C 岛在A 岛的北偏东60°方向,在B 岛的北偏西45°方向,则从C 岛看A,B 两岛的视角∠ACB 的度数 。
(三)例题 例1、如图,一船以20n mile/h 的速度向正东航行,在A 处测得灯塔C 在北偏东60°,继续航行1h 到达B 处,再测得灯塔C 在北偏东30°。
已知灯塔C 四周10 n mile 内有暗礁。
(1)标出方位角(2)这船继续向东航行是否安全?铅直线水平线30°45°B O A东西北南CD B A 北东(四)练习:1. 小红家(图中O 处)门前有一条东西走向的公路,测得有一水塔(图中点A 处)在她家北偏东60°的500米处,那么线段OB 的长是多少?2. 如图,海上有一座灯塔P ,在它的周围3海里内有暗礁,一艘客轮以每小时9海里的速度由西向东航行,航至A 处测得灯塔P 在它的北偏东60°方向,继续航行20分钟后,到达B 处,又测得灯塔P 在它的北偏东45°方向,问客轮不改变方向继续前进,有无触礁的危险?3.如图,小岛 A 在港口P 南偏西45°方向,距离港口81海里处,甲船从A 出发,沿AP 方向以9海里/时的速度驶向港口,乙船从港口P 出发,沿南偏东60°方向出发,以18海里/时的速度驶离港口,现两船同时出发。
第五章 空间与图形5.7 解直角三角形【基础巩固】1、勾股定理:直角三角形两直角边的平方和等于斜边的平方。
即:222c b a =+。
逆定理:如果三角形的三边长a ,b ,c 满足222c b a =+,那么这个三角形是直角三角形。
2、直角三角形的边角关系:锐角三角函数 (1). 正弦..:定义:在Rt△ABC 中,锐角∠A 的对边与斜边的比叫做∠A 的正弦,记作sinA ,即斜边的对边A A ∠=sin ;(2). 余弦:定义:在Rt△ABC 中,锐角∠A 的邻边与斜边的比叫做∠A 的余弦,记作cosA ,即斜边的邻边A A ∠=cos ;(3). 正切:定义:在Rt△ABC 中,锐角∠A 的对边与邻边的比叫做∠A 的正切..,记作tanA ,即的邻边的对边A A A ∠∠=tan(4)余切:定义:在Rt△ABC 中,锐角∠A 的邻边与对边的比叫做∠A 的余切,记作cotA ,即的对边的邻边A A A ∠∠=cot ;(5).一个锐角的正弦、余弦、正切、余切分别等于它的余角的余弦、正弦、余切、正切。
在一个直角三角形中,若∠A 为锐角,则①)90cos(sin A A ∠-︒=; )90sin(cos A A ∠-︒=解直角三角形 勾股定理锐角三角函数考查内容考查角度方向角问题楼的高度 旗杆高度 山的高度 坑的深度图 1图 3 图4 ②)90cot(tan A A ∠-︒=; )90tan(cot A A ∠-︒= (6).特殊角的锐角三角函数值3.仰角与俯角当从低处观测高处的目标时,视线与水平线 所成的锐角称为仰角.. 当从高处观测低处的目标时,视线与水平线所成 的锐角称为俯角..4. 坡角坡面与水平面的夹角叫做坡角.. (或叫做坡比..)。
用字母i 表示, 即A lhi tan ==5.方位角与方向角从某点的指北方向按顺时针转到目标方向的水平角,叫做方位角...。
如图3,OA 、OB 、OC 的方位角分别为45°、135°、225°。
解直角三角形方位角、坡度角讲课教案一、教学内容本节课我们将探讨教材第十二章“直角三角形的应用”中的方位角与坡度角。
具体内容包括:1. 理解方位角的概念,掌握其在实际情境中的应用;2. 学习坡度角的计算,了解其在工程及地理等方面的实际意义;3. 掌握运用三角函数解决实际问题时,如何确定直角三角形的各个角度和边长。
二、教学目标1. 学生能够理解并运用方位角描述物体在空间中的位置关系;2. 学生能够通过计算得出坡度角,并应用于实际情境中;3. 学生能够运用三角函数解决直角三角形相关问题。
三、教学难点与重点1. 教学难点:方位角与坡度角的实际应用,以及三角函数在解决直角三角形问题中的应用;2. 教学重点:理解方位角和坡度角的概念,掌握计算方法,并能应用于实际情境。
四、教具与学具准备1. 教具:三角板、量角器、直尺、多媒体教学设备;2. 学具:练习本、铅笔、三角板、量角器。
五、教学过程1. 实践情景引入:通过展示一座山和观察点的位置关系,引导学生思考如何描述这个关系;2. 知识讲解:(1)方位角的概念及计算方法;(2)坡度角的概念及计算方法;(3)三角函数在解决直角三角形问题中的应用;3. 例题讲解:(1)通过实际例题,讲解如何计算方位角;(2)通过实际例题,讲解如何计算坡度角;4. 随堂练习:让学生分组讨论并完成指定的练习题;5. 答疑环节:对学生在练习中遇到的问题进行解答;六、板书设计1. 方位角、坡度角的概念;2. 方位角、坡度角的计算方法;3. 三角函数在解决直角三角形问题中的应用;4. 例题解答步骤;5. 练习题。
七、作业设计1. 作业题目:(1)已知一个观察点A,以及目标点B的方位角,求目标点B 到观察点A的距离;(2)已知一个斜坡的长度和高度,求该斜坡的坡度角。
2. 答案:八、课后反思及拓展延伸1. 反思:本节课学生对方位角和坡度角的概念理解是否到位,能否将其应用于实际情境;2. 拓展延伸:引导学生思考如何将方位角和坡度角应用于其他领域,如航海、建筑等。