解直角三角形的应用(方位角)

解直角三角形及方向角的应用教课目的【知识与技术】在理解解直角三角形的含义、直角三角形五个元素之间关系的基础上, 会运用勾股定理、直角三角形的两锐角互余及锐角三角函数解直角三角形.【过程与方法】经过综合运用勾股定理、直角三角形的两锐角互余及锐角三角函数解直角三角形 , 逐渐培育学生剖析问题、解决问题的能力 .【感情、态度与价值观】在研究学习的过程中 , 培育学生合作沟通的意识, 使学生认识到数与形相结合的意义与作用 , 领会到学好数学知识的作用, 并提升学生将数学知识应用于实际的意识 , 进而体验“从实践中来 , 到实践中去”的辩证唯心主义思想, 激发学生学习数学的兴趣 . 让学生在学习过程中感觉到成功的愉悦, 产生后继学习激情 , 增强学好数学的信心 .要点难点【要点】直角三角形的解法 .【难点】灵巧运用勾股定理、直角三角形的两锐角互余及锐角三角函数解直角三角形 .、教课过程一、复习回首师: 你还记得勾股定理的内容吗?生: 记得.学生表达勾股定理的内容.师: 直角三角形的两个锐角之间有什么关系呢?生: 两锐角互余 .师: 直角三角形中 ,30 °的角所对的直角边与斜边有什么关系?生:30 °的角所对的直角边等于斜边的一半.师: 很好!二、共同研究 , 获得新知1.观点 .师: 由 sinA=, 你能获得哪些公式 ?生甲 :a=c · sinA.生乙 :c=.师: 我们还学习了余弦函数和正切函数 , 也能获得这些式子的变形 . 这些公式有一个共同的特色 , 就是式子的右端起码有一条边 , 为何会是这样的呢 ?学生思虑 .生: 由于左侧的也是边 , 依据右侧边与角的关系计算出来的应是长度.师: 对! 解三角形就是由已知的一些边或角求另一些边和角 , 我们此刻看看解直角三角形的观点 .教师板书 :在直角三角形中 , 由已知的边角关系 , 求出未知的边与角 , 叫做解直角三角形 .2.练习教师多媒体课件出示 :(1) 如图 (1) 和(2), 依据图中的数据解直角三角形 ;师: 图(1) 中是已知一角和一条直角边解直角三角形的种类 , 你如何解决这个问题呢 ?生 1: 依据 cos60°=, 获得 AB=,而后把 AC边的长和 60°角的余弦值代入 , 求出 AB边的长 , 再用勾股定理求出 BC边的长 , ∠B 的度数依据直角三角形两锐角互余即可获得 .生2: 先用直角三角形两锐角互余获得∠B为30°, 而后依据30°的角所对的直角边等于斜边的一半 , 求出 AB的值 , 再由 sin60 °=获得 BC=AB· sin60 °, 进而获得 BC边的长 .师: 你们回答得都对 ! 还有没有其余的方法了 ?生 3: 能够求出 AB后用 AB的值和∠ B 的余弦求 BC的长 .生 4: 能够在求出 AB后不用三角函数 , 用勾股定理求出 BC.师: 同学们说出这几种做法都是对的. 下边请同学们看图 (2), 并解这个直角三角形 .学生思虑 , 计算 .师: 这两个题目中已经给出了图形, 此刻我们再看几道题 .教师多媒体课件出示 :【例 1】在 Rt △ABC中, ∠ C=90°, ∠B=42°6',c=287.4,解这个直角三角形.师: 你如何解答这道题呢 ?先做什么 ?生: 先画出图形 .师: 很好 ! 此刻请同学们画出大概图形.学生绘图 .教师找一世谈谈解这个直角三角形的思路 , 而后让同学们自己做 , 最后集体订下 .解: ∠A=90°-42 °6'=47 ° 54'.由 cosB=,得a=ccosB=287.4× 0.7420 ≈213.3.由 sinB= 得b=csinB=287.4 × 0.6704 ≈192.7.教师多媒体课件出示 :【例 2】在△ ABC中 , ∠ A=55° ,b=20 cm,c=30 cm. 求△ ABC的面积 S△ABC.( 精准到 0.1 cm 2 )师: 这道题是已知了三角形的两条边和一个角, 求三角形的面积 . 要先如何 ?学生思虑 .生: 先画出图形 .师: 对, 题中没有已知图形时 , 一般都要自己画出图形 . 而后呢 ?你能给出解这道题的思路吗 ?生 1: 先计算 AB边上的高 , 以 AB为底 ,AB 边上的高为三角形的高 , 依据三角形的面积公式 , 就能计算出这个三角形的面积了 .生 2: 还能够先计算 AC边上的高 , 而后用三角形的面积公式计算这个三角形的面积 .师: 很好 ! 我们此刻议论以 AB为底时求三角形面积的方法 , 如何求 AB边上的高呢 ?教师找一世回答 , 而后集体校正 .解: 如图 , 作 AB上的高 CD.在 Rt△ACD中,CD=AC·sinA=bsinA,∴S△ABC=AB· CD=bcsinA.当∠ A=55° ,b=20 cm,c=30 cm 时 , 有S△ABC=bcsinA= × 20×30sin55 °=×20×30× 0.8192≈245.8(cm 2).教师多媒体课件出示 :【例 3】如图 , 东西两炮台 A、 B 相距 2 000 米, 同时发现入侵敌舰 C,炮台 A测得敌舰 C 在它的南偏东 40°的方向 , 炮台 B 测得敌舰 C在它的正南方 , 试求敌舰与两炮台的距离 .( 精准到 1 米 )师: 这是一个与解直角三角形相关的实质问题, 你能将它转变为数学模型吗?学生思虑后回答 : 会.师: 这相当于已知了哪些条件, 让你求什么量 ?生: 已知直角三角形的一个锐角和一条直角边, 求它的斜边和另向来角边.师: 你回答得很好 ! 此刻请同学们计算一下.学生计算 , 教师巡视指导 , 最后集体校正 .解: 在 Rt△ABC中 ,∵∠ CAB=90°- ∠ DAC=50°,=tan ∠ CAB,∴BC=AB·tan ∠CAB=2 000×tan50 °≈ 2 384( 米)又∵ =cos50°,∴AC==≈3 111( 米).答: 敌舰与 A、B 两炮台的距离分别约为 3 111 米和 2 384 米.三、练习新知师: 此刻请同学们看课本第125 页练习 1 的第 (1) 、 (2) 题.教师找两生各板演 1 题, 其余同学在下边做 , 而后集体校正 .解:(1)∠A=90°-80 °=10° ,AB=≈≈ 172.81,AC=≈≈ 170.16,(2)BC===≈ 7.42.cosA===0.375,∠A≈67.976 °≈ 67°58'32 ″,∠B=90°- ∠A=22°1'28 ″.教师找一世板演课本第125 页练习的第 3 题, 其余同学在下边做 , 而后集体订正 .解:过点 A 向 DC作垂线 , 与 DC交于一点 E.AE=ADsin43°=6×sin43 °≈6× 0.682=4.092.S=(AB+DC)×AE=(4+8) × 4.092≈24.55.答: 梯形的面积为 24.55.四、稳固提升师: 同学们 , 经过方才的学习 , 相信大家都掌握了必定的解直角三角形及其应用题的方法 , 此刻我出几道习题来检测下大家学得怎么样 !教师多媒体课件出示习题:1.在△ ABC中, ∠C=90°, 以下各式中不正确的选项是 ( ) A.b=a· tanB B.a=b ·cosAC.c=D.c=【答案】 B2. 在 Rt△ABC中, ∠C=90°,a=35,b=28, 则 tanA= ,tanB=.【答案】3. 在 Rt△ABC中, ∠C=90°,c=10,b=5, 则∠ A= ,S △ABC=.【答案】 30°4.已知在 Rt △ABC中 , ∠ C=90° ,a=104,b=20.49, 求∠ A 和∠ B.( 可利用计算器进行运算 , 精准到 1° )【答案】∠ A=79°, ∠B=11°5.如图 , 在 Rt△ ABC中,BC=7.85,AB=11.40, 解这个直角三角形 .( 边长保存三个有效数字 , 角度精准到 1°)【答案】 AC=8.27,∠ A=44° , ∠ B=46°五、讲堂小结师: 本节课 , 我们学习了什么内容 ?学生回答 .师: 你还有什么不懂的地方吗?学生发问 , 教师解答 .教课反省本节课在教课过程中 , 能灵巧办理教材 , 敢于松手让学生经过自主学习、合作研究 , 达到理解并掌握知识的目的 , 并能运用知识解决问题 . 在本章开头 , 我率领学生复习了与解直角三角形相关的知识点 , 使学生在解决问题时能想到并能娴熟运用 . 在解有特别角的三角形时有不只一种解法 , 我鼓舞学生勇于讲话 , 给了他们展现自我的时机 , 锻炼他们表达自己想法的能力 , 而且加强了他们的自信心 .。

1.如下图，某船以每小时36海里的速度向正东方向航行，在点A 测得某岛C 在北偏东60°方向上，航行半小时后到达点B 测得该岛在北偏东30°方向上，已知该岛周围16海里内有暗礁。

（1）说明点B 是否在暗礁区域内；（2）若继续向东航行有无触礁的危险？请说明理由。

2.如图，海岛A 四周20海里周围内为暗礁区，一艘货轮由东向西航行，在B 处见岛A 在北偏西60˚，航行24海里到C ，见岛A 在北偏西15˚，货轮继续向西航行，有无触礁的危险3.如图所示，A 、B 两城市相距100km ．现计划在这两座城市间修筑一条高速公路（即线段AB ），经测量，森林保护中心P 在A 城市的北偏东30°和B 城市的北偏西45°的方向上．已知森林保护区的范围在以P 点为圆心，50km 为半径的圆形区域内．请问计划修筑的这条高速公路会不会穿越保护区．为什么？（参考数据：3 1.7322 1.414≈，≈）4.为打击索马里海盗，保护各国商船的顺利通行，我海军某部奉命前往该海域执行护航任务．某天我护航舰正在某小岛A 北偏西45°并距该岛20海里的B 处待命．位于该岛正西方向C 处的某外国商船遭到海盗袭击，船长发现在其北偏东60°的方向有我军护航舰（如图所示），便发出紧急求救信号．我护航舰接警后，立即沿BC 航线以每小时60海里的速度前去救援．问我护航舰需多少分钟可以到达该商船所在的位置C 处？（结果精确到个位）5.如图，某天然气公司的主输气管道从A 市的东偏北30°方向直线延伸，测绘员在A 处测得要安装天然气的M 小区在A 市东偏北60°方向，测绘员沿主输气管道步行2000米到达C 处，测得小区M 位于C 的北偏西60°方向，请你在主输气管道上寻找支管道连接点N ，使到该小区铺设的管道最短，并求AN 的长.6.如图，A 城气象台测得台风中心在A 城的正西方300千米处，以每小时10千米的速度向北偏东60º的BF 方向移动，距台风中心200千米的范围内是受这次台风影响的区域。

在线分享文档用解直角三角形解方位角的应用一、教学目标(一)知识与技能巩固直角三角形中锐角的三角函数，学会解关于方位角的问题．(二)过程与方法逐步培养学生分析问题解决问题的能力，进一步渗透数形结合的数学思想和方法．(三)情感态度与价值观培养学生用数学的意识；渗透数学来源于实践又反过来作用于实践的辩证唯物主义观点．二、重、难点重点：能熟练运用有关三角函数知识．难点：解决实际问题．三、教学过程(一)明确目标讲评上课节课后作业(二)重点、难点的学习与目标完成过程教师出示例题．例1 如图，在山坡上种树，要求株距(相邻两树间的水平距离)是5.5m，测得斜坡的倾斜角是24°，求斜坡上相邻两树的坡面距离是多少(精确到0.1m)．分析：1．例题中出现许多术语——株距，倾斜角，这些概念学生未接触过，比较生疏，而株距概念又是学生易记错之处，因此教师最好准备教具：用木板钉成一斜坡，再在斜坡上钉几个铁钉，利用这种直观教具更容易说明术语，符合学生的思维特点．2．引导学生将实际问题转化为数学问题画出图形(上图(2))．已知：Rt△ABC中，∠C=90°，AC=5.5，∠A=24°，求AB．3．学生运用解直角三角形知识完全可以独立解决例1．教师可请一名同学上黑在线分享文档板做，其余同学在练习本上做，教师巡视．答：斜坡上相邻两树间的坡面距离约是6.0米．教师引导学生评价黑板上的解题过程，做到全体学生都掌握．例2 如图6-30，沿AC方向开山修渠，为了加快施工速度，要从小山的另一边同时施工，从AC上的一点B取∠ABD=140°，BD=52cm，∠D=50°，那么开挖点E离D多远(精确到0.1m)，正好能使A、C、E成一条直线？这是实际施工中经常遇到的问题．应首先引导学生将实际问题转化为数学问题．由题目的已知条件，∠D=50°，∠ABD=140°，BD=520米，求DE为多少时，A、C、E在一条直线上。

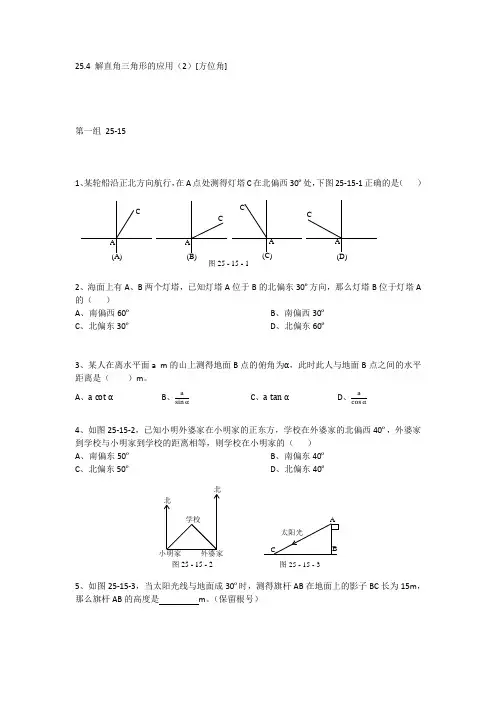
25.4 解直角三角形的应用（2）[方位角]第一组 25-151、某轮船沿正北方向航行，在A 点处测得灯塔C 在北偏西30º处，下图25-15-1正确的是（ ）2、海面上有A 、B 两个灯塔，已知灯塔A 位于B 的北偏东30º方向，那么灯塔B 位于灯塔A 的（ ）A 、南偏西60ºB 、南偏西30ºC 、北偏东30ºD 、北偏东60º3、某人在离水平面a m 的山上测得地面B 点的俯角为α，此时此人与地面B 点之间的水平距离是（ ）m 。

A 、a cot α B 、a sin αC 、a tan αD 、acos α4、如图25-15-2，已知小明外婆家在小明家的正东方，学校在外婆家的北偏西40º，外婆家到学校与小明家到学校的距离相等，则学校在小明家的（ ） A 、南偏东50º B 、南偏东40º C 、北偏东50º D 、北偏东40º5、如图25-15-3，当太阳光线与地面成30º时，测得旗杆AB 在地面上的影子BC 长为15m ，那么旗杆AB 的高度是 m 。

（保留根号）图 25 - 15 - 1(D)A CA C CA CA 图 25 - 15 - 2小明家学校北北图 25 - 15 - 3BA太阳光C6、某人从A 点出发，向北偏东45º方向走到B 点，再从B 点出发，向南偏西15º方向走到C 点，那么∠ABC= 。

7、如图25-15-4，点B 在点A 北偏西30º方向，且AB=5km ，点C 在点B 北偏东60º方向，且BC=12km ，则A 到C 的距离是 。

8、如图25-15-5，一轮船以每小时20海里的速度沿正东方向航行，上午8时，该船在A 处测得某灯塔位于它的北偏东30º的B 处，上午9时行至C 处，测得灯塔恰好在它的正北方向，此时它与灯塔的距离是 海里。

:i h l=hlα基础知识2解直角三角形的应用举例1.仰角与俯角：仰角：视线在水平线上方的角；俯角：视线在水平线下方的角。

2.坡度与坡角：坡面的铅直高度h 和水平宽度l 的比叫做坡度(坡比)。

用字母i 表示，即hi l=。

坡度一般写成1:m 的形式，如1:5i =等. 把坡面与水平面的夹角记作α(叫做坡角)，那么tan hi lα== 3.方位角：指北或指南方向线与目标方向线所成的小于90°的水平角，叫做方位角.如图,OA 、OB 、OC 、OD 的方向角分别是：北偏东30°（东北方向），南偏东45°（东南方向），南偏西60°（西南方向），北偏西60°（西北方向）.【题型1】仰角与俯角如图，两幢建筑物AB 和CD ，AB ⊥BD ，CD ⊥BD ，AB ＝15m ，CD ＝20m ，AB 和CD 之间有一观景池，小南在A 点测得池中喷泉处E 点的俯角为42°，在C 点测得E 点的俯角为45°（点B 、E 、D 在同一直线上），求两幢建筑物之间的距离BD （结果精确到0.1m ）.（参考数据：sin 42°≈0.67，cos 42°≈0.74，tan 42°≈0.90）【变式训练】1.如图,宁宁在家里楼顶上的点A处，测量建在与自家楼房同一水平线上相邻的电梯楼的高，在点A处看电梯楼顶部点B处的仰角为60°，在点A处看这栋电梯楼底部点C处的俯角为45°，两栋楼之间的距离为30m，则电梯楼的高BC为多少米（精确到0.1）.2.如图，大楼AB右侧有一障碍物，在障碍物的旁边有一幢小楼DE，在小楼的顶端D处测得障碍物边缘点C的俯角为30°，测得大楼顶端A的仰角为45°（点B，C，E在同一水平直线上），已知AB=80m，DE=10m，求障碍物B，C两点间的距离（结果精确到0.1m）.（参考数据：≈1.414，≈1.732）3.如图，热气球的探测器显示，从热气球A看一栋大楼顶部B的俯角为30°，看这栋大楼底部C的俯角为60°，热气球A的高度为240米，求这栋大楼的高度．4.如图，曦曦在M处用高1米(DM＝1米)的测角仪测得旗杆AB的顶端B的仰角为30°，再向旗杆方向前进10米到F处，又测得旗杆顶端B的仰角为60°，请求出旗杆AB的高度．【题型2】坡度与坡角如图，某水库堤坝横断面迎水坡AB的坡比是1，堤坝高BC=50m，则应水坡面AB的长度是多少？【变式训练】1.如图，在坡度为1∶2的山坡上种树，要求株距(相邻两树间的水平距离)是6米，斜坡上相邻两树间的坡面距离是多少米？2.如图，为了缓解交通拥堵，方便行人，在某街道计划修建一座横断面为梯形ABCD的过街天桥，若天桥斜坡AB的坡角∠BAD为35°，斜坡CD的坡度为i＝1∶1.2(垂直高度CE与水平宽度DE的比)，上底BC＝10 m，天桥高度CE＝5 m，求天桥下底AD的长度．(结果精确到0.1 m，参考数据：sin35°≈ 0.57，cos35°≈ 0.82，tan35°≈ 0.70)3.如图，一楼房AB后有一假山，其坡度为i＝1∶3，山坡坡面上E点处有一休息亭，测得假山坡脚C与楼房水平距离BC＝25米，与亭子距离CE＝20米，小丽从楼房顶测得E点的俯角为45°，求楼房AB的高．(注：坡度i是指坡面的铅直高度与水平宽度的比).4.如图，曦曦在山坡坡脚A 处测得电视塔尖点C 的仰角为60° ，沿山坡向上走到P 处再测得点C 的仰角为45° ，已知OA=100米，山坡坡度为i=1:2， 且O 、A 、B 在同一条直线上。

【浙教版】2022年九年级（上）期末复习培优提分专项训练解直角三角形的应用（方位角问题）1．（2022·浙江宁波·一模）如图，某渔船沿正东方向以10海里／小时的速度航行，在A处测得岛C在北偏东60°方向，1小时后渔船航行到B处，测得岛C在北偏东30°方向，已知该岛周围9海里内有暗礁．参考数据：√3≈1.732，sin75°≈0.966，cos75°≈0.259．(1)B处离岛C有多远？如果渔船继续向东航行，有无触礁危险？(2)如果渔船在B处改为向东偏南15°方向航行，有无触礁危险？2．（2022·浙江宁波·九年级专题练习）我国海域辽阔，渔业资源丰富，如图，现有渔船以18√2km/ℎ的速度在海面上沿正东方向航行，当行至A处时，发现它的东南方向有一灯塔B，船续向东航行30min后达到C处，发现灯塔B在它的南偏东15°方向．(1)求此时渔船与灯塔B的距离．(2)若渔船继续向东行驶，还要行驶多少千米与B的距离达到最小值．（参考数据：sin75°≈0.97，cos75°≈0.26，tan75°≈3.73）3．（2022·浙江宁波·一模）如图，C岛在A岛的北偏东45°方向，在B岛的北偏西25°方向．(1)直接写出∠ACB的度数是；(2)测量发现∠BAC=20°，A岛与C岛之间的距离AC=20海里，求A岛与B岛之间的距离．（结果精确到0.1海里）（参考数据：sin20°≈0.34，cos20°≈0.94，tan20°≈0.36）4．（2021·浙江丽水·一模）如图，某海岸边有B，C两个码头，C码头位于B码头的正东方向，距离B码头60海里．甲、乙两船同时从A岛出发，甲船向位于A岛正北方向的B码头航行，乙船向位于A岛北偏东30°方向的C码头航行，当甲船到达距离B码头45海里的E 处时，乙船位于甲船北偏东60°方向的D处，求此时乙船与C码头之间的距离．（结果保留根号）5．（2022·浙江·一模）小明在A点测得C点在A点的北偏西75°方向，并由A点向南偏西45°方向行走到达B点测得C点在B点的北偏西45°方向，继续向正西方向行走2km后到达D 点，测得C点在D点的北偏东22.5°方向，求A，C两点之间的距离．（结果保留0.1km．参数数据√3≈1.732）6．（2022·浙江金华·一模）某海域有A，B两个岛屿，B岛在A岛北偏西30°方向上，距A岛120海里．有一艘船从A岛出发，沿东北方向行驶一段距离后，到达位于B岛南偏东75°方向的C处．(1)求∠BCA的度数．(2)求BC的长．7．（2022·浙江宁波·九年级期末）如图，某渔船向正东方向以14海里/时的速度航行，在A处测得小岛C在北偏东70∘方向，2小时后渔船到达B处，测得小岛C在北偏东45∘方向，已知该岛周围20海里范围内有暗礁．（参考数据：sin70∘≈0.94,cos70∘≈0.34,tan70∘≈2.75,√2≈1.41）(1)求B处距离小岛C的距离（精确到0.1海里）；(2)为安全起见，渔船在B处向东偏南转了25∘继续航行，通过计算说明船是否安全？8．（2021·浙江·杭州外国语学校九年级阶段练习）阅读下列材料，并解决问题．如图（1），在锐角△ABC中，∠A，∠B，∠C的对边分别是a，b，c，过点A作AD∠BC于点D，则sinB=ADc ，sinC=ADb，即AD＝c sin B，AD＝b sin C．于是c sin B＝b sin C，即bsinB=csinC．同理有：csinC =asinA，asinA=bsinB，所以asinA=bsinB=csinC．即在一个三角形中，各边和它所对角的正弦的比相等．在锐角三角形中，若已知三个元素（至少有一条边），运用上述结论就可以求出其余三个未知元素．（1）如图（2），一货轮在B处测得灯塔A在货轮的北偏东15°的方向上，随后货轮以80海里/时的速度向正东方向航行，半小时后到达C处，此时又测得灯塔A在货轮的北偏西30°的方向上，求此时货船距灯塔A的距离AC．（2）在（1）的条件下，试求75°的正弦值．（结果保留根号）9．（2020·浙江衢州·九年级期末）某社会实践活动小组实地测量河两岸互相平行的一段河的宽度，在河的南岸边点A处，测得河的北岸边点B在其北偏东45°方向，然后向西走50m 到达C点，测得点B在点C的北偏东60°方向，如图．（1）求∠CBA的度数；（2）求这段河的宽度．（结果精确到1m）10．（2022·重庆·四川外国语大学附属外国语学校九年级期中）期中测试临近学生都在紧张的复习中，小甘和小西相约周末去图书馆复习，如图，小甘从家A地沿着正东方向走900m 到小西家B地，经测量图书馆C地在B地的北偏东15°，C地在A地的东北方向．(1)求AC的距离：(2)两人准备从B地出发，实然接到疾控中心通知，一名确诊的新冠阳性患者昨天经过了C 地，并沿着C地南偏东22°走了1800m到达D地，根据相关要求，凡是确诊者途径之处800m 区域以内都会划为管控区，问：小西家会被划为管控区吗？请说明理由（参考数据：√3≈1.73,√2≈1.41,√6≈2.45,sin37°≈0.6,cos37°≈0.8,tan37°≈0.75）．11．（2021·河南·辉县市太行中学九年级期中）如图，一位自行车爱好者沿宿鸭湖湖边正东方向笔直的公路BC骑行，在B地测得湖中小岛上某建筑物A在北偏东45°方向，行驶12min 后到达C地，测得建筑物A在北偏西60°方向，如果此自行车爱好者的速度为60km/h，求建筑物A到公路BC的距离．（结果保留根号）【分母有理化：√3+1=√3−1(√3+1）)(√3-−1)=√3−12】12．（2022·上海市民办新复兴初级中学九年级期中）如图，一艘海岸巡逻快艇在基地A的正东方向，且距A地13海里的B处巡逻．突然接到基地A命令，要该快艇前往C岛，接送一名病人到基地A的医院救治．已知C岛在基地A的南偏东α的方向，且在B处南偏东β的方向，巡逻快艇从B处出发，平均每小时行驶30海里，需要多少时间才能把病人送到基地A的医院？（参考数据：tanα=158，sinβ=45）13．（2022·山东青岛·九年级期中）九年级二班学生到某劳动教育实践基地开展实践活动，当天，他们先从基地门口A处向正北方向走了220米，到达菜园B处锄草，再从B处沿正西方向走了200米，到达果园C处采摘水果，再向南偏东37°方向走了200米，到达手工坊D处进行手工制作，最后从D处回到门口A处．(1)求从手工坊D处回到门口A处的距离．(2)求从手工坊D处回到门口A处的方位角．[参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75]14．（2022·重庆一中九年级阶段练习）公园大门A的正东方向原本有一条通往湖心小岛B的景观步道AB，但为了让市民朋友多角度欣赏公园景色，市政府决定新修一条景观步道通往湖心小岛B，新步道从A出发通向C地，C位于A的北偏西45°方向，AC=800米，再从C 地到达湖心小岛B，其中C位于B的北偏西60°方向，甲工程队以每天60米的速度进行单独施工，2天后，为了加快工程进度，乙工程队以每天90米的速度加入项目建设，直到两队起完成景观步道的修建．（参考数据：√2≈1.4）(1)求A、B两地的距离（结果保留根号）；(2)新的景观步道能否在15天内完成？请说明理由．15．（2022·山东·济南市大学城实验学校九年级阶段练习）如图，三角形花园ABC紧邻湖泊，四边形ABDE是沿湖泊修建的人行步道．经测量，点C在点A的正东方向，AC=200米．点E在点A的正北方向．点B，D在点C的正北方向，BD=100米．点B在点A的北偏东30°，点D在点E的北偏东45°．(1)求步道DE的长度（精确到个位）；(2)点D处有直饮水，小红从A出发沿人行步道去取水，可以经过点B到达点D，也可以经过点E到达点D．请计算说明他走哪一条路较近？（参考数据：√2≈1.4，√3≈1.7）16．（2022·上海·九年级专题练习）如图，在东西方向的海岸线l上有长为300米的码头AB，在码头的最西端A处测得轮船M在它的北偏东45°方向上；同一时刻，在A点正东方向距离100米的C处测得轮船M在北偏东22°方向上．（参考数据：sin22°≈0.375，cos22°≈0.927，tan22°≈0.404，√3≈1.732．）(1)求轮船M到海岸线l的距离；（结果精确到0.01米）(2)如果轮船M沿着南偏东30°的方向航行，那么该轮船能否行至码头AB靠岸？请说明理由．17．（2022·上海·九年级专题练习）如图，在航线l的两侧分别有两个灯塔A和B，灯塔A到航线l的距离为AC=3千米，灯塔B到航线l的距离为BD=4千米，灯塔B位于灯塔A南偏东60°方向．现有一艘轮船从位于灯塔B北偏西53°方向的N（在航线l上）处，正沿该航线自东向西航行，10分钟后该轮船行至灯塔A正南方向的点C（在航线l上）处．（参考数据：√3≈1.73，sin53°≈0.80，cos53°≈0.60，tan53°≈1.33）(1)求两个灯塔A和B之间的距离；(2)求该轮船航行的速度（结果精确到0.1千米/小时）．18．（2022·重庆八中九年级阶段练习）如图，在竖直的海岸线上有长为68米的码头AB，现有一艘货船在点P处，从码头A处测得货船在A的东南方向，若沿海岸线向南走30米后到达点C，在C处测得货船在C的南偏东75°方向．（参考数据：√2≈1.41，√3≈1.73，√6≈2.45）(1)求货船到A的距离（结果精确到1米）；(2)若货船从点P出发，沿着南偏西60°的方向行驶，请问该货船能否行驶到码头所在的线段AB上？请说明理由．19．（2022·四川·仁寿县黑龙滩镇光相九年制学校九年级期末）小明周未与父母一起到眉山湿地公园进行数学实践活动，在A处看到B，C处各有一棵被湖水隔开的银杏树.他在A处测得B在西北方向，C在北偏东30°方向.他从A处走了20米到达B处，又在B处测得C在北偏东60°方向．(1)求∠C的度数；(2)求两棵银杏树B，C之间的距离．（结果保留根号）20．（2022·广东·广州市越秀区育才实验学校二模）如图，我国一艘海监执法船在南海海域进行常态化巡航，在A处测得北偏东30°方向距离为40海里的B处有一艘可疑船只正在向正东方向航行，我海监执法船便迅速沿北偏东75°方向前往监视巡查，经过一段时间在C处成功拦截可疑船只．求我海监执法船前往监视巡查的过程中行驶的路程（即AC长）？（结果精确到0.1海里，√3≈1.732，√2≈1.414，√6≈2.449）21．（2021·山东·泰安市泰山区大津口中学九年级阶段练习）如图，在一笔直的海岸线l上有AB两个观测站，A在B的正东方向，AB=2（单位：km）．有一艘小船在点P处，从A测得小船在北偏西60°的方向，从B测得小船在北偏东45°的方向．(1)求点P到海岸线l的距离；(2)小船从点P处沿射线AP的方向航行一段时间后，到点C处，此时，从B测得小船在北偏西15°的方向．求点C与点B之间的距离．（上述两小题的结果都保留根号）22．（2022·湖南湘潭·八年级期末）如图，一艘渔船以30海里/h的速度由西向东追赶鱼群，在A处测得小岛C在船的北偏东60°方向；40min后，渔船行至B处，此时测得小岛C在船的北偏东30°方向．已知以小岛C为中心，周围10海里以内有暗礁，问这艘渔船继续向东追赶鱼群是否有触礁的危险？23．（2022·黑龙江·哈尔滨市风华中学校九年级阶段练习）如图，海中有一个小岛A，它周围8n mile 内有暗礁. 渔船跟踪鱼群由西向东航行，在B点测得小岛A在北偏东60∘方向上，航行12n mile 到达D点，这时测得小岛A在北偏东30∘方向上．如果渔船不改变航线继续向东航行，有没有触礁的危险？24．（2022·黑龙江·大庆市祥阁学校九年级期中）为了维护我国海域安全，某巡逻艇从码头A 出发向东航行40海里后到达B处，再从B处沿北偏东30°方向行驶40海里到达C处，然后沿北偏西60°方向航行到D处，发现码头A在正南方向．求此时巡逻艇与码头A的距离．(结果保留根号）25．（2022·四川资阳·中考真题）小明学了《解直角三角形》内容后，对一条东西走向的隧道AB进行实地测量．如图所示，他在地面上点C处测得隧道一端点A在他的北偏东15°方向上，他沿西北方向前进100√3米后到达点D，此时测得点A在他的东北方向上，端点B在他的北偏西60°方向上，（点A、B、C、D在同一平面内）(1)求点D与点A的距离；(2)求隧道AB的长度．（结果保留根号）26．（2022·重庆市江津中学校八年级阶段练习）某海域有一小岛P，在以P为圆心，半径r 为10(3+√3)海里的圆形海域内有暗礁．一海监船自西向东航行，它在A处测得小岛P位于北偏东60°的方向上，当海监船行驶20√5海里后到达B处，此时观测小岛P位于B处北偏东45°方向上．(1)求A、P之间的距离AP；(2)若海监船由B处继续向东航行是否有触礁危险？请说明理由．27．（2022·重庆市第三十七中学校九年级阶段练习）海洋安全预警系统为海洋安全管理起到了巨大作用，某天海洋监控中心收到信息，在A的北偏西60°方向的120海里的C处，疑似有海盗船在沿CB方向行驶，C在B的北偏西30°方向上，监控中心向A正西方向的B处海警船发出指令，海警船立即从B出发沿BC方向行驶，在距离A为60√2海里的D处拦截到该可疑船只．(1)求点A到直线CB的距离；(2)若海警船的速度是30海里/小时，那么海警船能否在1小时内拦截到可疑船只？请说明理由．（结果保留一位小数，参考数据：√3≈1.73）28．（2021·河南·油田十中九年级阶段练习）如图，是学生小金家附近的一块三角形绿化区的示意图；为增强体质，他每天早晨都沿着绿化区周边小路AB，BC，CA跑步（小路的宽度不计），观测得点B在点A的南偏东30°方向上，点C在点A的南偏东60°的方向上，点B 在点C的北偏西75°方向上，AC间距离为400米．小金沿三角形绿化区的周边小路跑一圈共跑了多少米？（结果精确到1米，参考数据：√2≈1.4，√3≈1.7）29．（2022·贵州安顺·中考真题）随着我国科学技术的不断发展，5G移动通信技术日趋完善．某市政府为了实现5G网络全覆盖，2021~2025年拟建设5G基站3000个，如图，在斜坡CB上有一建成的5G 基站塔AB ，小明在坡脚C 处测得塔顶A 的仰角为45°，然后他沿坡面CB 行走了50米到达D 处，D 处离地平面的距离为30米且在D 处测得塔顶A 的仰角53°．（点A 、B 、C 、D 、E 均在同一平面内，CE 为地平线）（参考数据：sin53°≈45，cos53°≈35，tan53°≈43）(1)求坡面CB 的坡度；(2)求基站塔AB 的高．30．（2022·辽宁丹东·中考真题）如图，我国某海域有A ，B ，C 三个港口，B 港口在C 港口正西方向33.2nmile （nmile 是单位“海里”的符号）处，A 港口在B 港口北偏西50°方向且距离B 港口40nmile 处，在A 港口北偏东53°方向且位于C 港口正北方向的点D 处有一艘货船，求货船与A 港口之间的距离．（参考数据：sin50°≈0.77，cos50°≈0.64，tan50°≈1.19，sin53°≈0.80，cos53°≈0.60，tan53°≈1.33．）。

二、解直角三角形的运用--仰角与俯角知识点1 解直角三角形1. 解直角三角形的定义在直角三角形中，由已知元素求未知元素的过程就是解直角三角形． 2.解直角三角形要用到的关系 （1）锐角直角的关系：∠A+∠B=90° （1）三边之间的关系：a 2+b 2=c 2（3）边角之间的关系：c a A ==斜边对边sin ，c b A ==斜边邻边cos ，baA ==邻边对边tan （a ，b ，c 分别是∠A 、∠B 、∠C 的对边） 知识点2 方向角方向角的概念：是指采用某坐标轴方向作为标准方向所确定的方位角。

一．选择题（共7小题）1．如图为东西流向且河岸平行的一段河道，点A ，B 分别为两岸上一点，且点B 在点A 正北方向，由点A 向正东方向走a 米到达点C ，此时测得点B 在点C 的北偏西55°方向上，则河宽AB 的长为（ ）方向角知识导航A．a tan55°米B．米C．米D．米【解答】解：连接AB，BC，由题意得，∠BAC＝90°，∠ABC＝55°，AC＝a米，∴tan∠ABC＝tan55°＝，∴AB＝＝，故选：D．2．如图，一艘海伦位于灯塔P的南偏东37°方向，距离灯塔40海里的A处，它沿正北方向航行一段时间后，到达位于灯塔的正东方向上的B处，这时，B处与灯塔P的距离PB 的长可以表示为（）A．40海里B．40sin37°海里C．40cos37°海里D．40tan37°海里【解答】解：∵一艘海轮位于灯塔P的南偏东37°方向，∴∠BAP＝37°，∵AP＝40海里，∴BP＝AP•sin37°＝40sin37°海里；故选：B．3．如图，一艘轮船在A处测的灯塔C在北偏西15°的方向上，该轮船又从A处向正东方向行驶20海里到达B处，测的灯塔C在北偏西60°的方向上，则轮船在B处时与灯塔C之间的距离（即BC的长）为（）A．40海里B．（20+10）海里C．40海里D．（10+10）海里【解答】解：过A作AD⊥BC于D，如图所示：在Rt△ABD中，∠ABD＝90°﹣60°＝30°，AB＝20海里，∴AD＝AB＝10（海里），BD＝AD＝AB＝10（海里），∵∠ABC＝90°﹣60°＝30°，∠BAC＝90°+15°＝105°，∴∠C＝180°﹣105°﹣30°＝45°，∴△ACD是等腰直角三角形，∴CD＝AD＝10（海里），∴BC＝BD+CD＝（10+10）海里，故选：D．4．如图，一般客轮从小岛A沿东北方向航行，同时一艘补给船从小岛A正东方向相距（100+100）海里的港口B出发，沿北偏西60°方向航行，与客轮同时到达C处给客轮进行补给，则客轮与补给船的速度之比为（）A．：2 B．：1 C．：2 D．：1【解答】解：过C作CD⊥AB于D，设AD＝x，由题意得∠CAD＝45°，∠NBC＝60°，在Rt△ACD中，∠ACD＝90°﹣45°＝45°，∴∠ACD＝∠CAD，∴CD＝AD＝x，∴AC＝＝x，在Rt△BCD中，∠CBD＝90°﹣60°＝30°，∴BC＝2CD＝2x，∴BD＝＝x，∵AB＝100+100，∴AD+BD＝x+x＝100+100，∴（1+）x＝100（1+），∴x＝100，即AD＝100海里，∴AC＝100海里，BC＝200海里，∵时间一定时速度与路程成正比，∴客轮与补给船的速度之比为100：200＝：2，故选：A．5．如图，一渔船以32海里/时的速度向正北航行，在A处看到灯塔S在渔船的北偏东30°，半小时后航行到B处看到灯塔S在船的北偏东60°，若渔船继续向正北航行到C处时，此时渔船在灯塔S的正西方向，此时灯塔S与渔船的距离（）A．16海里B．18海里C．8海里D．8海里【解答】解：由题意得，AB＝32×＝16（海里），∠ACS＝90°，∵∠A＝30°，∠CBS＝60°，∴∠ASB＝∠CBS﹣∠A＝30°，∴∠ASB＝∠A，∴BS＝AB＝16（海里），在Rt△CBS中，sin∠CBS＝，∴CS＝BS•sin∠CBS＝16×＝8（海里），故选：D．6．如图，有一轮船在A处测得南偏东30°方向上有一小岛P，轮船沿正南方向航行至B处，测得小岛P在南偏东45°方向上，按原方向再航行10海里至C处，测得小岛P在正东方向上，则A，B之间的距离是（）A．10海里B．（10﹣10）海里C．（10﹣10）海里D．10海里【解答】解：由题意得：∠CAP＝30°，∠CBP＝45°，BC＝10海里，在Rt△APC中，∵∠CAP＝30°，∴AC＝＝＝10（海里），∴AB＝AC﹣BC＝（10﹣10）海里．故选：C．7．如图，在A处测得点P在北偏东60°方向上，在B处测得点P在北偏东30°方向上，若AP＝6千米，则A，B两点的距离为（）千米．A．4 B．4C．2 D．6【解答】解：由题意知，∠P AB＝30°，∠PBC＝60°，∴∠APB＝∠PBC﹣∠P AB＝60°﹣30°＝30°，∴∠P AB＝∠APB，∴AB＝PB，在Rt△P AC中，∵AP＝6千米，∴PC＝P A＝3千米，在Rt△PBC中，∵sin∠PBC＝，∴PB＝＝＝6千米．故选：D．二．解答题（共8小题）8．一辆小汽车在某城市道路上自西向东行驶，某“玩转数学”活动小组在距路边20米的点C处放置了“检测仪器”，测得该车从北偏西60°方向的点A行驶到东北方向的点B，所用时间为6秒．（1）求AB的长；（2）求该车的速度约为多少米/秒？（精确到0.1，参考数据：≈1.414，≈1.732）【解答】解：（1）由题意可知，CD＝20m，∠ACD＝60°，∠BCD＝45°，在Rt△ACD中，∠ACD＝60°，CD＝20m，∴AD＝tan∠ACD•CD＝20（m），在Rt△BCD中，∠BCD＝45°，CD＝20m，∴BD＝CD＝20m，∴AB＝AD+BD＝（20+20）m，答：AB的长度为（20+20）m；（2）该车的速度为（20+20）÷6≈9.1（米/秒），答：该车的速度约为9.1米/秒．9．如图，某海岸线M的方向为北偏东75°，甲、乙两船同时出发向C处海岛运送物资．甲船从港口A处沿北偏东45°方向航行，乙船从港口B处沿北偏东30°方向航行，其中乙船的平均速度为v．若两船同时到达C处海岛，求甲船的平均速度．（结果用v表示．参考数据：≈1.4，≈1.7）【解答】解：过点C作CD⊥AM，垂足为D，由题意得，∠CAD＝75°﹣45°＝30°，∠CBD＝75°﹣30°＝45°，设CD＝a，则BD＝a，BC＝a，AC＝2CD＝2a，∵两船同时到达C处海岛，∴t甲＝t乙，即＝，∴＝，∴V甲＝＝v≈1.4v．10．小张早起在一条东西走向的笔直马路上晨跑，他在A处时，D处学校和E处图书馆都在他的东北方向，当小张沿正东方向跑了600m到达B处时，E处图书馆在他的北偏东15°方向，然后他由B处继续向正东方向跑600m到达C处，此时D处学校在他的北偏西63.4°方向，求D处学校和E处图书馆之间的距离．（结果保留整数）（参考数据：sin63.4°≈0.9，cos63.4°≈0.4，tan63.4°≈2.0，≈1.4，≈1.7，≈2.4）【解答】解：过D作DM⊥AC于M，设MD＝x，在Rt△MAD中，∠MAD＝45°，∴△ADM是等腰直角三角形，∴AM＝MD＝x，∴AD＝x，在Rt△MCD中，∠MDC＝63.4°，∴MC≈2MD＝2x，∵AC＝600+600＝1200，∴x+2x＝1200，解得：x＝400，∴MD＝400m，∴AD＝MD＝400，过B作BN⊥AE于N，∵∠EAB＝45°，∠EBC＝75°，∴∠E＝30°，在Rt△ABN中，∠NAB＝45°，AB＝600，∴BN＝AN＝AB＝300，∴DN＝AD﹣AN＝400﹣300＝100，在Rt△NBE中，∠E＝30°，∴NE＝BN＝×300＝300，∴DE＝NE﹣DN＝300﹣100≈580（m），即临D处学校和E处图书馆之间的距离是580m．11．如图，线段EF与MN表示某一段河的两岸，EF∥MN．综合实践课上，同学们需要在河岸MN上测量这段河的宽度（EF与MN之间的距离），已知河对岸EF上有建筑物C、D，且CD＝60米，同学们首先在河岸MN上选取点A处，用测角仪测得C建筑物位于A 北偏东45°方向，再沿河岸走20米到达B处，测得D建筑物位于B北偏东55°方向，请你根据所测数据求出该段河的宽度，（用非特殊角的三角函数或根式表示即可）【解答】解：如图，过C、D分别作CP⊥MN、DQ⊥MN垂足为P、Q，设河宽为x米．由题意知，△ACP为等腰直角三角形，∴AP＝CP＝x（米），BP＝x﹣20（米），在Rt△BDQ中，∠BDQ＝55°，∴，∴tan55°⋅x＝x+40，∴（tan55°﹣1）⋅x＝40，∴，所以河宽为米．答：河宽为米．12．小明在A点测得C点在A点的北偏西75°方向，并由A点向南偏西45°方向行走到达B点测得C点在B点的北偏西45°方向，继续向正西方向行走2km后到达D点，测得C 点在D点的北偏东22.5°方向，求A，C两点之间的距离．（结果保留0.1km．参数数据≈1.732）【解答】解：过点A作AM∥BD，过B点作BM⊥BD，AM与BM交于点M，∵在A点测得C点在A点的北偏西75°方向，∴∠NAC＝75°，∴∠CAM＝15°，∵由A点向南偏西45°方向行走到达B点，∴∠MAB＝45°，∴∠MBA＝45°，∵C点在B点的北偏西45°方向，∴∠CBM＝45°，∴∠CBA＝90°，∠CBD＝45°，∵C点在D点的北偏东22.5°方向，∴∠PDC＝22.5°，∴∠DCB＝67.5°，∴∠BDC＝180°﹣67.5°﹣45°＝67.5°，∴BD＝BC，由题可得DB＝2km，∴BC＝2km，在Rt△ABC中，∠CAB＝15°+45°＝60°，BC＝2，∴AC＝≈1.3km．13．如图，一段河流自西向东，河岸笔直，且两岸平行．为测量其宽度，小明在南岸边B处测得对岸边A处一棵大树位于北偏东60°方向，他以1.5m/s的速度沿着河岸向东步行40s后到达C处，此时测得大树位于北偏东45°方向，试计算此段河面的宽度（结果取整数，参考数据：≈1.732）【解答】解：如图，作AD⊥BC于D．由题意可知：BC＝1.5×40＝60（m），∠ABD＝90°﹣60°＝30°，∠ACD＝90°﹣45°＝45°，在Rt△ACD中，∵tan∠ACD＝tan45°＝＝1，∴AD＝CD，在Rt△ABD中，∵tan∠ABD＝tan30°＝，∴BD＝，∵BC＝BD﹣CD＝﹣AD＝60（m），∴AD＝30（+1）≈82（m），答：此段河面的宽度约82m．14．时代中学组织学生进行红色研学活动．学生到达爱国主义教育基地后，先从基地门口A 处向正南方向走300米到达革命纪念碑B处，再从B处向正东方向走到党史纪念馆C处，然后从C处向北偏西37°方向走200米到达人民英雄雕塑D处，最后从D处回到A处．已知人民英雄雕塑在基地门口的南偏东65°方向，求革命纪念碑与党史纪念馆之间的距离（精确到1米）．（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75，sin65°≈0.91，cos65°≈0.42，tan65°≈2.14）【解答】解：过D作DE⊥AB于E，DF⊥BC于F，如图所示：由题意得：∠CDF＝37°，CD＝200米，在Rt△CDF中，sin∠CDF＝＝sin37°≈0.60，cos∠CDF＝＝cos37°≈0.80，∴CF≈200×0.60＝120（米），DF≈200×0.80＝160（米），∵AB⊥BC，DF⊥BC，DE⊥AB，∴∠B＝∠DFB＝∠DEB＝90°，∴四边形BFDE是矩形，∴BF＝DE，BE＝DF＝160米，∴AE＝AB﹣BE＝300﹣160＝140（米），在Rt△ADE中，tan∠DAE＝＝tan65°≈2.14，∴DE≈AE×2.14＝140×2.14＝299.60（米），∴BF＝DE≈299.60（米），∴BC＝BF+CF＝299.60+120≈420（米），答：革命纪念碑与党史纪念馆之间的距离约为420米．15．如图，一艘货船在灯塔C的正南方向，距离灯塔257海里的A处遇险，发出求救信号．一艘救生船位于灯塔C的南偏东40°方向上，同时位于A处的北偏东60°方向上的B处，救生船接到求救信号后，立即前往救援．求AB的长（结果取整数）参考数据：tan40°≈0.84，取1.73．【解答】解：如图，过点B作BH⊥AC，垂足为H，由题意得，∠BAC＝60°，∠BCA＝40°，AC＝257海里，在Rt△ABH中，∵tan∠BAH＝，cos∠BAH＝，∴BH＝AH•tan60°＝AH，AB＝＝2AH，在Rt△BCH中，∵tan∠BCH＝，∴CH＝＝，又∵CA＝CH+AH，∴257＝+AH，所以AH＝，∴AB＝≈＝168（海里），答：AB的长约为168海里．。

用解直角三角形解方位角的应用【知识与技能】进一步掌握用解直角三角形的知识解决实际问题的方法，体会方位角 的含义及其所代表的实际意义，能用它们进行有关的计算.【过程与方法】通过实际问题的求解，总结出用解直角三角形的知识解决实际问题的一般过程，增强分析问题和解决问题的能力.【情感态度】渗透数形结合的思想方法，增强学生的数学应用意识和能力.【教学重点】用三角函数有关知识解决方位角问题.【教学难点】学会准确分析问题，并将实际问题转化为数学模型.一、复习回顾，新知导引方位角的意义.【教学说明】提出问题顾，为后继学习作好准备.二、典例精析，掌握新知例 如图，一艘海轮位于灯塔P 的北偏东65°方向，距离灯塔80海里的A 处，它沿正南方向航行一段时间后，到达位于灯塔P 的南偏东34°方向上的B 处.这时，海轮所在的B 处距离灯塔P 有多远 (结果取整数）？分析与解 易知P 点正东方向与AC 具有垂直关系，即图中PC 丄AB ，若记垂足为C ，则图现了两个直角三角形APC 和直角三角形BPC.而在Rt △APC中，知AP=80，∠APC=90°-65°=25°，故可求出线段PC 的长，即由APPC =∠APC cos ,得PC=AP · cos25°=80·cos25°≈72.505，因此在Rt △BPC 中，由PBPC PB =∠C cos ，得，13056cos 505.7256cos ≈︒=︒=PC PB 从而可得知海轮在B 处时距离灯塔P 约130海里. 【教学说明】本例的设计较上节课所学过的应用问题不同之处在于用其中一个直角三角形中所获得的结论来作为另一个直角三角形的条件而获得问题的解答，这正是学生感到困难的地方，因而应作为引导，帮助学生进行观察思考.三、师生互动，课堂小结问题 通过学习用解直角三角形知识解决实际问题过程中，你有哪些收获？【教学说明】师生共同探索，完善知识体系.1.布置作业：从教材习题中选取.2.完成创优作业中本课时的“课时作业”部分.本课时应首先认知“方位角”及其所代表的实际意义，然后结合解直角三角形的有关知识加以论证，层层展开，步步深入.--------------------- 赠予---------------------【幸遇•书屋】你来，或者不来我都在这里，等你、盼你等你婉转而至盼你邂逅而遇你想，或者不想我都在这里，忆你、惜你忆你来时莞尔惜你别时依依你忘，或者不忘我都在这里，念你、羡你念你袅娜身姿羡你悠然书气人生若只如初见任你方便时来随你心性而去却为何，有人为一眼而愁肠百转为一见而不远千里晨起凭栏眺但见云卷云舒风月乍起春寒已淡忘如今秋凉甚好几度眼迷离感谢喧嚣把你高高卷起砸向这一处静逸惊翻了我的万卷和其中的一字一句幸遇只因这一次被你拥抱过，览了被你默诵过，懂了被你翻开又合起被你动了奶酪和心思不舍你的过往和过往的你记挂你的现今和现今的你遐想你的将来和将来的你难了难了相思可以这一世--------------------- 谢谢喜欢--------------------。