随机变量及其分布期末练习题及答案

第二章 随机变量及其分布习题一 、填空题1. 设随机变量ξ的分布律为NaK P ==)(ξ（K=1,2, N ）,则常数=a 。

2. 盒内有5个零件，其中2件次品，从中任取3件，用ξ表示取出的次品数，则ξ的概率分布为 。

3.设)(x F 是离散型随机变量的分布函数，若______)(==b P ξ，则)()()(a F b F b a P -=<<ξ成立。

4.设离散型随机变量ξ的分布函数为 ⎝⎛≥+<≤-<≤--<=221321110)(x b a x a x ax x F ，且21)2(==ξP ，则___________________,______,的分布律为ξ==b a5. 设连续型随机变量ξ的概率密度为⎪⎩⎪⎨⎧≤>=-00)(2x x kex f x则 ____)2(____,)2(____,)21(___,=<===≤<=ξξξP P P k6. 设5个晶体管中有2个次品，3个正品，如果每次从中任取1个进行测试，测试后的产品不放回，直到把2个次品都找到为止，则需要进行的测试次数ξ是一个随机变量，则________)2(______,)5(=≤==ξξP P7. 设随机变量ξ的概率密度为8)1(2)(--=x kex f （+∞<<∞-x ），则=k 。

8. 两个随机变量ηξ，相互独立的充要条件是______9. 设连续型随机变量ξ的概率密度为⎩⎨⎧<≥=-0)(x x e x f x，则ξ的函数ξη=的概率密度________)(=y ηϕ 10. 设随机变量ξ的概率密度为⎩⎨⎧>><<=其他)0,0(,10)(k b x kx x f b，且________________,,75.0)21(===>b k P 则ξ 二 、选择题1 .kk p x P 2)(==ξ)2,1( =k 为一随机变量ξ的分布律的必要条件是（ ） （A ）k x 非负 （B ）k x 为整数（C ）20≤≤k p （D ）2≥k p 2 . 若函数)(x f y =是一随机变量ξ的概率密度，则（ ）一定成立（A ）)(x f 的定义域为[0，1] （B ）)(x f 的值域为[0，1] (C) )(x f 非负(D) )(x f 在），（∞∞-内连续 3.如果)(x F 是（ ），则)(x F 一定不可以是连续型随机变量的分布函数（ ） （A ）非负函数 （B ）连续函数 （C ）有界函数 （D ）单调减少函数 4.下列函数中，（ ）可以作为连续型随机变量的分布函数(A))(x F = ⎩⎨⎧≥<010x x e x（B ）G(x)= ⎩⎨⎧≥<-01x x e x(C)=Φ)(x ⎩⎨⎧≥-<0100x ex x(D) H(x)= ⎩⎨⎧≥+<-0100x ex x5 . 设）（ηξ, 的联合概率密度为⎪⎩⎪⎨⎧≤+=其他11),(22y x y x f π则ηξ与为（ ）的随机变量（A ）独立同分布 （B ）独立不同分布（C ）不独立同分布 （D ）不独立也不同分布三、计算题1. 掷两颗骰子，用ξ表示点数之和，求ξ的概率分布。

随机变量及其分布期末练习题及答案1．在事件A 发生的概率为p 的伯努利试验中，若以ξ记第r 次A 发生时的试验的次数，求ξ的分布。

[解] {}发生次试验次而第恰好出现了次试验中前A k r A k P k P 11-)(-==ξ),1,(,)1()1(11111Λ+=-=⋅-=-------r r k p p C p p p C r k r r k r k r r k小结 求离散型随机变量的分布律时，首先应该搞清随机变量取可能值时所表示的随机事件，然后确定其分布列。

为验证所求分布是否正确，通常可计算一下所求得的“分布列”之和是否为1，若不是，则结果一定是错误的。

2．设随机变量X 的分布函数为⎪⎩⎪⎨⎧>≤≤<=.1,1;10.0,1)(2x x Ax x x F求（1）A 的值；（2）X 落在)21,1(-及)2,31(内的概率；（3）X 的概率密度函数。

[解] （1）有分布函数的右连续性， 在1=x 点处有1)01()1(=+==F A F ，即1=A（2）由分布函数的性质知，41)1()21())21,1((=--=-∈F F X P ； 98311)31()2())2,31((2=⎪⎭⎫ ⎝⎛-=-=-∈F F X P ； （3）由于)(x F 最多除1=x 和0点外处处可导，且在1,0=x 处连续，若取⎩⎨⎧≤≤><=.10,2;10,0)(x x x x x f 或 则0)(≥x f ，且对一切x 有⎰∞-=x dt t f x F )()(，从而)(x f 为随机变量X 的密度函数。

3．设),2(~2σN X ，且3.0)42(=<<X P ，求)0(<X P[解] 因为 )0(2)42(3.0Φ-⎪⎭⎫ ⎝⎛Φ=<<=σX P 所以 8.05.03.02=+=⎪⎭⎫ ⎝⎛Φσ于是 2.0212202)0(=⎪⎭⎫ ⎝⎛Φ-=⎪⎭⎫ ⎝⎛-Φ=⎪⎭⎫ ⎝⎛-<-=<σσσσX P X P 4．一批鸡蛋，优良品种占三分之二，一般品种占三分之一，优良品种蛋重（单位：克）)5,55(~21N X ，一般品种蛋重)5,45(~22N X 。

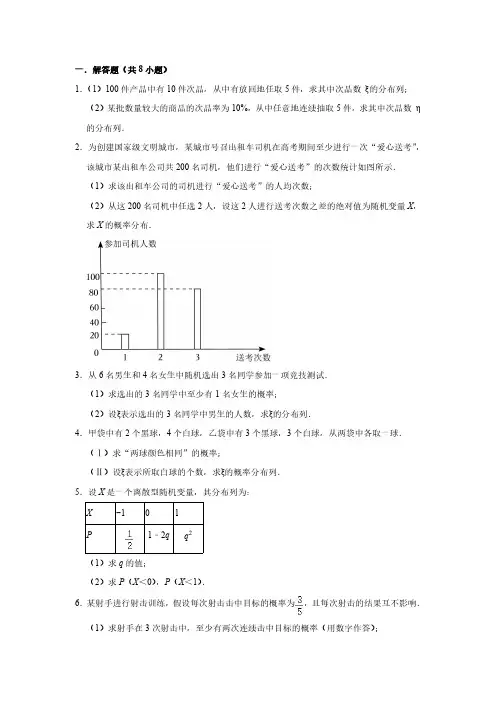
一．解答题（共8小题）1．（1）100件产品中有10件次品，从中有放回地任取5件，求其中次品数ξ的分布列；（2）某批数量较大的商品的次品率为10%，从中任意地连续抽取5件，求其中次品数η的分布列．2．为创建国家级文明城市，某城市号召出租车司机在高考期间至少进行一次“爱心送考”，该城市某出租车公司共200名司机，他们进行“爱心送考”的次数统计如图所示．（1）求该出租车公司的司机进行“爱心送考”的人均次数；（2）从这200名司机中任选2人，设这2人进行送考次数之差的绝对值为随机变量X，求X的概率分布．3．从6名男生和4名女生中随机选出3名同学参加一项竞技测试．（1）求选出的3名同学中至少有1名女生的概率；（2）设ξ表示选出的3名同学中男生的人数，求ξ的分布列．4．甲袋中有2个黑球，4个白球，乙袋中有3个黑球，3个白球，从两袋中各取一球．（Ⅰ）求“两球颜色相同”的概率；（Ⅱ）设ξ表示所取白球的个数，求ξ的概率分布列．5．设X是一个离散型随机变量，其分布列为：X−101P1﹣2q q2（1）求q的值；（2）求P（X＜0），P（X＜1）．6．某射手进行射击训练，假设每次射击击中目标的概率为，且每次射击的结果互不影响．（1）求射手在3次射击中，至少有两次连续击中目标的概率（用数字作答）；（2）求射手第3次击中目标时，恰好射击了4次的概率（用数字作答）；（3）设随机变量ξ表示射手第3次击中目标时已射击的次数，求ξ的分布列．7．袋中有3个红球，4个黑球，从袋中任取4个球．（1）求红球个数X的分布列；（2）若取到一个红球得2分，取到一个黑球得1分，求得分不小于6分的概率．8．从5名男生和3名女生中任选2人去参加学校组织的“低碳杯”知识抢答赛，用ξ表示选出的女生的人数．（1）求随机变量ξ的分布列；（2）求事件“选出的2学生至少有一女生”的概率．参考答案与试题解析一．解答题（共8小题）1．（1）100件产品中有10件次品，从中有放回地任取5件，求其中次品数ξ的分布列；（2）某批数量较大的商品的次品率为10%，从中任意地连续抽取5件，求其中次品数η的分布列．【解答】解：（1）由题意知ξ的可能取值为0，1，2，3，4，5，每次取出次品的概率为：，相当于5次独立重复实验，ξ～B（5，），P（ξ＝0）＝＝0.59059，P（ξ＝1）＝＝0.32805，P（ξ＝2）＝＝0.07329，P（ξ＝3）＝＝0.0081，P（ξ＝4）＝＝0.00045，P（ξ＝5）＝＝0.00001，∴ξ的分布列为：ξ012345P0.590590.328050.07290.00810.000450.00001（2）由题意知η的可能取值为0，1，2，3，4，5，且η～B（5，0.1），∴η的分布列为：η012345P0.590590.328050.07290.00810.000450.000012．为创建国家级文明城市，某城市号召出租车司机在高考期间至少进行一次“爱心送考”，该城市某出租车公司共200名司机，他们进行“爱心送考”的次数统计如图所示．（1）求该出租车公司的司机进行“爱心送考”的人均次数；（2）从这200名司机中任选2人，设这2人进行送考次数之差的绝对值为随机变量X，求X的概率分布．【解答】解：（1）由统计图得200名司机中送考1次的有20人，送考2次的有100人，送考3次的有80人，∴该出租车公司的司机进行“爱心送考”的人均次数为；（2）从该公司任选两名司机，记“这两人中﹣人送考1次，另一人送考2次”为事件A，“这两人中一人送考2次，另一人送考3次“为事件B，“这两人中﹣人送考1次，另一人送考3次”为事件C，“这两人送考次数相同”为事件D，由题意知X的所有可能取值为0，1，2，，，，所以X的分布列为：X012P3．从6名男生和4名女生中随机选出3名同学参加一项竞技测试．（1）求选出的3名同学中至少有1名女生的概率；（2）设ξ表示选出的3名同学中男生的人数，求ξ的分布列．【解答】解：（1）由意可知，选出的3名同学全是男生的概率为＝，∴选出的3名同学中至少有1名女生的概率为P＝1﹣＝．（2）根据题意，ξ的可能取值为0，1，2，3，P（ξ＝0）＝＝，P（ξ＝1）＝＝，P（ξ＝2）＝＝，P（ξ＝3）＝＝，∴ξ的分布列为：ξ0123P4．甲袋中有2个黑球，4个白球，乙袋中有3个黑球，3个白球，从两袋中各取一球．（Ⅰ）求“两球颜色相同”的概率；（Ⅱ）设ξ表示所取白球的个数，求ξ的概率分布列．【解答】解：（I）从甲中取出黑球的概率为，取出白球的概率为，从乙中取出黑球的概率为，取出白球的概率为，故“两球颜色相同”的概率P＝．（II）由题意可得，ξ所有可能取值为0，1，2，P（ξ＝0）＝＝，P（ξ＝1）＝，P（ξ＝2）＝，故ξ的分布列为：ξ012P5．设X是一个离散型随机变量，其分布列为：X−101P1﹣2q q2（1）求q的值；（2）求P（X＜0），P（X＜1）．【解答】解：（1）依题意，得，解得或（舍去），所以．（2）由（1）得，，所以，．6．某射手进行射击训练，假设每次射击击中目标的概率为，且每次射击的结果互不影响．（1）求射手在3次射击中，至少有两次连续击中目标的概率（用数字作答）；（2）求射手第3次击中目标时，恰好射击了4次的概率（用数字作答）；（3）设随机变量ξ表示射手第3次击中目标时已射击的次数，求ξ的分布列．【解答】解：（1）设事件该射手第i次射击，击中目标为A i，i＝1，2，3，则，所以，事件射手在3次射击中，至少有两次连续击中目标可表示为，因为事件，，A1A2A3互斥，所以又事件A1，A2，A3相互独立，所以＝＝；（2）事件射手第3次击中目标时，恰好射击了4次等于事件前3次中恰好击中两次目标且第四次击中目标，又各次击中目标的概率为，所以前3次中恰有两次击中目标的概率为，第四次击中目标的概率为，所以事件射手第3次击中目标时，恰好射击了4次的概率；（3）由已知ξ的取值有3，4，5，⋅⋅⋅，n，⋅⋅⋅，又，，，⋅⋅⋅，，所以随机变量ξ的分布列为：ξ345…n…P……7．袋中有3个红球，4个黑球，从袋中任取4个球．（1）求红球个数X的分布列；（2）若取到一个红球得2分，取到一个黑球得1分，求得分不小于6分的概率．【解答】解：（1）由题意可得，X可能取值为0，1，2，3，P（X＝0）＝，P（X＝1）＝，P（X＝2）＝，P（X＝3）＝，故X的分布列为：X0123P（2）设得分为Y，则得分Y可以取4，5，6，7，分别对应4个黑球，3黑1红，2黑2红，1黑3红四种情况，P（Y≥6）＝P（Y＝6）+P（Y＝7）＝，故得分不小于6分的概率为．8．从5名男生和3名女生中任选2人去参加学校组织的“低碳杯”知识抢答赛，用ξ表示选出的女生的人数．（1）求随机变量ξ的分布列；（2）求事件“选出的2学生至少有一女生”的概率．【解答】解：（1）由题意得ξ的可能取值为0，1，2，P（ξ＝0）＝＝，P（ξ＝1）＝＝，P（ξ＝2）＝＝，∴随机变量ξ的分布列为：ξ012P（2）事件“选出的2学生至少有一女生”的概率为：P＝P（ξ＝1）+P（ξ＝2）＝＝．。

第二章 随机变量及其分布18.[十七] 设随机变量X 的分布函数为⎪⎩⎪⎨⎧≥<≤<=.,1,1,ln ,1,0)(e x e x x x x F X ，求（1）P (X<2), P {0<X ≤3}, P (2<X<25)；（2）求概率密度f X (x ). 解：（1）P (X ≤2)=F X (2)= ln2， P (0<X ≤3)= F X (3)－F X (0)=1，45ln 2ln 25ln )2()25(252(=-=-=<<X X F F X P （2）⎪⎩⎪⎨⎧<<==其它,0,1,1)(')(e x x x F x f24.[二十二] 设K 在（0，5）上服从均匀分布，求方程02442=+++K xK x 有实根的概率∵ K 的分布密度为：⎪⎩⎪⎨⎧<<-=其他50051)(K K f要方程有根，就是要K 满足(4K )2－4×4× (K+2)≥0。

解不等式，得K ≥2时，方程有实根。

∴53051)()2(5522=+==≥⎰⎰⎰∞+∞+dx dx dx x f K P 25.[二十三] 设X ～N （3.22）（1）求P (2<X ≤5)，P (－4)<X ≤10)，P {|X|>2}，P (X>3)∵ 若X ～N （μ，σ2），则P (α<X ≤β)=φ-⎪⎭⎫ ⎝⎛-σμβφ⎪⎭⎫ ⎝⎛-σμα ∴P (2<X ≤5) =φ-⎪⎭⎫ ⎝⎛-235φ⎪⎭⎫ ⎝⎛-232=φ(1)－φ(－0.5) =0.8413－0.3085=0.5328P (－4<X ≤10) =φ-⎪⎭⎫ ⎝⎛-2310φ⎪⎭⎫ ⎝⎛--234=φ(3.5)－φ(－3.5) =0.9998－0.0002=0.9996P (|X |>2)=1－P (|X |<2)= 1－P (－2< P <2 )=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛--Φ-⎪⎭⎫ ⎝⎛-Φ-2322321 =1－φ(－0.5) +φ(－2.5) =1－0.3085+0.0062=0.6977P (X >3)=1－P (X ≤3)=1－φ⎪⎭⎫⎝⎛-233=1－0.5=0.5（2）决定C 使得P (X > C )=P (X ≤C )∵P (X > C )=1－P (X ≤C )= P (X ≤C )得 P (X ≤C )=21=0.5 又P (X ≤C )=φ023,5.023=-=⎪⎭⎫ ⎝⎛-C C 查表可得∴ C =3 28.[二十六] 一工厂生产的电子管的寿命X （以小时计）服从参数为μ=160，σ(未知)的正态分布，若要求P (120＜X ≤200＝=0.80，允许σ最大为多少？∵ P (120＜X ≤200)=80.04040160120160200=⎪⎭⎫ ⎝⎛-Φ-⎪⎭⎫ ⎝⎛Φ=⎪⎭⎫ ⎝⎛-Φ-⎪⎭⎫ ⎝⎛-Φσσσσ 又对标准正态分布有φ(－x )=1－φ(x )∴ 上式变为80.040140≥⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛Φ--⎪⎭⎫ ⎝⎛Φσσ 解出9.040:40≥⎪⎭⎫ ⎝⎛Φ⎪⎭⎫ ⎝⎛Φσσ便得 再查表，得25.31281.140281.140=≤≥σσ 31.[二十八] 设随机变量X 在（0，1）上服从均匀分布 （1）求Y=e X 的分布密度∵ X 的分布密度为：⎩⎨⎧<<=为其他x x x f 0101)(Y=g (X ) =e X 是单调增函数 又 X=h (Y )=lnY ，反函数存在且α = min [g (0), g (1)]=min (1, e )=1=βmax [g (0), g (1)]=max (1, e )= e∴ Y 的分布密度为：⎪⎩⎪⎨⎧<<⋅=⋅=为其他y e y yy h y h f y ψ0111|)('|)]([)(（2）求Y=－2lnX 的概率密度。

随机变量及其分布(总分102, 做题时间90分钟)一、单项选择题(每题的备选项中，只有1个最符合题意)1.下列关于“右偏分布”的表述错误的是( )。

SSS_SINGLE_SELA 右偏分布是正态分布的形式之一B 符合右偏分布的随机变量大量取值在左边，少量分布在右边C 符合右偏分布的随机变量少量取值在左边，大量分布在右边D 随机变量的分布很散分值: 1答案:B[解析] 对数正态分布的特点之一就是“右偏分布”，符合右偏分布的随机变量的取值大量在左边，少量取值在右边，并且很分散。

2.对于产品的某个质量特性X的不合格品率，在计算之前需要知道的条件有( )。

SSS_SINGLE_SELA产品质量特性X的分布，在过程受控情况下X的分布常为正态分布(μ，σ2)，这是稳定过程的概括B 某个公认标准对产品特性的要求C 企业对产品下达的任务书D X低于下规范限的概率和X高于上规范限的概率分值: 1答案:A[解析] 产品某个质量特性X的不合格品率的计算要知道两件事：①质量特性X 的分布，在过程受控情况下，X的分布常为正态分布N(μ，σ2)，这是稳定过程的概括；②产品的规格限，包括上规格限TU 和下规格限TL。

3.设某二项分布的均值等于3，方差等于2.7，则二项分布参数P=( )。

SSS_SINGLE_SELA 0.1B 0.3C 0.7D 0.9分值: 1答案:A[解析] 此二项分布记为b(n，p)，则E(X)=np，Var(X)=np(1-p)，根据题意，代入数据可得np=3，np(1-p)=2.7，所以p=0.1。

4.对下列常见密度函数所对应的方差的形式正确的一项是( )。

SSS_SINGLE_SELA 两点分布b(1,的方差：np(1-B 超几何分布h(n，N，的方差：n(N-/(N-1)&#8226;(M/(1-(M/)C均匀分布U(a，的方差：(b+ 2/12D对数正态分布LN(μ，σ2)的方差：分值: 1答案:B[解析] A项两点分布的方差为p(1-p)；C项均匀分布的方差为(b-a)2/12；D项对数正态分布的方差为。

第二章 随机变量及其分布一. 填空题1. 设随机变量X ～B(2, p), Y ～B(3, p), 若P(X ≥ 1) =95, 则P(Y ≥ 1) = _________. 解. 94951)1(1)0(=-=≥-==X P X P 94)1(2=-p , 31=p 2. 已知随机变量X 只能取－1, 0, 1, 2四个数值, 其相应的概率依次为cc c c 162,85,43,21, 则c = ______. 解. 2,16321628543211==+++=c cc c c c 3. 用随机变量X 的分布函数F(x)表示下述概率:P(X ≤ a) = ________. P(X = a) = ________.P(X > a) = ________. P(x 1 < X ≤ x 2) = ________.解. P(X ≤ a) = F(a) P(X = a) = P(X ≤ a)－P(X < a) = F(a)－F(a －0) P(X > a) = 1－F(a) P(x 1 < X ≤ x 2) = F(x 2)－F(x 1)4. 设k 在(0, 5)上服从均匀分布, 则02442=+++k kx x 有实根的概率为_____.解. k 的分布密度为⎪⎩⎪⎨⎧=051)(k f 其它50≤≤kP{02442=+++k kx x 有实根} = P{03216162≥--k k } = P{k ≤－1或k ≥ 2} =535152=⎰dk 5. 已知2}{,}{kbk Y P k a k X P =-===(k = 1, 2, 3), X 与Y 独立, 则a = ____, b = ____, 联合概率分布_____, Z = X + Y 的概率分布为_____. 解. 116,132==++a a a a . 4936,194==++b b b b (X, Y)P24α 66α 251α 126α 72αab = 216α, 5391=α 6. 已知(X, Y)联合密度为⎩⎨⎧+=0)sin(),(y x c y x ϕ 其它4,0π≤≤y x , 则c = ______, Y 的边缘概率密度=)(y Y ϕ______.解.12,1)sin(4/04/0+==+⎰⎰c dxdy y x c ππ所以⎩⎨⎧++=0)sin()12(),(y x y x ϕ 其它4,0π≤≤y x当 40π≤≤y 时所以⎪⎩⎪⎨⎧+-+=0))4cos()(cos 12()(y y y Y πϕ 其它40π≤≤y7. 设平面区域D 由曲线2,1,01e x x y xy ====及直线围成, 二维随机变量(X, Y)在D 上服从均匀分布, 则(X, Y)关于X 的边缘密度在x = 2处的值为_______. 解. D 的面积 =2121=⎰e dx x. 所以二维随机变量(X, Y)的密度为: 下面求X 的边沿密度: 当x < 1或x > e 2时 当1 ≤ x ≤ e 2时 ⎰⎰===∞+∞-x X x dy dy y x x 102121),()(ϕϕ, 所以41)2(=X ϕ. 8. 若X 1, X 2, …, X n 是正态总体N(μ, σ2)的一组简单随机样本, 则)(121n X X X nX +++=Λ服从______. 解. 独立正态分布随机变量的线性函数服从正态分布.μ==⎪⎭⎫ ⎝⎛∑∑==n i i n i i X E n X n E 11)(11, nX D nX n D ni in i i 2121)(11σ==⎪⎭⎫ ⎝⎛∑∑==所以 ),(~2nN X σμ9. 如果(X, Y)的联合分布用下列表格给出,且X 与Y 相互独立, 则α = ______, β = _______.解.两式相除得βαβα=++18191, 解得 βα2=, 92,91==αβ.10. 设(X, Y)则 i. Z = X + Y iii. U= X 2 + Y －2的分布律_______. 解.二. 单项选择题1. 如下四个函数哪个是随机变量X 的分布函数(A)⎪⎪⎩⎪⎪⎨⎧=221)(x F 0022≥<≤--<x x x , (B) ⎪⎩⎪⎨⎧=1sin 0)(x x F ππ≥<≤<x x x 00(C) ⎪⎩⎪⎨⎧=1sin 0)(x x F 2/2/00ππ≥<≤<x x x , (D) ⎪⎪⎩⎪⎪⎨⎧+=1310)(x x F 212100≥<≤<x x x解. (A)不满足F(+∞) = 1, 排除(A); (B)不满足单增, 排除(B); (D)不满足F(1/2 + 0) = F(1/2), 排除(D); (C)是答案. 2. ),4,2,0(!/)(Λ===-k k ec k X P kλλ是随机变量X 的概率分布, 则λ, c 一定满足(A) λ > 0 (B) c > 0 (C) c λ > 0 (D) c > 0, 且 λ > 0 解. 因为),4,2,0(!/)(Λ===-k k ec k X P kλλ, 所以c > 0. 而k 为偶数, 所以λ可以为负.所以(B)是答案.3. X ～N(1, 1), 概率密度为ϕ(x), 则(A)5.0)0()0(=≥=≤X P X p (B)),(),()(+∞-∞∈-=x x x ϕϕ (C) 5.0)1()1(=≥=≤X P X p (D) ),(),(1)(+∞-∞∈--=x x F x F 解. 因为E(X) = μ = 1, 所以5.0)1()1(=≥=≤X P X p . (C)是答案.4. X, Y 相互独立, 且都服从区间[0, 1]上的均匀分布, 则服从区间或区域上的均匀分布的随机变量是(A) (X, Y) (B) X + Y (C) X 2 (D) X －Y解. X ～⎩⎨⎧=01)(x ϕ 其它10≤≤x , Y ～⎩⎨⎧=01)(y ϕ 其它10≤≤y . 所以(X, Y)～⎩⎨⎧=01),(y x ϕ其它1,0≤≤y x .所以(A)是答案.5. 设函数⎪⎪⎩⎪⎪⎨⎧=120)(xx F 1100>≤<≤x x x 则(A) F(x)是随机变量X 的分布函数. (B) 不是分布函数.(C) 离散型分布函数. (D)连续型分布函数.解. 因为不满足F(1 + 0) = F(1), 所以F(x)不是分布函数, (B)是答案.6. 设X, Y 是相互独立的两个随机变量, 它们的分布函数为)(),(y F x F Y X , 则Z = max(X, Y)的分布函数是(A) )(z F Z = max{)(),(z F z F Y X } (B) )(z F Z = max{|)(||,)(|z F z F Y X } (C) )(z F Z = )()(z F z F Y X (D) 都不是解. }{}),{m ax ()()(z Y z X P z Y X P z Z P z F Z ≤≤=≤=≤=且 )()()()(z F z F z Y P z X P Y X =≤≤因为独立. (C)是答案.7. 设X, Y 是相互独立的两个随机变量, 其分布函数分别为)(),(y F x F Y X , 则Z = min(X, Y)的分布函数是(A) )(z F Z = )(z F X (B) )(z F Z = )(z F Y(C) )(z F Z = min{)(),(z F z F Y X } (D) )(z F Z = 1－[1－)(z F X ][1－)(z F Y ] 解. }{1}),{m in(1)(1)()(z Y z X P z Y X P z Z P z Z P z F Z >>-=>-=>-=≤=且 (D)是答案.8. 设X 的密度函数为)(x ϕ, 而,)1(1)(2x x +=πϕ 则Y = 2X 的概率密度是(A))41(12y +π (B) )4(22y +π (C) )1(12y +π (D) y arctan 1π解. )2()2(}2{)()(yF y X P y X P y Y P y F X Y =≤=≤=≤= (B)是答案.9. 设随机变量(X, Y)的联合分布函数为⎩⎨⎧=+-0),()(y x e y x ϕ 其它0,0>>y x , 则2YX Z +=的分布密度是(A) ⎪⎩⎪⎨⎧=+-021)()(y x Z e Z ϕ 其它0,0>>y x (B) ⎪⎩⎪⎨⎧=+-0)(2y x Z e z ϕ 其它0,0>>y x(C) ⎩⎨⎧=-04)(2z Z ze Z ϕ 00≤>z z (D) ⎪⎩⎪⎨⎧=-021)(zZ eZ ϕ 00≤>z z解. 2YX Z +=是一维随机变量, 密度函数是一元函数, 排除(A), (B). 21210=⎰∞+-dz e z , 所以(D)不是答案. (C)是答案.注: 排除法做单项选择题是经常使用而且很有效的方法. 该题也可直接计算Z 的密度: 当z < 0时 当z ≥ 0时 =12222020+--=⎥⎦⎤⎢⎣⎡-----⎰⎰z z z x z y x e ze dx dy e e ==)()('z F z ZZ ϕ⎩⎨⎧-042z ze 00≤>z z , (C)是答案.10. 设两个相互独立的随机变量X 和 Y 分别服从正态分布N(0, 1)和N(1, 1), 则下列结论正确的是(A) P{X + Y ≤ 0} = 1/2 (B) P{X + Y ≤ 1} = 1/2 (C) P{X －Y ≤ 0} = 1/2 (D) P{X －Y ≤ 1} = 1/2解. 因为X 和 Y 分别服从正态分布N(0, 1)和N(1, 1), 且X 和 Y 相互独立, 所以 X + Y ～ N(1, 2), X －Y ～ N(－1, 2) 于是P{X + Y ≤ 1} = 1/2, (B)是答案.11. 设随机变量X 服从指数分布, 则Y = min{X, 2}的分布函数是(A) 是连续函数 (B) 至少有两个间断点 (C) 是阶梯函数 (D) 恰好有一个间断点 解. 分布函数: 当y ≥ 2时 当0 ≤ y < 2时 当y < 0时于是 ⎪⎩⎪⎨⎧-=-011)(yY e y F λ 0202<<≤≥y y y 只有y = 2一个间断点, (D)是答案.三. 计算题1. 某射手有5发子弹, 射击一次的命中率为0.9, 如果他命中目标就停止射击, 不命中就一直到用完5发子弹, 求所用子弹数X 的分布密度. 解. 假设X 表示所用子弹数. X = 1, 2, 3, 4, 5.P(X = i) = P(前i －1次不中, 第i 次命中) = 9.0)1.0(1⋅-i , i = 1, 2, 3, 4.当i = 5时, 只要前四次不中, 无论第五次中与不中, 都要结束射击(因为只有五发子弹). 所以 P(X = 5) = 4)1.0(. 于是分布律为2. 设一批产品中有10件正品, 3件次品, 现一件一件地随机取出, 分别求出在下列各情形中直到取得正品为止所需次数X 的分布密度.i. 每次取出的产品不放回; ii. 每次取出的产品经检验后放回, 再抽取; iii. 每次取出一件产品后总以一件正品放回, 再抽取.解. 假设A i 表示第i 次取出正品(i = 1, 2, 3,…) i. ii.1310133)()()()()(11111---⎪⎭⎫⎝⎛====k k k k k A P A P A P A A A p k X P ΛΛ, (k = 1, 2, …) iii. 每次抽取后总以一个正品放回3. 随机变量X 的密度为⎪⎩⎪⎨⎧-=01)(2x cx ϕ 其它1||<x , 求: i. 常数c; ii. X 落在)21,21(-内的概率. 解. πππϕ1,22|arcsin 21)(110112====-==⎰⎰-∞+∞-c c cx c dx xc dx x4. 随机变量X 分布密度为i. 2102)(x x -⎪⎩⎪⎨⎧=πϕ 其它1||<x , ii. ⎪⎩⎪⎨⎧-=02)(x x x ϕ 其它2110≤≤<≤x x求i., ii 的分布函数F(x).解. i. 当x ≤ 1时 当－1< x < 1时 当x ≥ 1时所以 ⎪⎪⎩⎪⎪⎨⎧++-=121arcsin 110)(2x x xx F ππ 1111≥<<--≤x x xii. 当x < 0时当0 ≤ x < 1时 当1 ≤ x < 2时 当2 ≤ x 时所以 ⎪⎪⎪⎩⎪⎪⎪⎨⎧-+-=112220)(22x x x x F 221100≥<≤<≤<x x x x 5. 设测量从某地到某一目标的距离时带有的随机误差X 具有分布密度函数⎪⎪⎭⎫ ⎝⎛--=3200)20(exp 2401)(2x x πϕ, －∞ < x < +∞ 试求: i. 测量误差的绝对值不超过30的概率;ii. 接连独立测量三次, 至少有一次误差的绝对值不超过30的概率.解. 因为⎪⎪⎭⎫ ⎝⎛--=3200)20(exp 2401)(2x x πϕ, －∞ < x < +∞, 所以X ～N(20, 402).i. {}⎭⎬⎫⎩⎨⎧<-<-=<<-=<25.0402025.13030)30|(|X P X P X P 18944.05987.0-+== 0.4931.(其中Φ(x)为N(0, 1)的分布函数)ii. P(至少有一次误差的绝对值不超过30) = 1－P(三次误差的绝对值都超过30) =88.012.01)4931.0(13=-=-6. 设电子元件的寿命X 具有密度为问在150小时内, i. 三只元件中没有一只损坏的概率是多少? ii. 三只电子元件全损坏的概率是多少? iii. 只有一个电子元件损坏的概率是多少?解. X 的密度⎪⎩⎪⎨⎧=0100)(2x x ϕ 100100≤<x x . 所以31100)150(1501002==<⎰dx x X P . 令p = P(X ≥ 150) = 1－31= 32.i. P(150小时内三只元件没有一只损坏) =2783=p ii. P(150小时内三只元件全部损坏) =271)1(3=-piii. P(150小时内三只元件只有一只损坏) =943231213=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛c 7. 对圆片直径进行测量, 其值在[5, 6]上服从均匀分布, 求圆片面积的概率分布. 解. 直径D 的分布密度为⎩⎨⎧=01)(d ϕ其它65≤≤d假设42D X π=, X 的分布函数为F(x).当x ≤ 0时, F(x) = 0 当x > 0时当时即425,54ππ<<x xF(x) = 0 当时即πππ925,645≤≤≤≤x x=54145-=⎰ππxdt x当 x > 9π时所以 ⎪⎪⎩⎪⎪⎨⎧-=1540)(πxx Fππππ99425425>≤≤<x x x 密度⎪⎩⎪⎨⎧==01)(')(x x F x πϕ 其它ππ9425≤≤x8. 已知X 服从参数 p = 0.6的0－1分布在X = 0, X = 1下, 关于Y 的条件分布分别为表1、表2所示表1 表2Y 1 2 3 Y 1 2 3 P(Y|X = 0)41 21 41 P(Y|X = 1) 21 61 31 求(X, Y)的联合概率分布, 以及在Y ≠ 1时, 关于X 的条件分布.解. X 的分布律为(X, Y)所以Y 的分布律为所以9. 设随机变量X 与Y 相互独立, 并在区间[0, 9]上服从均匀分布, 求随机变量YXZ =的分布密度.解. X ～⎪⎩⎪⎨⎧=091)(x X ϕ 其它90≤≤x , Y ～⎪⎩⎪⎨⎧=091)(x Y ϕ 其它90≤≤y因为X, Y 相互独立, 所以(X, Y)联合密度为(X, Y)～⎪⎩⎪⎨⎧=0811),(y x ϕ 其它9,0≤≤y x , )()()(z X Y P z Z P z F Z ≤=≤=当 z ≤ 0时0)(=z F Z 当 0 < z < 1时 y = xz (z < 1)D 1当z ≥ 1时zz 211)992181(811-=⋅-⋅=所以 ⎪⎪⎩⎪⎪⎨⎧==2'21210)()(zz F z Z Z ϕ 1100≥<<≤z z z 10. 设(X, Y)的密度为 求: i.)21|(),|(),(=x y x y x X ϕϕϕ, ii. )21|(),|(),(=y x y x y Y ϕϕϕ 解. i.⎰∞+∞-=dy y x x X ),()(ϕϕ当x ≤ 0 或 x ≥ 1时当0 < x < 1时所以 ⎩⎨⎧-=0)1(4)(3x x X ϕ 其它10<<x所以 ⎪⎩⎪⎨⎧---==0)1()1(6)(),()|(3x y x y x y x x y X ϕϕϕ 其它1,0,0<+>>y x y x 所以 ⎩⎨⎧-==0)21(24)21|(y y x y ϕ 其它210<<yii.⎰∞+∞-=dx y x y Y ),()(ϕϕ当y ≤ 0 或 y ≥ 1时当0 < y < 1时所以 ⎩⎨⎧-=0)1(12)(2y y y Y ϕ 其它10<<y所以 ⎪⎩⎪⎨⎧---==0)1()1(2)(),()|(2y y x y y x y x Y ϕϕϕ 其它1,0,0<+>>y x y x页眉内容所以 ⎩⎨⎧-==0)21(4)21|(x y x ϕ 其它210<<x。

第2章 随机变量及其分布（练习、复习题及答案）一、填空题：1.随机变量ξ的分布列为P(ξ=k )=a /N ，(k =1,2,…,N)，则a = 1 .2.射手每次射击击中目标的概率为p ,连续向同一目标射击，直到某一次击中目标为止,则射击次数ξ的分布列为 P(ξ=k )=p (1-p )k -1,k =1,2,….3.随机变量ξ服从参数为(2,p )的二项分布,随机变量η服从参数为(4,p )的二项分布,若P(ξ<1)=4/9,则P(η≥1)=_ 65/81_.4.离散型随机变量ξ的概率分布P(ξ=0)=0.2，P(ξ=1)=0.3，P(ξ=2)=0.5，则P(ξ≤1.5)=__0.5__.5.随机变量ξ的分布列为P(ξ=k )=!k Ckλ,k =0,1,2,…(λ>0)，则C ＝ e -λ. *λλλλe =++++!3!2!11326.随机变量ξ的分布列为P(ξ=k )=k a -λ,k =1,2,…，其中λ>1，则a ＝ λ-1 .7.一实习生用同一台机器接连独立地制造三个同种零件，第i 个零件是不合格品的概率3,2,1,11=+=i i p i ，以ξ表示三个零件中合格品的个数，则P{ξ=2}＝ 11/24 .8.随机变量ξ的分布函数为F(x ),则概率P(ξ≥a )用F(x )表示为__ 1-F(a )__. 9.随机变量ξ的分布函数为F(x )=⎪⎩⎪⎨⎧<≥+--0 0 0)1(1x x ex x ,,,则P(ξ≤1)=_1-2e -1_. 10.随机变量ξ的概率密度函数为f (x )=⎪⎩⎪⎨⎧<-其他,), 0 2A(2x x ,则A=__1/4__.11.连续型随机变量ξ的分布函数为⎪⎪⎩⎪⎪⎨⎧≥<≤<=1, 110,0,0)(F 2x x x x x ,则ξ的概率密度f (x )=⎩⎨⎧<<其他, 1 10,2x x .12.连续型随机变量ξ的分布函数为)0(00,0B A )(F >⎪⎩⎪⎨⎧≤>+=-λλx x ex x ,, ，则常数A =_1 ,B =_-1;P{-1<ξ<1}= 1-e -λ.13.随机变量ξ的分布函数为⎪⎩⎪⎨⎧<≥+-=-0, 00,)1(1)(x x ex x F x ,则相应的概率密度是⎪⎩⎪⎨⎧<≥=-0, 00,)(x x xex f x .14.随机变量ξ在[1,4]上服从均匀分布,现在对进行3次独立试验,则至少有2次观察值大于2的概率为_20/27_.15.随机变量ξ ~N(70,102)，则P(60<ξ<80)=_0.6826_.(已知Φ(1)=0.8413)16.随机变量ξ服从正态分布N(2,σ2),且P(2<ξ<4)=0.3,则P(ξ<0)=_0.2_.17.随机变量服从正态分布N(μ,σ2)，已知P(ξ<9)=0.975，P(ξ<2)=0.062，则P(ξ>6)=_0.3228_. 18.若ξ~N(0,1)，则η=ξ3的密度函数为+∞<<-∞--y e yy,231322132π.19.统考成绩服从正态分布N(70,102),在参加统考的人中,及格者100人(及格分数为60分),则不及格人数约为_19_.二、选择题1.在下列结果中，构成概率分布的是( D ).{}{}{}{}),,(D.P ),,,(C.P ),,(B.P ),,,(A.P 2 132 2 1 032 2 131 2 1 031============k k ξk k ξk k ξk k ξkkkk2.随机变量ξ的概率分布为P(ξ=k )=b λk (k =1,2,…), b >0，则( C ). A.λ为任意正实数 B.λ=b +1 C.b+=11λ D.11-=b λ3.常数b =( B )时，),,( 2 1)1(=+=k k k b p k 为离散型随机变量的概率分布.A.2B.1C.0.5D.34.设ξ是一个离散型随机变量，则( D )可以成为ξ的分布列.{}{}, , , n n en ξn n en ξx x x x x R p p p nn210!32 1!30.22.0 .303.0 .10 ,1 0 1 3354321======⎪⎪⎭⎫⎝⎛∈⎪⎪⎭⎫⎝⎛---.D.P,,.C.P B.A.5.随机变量ξ~N(0,1)，ξ的分布函数为Φ(x )，则P(⎢ξ⎪<1)的值为( B ).A.2[1-Φ(1)]B.2Φ(1)-1C.1-Φ(1)D.1-2Φ(1)6.随机变量ξ~N(0,1)，ξ的分布函数为Φ(x )，则P(⎢ξ⎪>2)的值为( A ). A.2[1-Φ(2)] B.2Φ(2)-1 C.2-Φ(2) D.1-2Φ(2)7.设随机变量ξ的分布函数为F (x )，在下列概率中可表示为F (a +0) - F (a )的是( C ). A.P{ξ≤a } B. P{ξ>a } C. P{ξ=a } D. P{ξ≥a }8.下列函数可以作为某一随机变量ξ的密度函数的是( D ).⎪⎩⎪⎨⎧∈=⎪⎩⎪⎨⎧-∈=⎪⎩⎪⎨⎧∈=⎩⎨⎧∈=其他D. 其他C. 其他B.其他A., 0 ]2,0[,sin )(, 0 ]2,2[,sin )(, 0 ]23,0[,sin )( , 0 ],0[,sin )(πππππx x x f x x x f x x x f x x x f9.设ξ的概率密度为⎪⎩⎪⎨⎧≤>+=0 0 0)(1A )(4x x x x x f ,,，则A=( B ).A.3B.6C.2.5D.4 10.设随机变量ξ的密度函数为f (x )=)(21+∞<<-∞-x ex，则其分布函数的是( B ).⎪⎪⎪⎩⎪⎪⎪⎨⎧≥<≤-<=⎪⎩⎪⎨⎧≥<-=⎪⎪⎩⎪⎪⎨⎧≥-<=⎪⎩⎪⎨⎧≥<=---1, 1 10,2110, 21 )(0, 1 0,211)(0,2110, 21 )( 0, 0 0,21)(x x e x e x F x x e x F x e x e x F x x e x F x xx x xx D. C. B.A.11.设f (x )是一连续型随机变量ξ的密度函数，其表达式为分段函数，则当x ∈( A )时，f (x )=cos x ，其余f (x )=0.]47,23[],0[],2[]2,0[ππππππ D. C. B.A.12.设随机变量ξ服从[0，5]上的均匀分布，则关于t 的方程4t 2+4ξt+ξ+2=0有实根的概率是( B ).A.0.4B.0.6C.1D.1/313.设随机变量ξ~N(μ, 62)，η~ N(μ, 82)，记p 1=P{ξ≤μ-6}，p 2=P{η≥μ+8}，则( A ).A. p 1=p 2B. p 1>p 2C. p 1<p 2D. p 1≤p 2 三、解答题：1.下列表格是概率分布吗？为什么？(1) ξ 1 2 3 4 不是 (2) ξ -1 0 1 4 是 P 0.2 0.3 0.3 0.4 P 0.1 0.2 0.3 0.4 2.求常数C ,使下列函数成为概率分布:P(ξ=k )=Ck ,k =1,2,…, n ； )1(2+=n n C3.随机变量ξ~b (n , p )，已知P(ξ=1)=P(ξ=n -1)，试求 p 与P(ξ=2)的值.p =0.5，P(ξ=2)=122)1(21+-=⎪⎭⎫ ⎝⎛n nnn n C4.随机试验中事件A 发生的概率为p ，把这个试验独立重复地做两次。

第2章 随机变量及其分布习题 21．设有函数⎩⎨⎧≤=其它，,0,0,sin )(πx x x F试说明)(x F 能否是某随机变量的分布函数。

解：不能，易知对21x x <，有：),()(}1{}{}{12221x F x F x X P x X P x X x P -=<-<=<<又)()(,0}{1221x F x F x X x P ≥≥<<，因此)(x F 在定义域内必为单调递增函数。

然而)(x F 在),0(π上不是单调递增函数，所以不是某随机变量的分布函数。

2．－筐中装有7只蓝球，编号为1，2．3，4，5，6，7。

在筐中同时取3只，以X 表示取出的3只当中的最大号码，写出随机变量X 的分布列。

解：X 的可能值为3，4，5，6，7。

在7只篮球中任取3个共有37C 种取法。

}3{=X 表示取出的3只篮球以3为最大值，其余两个数是1，2，仅有这一种情况，故3515673211)3(37=⋅⋅⋅⋅===C X P}4{=X 表示取出的3只篮球以4为最大值，其余两个数可以在1，2，3中任取两个，共有23C 种取法，故35356732113)4(3723=⋅⋅⋅⋅===C C X P 。

}5{=X 表示取出的3只篮球以5为最大值，其余两个数可在1，2，3，4中任取2个，共有24C 种取法，故3565673212134)5(3724=⋅⋅⋅⋅⋅⋅===C C X P ， }6{=X 表示取出的3只篮球以6为最大值，其余两个数可在1，2，3，4，5中任取2个，共有25C 种取法，故35105673212145)6(3725=⋅⋅⋅⋅⋅⋅===C C X P ，}7{=X 表示取出的3只篮球以7为最大值，其余两个数可在1，2，3，4，5，6中任取2个，共有26C 种取法，故35155673212156)7(3726=⋅⋅⋅⋅⋅⋅===C C X P 。

3. 设X 服从)10(-分布，其分布列为,)1(}{1kkp p k X P --== ,1,0=k 求X 的分布函数，并作出其图形。

随机变量及其分布方法总结经典习题及解答一、离散型随机变量及其分布列1、离散型随机变量:对于随机变量可能取的值，可以按一定次序一一列出，这样的随机变量叫做离散型随机变量。

常用大写英文字母X、Y等或希腊字母ξ、η等表示。

2、分布列:设离散型随机变量ξ可能取得值为：x1，x2，…，x3，…，ξ取每一个值xi（i=1，2，…）的概率为，则称表ξx1x2…xi…PP1P2…Pi…为随机变量ξ的分布列3、分布列的两个性质：⑴Pi≥0，i＝1，2，… ⑵P1+P2+…=1、常用性质来判断所求随机变量的分布列是否正确！二、热点考点题型考点一: 离散型随机变量分布列的性质1、随机变量ξ的概率分布规律为P(ξ＝n)＝(n＝1，2，3，4)，其中a是常数，则P(＜ξ＜)的值为A、B、C、D、答案：D考点二：离散型随机变量及其分布列的计算2、有六节电池，其中有2只没电，4只有电，每次随机抽取一个测试，不放回，直至分清楚有电没电为止，所要测试的次数为随机变量，求的分布列。

解：由题知2，3，4，5∵ 表示前2只测试均为没电，∴ ∵ 表示前两次中一好一坏，第三次为坏，∴ ∵ 表示前四只均为好，或前三只中一坏二好，第四个为坏，∴ ∵ 表示前四只三好一坏，第五只为坏或前四只三好一坏第五只为好∴ ∴ 分布列为2345P三、条件概率、事件的独立性、独立重复试验、二项分布与超几何分布1、条件概率：称为在事件A发生的条件下，事件B发生的概率。

2、相互独立事件：如果事件A（或B）是否发生对事件B （或A）发生的概率没有影响，这样的两个事件叫做相互独立事件。

①如果事件A、B是相互独立事件，那么，A与、与B、与都是相互独立事件②两个相互独立事件同时发生的概率，等于每个事件发生的概率的积。

我们把两个事件A、B同时发生记作AB，则有P（AB）= P（A）P（B）推广：如果事件A1，A2，…An相互独立，那么这n个事件同时发生的概率，等于每个事件发生的概率的积。

概率论与数理统计练习题系第二章专业班姓名随机变量及其分布（一）学号一．选择题：1 ．设X是失散型随机变量，以下可以作为X的概率分布是[B]X x1x2x3x4X x1x2x3x4（ A）1111（B）1111 p p248162488X x1x2x3x4（D）X x1x2x3x4（ C）1111p1111 p23412234122 ．设随机变量ξ的分布列为X0123C ] p0.10.30.4F ( x) 为其分布函数，则 F ( 2) = [0.2（ A）（B）（ C）（D）1二、填空题：1 ．设随机变量X的概率分布为X012，则 a = p a0.20.52 ．某产品 15 件，其中有次品 2 件。

现从中任取3 件，则抽得次品数X 的概率分布为P(X 0)C13366， P( x1)C21 C13236， P( xC22 C1313 C153105C1531052)105C1533 ．设射手每次击中目标的概率为, 连续射击10 次，则击中目标次数X 的概率分布为P( X k ) C10k(0.7)k (0.3)10 k(k0,1, 2,L ,10)三、计算题：1 ．同时掷两颗骰子，设随机变量X为“两颗骰子点数之和”求：（ 1）X的概率分布；（2）P( X3) ；（3）P( X12)解：（1）P( X2)1P( X3)2P( X4)3P(X 5)4，，，，36363636P( X6)5，P( X7) 6 ， P( X5 436 8)， P(X 9)363636P( X10)3 ，P( X11)2 ，P( X 1363612)36所以 X 的概率分布列：X 2 34 5 6 7 89 10 11 12P12 34 5 6 5 4 3 2 1363636363636 3636363636（2） P(X3) 336（ 3） P(X>12)=02 ．产品有一、 二、三等品及废品四种， 其中一、 二、三等品及废品率分别为 60%，10%，20%及 10%，任取一个产品检查其质量，试用随机变量X 描述检查结果。

第二章 《随机变量及其分布》练习题一、选择题1．任意抛掷三枚均匀硬币，恰有2枚正面朝上的概率为( )A ．34 B ．38 C ．13 D ．142．在4次独立重复试验中，事件A 发生的概率相同，若事件A 至少发生1次的概率为6581，则事件A 在1次试验中发生的概率为( )A ．13 B ．25 C ．56 D ．343．若X ～B (10,0.8)，则P (X ＝8)等于( )A ．C 810×0.88×0.22B ．C 810×0.82×0.28 C ．0.88×0.22D ．0.82×0.284．若X 是一个随机变量，则E (X －E (X ))的值为( )A ．无法求B ．0C ．E (X )D ．2E (X )5．某人从家乘车到单位，途中有3个交通岗．假设在各交通岗遇到红灯的事件是相互独立的，且概率都是0.4，则此人上班途中遇红灯次数的均值为( ) A ．0.4 B ．1.2 C ．0.43D ．0.66．已知随机变量ξ的概率分布如下表所示：且η＝2ξ＋3，则E (η)等于( )A.35 B.65 C.215 D.1257．随机变量ξ的分布列为则ξ的数学期望是( )A ．2B ．2.1C ．2.3D ．随m 的变化而变化8．某班有14的学生数学成绩优秀，如果从班中随机地找出5名学生，那么其中数学成绩优秀的学生数ξ～B ⎝⎛⎭⎫5，14，则E (－ξ)的值为( ) A.14 B ．－14 C.54 D ．－549．有10张卡片，其中8张标有数字2,2张标有数字5，从中任意抽出3张卡片，设3张卡片上的数字之和为X ，则X 的数学期望是( )A ．7.8 B ．8 C ．16 D ．15.6 10．设随机变量ξ的分布列如下表：且E (ξ)＝1.6，则a －b 等于( D ．－0.411．设一随机试验的结果只有A 和A 且P (A )＝m ，令随机变量ξ＝⎩⎪⎨⎪⎧1，A 发生0，A 不发生，则ξ的方差D (ξ)等于( )A ．mB ．2m (1－m )C ．m (m －1)D ．m (1－m )12．由以往的统计资料表明，甲、乙两运动员在比赛中得分情况为：D ．无法确定 13．已知随机变量ξ，η满足ξ＋η＝8，且ξ服从二项分布ξ～B (10,0.6)，则E (η)和D (η)的值分别是( )A ．6和2.4B ．2和2.4C ．2和5.6D ．6和5.614.随机变量X 的分布列如下：若E (X )＝158，则D (X )等于( ) A.732 B.932 C.3364 D.556415．若随机变量ξ的分布列为P (ξ＝m )＝13，P (ξ＝n )＝a ，若E (ξ)＝2，则D (ξ)的最小值等于( )A ．0B ．2C ．4D ．无法计算16．某班举行了一次“心有灵犀”的活动，教师把一张写有成语的纸条出示给A 组的某个同学，这个同学再用身体语言把成语的意思传递给本组其他同学．若小组内同学甲猜对成语的概率是0.4，同学乙猜对成语的概率是0.5，且规定猜对得1分，猜不对得0分，则这两个同学各猜1次，得分之和X (单位：分)的数学期望为( )A ．0.9 B ．0.8 C ．1.2 D ．1.117.有10张卡片，其中8张标有数字2,2张标有数字5，从中任意抽出3张卡片，设3张卡片上的数字之和为X ，则X 的数学期望是( )A ．7.8 B ．8 C ．16 D ．15.6二、填空题1．一射手对靶射击，直到第一次命中为止，每次命中的概率为0.6，现有4颗子弹，命中后的剩余子弹数目X 的期望为________．2．袋中装有6个红球，4个白球，从中任取1个球，记下颜色后再放回，连续摸取4次，设X 是取得红球的次数，则E (X )＝________.3．随机变量ξ的取值为0,1,2.若P (ξ＝0)＝15，E (ξ)＝1，则D (ξ)＝________.4.节日期间，某种鲜花的进价是每束2.5元，售价是每束5元，节后对没有卖出的鲜花以每束1.6元处理．根据前5年节日期间对这种鲜花需求量ξ(束)的统计(如下表)，若进这种鲜花500束在今年节日期间销售，则利润的均值是________元.三、解答题1．某师范大学志愿者支教团体有6名男同学，4名女同学．在这10名同学中，3名同学来自数学系，其余7名同学来自物理、化学等其他互不相同的七个系．现从这10名同学中随机选取3名同学，到希望小学进行支教活动（每位同学被选到的可能性相同）． （Ⅰ）求选出的3名同学来自互不相同的系的概率；（Ⅱ）设X 为选出的3名同学中女同学的人数，求随机变量X 的分布列和数学期望．2.现有甲、乙两个靶，某射手向甲靶射击一次，命中的概率为34；向乙靶射击一次命中的概率为23，该射手每次射击的结果相互独立．假设该射手进行一次测试，先向甲靶射击两次，若两次都命中，则通过测试；若两次中只命中一次，则再向乙靶射击一次，命中也可通过测试，其它情况均不能通过测试．(1)求该射手通过测试的概率；(2)求该射手在这次测试中命中的次数X 的分布列及数学期望．3．在“出彩中国人”的一期比赛中，有6位歌手(1～6)登台演出，由现场的百家大众媒体投票选出最受欢迎的出彩之星，各家媒体独立地在投票器上选出3位出彩候选人，其中媒体甲是1号歌手的歌迷，他必选1号，另在2号至6号中随机的选2名；媒体乙不欣赏2号歌手，他必不选2号；媒体丙对6位歌手的演唱没有偏爱，因此在1至6号歌手中随机的选出3名．(1)求媒体甲选中3号且媒体乙未选中3号歌手的概率；(2)用X表示3号歌手得到媒体甲、乙、丙的票数之和，求X的分布列及数学期望．4.某学校举行知识竞赛，第一轮选拔共设有A、B、C、D四个问题，规则如下：①每位参加者计分器的初始分均为10分，答对问题A、B、C、D分别加1分、2分、3分、6分，答错任一题减2分；②每回答一题，计分器显示累计分数，当累计分数小于8分时，答题结束，淘汰出局；当累计分数大于或等于14分时，答题结束，进入下一轮；当答完四题，累计分数仍不足14分时，答题结束，淘汰出局；③每位参加者按问题A、B、C、D顺序作答，直至答题结束．假设甲同学对问题A、B、C、D回答正确的概率依次为34、12、13、14，且各题回答正确与否相互之间没有影响．(1)求甲同学能进入下一轮的概率；(2)用ξ表示甲同学本轮答题结束时答题的个数，求ξ的分布列和数学期望E(ξ)．第二章 《随机变量及其分布》练习题一、选择题1．任意抛掷三枚均匀硬币，恰有2枚正面朝上的概率为( )A ．34 B ．38 C ．13 D ．14[解析] 抛一枚硬币，正面朝上的概率为12，则抛三枚硬币，恰有2枚朝上的概率为P ＝C 23⎝⎛⎭⎫122×12＝38. 2．在4次独立重复试验中，事件A 发生的概率相同，若事件A 至少发生1次的概率为6581，则事件A 在1次试验中发生的概率为( )A ．13 B ．25 C ．56 D ．34[解析] 事件A 在一次试验中发生的概率为p ，由题意得1－C 04p 0(1－p )4＝6581，所以1－p ＝23，p ＝13， 3．若X ～B (10,0.8)，则P (X ＝8)等于( )A ．C 810×0.88×0.22B ．C 810×0.82×0.28 C ．0.88×0.22D ．0.82×0.28[解析] ∵X ～B (10,0.8)，∴P (X ＝k )＝C k 100.8k (1－0.8)10－k ，∴P (X ＝8)＝C 8100.88·0.22，故选A ． 4．若X 是一个随机变量，则E (X －E (X ))的值为( )A ．无法求B ．0C ．E (X )D ．2E (X )[解析] 只要认识到E (X )是一个常数，则可直接运用均值的性质求解．∵E (aX ＋b )＝aE (X )＋b ，而E (X )为常数，∴E (X －E (X ))＝E (X )－E (X )＝0. [答案] B5．某人从家乘车到单位，途中有3个交通岗．假设在各交通岗遇到红灯的事件是相互独立的，且概率都是0.4，则此人上班途中遇红灯次数的均值为( )A ．0.4B ．1.2C ．0.43D ．0.6[解析] ∵途中遇红灯的次数X 服从二项分布，即X ～B (3,0.4)，∴E (X )＝3×0.4＝1.2. [答案] B 6．已知随机变量ξ的概率分布如下表所示：且η＝2ξ＋3，则E (η)等于( )A.35 B.65 C.215 D.125解析：E (ξ)＝0×715＋1×715＋2×115＝35，E (η)＝E (2ξ＋3)＝2E (ξ)＋3＝2×35＋3＝215.答案：C7．随机变量ξ的分布列为则ξ的数学期望是( )A ．2B ．2.1C ．2.3D ．随m 的变化而变化解析：∵0.2＋0.5＋m ＝1，∴m ＝0.3，∴E (ξ)＝1×0.2＋2×0.5＋3×0.3＝2.1.答案：B8．某班有14的学生数学成绩优秀，如果从班中随机地找出5名学生，那么其中数学成绩优秀的学生数ξ～B ⎝⎛⎭⎫5，14，则E (－ξ)的值为( )A.14 B ．－14 C.54 D ．－54 解析：∵E (ξ)＝5×14＝54，∴E (－ξ)＝－E (ξ)＝－54，故选D.9．有10张卡片，其中8张标有数字2,2张标有数字5，从中任意抽出3张卡片，设3张卡片上的数字之和为X ，则X 的数学期望是( )A ．7.8 B ．8 C ．16 D ．15.6解析：X 的取值为6,9,12，P (X ＝6)＝C 38C 310＝715，P (X ＝9)＝C 28C 12C 310＝715，P (X ＝12)＝C 18C 22C 310＝115.E (X )＝6×715＋9×715＋12×115＝7.8.答案：A10．设随机变量ξ的分布列如下表：且E (ξ)＝1.6，则a －b 等于( D ．－0.4解析：根据题意，⎩⎪⎨⎪⎧ 0.1＋a ＋b ＋0.1＝1，0×0.1＋a ＋2×b ＋3×0.1＝1.6，解得⎩⎪⎨⎪⎧a ＝0.3b ＝0.5.所以a －b ＝－0.2.答案C11．设一随机试验的结果只有A 和A 且P (A )＝m ，令随机变量ξ＝⎩⎪⎨⎪⎧1，A 发生0，A 不发生，则ξ的方差D (ξ)等于( )A ．mB ．2m (1－m )C ．m (m －1)D ．m (1－m ) 解析：依题意ξ服从两点分布，∴D (ξ)＝m (1－m )，故选D.12．由以往的统计资料表明，甲、乙两运动员在比赛中得分情况为：A ．甲B ．乙C ．甲、乙均可D ．无法确定解析：E (ξ1)＝E (ξ2)＝1.1，D (ξ1)＝1.12×0.2＋0.12×0.5＋0.92×0.3＝0.49，D (ξ2)＝1.12×0.3＋0.12×0.3＋0.92×0.4＝0.69，∴D (ξ1)<D (ξ2)，即甲比乙得分稳定，选甲参加较好，故选A.13．已知随机变量ξ，η满足ξ＋η＝8，且ξ服从二项分布ξ～B (10,0.6)，则E (η)和D (η)的值分别是( )A ．6和2.4 B ．2和2.4 C ．2和5.6D ．6和5.6解析：由已知E (ξ)＝10×0.6＝6，D (ξ)＝10×0.6×0.4＝2.4.∵ξ＋η＝8，∴η＝8－ξ.∴E (η)＝－E (ξ)＋8＝2，D (ξ)＝(－1)2D (ξ)＝2.4.答案：B 14.随机变量X 的分布列如下：若E (X )＝158，则D (X )等于( ) A.732 B.932 C.3364 D.5564解析：由⎩⎪⎨⎪⎧1×0.5＋2x ＋3y ＝158，0.5＋x ＋y ＝1，得⎩⎨⎧x ＝18，y ＝38.所以D (X )＝⎝⎛⎭⎫1－1582×12＋⎝⎛⎭⎫2－1582×18＋⎝⎛⎭⎫3－1582×38＝5564. 答案：D15．若随机变量ξ的分布列为P (ξ＝m )＝13，P (ξ＝n )＝a ，若E (ξ)＝2，则D (ξ)的最小值等于( )A ．0B ．2C ．4D ．无法计算解析：由于分布列中，概率和为1，则a ＋13＝1，a ＝23. ∵E (ξ)＝2，∴m 3＋2n3＝2.∴m ＝6－2n .∴D (ξ)＝13×(m －2)2＋23×(n －2)2＝23×(n －2)2＋13×(6－2n －2)2＝2n 2－8n ＋8＝2(n －2)2.∴n ＝2时，D (ξ)取最小值0.答案：A16．某班举行了一次“心有灵犀”的活动，教师把一张写有成语的纸条出示给A 组的某个同学，这个同学再用身体语言把成语的意思传递给本组其他同学．若小组内同学甲猜对成语的概率是0.4，同学乙猜对成语的概率是0.5，且规定猜对得1分，猜不对得0分，则这两个同学各猜1次，得分之和X (单位：分)的数学期望为( )A ．0.9 B ．0.8 C ．1.2D ．1.1[解析] X 的取值为0、1、2，P (X ＝0)＝(1－0.4)(1－0.5)＝0.3， P (X ＝1)＝0.4×(1－0.5)＋(1－0.4)×0.5＝0.5， P (X ＝2)＝0.4×0.5＝0.2，∴E (X )＝0×0.3＋1×0.5＋2×0.2＝0.9. [答案] A17.有10张卡片，其中8张标有数字2,2张标有数字5，从中任意抽出3张卡片，设3张卡片上的数字之和为X ，则X 的数学期望是( )A ．7.8 B ．8 C ．16 D ．15.6[解析] X 的取值为6、9、12，P (X ＝6)＝C 38C 310＝715，P (X ＝9)＝C 28C 12C 310＝715，P (X ＝12)＝C 18C 22C 310＝115. E (X )＝6×715＋9×715＋12×115＝7.8. [答案] A二、填空题1．一射手对靶射击，直到第一次命中为止，每次命中的概率为0.6，现有4颗子弹，命中后的剩余子弹数目X 的期望为________．解析：X 的可能取值为3,2,1,0，P (X ＝3)＝0.6；P (X ＝2)＝0.4×0.6＝0.24；P (X ＝1)＝0.42×0.6＝0.096；P (X ＝0)＝0.43＝0.064.所以E (X )＝3×0.6＋2×0.24＋1×0.096＋0×0.064＝2.376.2．袋中装有6个红球，4个白球，从中任取1个球，记下颜色后再放回，连续摸取4次，设X 是取得红球的次数，则E (X )＝________.解析：每一次摸得红球的概率为610＝35，由X ～B ⎝⎛⎭⎫4，35，则E (X )＝4×35＝125. 3．随机变量ξ的取值为0,1,2.若P (ξ＝0)＝15，E (ξ)＝1，则D (ξ)＝________.解析：由题意设P (ξ＝1)＝p ，则ξ的分布列如下由E (ξ)＝1，可得p ＝35，所以D (ξ)＝12×15＋02×35＋12×15＝25. 答案：254.节日期间，某种鲜花的进价是每束2.5元，售价是每束5元，节后对没有卖出的鲜花以每束1.6元处理．根据前5年节日期间对这种鲜花需求量ξ(束)的统计(如下表)，若进这种鲜花500束在今年节日期间销售，则利润的均值是________元.解析：节日期间这种鲜花需求量的均值为E (ξ)＝200×0.20＋300×0.35＋400×0.30＋500×0.15＝340(束)．设利润为η，则η＝5ξ＋1.6×(500－ξ)－500×2.5＝3.4ξ－450， 所以E (η)＝3.4E (ξ)－450＝3.4×340－450＝706(元)． 三、解答题1．某师范大学志愿者支教团体有6名男同学，4名女同学．在这10名同学中，3名同学来自数学系，其余7名同学来自物理、化学等其他互不相同的七个系．现从这10名同学中随机选取3名同学，到希望小学进行支教活动（每位同学被选到的可能性相同）． （Ⅰ）求选出的3名同学来自互不相同的系的概率；（Ⅱ）设X 为选出的3名同学中女同学的人数，求随机变量X 的分布列和数学期望． 解：（Ⅰ）3A 设“选出的名同学来自互不相同的系”为事件，1203373731049()60C C C C P A C346310()(0,1,2,3)k k c c p xk k c （Ⅱ）随机变量X 的所有可能值为0，1，2，3.随机变量X 的分布列为数学期望113161236210305E X ．2.现有甲、乙两个靶，某射手向甲靶射击一次，命中的概率为34；向乙靶射击一次命中的概率为23，该射手每次射击的结果相互独立．假设该射手进行一次测试，先向甲靶射击两次，若两次都命中，则通过测试；若两次中只命中一次，则再向乙靶射击一次，命中也可通过测试，其它情况均不能通过测试．(1)求该射手通过测试的概率；(2)求该射手在这次测试中命中的次数X 的分布列及数学期望．[解析] (1)设“该射手通过测试”为事件A ，“向甲靶射击两次都命中”为事件B ，“向甲靶射击两次中只命中一次，则再向乙靶射击一次，命中”为事件C ．事件B ，C 互斥，且A ＝B ＋C ．所以该射手通过测试的概率P (A )＝P (B )＋P (C )＝⎝⎛⎭⎫342＋C 12·34·⎝⎛⎭⎫1－34·23＝1316. (2)由题意知，X ＝0,1,2. P (X ＝0)＝⎝⎛⎭⎫1－342＝116；P (X ＝1)＝C 12·34·⎝⎛⎭⎫1－34·⎝⎛⎭⎫1－23＝18；P (X ＝2)＝P (A )＝1316. 所以该射手在这次测试中命中的次数X 的分布列为该射手在这次测试中命中的次数X 的数学期望为E (X )＝0×116＋1×18＋2×1316＝74.3．在“出彩中国人”的一期比赛中，有6位歌手(1～6)登台演出，由现场的百家大众媒体投票选出最受欢迎的出彩之星，各家媒体独立地在投票器上选出3位出彩候选人，其中媒体甲是1号歌手的歌迷，他必选1号，另在2号至6号中随机的选2名；媒体乙不欣赏2号歌手，他必不选2号；媒体丙对6位歌手的演唱没有偏爱，因此在1至6号歌手中随机的选出3名．(1)求媒体甲选中3号且媒体乙未选中3号歌手的概率；(2)用X 表示3号歌手得到媒体甲、乙、丙的票数之和，求X 的分布列及数学期望．[分析] (1)设A 表示事件：“媒体甲选中3号歌手”，B 表示事件“媒体乙选中3号歌手”，C 表示事件“媒体丙选中3号歌手”，由等可能事件概率公式求出P (A )，P (B )，由此利用相互独立事件的概率乘法公式和对立事件的概率公式能求出媒体甲选中3号歌手且媒体乙未选中3号歌手的概率．(2)先由等可能事件概率计算公式求出P (C )，由已知得X 的可能取值为0,1,2,3，分别求出相应的概率，由此能求出X 的分布列及数学期望．[解析] (1)设A 表示事件“媒体甲选中3号歌手”，B 表示事件“媒体乙选中3号歌手”，C 表示事件“媒体丙选中3号歌手”， P (A )＝C 14C 25＝25，P (B )＝C 24C 35＝35，媒体甲选中3号且媒体乙未选中3号歌手的概率为P (A B )＝P (A )(1－P (B ))＝25×(1－35)＝425.(2)P (C )＝C 25C 36＝12，由已知得X 的可能取值为0,1,2,3，P (X ＝0)＝P (A B C )＝(1－25)(1－35)(1－12)＝325，P (X ＝1)＝P (A B C )＋P (A B C )＋P (A B C )＝25(1－35)(1－12)＋(1－25)×35×(1－12)＋(1－25)(1－35)×12＝1950， P (X ＝2)＝P (AB C )＋P (A B C )＋P (A BC )＝25×35×(1－12)＋25(1－35)×12＋(1－25)×35×12＝1950，P (X ＝3)＝P (ABC )＝25×35×12＝325，∴X 的分布列为E (X )＝0×325＋1×1950＋2×1950＋3×325＝32.114.某学校举行知识竞赛，第一轮选拔共设有A 、B 、C 、D 四个问题，规则如下：①每位参加者计分器的初始分均为10分，答对问题A 、B 、C 、D 分别加1分、2分、3分、6分，答错任一题减2分；②每回答一题，计分器显示累计分数，当累计分数小于8分时，答题结束，淘汰出局；当累计分数大于或等于14分时，答题结束，进入下一轮；当答完四题，累计分数仍不足14分时，答题结束，淘汰出局；③每位参加者按问题A 、B 、C 、D 顺序作答，直至答题结束．假设甲同学对问题A 、B 、C 、D 回答正确的概率依次为34、12、13、14，且各题回答正确与否相互之间没有影响．(1)求甲同学能进入下一轮的概率；(2)用ξ表示甲同学本轮答题结束时答题的个数，求ξ的分布列和数学期望E (ξ)．[解析] 设A 、B 、C 、D 分别表示甲同学能正确回答第一、二、三、四个问题的事件，A －、B －、C －、D－分别为A 、B 、C 、D 的对立事件(例如A －表示甲同学第一题回答错误)．由题设条件知，P (A )＝34，P (B )＝12，P (C )＝13，P (D )＝14，P (A －)＝14，P (B －)＝12，P (C －)＝23，P (D －)＝34. (1)记“甲同学能进入下一轮”为事件W ，则由题设条件知W ＝ABC ＋AB C －D ＋A B －CD ＋A －BCD ＋A－B C －D ，∵A 、B 、C 、D 各事件相互独立，∴P (W )＝P (A )·P (B )·P (C )＋P (A )·P (B )·P (C －)·P (D )＋P (A )·P (B －)·P (C )·P (D )＋P (A －)·P (B )·P (C )·P (D )＋P (A －)·P (B )·P (C －)·P (D )＝34×12×13＋34×12×23×14＋34×12×13×14＋14×12×13×14＋14×12×23×14＝14. (2)由题意知，ξ的可能取值为2、3、4，则P (ξ＝2)＝P (A －B －)＝P (A －)·P (B －)＝14×12＝18， P (ξ＝3)＝P (ABC ＋A B －C －)＝P (A )P (B )P (C )＋P (A )P (B －)P (C －)＝34×12×13＋34×12×23＝38. P (ξ＝4)＝1－P (ξ＝2)－P (ξ＝3)＝1－18－38＝12， ∴ξ的分布列为∴E (ξ)＝2×18＋3×38＋4×12＝278.。

随机变量及其概率分布练习题(共90分)一．选择题(每题2分共20分)2．F(X)是随机变量X 的分布函数，则下列结论不正确的是（ ）A.≤0F(x )1≤B.F(x )=P{X=x }C.F(x )=P{X x ≤}D.F(∞+)=1, F(∞-)=03．设随机变量X 的分布律为如下表格：F(x)为其分布函数，则F(5)=( ) X0 2 4 6 P 0.1 0.2 0.3 0.4A.0.3B.0.5C.0.6D.0.44．下列函数可以作为随机变量分布函数的是（ ） 4x 01≤≤x 2x 10<≤xA.F(x)=B.F(x)=1 其它2 其它-1 x<0 0 x<0C.F(x)= 2x 10<≤xD.F(x)= 2x 5.00<≤x 1 其它 1 x ≥0.54x 31<<-x 5．设X 的密度函数为f(x)= 则P{-2<x<2}=( ) 0, 其它A. 0B.83C. 43D. 856. 以下函数可作为随机变量X 的概率密度的是（ ）A.f(x)=.;11,0,其它<<-⎩⎨⎧x xB.f(x)=.;11,,02其它<<-⎩⎨⎧x xC.f(x)=.;11,0,21其它<<-⎪⎩⎪⎨⎧x D.f(x)=.;11,0,2其它<<-⎩⎨⎧x7.设随机变量X~N(1，4)，5.0)0(,8413.0)1(=Φ=Φ，则事件{13X ≤≤}的概率为（） A.0.1385 B.0.2413 C.0.2934 D.0.34138．已知随机变量X 的分布函数为（ ）F(x)= ⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧≥<≤<≤<313132102100x x x x ，则P }{1X ==A ． 61B ．21C ．32D ．19．已知连续型随机变量X 服从区间[a ，b ]上的均匀分布，则概率=⎭⎬⎫⎩⎨⎧+<32b a X P ( )A ．0B ．31C ．32D ．110、设随机变量X 在区间[2，6]上服从均匀分布，则P{2<x<4}=( )A.P{5<x<7}B.p{1<x<3}C.P{3<x<5}D.P{4.5<x<6.5}二．填空题(每题2分共20分)2．设连续型随机变量X 的分布函数为如下F(x), 则X 的概率密度)(x f 为（ ） 0 x<0F(x)= 2x, 5.00<≤x1 x ≥0.53．设随机变量X 的分布为P{X=k}=10k，k=0,1，2,3,4,则P{0.5<X ≤2}=( )4．设随机变量X ～N(2,9)，已知标准正态分布函数值=Φ)1(0.8413，为使P{X<a}<0.8413,则常数a<( )5．某人掷五次骰子，则在五次中得到点为6的次数X 的分布率为P{X=i}=( ) i=0,1,2,3,4,56．设随机变量X 服从区间[]10,0上的均匀分布，则P （X>4）=_ _．7．在[]T ,0内通过某交通路口的汽车数X 服从泊松分布，且已知P{X=4}=3P{X=3}，则在[]T ,0内至少有一辆汽车通过的概率为_ _．8.已知随机变量X 的分布函数为F(x)=⎪⎪⎪⎩⎪⎪⎪⎨⎧≥<≤<≤<3x 13x 1321x 0210x 0 则P{2<X ≤4}=_ _．9.已知随机变量X 的概率密度为f(x)=ce -|x|，-∞<x<+∞，则c=_ _．10．设随机变量X 的概率分布为F (x )为其分布函数，则F (3)=_ _．三．计算题。

第二章 随机变量及其分布第一节 随机变量、离散型随机变量及其分布规律一、判断题 随机变量X 的分布规律1． 表 是变量X 有{}3,2,1,0,652=−==k k k X P ，则它2.若对随机是随机变量X 的分布规律3.若对随机变量X 有{},5,4,3,2,1,251=+==k k k X P 则它是随机变量X 的分布律 二、填空题1.设随机变量X 的分布律为{}N k Nak X P ⋯⋯===,4,3,2,1,,则=a 2.设随机变量X 的分布律为{}⋯⋯===−,2,1,!3k e k k X P kλ，则=λ3.设离散型随机变量X 服从两点分布，且()()()=====1,041X P X P X P 则4.设随机变量(),,~p n b X 且已知()()(),3221=====X P X P X P 则n = p =5.某试验的成功概率为43，失败概率为41，若以X 表示试验者首次成功所进行的试验次数，则X 的分布律为6.设随机变量X 服从二项分布(),,2p b 随机变量Y 服从二项分布若()p b ,3。

若(),951=≥X P 则()=≥1Y P三、在15件同类型的零件中有2件次品，从中取3次，每次任取1件，作不放回抽取。

以X 表示取出的次品的个数。

1．求X 的分布律 2.画出分布律的图形四、一大楼装有5个同类型的供水设备。

调查表明在任一时刻t 每个设备被使用的概率为0.1，问在同一时刻, 1.恰有2个设备被使用的概率是多少？2.至少有3个设备被同时使用的概率是多少？3.至多有3个设备被同时使用的概率是多少？五、设某城市在一周内发生交通事故的次数服从参数为0.3的泊松分布，试问： 1.在一周内恰好发生2次交通事故的概率是多少？ 2.在一周内至少发生1次交通事故的概率是多少？六、某商店过去的销售记录表明，某种商品每月的销售数可用参数10=λ的泊松分布描述，为了以99%以上的把握该种商品不脱销，每月该种产品的库存量为多少件？七、设X 服从泊松分布，其分布律为{}⋯===−,1,0,!k k e k X P k λλ ,当k 为何值，()k X P =最大？第二节 随机变量分布函数、连续型随机变量及其概率密度一、判断题：1.(),.102,212,0⎪⎩⎪⎨⎧≥<≤−−<=x x x x F 是某个随机变量的分布函数。

随机变量及其分布练习试卷1(题后含答案及解析) 题型有：1. 单项选择题 2. 多项选择题 3. 综合分析题单项选择题每题1分。

每题的备选项中，只有1个符合题意。

1．一个样本由n个观测值组成，已知样本均值的样本标准差S皆为正数，如果每个观测值扩大到2倍，则下列说法正确的是()。

A．和S都扩大2倍B．和S都不变C．扩大2倍，S扩大4倍D．扩大4倍，S扩大2倍正确答案：C解析：由E(aX+b)＝aE(X)+b var(ax+b)＝a2var(X)可知。

知识模块：随机变量及其分布2．以下分别用来表示分布的中心位置和散布的大小的特征值是()。

A．均值、方差B．方差、均值C．标准差、均值D．方差、标准差正确答案：A解析：均值表示了分布的中心位置，方差和标准差表示分布的散布的大小。

知识模块：随机变量及其分布设随机变量Z的分布列为：X：0 1 2 3 4 P：0.50.20.10.15 0.05则3．E(X)为()。

A．0.105B．2.0C．1.6D．1.0正确答案：A解析：(1)E(X)=0×0.5+1×0.2+2×0.1+3×0.15+4×0.05＝0.105知识模块：随机变量及其分布4．P(0≤X＜3)为()。

A．0.9C．0.4D．0.7正确答案：B解析：(2)P(0≤X＜3)＝0.5+0.2+0.1＝0.8知识模块：随机变量及其分布5．设X为[a、b)上的连续型随机变量，已知a＜c＜d＜b，且c-a＝d-c＝b-d，则下列结论成立的是()。

A．P(a＜X≤d)＝2P(a＜X≤c)B．P(c＜X≤d)＝P(d＜X≤b)C．P(a≤X＜b)＝1/3D．P(X＝a)＝P(X＝b)正确答案：D解析：对于连续型随机变量，在给定区间上取值的概率P是以在取值区间上，概率密度分布曲线与X轴所夹的曲边梯形的面积。

对于连续随机变量X取一点的概率为0，所以选D。

知识模块：随机变量及其分布6．设X～N(1，4)，则P(0≤X＜2)可表示为()。

随机变量及其分布期末练习题及答案1．在事件A 发生的概率为p 的伯努利试验中，若以ξ记第r 次A 发生时的试验的次数，求ξ的分布。

[解] {}发生次试验次而第恰好出现了次试验中前A k r A k P k P 11-)(-==ξ),1,(,)1()1(11111 +=-=⋅-=-------r r k p p Cp p pC rk r r k r k r r k小结 求离散型随机变量的分布律时，首先应该搞清随机变量取可能值时所表示的随机事件，然后确定其分布列。

为验证所求分布是否正确，通常可计算一下所求得的“分布列”之和是否为1，若不是，则结果一定是错误的。

2．设随机变量X 的分布函数为⎪⎩⎪⎨⎧>≤≤<=.1,1;10.0,1)(2x x Ax x x F求（1）A 的值；（2）X 落在)21,1(-及)2,31(内的概率；（3）X 的概率密度函数。

[解] （1）有分布函数的右连续性， 在1=x 点处有1)01()1(=+==F A F ，即1=A （2）由分布函数的性质知，41)1()21())21,1((=--=-∈F F X P ；98311)31()2())2,31((2=⎪⎭⎫⎝⎛-=-=-∈F F X P ；（3）由于)(x F 最多除1=x 和0点外处处可导，且在1,0=x 处连续，若取⎩⎨⎧≤≤><=.10,2;10,0)(x x x x x f 或则0)(≥x f ，且对一切x 有⎰∞-=xdt t f x F )()(，从而)(x f 为随机变量X 的密度函数。

3．设),2(~2σN X ，且3.0)42(=<<X P ，求)0(<X P [解] 因为 )0(2)42(3.0Φ-⎪⎭⎫⎝⎛Φ=<<=σX P 所以 8.05.03.02=+=⎪⎭⎫⎝⎛Φσ于是 2.0212202)0(=⎪⎭⎫⎝⎛Φ-=⎪⎭⎫ ⎝⎛-Φ=⎪⎭⎫⎝⎛-<-=<σσσσX P X P4．一批鸡蛋，优良品种占三分之二，一般品种占三分之一，优良品种蛋重（单位：克）)5,55(~21N X ，一般品种蛋重)5,45(~22N X 。

第二章 随机变量及其分布1、解：设公司赔付金额为X ，那么X 的可能值为； 投保一年因意外死亡：20万，概率为0.0002 投保一年因其他原因死亡：5万，概率为0.0010投保一年没有死亡：0，概率为1-0.0002-0.0010=0.9988 所以X 的分布律为：2、一袋中有5X 表示取出的三只球中的最大，写出随机变量X 的分布律解：X 可以取值3，4，5，分布律为1061)4,3,2,1,5()5(1031)3,2,1,4()4(1011)2,1,3()3(352435233522=⨯====⨯====⨯===C C P X P C C P X P C C P X P 中任取两球再在号一球为中任取两球再在号一球为号两球为号一球为也可列为下表 X ： 3，4，5P ：106,103,1013、设在15只同类型零件中有2只是次品，在其中取三次，每次任取一只，作不放回抽样，以X 表示取出次品的只数，〔1〕求X 的分布律，〔2〕画出分布律的图形。

解：任取三只，其中新含次品个数X 可能为0，1，2个。

3522)0(315313===C C X P 3512)1(31521312=⨯==C C C X P 351)2(31511322=⨯==C C C X P 再列为下表 X ： 0，1，2P ：351,3512,35224、进展重复独立实验，设每次成功的概率为p ，失败的概率为q =1－p (0<p <1) 〔1〕将实验进展到出现一次成功为止，以X 表示所需的试验次数，求X 的分布律。

〔此时称X 服从以p 为参数的几何分布。

〕〔2〕将实验进展到出现r 次成功为止，以Y 表示所需的试验次数，求Y 的分布律。

〔此时称Y 服从以r, p 为参数的巴斯卡分布。

〕〔3〕一篮球运发动的投篮命中率为45%，以X 表示他首次投中时累计已投篮的次数，写出X 的分布律，并计算X 取偶数的概率。

解：〔1〕P (X=k )=q k －1p k=1,2,……〔2〕Y=r+n={最后一次实验前r+n －1次有n 次失败，且最后一次成功},,2,1,0,)(111 ===+=-+--+n p q C p p q C n r Y P r n n n r r n n n r 其中 q=1－p ，或记r+n=k ，那么 P {Y=k }= ,1,,)1(11+=----r r k p p C rk r r k 〔3〕P (X=k ) = (0.55)k －10.45 k=1,2…P (X 取偶数)=311145.0)55.0()2(1121===∑∑∞=-∞=k k k k X P 5、 一房间有3扇同样大小的窗子，其中只有一扇是翻开的。