第四讲 单纯型表格算法(运筹学-清华大学,林谦)
- 格式:ppt
- 大小:384.50 KB
- 文档页数:37


单纯形表法详细讲解
单纯形法是一种求解线性规划问题的数学方法。
以下是其详细步骤:
1. 确定初始基可行解:一般采用取松弛变量的方法来获得初始基可行解,从而得到对应的单位矩阵作为基。
2. 判断是否满足最优解条件:单纯形法从可行域中的一个点开始,判断该顶点是否为最优解。
如果不是,就寻找另一个目标函数值更优的顶点。
3. 迭代优化:通过单纯形表判断出顶点是否为最优解,如果线性规划问题没有最优解,则继续迭代优化,直到找到最优解或确定问题无解。
4. 确定最优解:在单纯形表中,理解其系数矩阵、基、基向量、非基向量和基变量等基本概念,从而确定最优解。
5. 确定换入变量和换出变量:在单纯形表中,如果发现非基变量的系数大于零,则可以通过增加这些变量的值来使目标函数增加。
由于每个变量都大于零,对于某个变量增加是有所限制的,如果该变量过大,由于其他限制条件,会导致其他变量小于零。
因此,应该让该变量一直增大,直到有一个其他变量刚好等于0为止,那么这个变量就被换出基。
6. 进行高斯行变换:使用第4行对各行进行高斯行变换,使得二列第四行中的每个x都变成零,也包括c2。
如需更多关于单纯形法的信息,可以咨询数学专家或查阅相关文献资料。

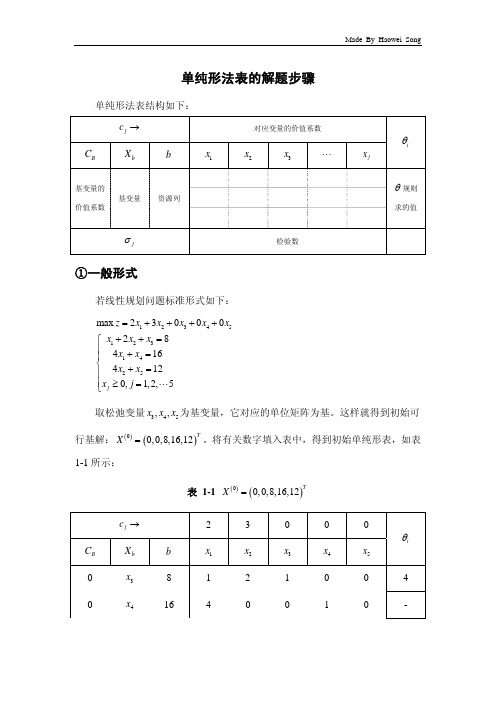
单纯形法表的解题步骤单纯形法表结构如下:j c →对应变量的价值系数i θB Cb Xb1x 2x 3x " j x基变量的价值系数基变量 资源列θ规则求的值j σ检验数①一般形式若线性规划问题标准形式如下:123451231425max 23000284164120,1,2,5j z x x x x x x x x x x x x x j =++++++=⎧⎪+=⎪⎨+=⎪⎪≥=⎩"取松弛变量345,,x x x 为基变量,它对应的单位矩阵为基。
这样就得到初始可行基解:()()00,0,8,16,12TX =。
将有关数字填入表中,得到初始单纯形表,如表1-1所示:表 1-1 ()()00,0,8,16,12TX =j c →2 3 0 0 0i θB C b X b1x 2x 3x 4x 5x0 3x 8 1 2 1 0 0 4 04x16 4 0 0 1 0 -5x12 0 [4] 0 0 1 3j σ2 3 0 0 0若检验数均未达到小于等于0,则对上表进行调整。
选择上表中检验数最大的列,该列对应的非变量为入基变量;再应用θ规则该列对应的各基变量对应的θ值,选出其中最小的一行,该行对应的基变量为出基变量。
修改单纯形表,对各行进行初等变换,确保基变量组成的矩阵为单为矩阵。
修改后的单纯形表如表1-2所示:表 1-2 ()()10,3,2,16,0TX =检验数12,0σσ>,则进行继续调整,调整后的单纯形法表如表1-3所示:表 1-3 ()()22,3,0,8,0TX =表1-3中, 50σ>,则继续进行调整,调整结果如表1-4所示:表 1-4 ()()34,2,0,0,4TX =检验数0j σ≤,这表示目标函数值已不可能再增大,于是得到最优解:()()3*4,2,0,0,4TX X ==*14z =②带人工变量现有线性规划问题:12312312313123min 321142321,,0z x x x x x x x x x x x x x x =−++−+≤⎧⎪−++≥⎪⎨−+=⎪⎪≥⎩ 将上述线性规划问题用大M 法求解,在约束条件中加入松弛变量4x ,剩余变量5x ,人工变量6x ,7x 得到:1234567123412356137min 300211423210,1,2,,7j z x x x x x Mx Mx x x x x x x x x x x x x x j =−++++++−++=⎧⎪−++−+=⎪⎨−++=⎪⎪≥=⎩"其中,M 是一个任意大的正数。

单纯形表法
单纯形表法是一种线性规划求解方法,通过转化为标准型后,利用单纯形法迭代寻找最优解。
单纯形表法的核心思想是不断的调整基变量,使目标函数值不断优化,直至找到最优解。
单纯形表法求解线性规划的过程中,需要建立一个单纯形表。
这个表由两部分组成,一部分是系数矩阵,另一部分是常数向量以及目标函数系数。
每一次迭代都会根据当前的基变量计算出对应的基变量的解,然后根据这些解更新单纯形表。
具体来说,就是将单纯形表中的非基变量全部设置为0,然后计算出每个基变量的值,以此更新单纯形表中的每一行,使其符合约束条件和目标函数的要求。
单纯形表法的优点在于可以求解大规模的线性规划问题,并且算法的时间复杂度较低。
但是,单纯形表法也存在一些缺点。
例如,可能会遇到无解的情况,或者算法会陷入循环中,并且在某些情况下,单纯形表法的迭代次数可能非常多,导致算法的效率降低。
在实际应用中,单纯形表法通常与其他线性规划求解方法结合使用,以达到更好的效果。
例如,可以使用单纯形表法进行初步求解,然后再使用其他优化算法进行进一步的优化。
- 1 -。

运筹学单纯形表法详细步骤概述运筹学是一门研究最优决策问题的学科,它通过数学建模和优化方法,寻找最佳解决方案。
运筹学的单纯形表法是一种常用的线性规划求解方法,通过构造单纯形表,逐步迭代求解最优解。
本文将详细介绍运筹学单纯形表法的步骤和算法原理。
单纯形表法步骤单纯形表法的基本思想是通过构造单纯形表,逐步迭代优化目标函数的值,直到找到最优解。
第一步:标准化线性规划问题将线性规划问题转化为标准型,使得约束条件为等式形式,目标函数为最小化形式。
标准型的形式如下:Minimize C1x1+C2x2+⋯+C n x nSubject to A11x1+A12x2+⋯+A1n x n=b1A21x1+A22x2+⋯+A2n x n=b2…A m1x1+A m2x2+⋯+A mn x n=b mx1,x2,…,x n≥0第二步:构造初始单纯形表根据线性规划问题的标准型,构造初始单纯形表。
初始单纯形表由约束系数矩阵、目标系数向量、约束条件向量和松弛变量构成。
约束系数矩阵的形式为:A=[A11A12...A1n100 0A21A22...A2n010 0⋮⋮⋱⋮⋮⋮⋮⋱⋮A m1A m2...A mn000 (1)]目标系数向量的形式为:C=[C1C2…C n000…0]约束条件向量的形式为:B=[b1b2…b m]第三步:确定初始解和基变量根据初始单纯形表,确定初始解和基变量。
基变量是与单位矩阵的列向量对应的变量,它们的取值为约束条件向量的值。
第四步:计算单纯形表中的各项值根据初始解和基变量,计算单纯形表中的各项值。
包括各变量的价值系数、约束条件的值,以及各松弛变量的值。
第五步:检查最优解检查单纯形表中目标系数行是否存在负数。
如果存在负数,则继续迭代;如果都为非负数,则找到最优解。
第六步:确定入基变量在目标系数行中选择最小的负数,确定进入基变量。
第七步:计算离基变量根据进入基变量,计算离开基变量。
离开基变量是通过计算变量的约束条件值除以进入基变量的列中对应的非零元素,找到最小的非负数所在行,确定离开基变量。