当前位置：文档之家 › 运筹学课件ch5指派问题[全文]

运筹学课件ch5指派问题[全文]

  • 格式：doc
  • 大小：32.00 KB
  • 文档页数：19

下载文档原格式

  / 19

合集下载

运筹与决策PPT：运输问题和指派问题

运筹与决策PPT：运输问题和指派问题

+ 690x23 + 791x24 + 995x31 + 682x32 + 388x33 + 685x34
s.t.
工厂 1: 工厂 2: 工厂 3: 仓库 1: 仓库 2: 仓库 3: 仓库 4:
x11 + x12 + x13 + x14
x21 + x22 + x23 + x24
= 75 供
= 125 x31 + x32 + x33 + x34 = 100
运输问题的Excel求解模型－ 案例1
B
C
3 Unit Cost
4
5 Source
Bellingham
6 (Cannery)
Eugene
7
Albert Lea
8
9
10 Shipment Quantity
11 (Truckloads)
12 Source
Bellingham
13 (Cannery)
Eugene
问题：如何改进运输策略以降低成本？
案例1：P&T公司的配送问题
CANNERY1 Bellingham
最偏远的厂
CANNERY2 Eugene
WAREHOUSE 3 Rapid City
WAREHOUSE 2 Salt Lake City
WAREHOUSE 1 Sacramento
WAREHOUSE 4 Albuquerque
4、运输问题和指派问题
引例
案例1：P&T公司的配送问题
▪ 家族经营的小公司，加工蔬菜罐头并分销到各地：
– 三个食品厂，四个分销仓库

运筹学指派问题课件

运筹学指派问题课件

c
i 1 j 1
n
n
ij
xij
n xij 1 i 1 n st . xij 1 (i , j 1, 2, ..., n) j 1 x 1or 0 ij
运筹学教程
例1：某商业公司计划开5家新商店，商业公司决定由5家建筑 公司分别承建。已知建筑公司Ai(i=1,2…5)对新商店Bj(j=1…5) 的建筑费用报价Cij.问题：商业公司对5家建筑公司如何分配任 务，才能使总的建筑费用最少？ Cij Ai Bj
运筹学教程
指派问题解法：匈牙利解法 解法思想：
若从系数矩阵C的任何一行（列）各元素中分别减去 一个常数K（K可正可负）得到新矩阵C’,则以C’为系 数矩阵的指派问题与原问题有相同的解，但最优值 比原问题最优值小K。
匈牙利法条件： MIN、i=j 、Cij≥0
运筹学教程
匈牙利法的主要步骤： 步骤1：变换系数矩阵，使在各行各列都出现零元素。 （1）从矩阵C的每行元素减去该行的最小元素；
0 11 8 7 7 3 3 2 1 C ' 5 0 4 3 4 0
第二步 圈0 寻找不同行不同列的0元素，圈之。 所在行和列其它0元素划掉
0 0 0 0 0 3 0 11 8 第三步 打 无的行打，打行上0列打 ， 1 7 7 3 打列上行打，打行上0列打 ' 2 3 2 1 C 0 5 0 4 0 3 0 11 8 0 1 7 7 3 2 3 4 0 C ' 0 2 3 2 1 第四步 确定方案划线 0 0 5 0 4 没有打行上画一条横线； 0 2 3 4 0 有打列上画一条竖线；
15 120 15 12 0 14 100 14 100 8 7 0 0 8 7

运输问题与指派问题讲义(PPT 40页)

运输问题与指派问题讲义(PPT 40页)

§3 Transportation Network 运输问题的网 络表示
销地
供应量
产地
B1
B2
B3
B3
ai
A1
6
7
5
3
25
A2
8
4
2
7
10
A2
5
9
10
16
15
需求量 bj
13
21
9
7
Transportation Network 运输问题的网络表示
sources
运价
Destinations 需求地
Warehouses
Destinations目的地
Output from a cannery
Supply from a source运出量
Allocation to a warehouse
Demand at a destination需求量
Shipping cost per truckload from a Cost per unit distributed from a
Eugene
125 truckloads
Salt Lake City
Albert Lea
100 truckloads
Rapid City
Total
300 truckloads
Albuquerque
Total
总产量=总的需求量=300车，产销平衡
分配量Allocation 80 truckloads 65 truckloads 70 truckloads 85 truckloads 300 truckloads
运输模型
例1、某公司从两个产地A1、A2将物品运往三个销地B1、B2、B3，各产地的 产量、各销地的销量和各产地运往各销地每件物品的运费如下表所示，

运筹学 指派问题课件 PPT

运筹学 指派问题课件 PPT
产品1 产品2 产品3 产品4
效率表
工厂1 工厂2
58 75
69 50
180 150
260 230
工厂3 工厂4
65 82
70 55
170 200
250 280
2
返回总目录
例1 某公司拟将四种新产品配置到四个工厂生产，四 个工厂的单位产品成本（元/件）如下表所示。求最 优生产配置方案使得单位产品成本总和为最小。
15
返回总目录
第三步：用最少的直线覆盖所有0：
0 0 11 22 22 25 25 0 0 0 0 0 5 5 5 27 27 0 45 45 6 17 17 0 30 0 0 0 0 0 0 0 0 45 45 32 6 17 17 0 0 0 0 0 0 0 45 45
回到第三步，用最少的直线覆盖所有0。 此时最少直线数=4，表明矩阵中存在4个不同行不 同列的零元素，于是得到最优解。 第五步：找出4个独立的0元：
( 0 ) 30 0 32 6 17 17 0 ( 0) 0 0 0 ( 0 ) (0 ) 45 45 ( 0 ) 30 0 32 6 17 17 0 0 ( 0 ) 0 ( 0) 0 (0 ) 45 45
x14 x24 x34 x44
工厂2 x21 工厂3 x31 工厂4 x41
1 1 1 1
1
1
1
1
产品1 产品2 产品3 产品4
工厂1 工厂2 工厂3 工厂4 58 75 65 82 69 50 70 55 180 150 170 200 260 230 250
5280
返回总目录
数学模型 匈牙利算法 其他变异的指派问题

运输问题和指派问题_图文

运输问题和指派问题_图文


表4－1 各工厂到各销售点的单位产品运价（元/吨）
B1
B2
B3
B4 产量（吨）
A1
3
11
3
10
7
A2
1
9
2
8
4
A3
7
4
10
5
9
销量（吨） 3
6
5
6
3.2 运输问题数学模型和电子表格模型
（1）产销平衡运输问题的数学模型

具有m个产地Ai（i＝1,2,,m）和n个销地

Bj（j＝1,2,,n）的运输问题的数学模型为
运输问题是一种特殊的线性规划问题，一般采用“表上作 业法”求解运输问题，但Excel的“规划求解”还是采用 “单纯形法”来求解。
例4.1的电子表格模型
3.2 运输问题数学模型和电子表格模型
需要注意的是：运输问题有这样一个性质 （整数解性质），只要它的供应量和需求 量都是整数，任何有可行解的运输问题必 然有所有决策变量都是整数的最优解。因 此，没有必要加上所有变量都是整数的约 束条件。
工厂1 工厂2 工厂3 需求量
表4－7 产品生产的有关数据
产品1 41 40 37 20
单位成本（元）
产品2 27 29 30 30
产品3 28 － 27 30
产品4 24 23 21 40
生产能力
75 75 45
3.3 各种运输问题变形的建模
解：指定工厂生产产品 可以看作运输问题来求 解。本题中，工厂2不能 生产产品3，这样可以增 加约束条件x23＝0 ；并 且，总供应（ 75+75+45=195）>总需求 （20+30+30+40=120）。 其数学模型如下： 设xij为工厂i生产产 品j的数量

《指派问题》课件

《指派问题》课件

指派问题的扩展研究
多目标指派问题
应用场景：生产调度、资源 分配等

解决方法：线性规划、启发 式算法等
定义：指派问题在多个目标 下的扩展
挑战：如何在多个目标之间 找到最优解
动态指派问题
动态指派问题的定 义
动态指派问题的应 用场景
动态指派问题的求 解方法
动态指派问题的优 化策略
大规模指派问题
问题定义：大规模 指派问题是指在给 定一组任务和一组 资源，如何将任务 分配给资源，使得 总成本最小化或总 收益最大化。
混合算法
混合算法的概念： 将多种算法进行 组合，以获得更 好的优化效果
混合算法的优点： 能够充分利用各 种算法的优点， 提高优化效果
混合算法的应用： 在指派问题中， 混合算法可以结 合多种算法，如 遗传算法、模拟 退火算法等，以 提高优化效果
混合算法的挑战： 如何合理选择和 组合各种算法， 以获得最佳的优 化效果
应用场景：大规 模指派问题广泛 应用于物流、供 应链、生产调度 等领域。
研究方法：大规 模指派问题的研 究方法包括启发 式算法、遗传算 法、神经网络等。
挑战与展望：大规 模指派问题的挑战 在于如何设计高效 的算法，以及如何 解决大规模问题中 的优化问题。未来 的研究方向包括分 布式计算、并行计 算等。
禁忌搜索法：在搜索过程中引入禁忌表，避免重复搜索已搜索过的解
元启发式方法
基本概念：元启发式 方法，也称为元启发 式算法，是一种基于 启发式策略的优化方 法。
特点：元启发式方 法具有自适应性、 鲁棒性和易于实现 等特点。
应用：元启发式方法 在指派问题、路径规 划、调度等问题中都 有广泛的应用。
实例：遗传算法、模 拟退火算法、蚁群算 法等都是元启发式方 法的典型代表。

北邮运筹学ch5-5 指派问题

北邮运筹学ch5-5 指派问题

则
min w
cij xij
ij
与
max z c x 运筹学 北ij京i邮j 电大学 的最优解相同。
ij
§5.5 指派问题 Assignment Problem
Ch5 Integer Programming
2020/1/27
Page 9 of 12
【例】某人事部门拟招聘4人任职4项工作，对他们综合考评的 得分如下表（满分100分），如何安排工作使总分最多。
2020/1/27
Page 7 of 12
不平衡的指派问题
当人数m大于工作数n时，加上m－n项工作，例如
5 9 10
11 6
3

8 14 17

6
4
5

3 2 1
5 9 10 0 0
11 6 3 0 0
8 14 17 0 0

6
4
5 0 0
进入练习
The End of Chapter 5
运筹学 北京邮电大下学 一章：图与网络 Exit
Ch5 Integer Programming
2020/1/27
Page 8 of 12
求最大值的指派问题 匈牙利法的条件是：模型求最小值、效率cij≥0
设C=(cij)m×m 对应的模型是求最大值 max z

cij xij
ij
将其变换为求最小值
令
M

max i, j
cij
C (M cij )
§5.5 指派问题 Assignment Problem
Ch5 Integer Programming
2020/1/27

运筹学课件ch5指派问题[全文]

运筹学课件ch5指派问题[全文]

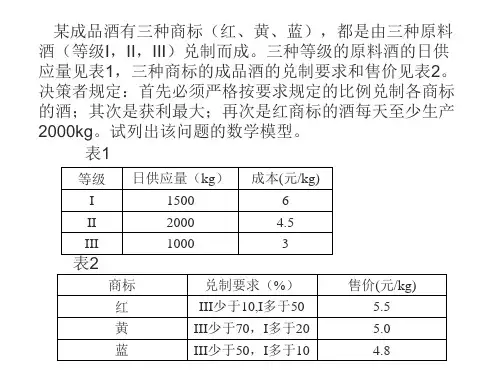
运筹学课件ch5指派问题[全文] 指派问题assignment problem 运筹学课件一种特殊的线性规划问题，我们也经常遇到指派人员做某项工作的情况。

指派问题的许多应用都用来帮助管理人员解决如何为一项将要开展进行的工作指派人员的问题。

其他的一些应用如为一项任务指派机器、设备或者是工厂。

指派问题运筹学课件指派问题的形式表述:给定了一系列所要完成的任务(tasks)以及一系列完成任务的被指派者(assignees)，所需要解决的问题就是要确定出哪一个人被指派进行哪一项任务。

指派问题模型运筹学课件指派问题的假设:被指派者的数量和任务的数量是相同的每一个被指派者只完成一项任务每一项任务只能由一个被指派者来完成每个被指派者和每项任务的组合有一个相关成本目标是要确定怎样进行指派才能使得总成本最小指派问题模型运筹学课件指派问题assignment problem 【例51></a>.14】人事部门欲安排四人到四个不同的岗位工作，每个岗位一个人(经考核四人在不同岗位的成绩(百分制)如表5-34所示，如何安排他们的工作使总成绩最好。

88809086丁90798382丙95788795乙90739285甲DCBA工作人员表5-34【解】设1 数学模型运筹学课件数学模型为:甲乙丙丁ABCD图5. 3指派问题assignment problem运筹学课件假设m个人恰好做m项工作，第i个人做第j项工作的效率为cij?0，效率矩阵为[cij](如表5-34)，如何分配工作使效率最佳(min或max)的数学模型为指派问题assignment problem运筹学课件2 解指派问题的匈牙利算法匈牙利法的条件是:问题求最小值、人数与工作数相等及效率非负【定理5.1】如果从分配问题效率矩阵[cij]的每一行元素中分别减去(或加上)一个常数ui(被称为该行的位势)，从每一列分别减去(或加上)一个常数vj(称为该列的位势)，得到一个新的效率矩阵[bij]，其中bij=cij,ui,vj,则[bij]的最优解等价于[cij]的最优解，这里cij、bij均非负(指派问题assignment problem【证】运筹学课件【定理5.2】若矩阵A的元素可分成“0”与非“0”两部分，则覆盖“0”元素的最少直线数等于位于不同行不同列的“0”元素(称为独立元素)的最大个数( 如果最少直线数等于m，则存在m个独立的“0”元素，令这些零元素对应的xij等于1，其余变量等于0，这时目标函数值等于零，得到最优解(两个目标函数相差一个常数 u+v,约束条件不变,因此最优解不变。

运筹学运输与指派问题 ppt课件

运筹学运输与指派问题 ppt课件
a1 a2
am
18
设xk（ =0或1）表示第k个中转站启用次数，xik表示从第i个仓库运到第k个中转站的 物资数量，ykj表示从第k个中转站运到第j个单位的物资数量，则
p
mp
pn
z f k x k
d ik x ik
e kj y kj
k 1
i1 k 1
k 1 j1
p
x ik a i
… … … …… …
Am cm1 cm2 … cmn am
Am+1 0
0 … 0 am+1
销量 b1 b2 … bn
mn
minz
cij xij
n
i1
xij ai
j1
i 1, 2,..., m
j1
s.t. m xij bj j 1, 2,..., n
i1
xij 0 i 1, 2,..., m; j 1, 2,..., n
mn
minz
cij xij
n
i1 j1
xij ai
i 1, 2,..., m
s.t.
j 1 m
xij
bj
j 1, 2,..., n
i1
xij 0 i 1, 2,..., m; j 1, 2,..., n
若用表上作业法求之,可设一个假想销地, 使其销
量为bn+1=∑ai-∑bj,ci,n+1=0.
已知该厂的生产能力与生产成本如下表。若生产出的产品当季不交货，则需
储存、维护等费用1500元。要求在完成合同的情况下，做出全年生产费用最
小的决策。
生产能力与生产成本
季度
1 2 3 4
生产的能力（台）

运筹学课件ch05资料

运筹学课件ch05资料

4
xi3 300, xi4 150
i1
i 1
4
4
s.t. x1 j 400, x2 j 600
i1
i 1
4
4
x3 j 200y. x4 j 200(1 y)
i1
i 1
xij 0(i, j 1,2,3,4), y 0或1
第1节 整数线性规划问题的提出
❖ 现举例说明用单纯形法求得的解不能保证是整数最优 解。
min
z
P1 (d1
d
2
d
3
d
4
d
5
d
6
)
P2
d
7
P3d8
x31
x11
0.1(x11 0.5(x11
x21 x21
x31) x31)
d1
d
2
d1
d
2
0 0
x32
0.7(x12
x22
x32
)
d
3
d3
0
x12
0.2(x12
x22
x32
)
d
4
d
4
0
x33
0.5(x13
解：这是物资运输问题，其特点是事先不能确定应该建A3或A4 中哪一个，因而不知道新厂投产后的实际生产费用。引入0—1
变量
1 y
0
若建工厂A3 若建工厂A4
44
min z
cij xij y1200 (1 y)1400
j1 i1
4
4
xi1 350, xi2 400
i1
i 1
4
解：每一个投资项目都有被选择和不被选择两种可能，为此令

第4章 运输问题和指派问题ppt课件

第4章 运输问题和指派问题ppt课件

x13
x 23
x 33
5
x14 x 24 x34 6
x
ij
0 (i
1, 2 , 3;
j
1,2,3,4 )
4.2 运输问题的数学模型和电子表格模型
运输问题是一种特殊的线性规划问题，一般采用“表上作
业法”求解运输问题，但Excel的“规划求解”还是采用
“单纯形法”来求解。
例4.1的电子表格模型
4.2 运输问题的数学模型和电子表格模型
需要注意的是，运输问题有这样一个性 质（整数解性质），即只要它的供应量 和需求量都是整数，任何有可行解的运 输问题就必然有所有决策变量都是整数 的最优解。因此，没有必要加上所有变 量都是整数的约束条件。
由于运输量经常以卡车、集装箱等为单 位，如果卡车不能装满，就很不经济了 。整数解性质避免了运输量（运输方案 ）为小数的麻烦。
i1
x
ij
0
(i 1, 2,
, m ; j 1, 2,
, n)
4.2 运输问题的数学模型和电子表格模型
（2）产大于销（供过于求）运输问题
的数学模型
（以满足小的销量为准）
m
n
ai bj
mn
m in z
cij xi j
i 1
j 1
i1 j 1
n
xij ai
Байду номын сангаас(i 1, 2,
,m)
m in
z 1 6 0 x A1 1 3 0 x A 2 2 2 0 x A3 1 7 0 x A4 1 4 0 xB1 1 3 0 xB 2 1 9 0 xB3 1 5 0 xB 4 190 xC1 200 xC 2 230 xC 3
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

运筹学课件ch5指派问题[全文] 指派问题assignment problem 运筹学课件一种特殊的线性规划问题，我们也经常遇到指派人员做某项工作的情况。

指派问题的许多应用都用来帮助管理人员解决如何为一项将要开展进行的工作指派人员的问题。

其他的一些应用如为一项任务指派机器、设备或者是工厂。

指派问题运筹学课件指派问题的形式表述:给定了一系列所要完成的任务(tasks)以及一系列完成任务的被指派者(assignees)，所需要解决的问题就是要确定出哪一个人被指派进行哪一项任务。

指派问题模型运筹学课件指派问题的假设:被指派者的数量和任务的数量是相同的每一个被指派者只完成一项任务每一项任务只能由一个被指派者来完成每个被指派者和每项任务的组合有一个相关成本目标是要确定怎样进行指派才能使得总成本最小指派问题模型运筹学课件指派问题assignment problem 【例51></a>.14】人事部门欲安排四人到四个不同的岗位工作，每个岗位一个人(经考核四人在不同岗位的成绩(百分制)如表5-34所示，如何安排他们的工作使总成绩最好。

88809086丁90798382丙95788795乙90739285甲DCBA工作人员表5-34【解】设1 数学模型运筹学课件数学模型为:甲乙丙丁ABCD图5. 3指派问题assignment problem运筹学课件假设m个人恰好做m项工作，第i个人做第j项工作的效率为cij?0，效率矩阵为[cij](如表5-34)，如何分配工作使效率最佳(min或max)的数学模型为指派问题assignment problem运筹学课件2 解指派问题的匈牙利算法匈牙利法的条件是:问题求最小值、人数与工作数相等及效率非负【定理5.1】如果从分配问题效率矩阵[cij]的每一行元素中分别减去(或加上)一个常数ui(被称为该行的位势)，从每一列分别减去(或加上)一个常数vj(称为该列的位势)，得到一个新的效率矩阵[bij]，其中bij=cij,ui,vj,则[bij]的最优解等价于[cij]的最优解，这里cij、bij均非负(指派问题assignment problem【证】运筹学课件【定理5.2】若矩阵A的元素可分成“0”与非“0”两部分，则覆盖“0”元素的最少直线数等于位于不同行不同列的“0”元素(称为独立元素)的最大个数( 如果最少直线数等于m，则存在m个独立的“0”元素，令这些零元素对应的xij等于1，其余变量等于0，这时目标函数值等于零，得到最优解(两个目标函数相差一个常数 u+v,约束条件不变,因此最优解不变。

指派问题assignment problem 运筹学课件匈牙利法由单纯形法衍生而来步骤(对min问题):建立成本表:必须为m*m方阵简化行:确定每一行最小值，并将该行的每个数字减去该最小值简化列:确定每一列最小值，并将该列的每个数字减去该最小值最佳性检验:使用最少的水平或垂直线覆盖所有0。

若线条数等于m，则停止，并进行最适当的指派;否则继续进一步简化成本表:在所有未被直线覆盖的数字中，确定其最小值所有未被直线覆盖的数字，减去该最小值所有同时被水平与垂直线画到的数字，加上该最小值返回步骤4 运筹学课件Which plants should produce which products?哪个工厂应该生产哪种产品,运筹学课件某汽车公司拟将四种新产品配置到四个工厂生产，四个工厂的单位产品成本(元/件)如表5-35所示(求最优生产配置方案( 2802005582工厂42501707065工厂32301505075工厂22601806958工厂1产品4产品3产品2产品1表5-35【解】问题求最小值。

第一步:找出效率矩阵每行的最小元素，并分别从每行中减去最小元素，有指派问题assignment problem运筹学课件第二步:找出矩阵每列的最小元素，再分别从每列中减去，有指派问题assignment problemMin 0 0 100 180 运筹学课件第三步:用最少的直线覆盖所有“0”，得第四步:这里直线数等于3(等于4时停止运算)，要进行下一轮计算(从矩阵未被直线覆盖的数字中找出一个最小数k并且减去k，矩阵中k,5( 直线相交处的元素加上k，被直线覆盖而没有相交的元素不变，得到下列矩阵指派问题assignment problem第四步等价于第1、3行减去5，同时第1列加上5得到的结果 -5-5+5运筹学课件第五步:覆盖所有零最少需要4条直线，表明矩阵中存在4个不同行不同列的零元素(容易看出4个“0”的位置( )××( )×( )( )或( )××( )×( )( )指派问题assignment problem运筹学课件得到两个最优解有两个最优方案第一种方案:第一个工厂加工产品1，第二工厂加工产品3，第三个工厂加工产品4，第四个工厂加工产品2;第二种方案:第一个工厂加工产品1，第二工厂加工产品4，第三个工厂加工产品3，第四个工厂加工产品2;单件产品总成本Z,58，150，250，55,513 指派问题assignment problem运筹学课件5.4.3 其它变异问题【例5.16】求例5.14的最优分配方案【解】则求此问题的最小值(求解过程如下最优分配方案是:甲分配到B岗位;乙分配到A岗位;丙分配到D岗位;丁分配到C岗位;总成绩为357指派问题assignment problem88809086丁90798382丙95788795乙90739285甲DCBA工作人员表5-34 运筹学课件丁的蛙泳成绩退步到1’15”2;戊的自由泳成绩进步到57”5, 组成接力队的方案是否应该调整,如何选拔队员组成4??100米混合泳接力队?案例混合泳接力队的选拔甲乙丙丁戊蝶泳1’06”857”21’18”1’10”1’07”4仰泳1’15”61’06”1’07”81’14”21’11”蛙泳1’27”1’06”41’24”61’09”61’23”8自由泳58”653”59”457”21’02”45名候选人的百米成绩穷举法:组成接力队的方案共有5!=120种。

运筹学课件 cij(秒)~队员i 第j 种泳姿的百米成绩约束条件每人最多入选泳姿之一cij i=1 i=2 i=3 i=4 i=5 j=1 66.8 57.2 787067.4 j=2 75.6 6667.8 74.2 71j=3 8766.4 84.6 69.6 83.8 j=4 58.6 53 59.4 57.2 62.4 每种泳姿有且只有1人MMMMMj=5 11111运筹学课件模型求解最优解:成绩为253.2(秒)=4’13”2甲乙丙丁戊蝶泳1’06”8 57”2 1’18” 1’10” 1’07”4 仰泳1’15”6 1’06”1’07”8 1’14”2 1’11” 蛙泳1’27” 1’06”4 1’24”6 1’09”6 1’23”8 自由泳58”6 53” 59”4 57”2 1’02”4甲~ 自由泳、乙~ 蝶泳、丙~ 仰泳、丁~ 蛙泳.运筹学课件丁蛙泳c43 =69.6??75.2，戊自由泳c54=62.4 ?? 57.5, 方案是否调整, 敏感性分析,乙~ 蝶泳、丙~ 仰泳、丁~ 蛙泳、戊~ 自由泳最优解:x21 = x32 = x43 = x51 = 1, 成绩为4’17”7c43, c54 的新数据重新输入模型，再求解指派(Assignment)问题:每项任务有且只有一人承担，每人只能承担一项，效益不同，怎样分派使总效益最大. 讨论甲~ 自由泳、乙~ 蝶泳、丙~ 仰泳、丁~ 蛙泳.原方案运筹学课件某商业集团计划在市内四个点投资四个专业超市，考虑的商品有电器、服装、食品、家俱及计算机等5个类别(通过评估，家具超市不能放在第3个点，计算机超市不能放在第4个点，不同类别的商品投资到各点的年利润(万元)预测值见表5-36(该商业集团如何作出投资决策使年利润最大。

指派问题的应用 ,270260220计算机180 , 200 90 家具300 380 160 150 食品260 420 350 80 服装400 360 300 120 电器4321地点商品表5-36利润表运筹学课件【解】这是求最大值、人数与任务数不相等、不可接受的配置的一个综合指派问题，分别对表5-36进行转换((1)令c43=c54=0(2)转换成求最小值问题，令M,420，C`ij=M-cij，得到效率表(机会损失表),即转换后得到表5-37(3)虚拟一个地点5420150160200计算机240420220330家俱0 120 40 260 270 食品0 160 0 70 340 服装0 20 60 120 300 电器5 4 3 2 1地点商品表5-37 运筹学课件用匈牙利法求解得到最优解最优投资方案:地点1投资建设计算机超市，地点2投资建设服装超市，地点3投资建设食品超市，地点4投资建设电器超市，年利润总额预测值为1350万元7039018050140380406020100401001108010020110运筹学课件1(指派模型的特征2(匈牙利法求解指派问题的条件 3(匈牙利法的两个基本定理 4(指派问题也是一个特殊的运输问题.5(将指派(分配)问题的效率矩阵每行分别加上一个数后最优解不变.指派问题assignment problemThe End of Chapter 5作业:P135 T7 运筹学课件。